基于极化联合特征值的雷达弱小目标检测方法

王 威，杨 勇，韩静雯

（国防科技大学电子科学学院，湖南长沙 410073）

0 引 言

随着无人化作战装备的发展，无人机、无人艇等装备在现代战争中开始崭露头角［1-2］。在复杂多变的海杂波影响下，无人机、无人艇等具有较低雷达散射截面积的目标回波信号常常淹没在杂波背景中，在观测时间较短的情况下，脉冲积累数较少，造成雷达短脉冲积累下目标检测概率下降，给海面弱小目标的检测带来了严峻的挑战［3-4］。因此，为了提高海面弱小目标的检测能力，需要针对海杂波背景中短脉冲积累条件下雷达目标检测问题开展深入研究。

海杂波背景下的目标检测问题核心在于提高目标与杂波信号之间的差异，在恒定的虚警率下提高检测概率。恒虚警率（Constant False Alarm Rate,CFAR）技术的主要目的是在背景噪声较强的情况下，通过自适应地调整阈值来保持相对恒定的虚警概率［5］。CFAR检测主要从时域［6-7］、频域［8-9］和极化域［10-11］进行设计，但在雷达短脉冲积累条件下的检测性能不佳。针对雷达短脉冲积累下表现较好的方法有从信息几何角度设计的矩阵CFAR检测方法［12-13］和近些年提出的特征值CFAR 检测方法［14-15］。

特征值CFAR 检测方法在矩阵CFAR 检测方法的基础上作了改进，利用信号协方差矩阵的特征值运算代替复杂的矩阵运算。文献［14］利用信号协方差矩阵的最大特征值设计了基于最大特征值的检测算法（Maximum Eigenvalue-based Matrix CFAR Detector, MEMD），论证了所构建的检验统计量的恒虚警性质，并通过仿真和实测数据验证了其性能优于经典信息几何方法；文献［15］利用信号协方差矩阵的全部特征值，提出了三种新的特征值检测器：最大特征值-算数平均（Maximum eigenvalue to Arithmetic Mean,MAM）、最大特征值-几何平均（Maximum eigenvalue to Geometric Mean,MGM）、最大特征值-最小特征值（Maximum eigenvalue to Minimum Eigenvalue, MME），该三种检测器的优点是可以利用三参数Burr 分布从理论上推导出虚警概率、所选阈值和检测概率的解析表达式，但这三种方法仅在一组实测数据上进行了验证。此外，基于特征值的检测方法仅使用了单极化通道的数据，且在不同极化方式上的数据检测性能差异明显，鲁棒性不强，对于多极化体制的雷达并不适用，如何将极化信息引入特征值检测方法来提升检测性能值得研究。

为此，本文基于特征值检测方法，并结合全极化体制雷达的多极化通道数据，利用目标与杂波的极化相干矩阵的特征值信息差异，提出了一种基于极化联合特征值的雷达弱小目标检测方法。最后，通过对多组实测数据的验证，证实了所提方法的有效性。

1 雷达信号模型

不失一般性，雷达信号CFAR 检测问题可以表示为二元假设检验模型：

对于海面静止或慢动目标，各极化通道接收信号可以建模为

式中ahh,ahv,avh,avv表示各极化通道目标信号的复幅度，p为多普勒导向矢量，可以表示为［16］

式中，fd为目标信号的多普勒频率，fr为雷达脉冲重复频率，N为单个相干处理间隔中发射的脉冲数，上标T表示转置运算。

基于K 分布假设，海杂波c的幅度PDF 可以表示为［17］

式中，v和α分别为形状参数和尺度参数，Γ 是伽马函数，Kν-1是第二类v- 1阶修正贝塞尔函数。

2 基于极化联合特征值的检测方法

对于特征值检测方法，其仅针对单极化通道数据进行处理，若利用全极化通道数据，可能会提高检测性能。因此，下面提出了一种基于极化联合特征值的雷达弱小目标检测方法。

2.1 多极化通道联合处理

当满足互易性假设条件XHV=XVH时，可以计算得到极化相干矩阵［18］：

极化相干矩阵为3×3维半正定厄米特阵，具有非负实特征值λ1＞λ2＞λ3，可推导得出［18］

式中，极化相干矩阵的第二个特征值代表了HH、VV 的相干强度，最大特征值即为两同极化通道的总强度之和减去相干强度［18］。可将极化相干矩阵最大特征值作为多极化通道联合处理的输出，并基于此进一步计算联合特征值，多极化通道联合处理流程见图1。

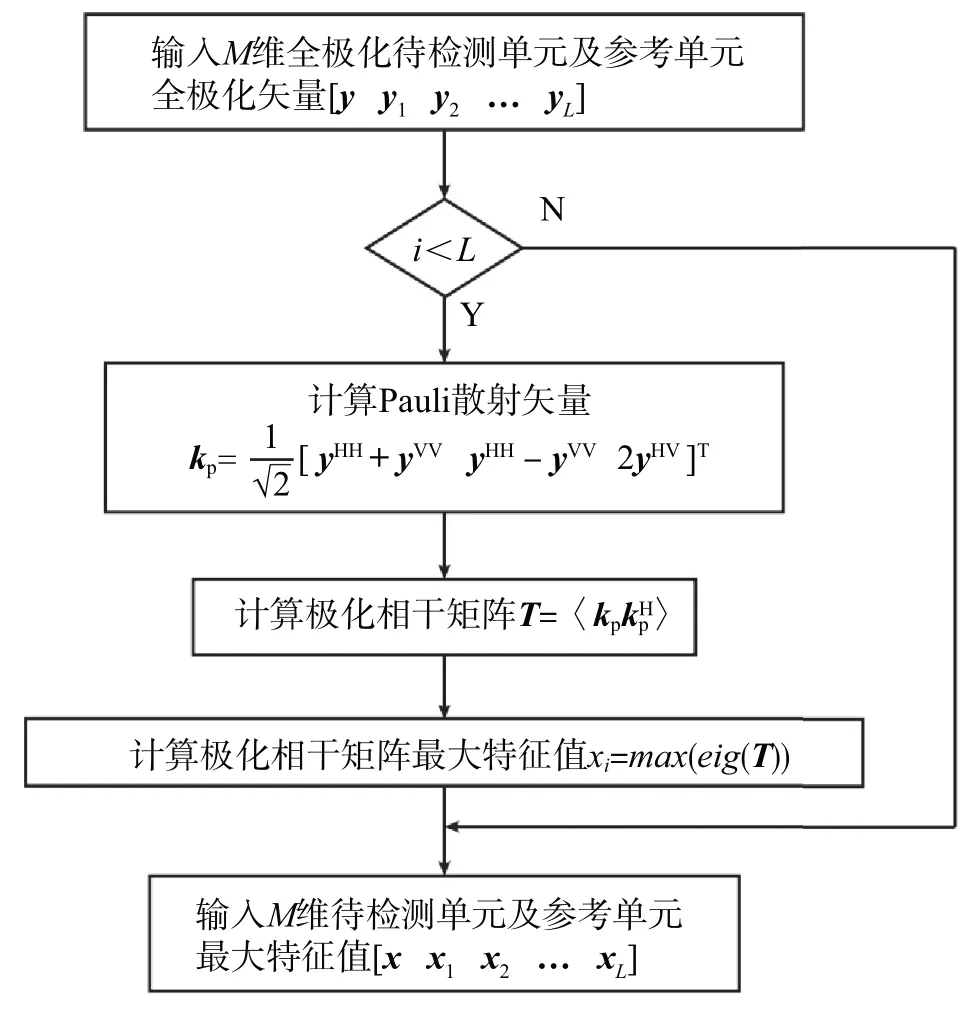
图1 多极化通道联合处理流程图

2.2 基于极化联合特征值的雷达弱小目标检测方法

下面介绍基于极化联合特征值的雷达弱小目标检测方法的具体步骤。

1）首先对待检测单元和参考单元接收到的回波数据进行多极化通道联合处理得到。

2）计算多极化通道联合处理后的数据构成的协方差矩阵{R,R1,R2,…,RL}。

协方差矩阵用R表示，x表示多极化通道联合处理得到的信号矢量，则协方差矩阵R可以由下式计算：

式中，rk表示相关系数，1，1 ≤i≤n，n为脉冲积累个数，上标表示取共轭。实际应用中，相关系数通常由时间平均代替统计平均计算：

3）分别求解待检测数据构成的协方差矩阵R的最大特征值λmax和参考单元接收到的数据构成的协方差矩阵{R1,R2,…,RL}的特征值组，每个特征值组λG={λ1,λ2,…,λk}包含对应协方差矩阵的全部特征值，k为协方差矩阵的秩。

4)分别计算特征值组的极大值λmax、极小值λmin、算数平均和几何平均。

基于极化联合特征值的检测方法判决式可写为

式中，η表示由虚警概率确定的判决门限，λmax,λmin,λmean,λave分别表示由特征值组计算得到的极大值、极小值、算数平均和几何平均。

基于极化联合特征值的雷达弱小目标检测方法原理图可用图2表示，其中算法选择模块表示根据不同的算法计算特征值组的极大值、极小值、算数平均和几何平均。

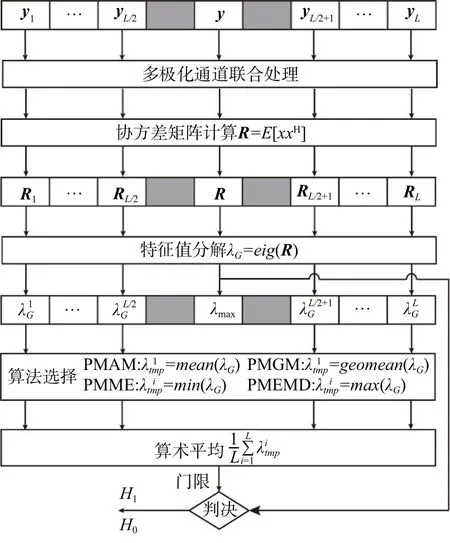
图2 基于极化联合特征值的雷达弱小目标检测方法原理框图

3 实验验证

本文使用了加拿大McMaster 大学提供的1998年IPIX 雷达（Ice Multi-parameter Imaging X-Band Radar）海杂波数据作为实测数据。雷达架设高度为20 m，雷达工作频率为9.3 GHz，波束宽度为0.9°，距离分辨率为30 m，脉冲重复频率为fr= 1 000 Hz，包含28 个距离单元。IPIX 雷达采用双发射∕接收极化，在进行数据采集时可以得到HH，HV，VH 和VV 4个极化通道的回波数据［19］。

选取第185 号文件进行分析，其中，第1～13 个距离单元为纯杂波数据，在第7个距离单元中加入了多普勒频率fd= 150 Hz 的全极化目标信号［20］。采用基于特征值的检测方法（MEMD、MAM、MGM、MME）和基于极化联合特征值的检测方法（PMEMD、PMAM、PMGM、PMME），并进行了比较。

图3 为上述方法的CFAR 归一化检验统计量，信噪比为6 dB。可以看出，基于极化联合特征值的检测方法相比基于特征值的检测方法的归一化检验统计量区分度有了一定的提升。

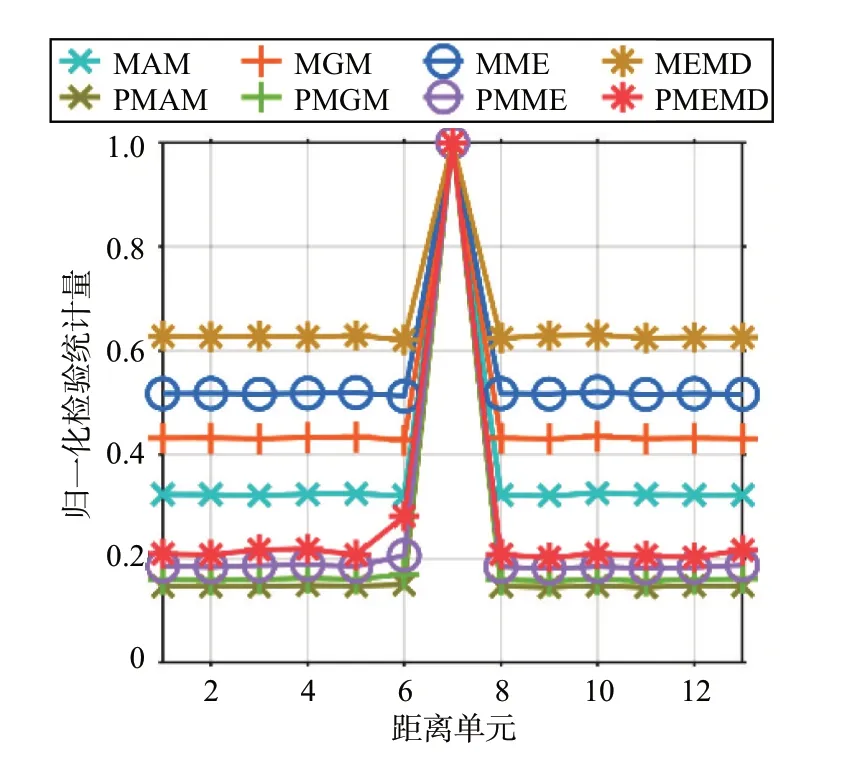
图3 CFAR归一化检验统计量

图4展示了原始数据、多极化通道联合处理后的数据以及使用SPAN检测器（Span Detector,SD）、功率最大综合检测器（Power Maximization Synthesis detector, PMS）和极化检测最优滤波器（Polarimetric Detection Optimization Filter, PDOF）的检测效果［11-12］，信噪比设置为6 dB。可以看出两种极化检测器在低信杂比条件下检测性能较弱。

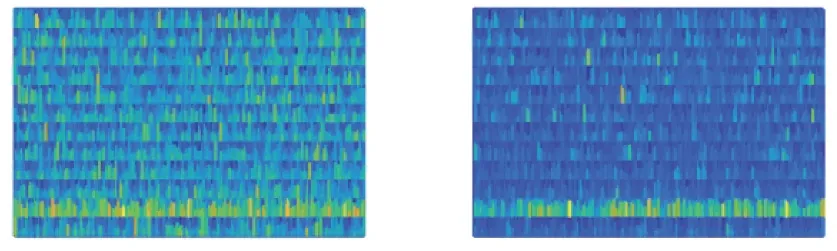
图4 实测数据检测效果

图5 绘制了基于极化联合特征值的检测方法（PMAM、PMGM、PMME、PMEMD）与极化检测方法（SPAN、PMS、PDOF）的检测性能曲线，信噪比设置为-5～15 dB。从结果可以看出，检测概率为0.8 时基于极化联合特征值的检测方法与三种极化检测方法性能相比提升1.5～5 dB。

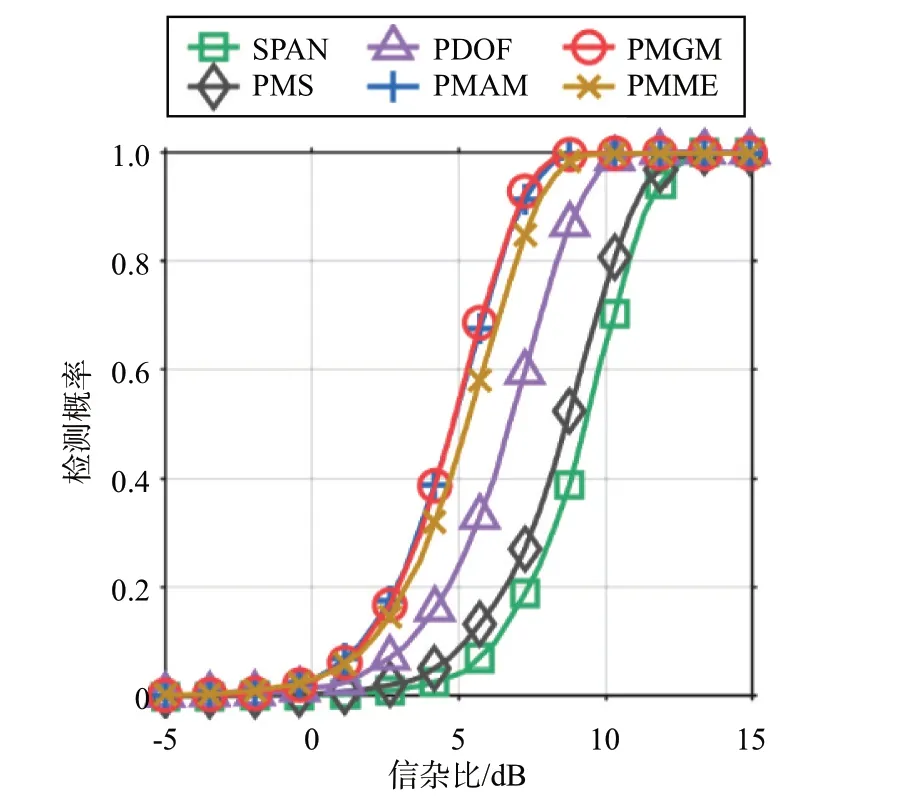
图5 实测数据检测性能曲线对比1

图6 对比了基于极化联合特征值的检测方法与基于特征值的检测方法的检测效果，信噪比设置为6 dB。可以看出，基于极化联合特征值的检测方法的检测性能相比基于特征值的检测方法检测性能有了一定的提高。

图6 实测数据检测效果对比

图7 绘制了基于特征值的检测方法（MAM、MGM、MME、MEMD）与基于极化联合特征值的检测方法（PMAM、PMGM、PMME、PMEMD）的检测性能曲线，信噪比设置为-5～15 dB。从结果可以看出，PMGM、PMME 与PMEMD 性能相近，检测概率为0.8时基于极化联合特征值的检测方法的检测性能与基于特征值的检测方法性能相比提升约2 dB。

图7 实测数据检测性能曲线对比2

为了验证所提算法稳健性，从1998 年IPIX 数据集中选取了另外10 组数据文件（167，169，170，171，172，173，174，176，177，183）进行测试，信噪比设置为6 dB。结果如图8 所示，上方4 条曲线代表了基于极化联合特征值的检测方法的检测概率。从图中可以看出，所提方法在检测效果上优于基于特征值的检测方法。

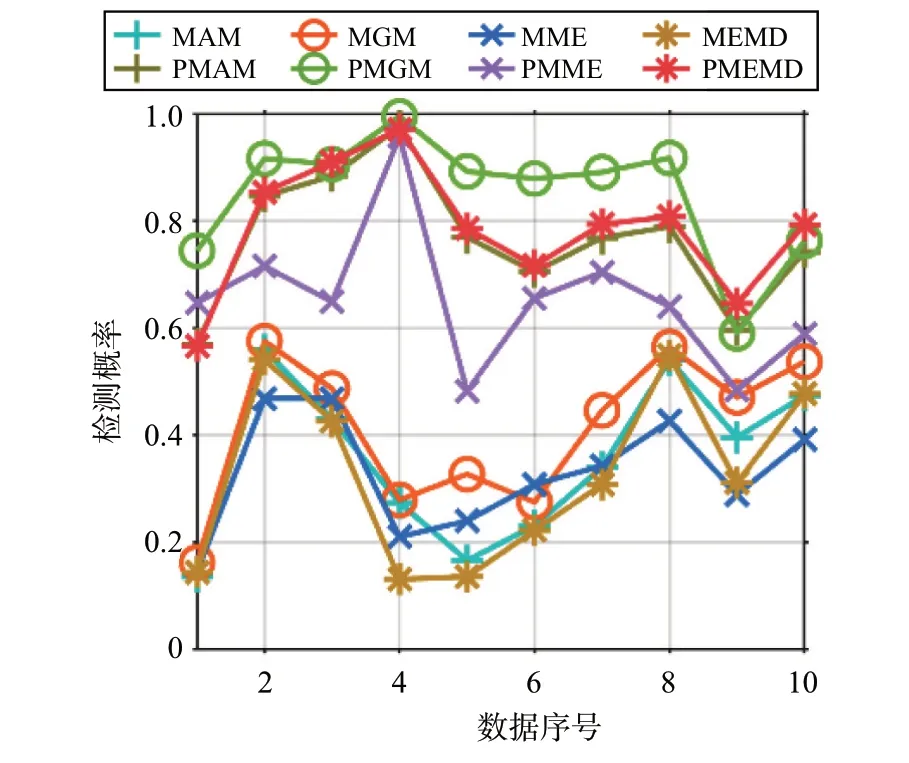
图8 各检测器的检测概率

4 结束语

本文提出了一种基于极化联合特征值的雷达弱小目标检测方法，该算法应用于多极化体制雷达检测中。本文通过实测数据对基于极化联合特征值的雷达弱小目标检测方法、基于特征值的检测方法和极化检测方法进行了性能比较。实验结果显示，基于极化联合特征值的雷达弱小目标检测方法优于基于特征值的检测方法2 dB，优于PDOF极化检测方法1.5 dB，优于SPAN、PMS方法5 dB。