省级统一命题背景下初中数学复习教学的思考与实践

2024-04-02王红权浙江省杭州市基础教育研究室

教学月刊（中学版） 2024年7期

王红权|浙江省杭州市基础教育研究室

初中学业水平考试省级统一命题需要依据义务教育课程标准，坚持素养导向、知识与能力并重的基本原则，以必备知识为载体，着重考查核心素养和关键能力.省级统一命题意味着评价标准的统一，即依标命题，这对教师和学生都提出了挑战.正如《中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见》中指出的那样，需要切实“引导教师深入理解学科特点、知识结构、思想方法”，进一步理解课程标准，理解“教—学—评”一致性的内涵.因此，当务之急是着力改变复习教学的基本模式，如“罗列知识点（美其名曰“画思维导图、知识结构图”）+分析题型套路+刷题”的模式等，使课堂教学从“教师中心”“知识中心”转变为“核心素养导向”，着力构建以提升能力、发展素养为锚点的数学复习课堂教学新范式.

一、梳理·运用：构建联系，提升能力

提升能力、内化素养，既是复习（本文所指的复习是学段末的综合复习）的途径，也是复习的目的.复习时，教师既要系统梳理知识，使学生“温故知新”，也要引导学生学会综合运用知识解决问题，做到“融会贯通”.也就是说，复习教学既要引导学生构建数学知识之间的联系，更要让学生透彻理解数学的本质.

（一）梳理的目的是建立知识之间的关联

当下复习课教学中流行的梳理，只停留在基础知识的罗列层级，常见的形式是知识列表、填空或思维导图等，虽也能呈现出一定的结构特征，但这种结构比较松散，追求的只是知识的覆盖.这种梳理方式只适用于章新课结束的复习，即在章新课结束时，教师引导学生通过梳理使所学知识结构化，明晰该章的学习重点和难点.而中考前总复习中的梳理，应该是梳理知识之间的关联以及它们是如何关联的.实际上，关联两个或多个不同知识的纽带，往往是它们最为核心的部分，因此通过梳理，既可以实现透彻理解数学本质的目的，也能使知识具有整体性和良好的结构.

情形一：在复习A 知识（知识群）时，建立知识A 与知识B 或者场景C 之间的联系.例如，特殊三角形与场景的关联有：（1）矩形的两条对角线把矩形分割成4个直角三角形和4个等腰三角形；（2）正方形的两条对角线把正方形分割成4 个等腰直角三角形；（3）菱形的两条对角线把菱形分割成4个等腰三角形和4个直角三角形；（4）垂径定理就是等腰三角形与圆（场景）结合的结果；等等.特殊三角形与知识的关联有：（1）与一般三角形的关联（如“投影”）；（2）与特殊三角形的关联（如“黄金比”）；等等.特殊三角形与场景和知识的关联如图1所示.

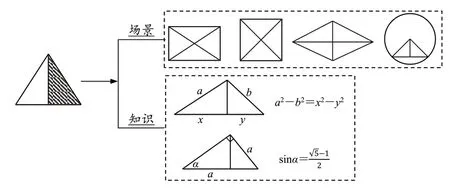
图1 特殊三角形与场景和知识的关联

通过场景关联，学生能熟悉知识A在场景B中的位置关系和数量关系（特殊性质），增加学习体验，积累学习经验，为未来解题提供熟悉的环境和有用的经验.通过知识关联，学生能更为深刻地理解对象的性质.如直角三角形与一般三角形的关联，其结果“a2－b2＝x2－y2”反映的是：通过投影的方法可以把一个二维结构“a2－b2”转化为一维结构“x2－y2”.因此，可以通过实数运算解决问题.

情形二：在复习A 知识（知识群）时，可以建立与A 相关的知识网络.透过知识网络，容易发现单元的重点和难点，从而凝练出统摄单元的一般观念.例如，梳理“方程”单元的知识结构（如图2所示）可知，统摄该单元的一般观念是消元和降幂思想.这个一般观念传递的是一种认知信念：不论是多元问题还是高次问题，都可以化归为“一元”或者“一次”的问题来解决.它也意味着一种行动指南：多元问题需要消元，高次问题需要降幂.同时，它又体现为一种知识系统：方程是按照一定的序（“元”和“次”）构建起来的一个有序结构.因此，它还蕴含着一种思维视野：从一元到多元、从一次到高次、从特殊到一般.由此，我们就可对一元二次方程的不同解法形成理性的价值判断：配方法的价值在于导出求根公式；求根公式为求解一元二次方程提供一般方法；而因式分解法则是一种解决问题的思想方法［1］.

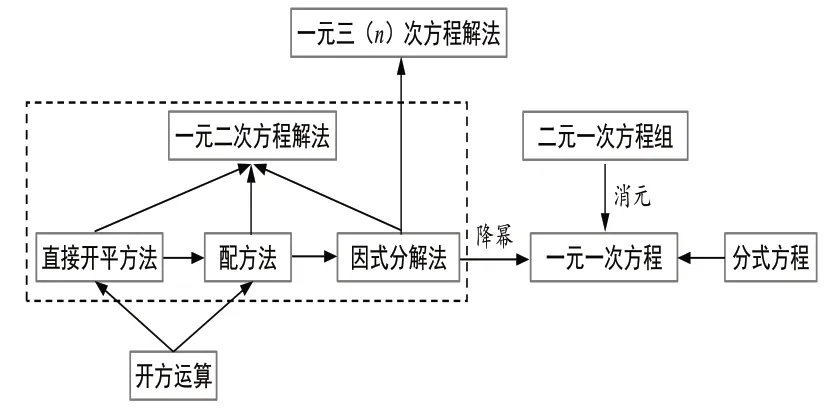
图2 “方程”单元的知识结构

情形三：在复习A 知识（知识群）时，关键在于建立知识A与场景B之间的联系.确立关联知识A 和场景B 的纽带是关键，也就是说，知识A 和场景B 之所以关联是需要有“牵线者”的.一般而言，这个“牵线者”一定是揭示知识A和场景B的最为核心的部分，譬如等腰三角形的“三线合一”和圆的“直径对直角”，有时候二者关联后“生成”的新的基本图形也至关重要.例如，课题“等腰三角形遇见圆”，关键在于等腰三角形是如何“遇见”圆的.也就是说，这个“牵线者”是谁、是如何“牵线”的等问题，是关联等腰三角形（知识）和圆（场景）的关键.如图3 所示，△ABC是等腰三角形（AB＝AC），由左侧虚线框中的图形可知：①中的辅助线AD就是关联等腰三角形和圆的纽带，它既是等腰三角形的“合一”三线，也是圆的“直径对直角”的直角边；②中由线段DE能生成新的等腰三角形EDC；③中角平分线AD和等腰三角形在场景内关联，形成充要条件“BD＝DC⇔∠BAD＝∠CAD”，事实上，还有更为深刻的结论“AB·AC＝AE·AD；BD2＝DE·DA”；等等.

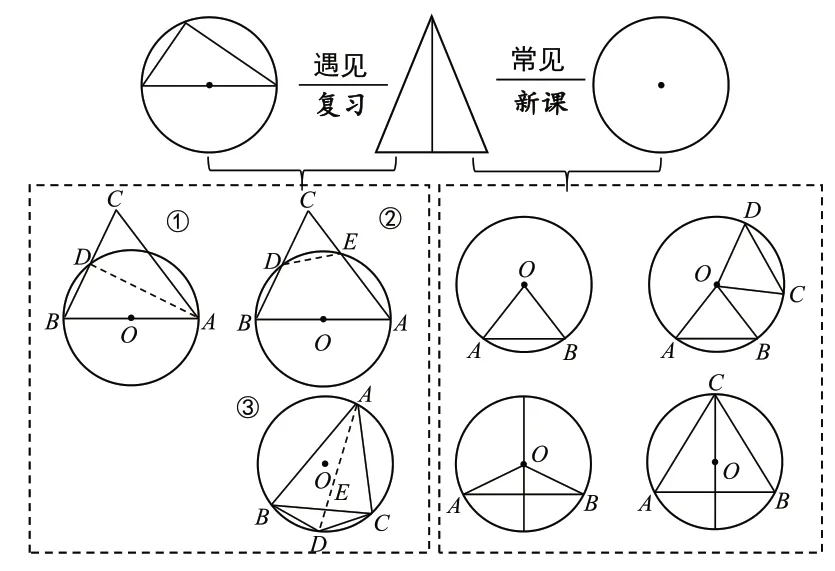
图3 “等腰三角形遇见圆”新课与复习课对比

情形四：对试题进行关联、统整和结构化研究.

题1：在△ABC中，AD⊥BC于点D，求证：AB2－AC2＝BD2－DC2.

题2：四边形ABDC的对角线AD⊥BC于点E，求证：AB2－AC2＝DB2－DC2.

题3：点P是矩形ABCD内一点，求证：PA2＋PC2＝PB2＋PD2.

题4：点D是等腰直角三角形ABC的斜边BC上一点，求证：BD2＋DC2＝2DA2.

题5：点D是等腰三角形ABC的底边BC上一点，求证：AB2－AD2＝BD·DC.

对这5 道题作分析，可以整理为如图4 所示的结构图，下面具体分析.把题1 作为一个基本结论，则题2 只要两次利用题1 结论（AB2－AC2＝BE2－EC2；BD2－DC2＝BE2－EC2）即可求证.

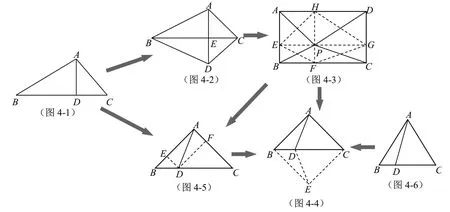
图4 各问题整合结构图

题3 只需要过点P作两条垂直于边的线段EG和FH，四边形EFGH满足题2的条件，因此EH2＋FG2＝EF2＋HG2.显然，EH＝PA，EF＝PB，FG＝PC，GH＝PD，所以题3得证.

题4 有三种证明方法：一是将等腰直角三角形ABC补全为正方形ABEC，则根据题3结论，有BD2＋DC2＝DA2＋DE2，显然，DE＝DA；二是受题3 启发，过点D作DE⊥AB于点E，DF⊥AC于点F，即图4-5 的方法，则BD2＋DC2＝2（DE2＋DF2）＝2DA2；三是将4-6 作为基本图形，由题5 的结论推出，因为AB2－AD2整理即得.

（二）运用的关键是在新场景中解决问题

复习的目的是提升学生综合解决问题的能力，表征为学习迁移.学习迁移是已经获得的知识和经验对解决其他问题所产生的影响，本质就是认知结构在新条件下的重新构建，旨在使学习者形成对知识的深刻理解.因此，复习教学需要关注知识和经验在不同应用场景中的迁移.也就是说，复习知识A 不能仅仅在A 场景中应用（这样做固然可以提升对知识A的熟练程度，但对提升学生解决问题的能力作用不大），而必须在场景B、场景C 等不同的场景中应用.学生如能在新的场景中用知识和经验解决问题，则说明其能力已经得到了提升.

例1［2］：在△ABC中（图略），AC＝BC，以AB为直径的⊙O分别交BC，AC于点D，E.求证：

显然，连接等腰三角形ABC和⊙O的纽带是线段AD，通过“三线合一”知AD平分∠BAC，因此本题的证明思路就非常清晰了.

例2：如图5 所示，已知△ABC∽△ADE，BD⊥BC.求证

图5

显然，在三角形中，关联结构CA2－CB2和EB2－ED2的纽带是三角形的高线.因此，分别作△ABC和△BDE的高线CG和EH，则CA2－CB2＝AG2－BG2，EB2－ED2＝BH2－DH2.

可以证明△ADB∽△AEC，所以∠ABD＝

所以∠BCE＝∠ACG，所以

例3：（2024 年1 月杭州市拱墅区期末卷）如图6 所示，四边形ABCD内接于⊙O，对角线AC平分∠BAD，连接BD交AC于点E.求证：AC2＝BC2＋AB·AD.

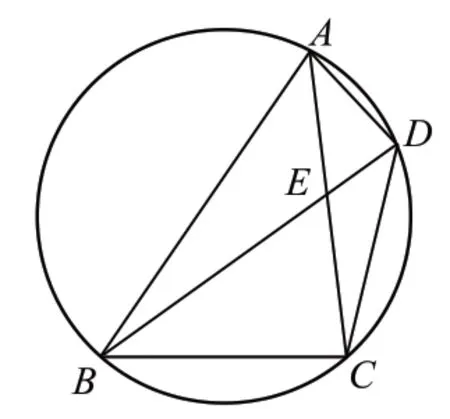
图6

证明：由图3-③的结论，知AB·AD＝AE·AC，BC2＝CE·CA.

因此AC2－AB·AD＝AC2－AE·AC＝CE·AC＝BC2.

所以AC2＝BC2＋AB·AD.

例4：（2024 年1 月杭州市西湖区期末卷）如图7所示，在△ABC中，AB＝AC，点P为线段BC上任意一点（P与B，C不重合），连接AP.若AB＝m，AP＝n，请用含m，n的代数式表示BP·PC，并说明理由.

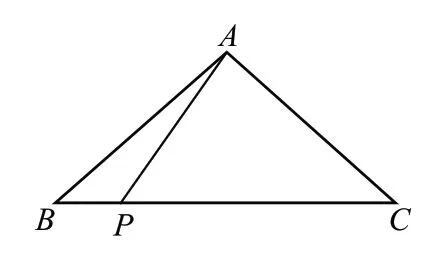
图7

解：由图4-5 的结论，知AB2－AP2＝BP·PC，即BP·PC＝m2－n2.

不难发现，有了知识间的联系分析，学生就能熟门熟路地解决问题.这样既能提高解题的准确率，也能缓解心理焦虑.

二、单元·整合：形成结构，发展素养

基于单元设计的复习教学，主要是指从模块入手，设计超越模块的任务，形成单元整体教学，帮助学生完善知识结构体系，实现核心素养的真正落地.因此，一般观念是单元整体教学的“魂”.单元整体教学的基本结构如图8所示.

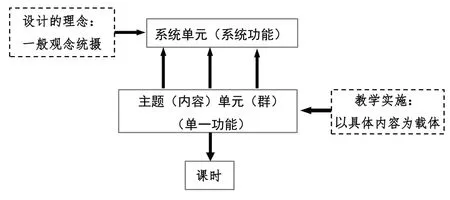
图8 单元整体教学的基本结构

例如“函数”单元复习教学设计，先要梳理出指导“函数”复习的一般观念，即需要梳理“函数”教学的内容逻辑和教学逻辑，具体如下.

其一，函数性质的研究.函数学习的核心是研究函数的性质，初等函数的性质一般包括单调性、对称性、最大（小）值和周期性等，但是对称性等性质都是由单调性的变化而引起的，如函数先增后减会形成最大值，周期性则是在不同的区间内重复同样的单调性，因此，研究函数的单调性是第一要务.研究函数单调性的数学工具是导数，但初中阶段未安排学习，因此需要创造直观工具.

其二，研究工具的创造.数学中有一种常用的方法就是把研究对象的未知空间通过映射，投影到已知空间中，然后在已知空间中研究清楚了，再进行逆映射，这样就能弄清楚这个未知空间对象的性质.函数是变量y的变化规律由变量x唯一决定的数学模型，即x和y总是成对出现，因此空间A中的元素可以用有序的数对（x，y）表示，而该有序数对的直观是平面直角坐标系的一个点，这样就可以把空间A中的有序数对（x，y）投影到空间B（平面直角坐标系）中，得到函数的图象，接下来就可以借助函数的图象研究函数的性质.

其三，图象的位置特征.在空间B 中借助平面直角坐标系的工具创造了研究函数性质的直观工具——函数的图象，这样，函数的图象就和直角坐标系发生了关系，其中最为重要的就是图象与坐标轴的关系.《义务教育数学课程标准（2022 年版）》对此的要求是“体会一次函数与二元一次方程的关系”“知道二次函数和一元二次方程之间的关系”，即函数与对应方程之间的关系，而连接二者关系的纽带就是函数的零点或者说是对应方程的根.

其四，一般观念的凝练.以函数的零点为纽带，统摄函数、方程和不等式的研究，是研究函数性质的一般观念，例5 是一个典型的试题.

例5：设函数y＝x2＋bx＋c（b，c是实数）.已知函数y的图象经过点（0，m）和点（1，n）两点（m，n是实数），设函数y＝x2＋bx＋c的图象与x轴交于（x1，0）和（x2，0）两点（0＜x1＜x2＜1），求证：0＜mn

解：设y＝（x－x1）（x－x2），

所以m＝x1x2，n＝（1－x1）（1－x2），

因为0＜x1＜x2＜1，所以

如此，通过二次函数的表达式y＝（x－x1）（x－x2），我们就可巧妙地将函数、方程和不等式连接起来.

其五，模型的应用价值.函数是刻画两个变量变化规律的数学模型，其目的是解决实际问题，其本质是在一般观念指导下的综合运用.

例6：已知一艘轮船上装有100吨货物，轮船到达目的地后开始卸货.设平均卸货速度为v（单位：吨/小时），卸完这批货物所需的时间为t（单位：小时）.

（1）求v关于t的函数表达式.

（2）若要求不超过5小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？

例6比较简单，此处不再分析.

其六，从结构图式到复习重点.由上述分析可以梳理出如图9 所示的“函数”单元结构图.从图中，我们可以发现复习教学的两条主线：主线1是函数（图象，性质）—位置特征（零点）—函数、方程和不等式；主线2 是函数（表达式，图象）—性质—应用.复习的重点应该聚焦函数、方程和不等式的综合及函数应用.

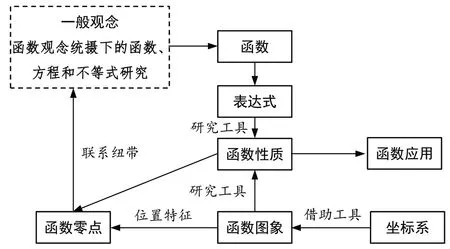
图9 “函数”单元结构图

三、作业·设计：厘清误区，提质增效

（一）厘清误区

在复习教学过程中，学生需要有一定量的训练，所以如何合理地设计训练系统至关重要.在设计作业的过程中，教师需要厘清以下三个误区.

误区1：不区分新授课作业和复习课作业的功能.新授课的教学目标主要是达成课标设定的目标，因此作业一般分为必做题和拓展题，其中必做题的主要功能是对目标的巩固和熟练，拓展题主要供学有余力的学生拓展学习视野，包括研究对象的历史赓续、文化自信、拓展推广等.复习课的作业可以分层，一般可以分为基础题和能力题：基础题用来巩固，属于必做题；能力题用来提高，可以作为选做题.

误区2：不区分自编作业和现成练习册的价值.教学调研表明，自编作业有一定的针对性和实时性，但常常不够系统、难度偏大.现成的练习册一般是考题的分类整理，选题有一定的代表性，但针对性和目标意识比较欠缺.因此，复习作业需要整合，以基础题促进知识的熟练，以能力题促进能力的提升.

误区3：不区分复习课训练系统和课后作业的差别.在“三位一体”复习课训练系统的构建中，前测、课堂检测和课后作业的协调、互补是作业设计的关键，要体现“教—学—评”一致性.前测决定复习教学的起点；课堂检测决定教学的节奏和方向；课后作业是课堂教学的延伸，起到巩固、评价（自评和他评）和提升能力的作用.