土壤空间变异对溶解性有机氮淋失风险影响的模拟研究

2024-04-01郝玉洁栾永霞郑西来郑天元

海洋湖沼通报 2024年1期

郝玉洁 ,栾永霞,郑西来, 3 * ,郑天元,能惠

(1.中国海洋大学环境科学与工程学院,山东青岛 266100;2.青岛市城阳区农业农村局,山东青岛 266109;3.中国海洋大学海洋环境与生态教育部重点实验室,山东青岛 266100)

引言

野外监测对于探究DON污染现状具有重要意义,但在大尺度下针对土壤特性进行逐一实验探究耗时费力,模型是进行相关研究的有力方式。Liang等[14]利用WHCNS_veg模拟了不同的农业管理方式下温室蔬菜系统中DON和硝态氮的迁移转化过程。Tian等[15]利用DRAINMOD-N II实现了景观生态系统中DON的运移过程的模拟。但这些模拟研究主要关注以点为尺度的均一土壤,未充分考虑土壤空间变异与DON淋失风险的关系,不利于做出合理的管理决策,因此有必要将土壤空间变异纳入DON淋失状况评估中。

灵敏性分析可以量化输入变量对模型输出的影响程度。其中,局部敏感性分析方法通过评估单个输入因子对模型的影响来进行参数的重要性排名。全局敏感性方法认为模型输出结果的改变是输入因子的改变以及不同因子之间相互交互作用的结果,扩展傅立叶幅度敏感性检验法(Extended Fourier Amplitude Sensitivity Test,EFAST) 作为一种基于方差分析的全局敏感词分析方法,能够量化每个参数对模型输出的无条件方差的贡献,已广泛应用于不同研究[16-17]。综合运用不同敏感性分析方法可以帮助我们识别影响DON淋失风险的关键性土壤特性。

本研究拟建立土壤DON迁移转化模型,探究水分渗漏和DON淋失对土壤初始状态和土壤水力学参数的空间变异的响应特征。同时,定量分析土壤空间变异对大尺度水分渗漏和DON淋失的影响,为评估DON淋失风险提供依据。

1 土壤水分-溶质运移模型构建

在模型中构建垂向高度为40 cm的均质土壤剖面。设置灌水定额为50 mm,灌溉强度为10 mm h-1,灌溉时间为5 h,假定水分在土壤表面均匀输入,故可将模拟情况简化为水分和溶解性有机氮(DON)在土壤剖面上的一维垂向运动。选择粪肥作为施加氮肥,施加量为 200 kg N ha-1,灌溉施肥过程设置为1/4W-1/2N-1/4W的模式[18]。考虑到灌溉施肥后水分及DON再分布过程中均有可能发生水分渗漏和DON的淋失,模拟时长设置为自灌溉开始96 h。

1.1 土壤水分运动模型

COMSOL中运用Richards方程来描述一维非饱和带水分运动,表达式为:

(1)

式中,h为土壤基质势,cm;z为垂向坐标,向上为正,cm;K(h)为非饱和导水率,cm d-1;运用van Genuchten模型描述水头特征曲线。

初始条件可以表示为:

h0=H-z,-40≤z≤0 cm,t=0

(2)

式中,h0为土壤初始总水势,cm;H为基质势,cm。

模拟区域上边界设定为大气边界,大气边界的水流量取决于土壤入渗量,下边界设定为自由排水边界,边界条件可以表示为:

(3)

(4)

式中,E(t)表示土壤表面入渗量,cm·d-1。

1.2 土壤DON迁移转化模型

COMSOL中运用对流弥散方程描述非饱和带溶质的迁移转化过程。DON随水分向下迁移的过程中经历的反应包括土壤释放DON以及DON的矿化和吸附。因此,DON在土壤中的运移过程可以表示为:

(5)

式中,c为土壤溶液中DON的浓度,mg N cm-3;s为吸附在土壤颗粒上的DON的含量,mg N kg1;ρ为土壤密度,g cm-3;t为时间,d;q为土壤水通量,cm d-1;D为水动力弥散系数,cm2d-1;μw,1和μs,1指液相中和固相中DON的矿化速率常数,d-1;μw,2和μs,2指液相中和固相中DON从土壤中的释放速率常数,d-1。

DON从土壤中的释放这一过程的模拟借鉴了DAISY模型中有机质周转过程的设置[19],DAISY模型指出,DON的形成是土壤有机质和微生物共同作用的结果,DON的释放速率可以表示为:

μw,2=μs,2=fDON(DSMB1+DSMB2+kSOM2)

(6)

式中,SMB指土壤微生物库;SOM指土壤有机质库,每个主库可以划分为两个部分:快速分解的库(SMB1和SMB2)和缓慢分解的库(SOM1和SOM2)。DOM指溶解性有机质库;fDON指从DOM到DON的分配系数;D指微生物死亡速率常数,d-1;k指分解速率常数,d-1,需要根据实际的黏粒含量,温度和体积含水量来进行修正,校准系数分别为0.7、0.9和1。

DON的吸附可以用Freundlich吸附模型来描述[20-21]:

s=KFcN

(7)

式中,KF指Freundlich模型中吸附常数,mg1-NL-Nkg-1;N为吸附线性指数,L mg-1。

假设土壤DON的初始浓度呈线性分布(以大沽河流域2019年部分区域氮素含量为参考[22],设置土壤剖面底层DON累积量较多,此时剖面底部DON淋失量较大),设置变化速率为0.000 5,土壤剖面上不同深度处土壤溶液中DON的初始浓度可以表示为:

c(z,0)=c0-0.0005×(40+z), -40≤z≤0 cm,t=0

(8)

式中,c0为土壤溶液中DON的初始浓度(z = -40 cm),mg N cm-3;

模拟区域上边界允许溶质输入,输入量取决于施肥强度,下边界为自由排泄边界,边界条件可以表示为:

(9)

(10)

式中,ca为肥料溶液中DON的浓度,mg N cm-3。

1.3 模型参数

1.3.1 土壤水力学参数

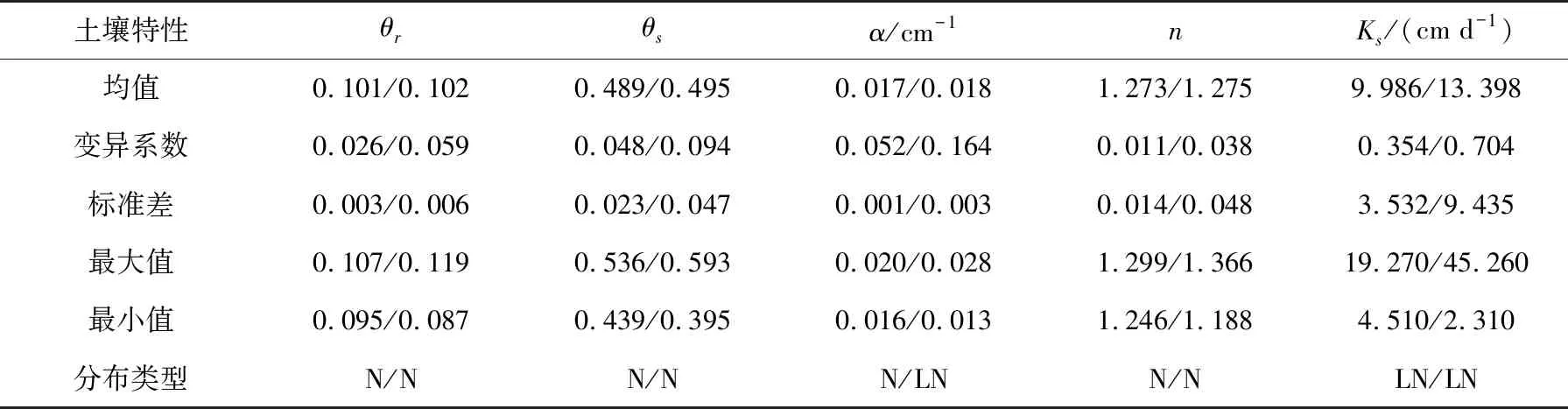
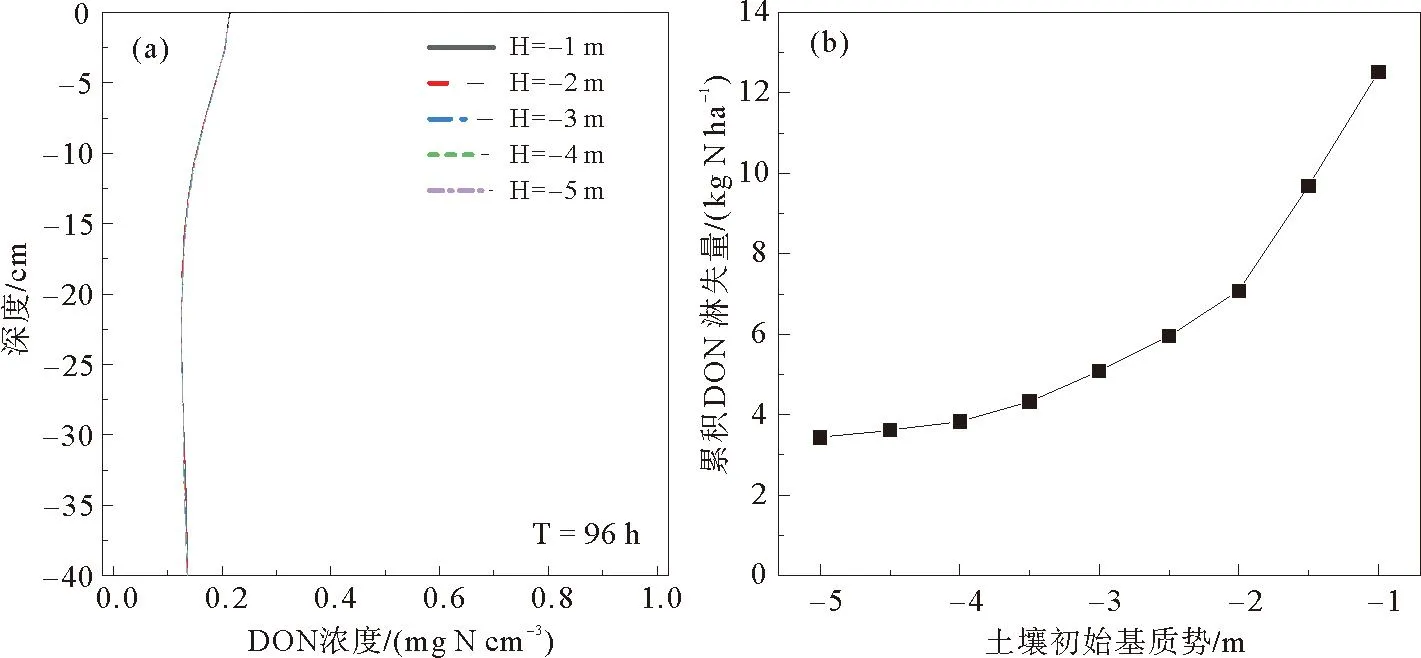
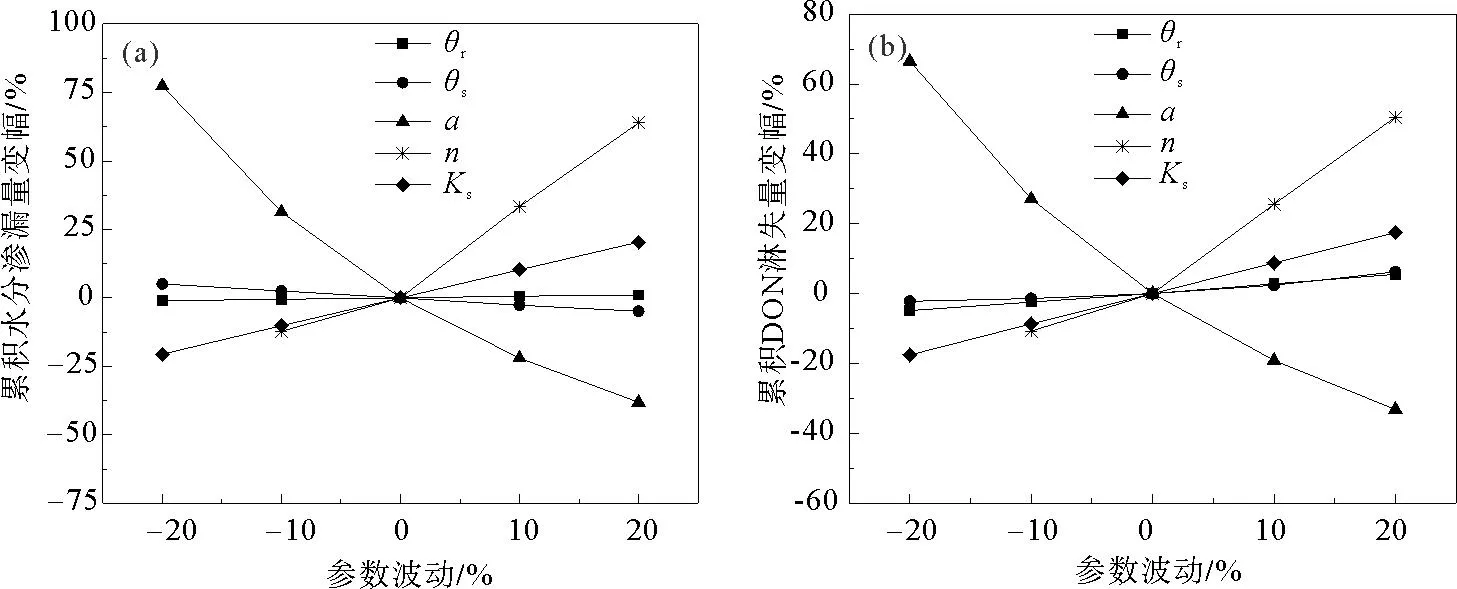
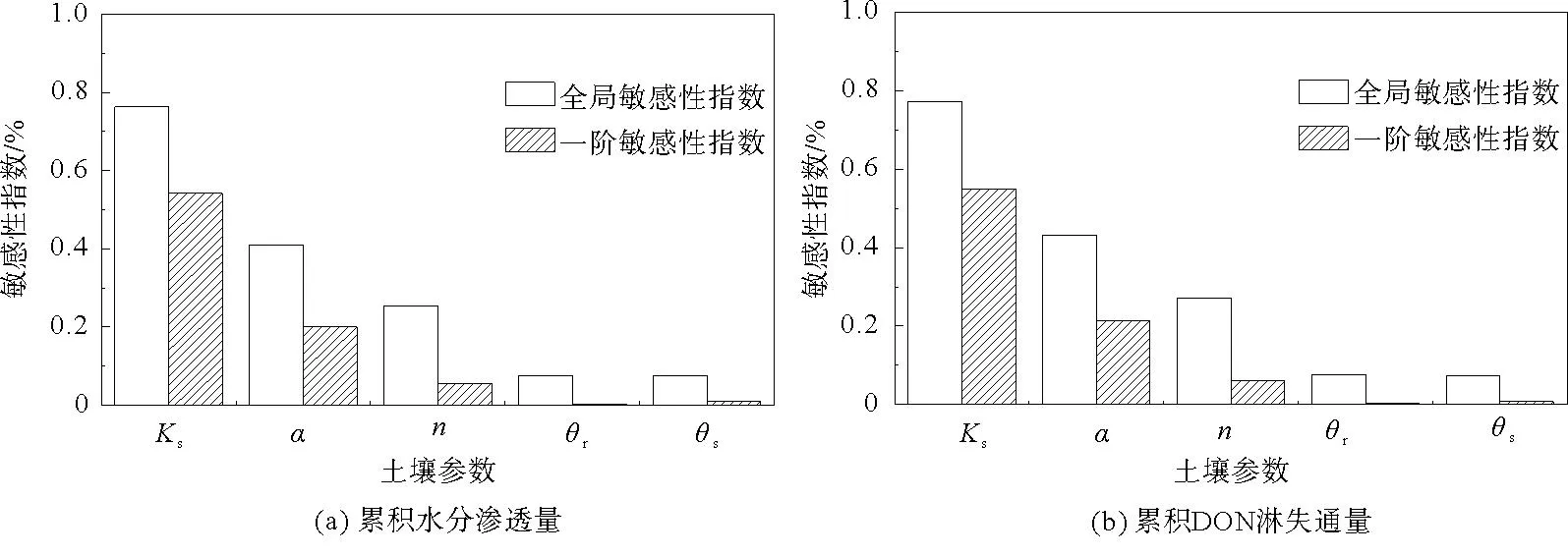
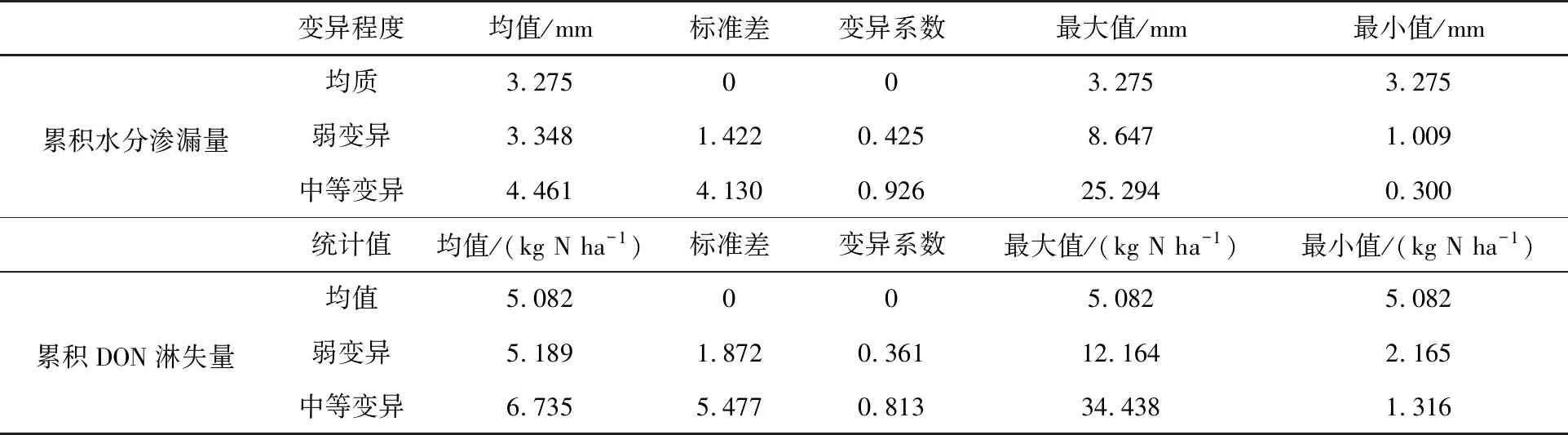
土壤水分特征曲线的模拟运用了van Genuchten模型,这个模型中包含5个独立的水力学参数:θr,土壤残余体积含水率;θs,土壤饱和体积含水率;α和n为经验拟合参数;Ks为饱和导水率,L T-1,利用Rosetta人工神经网络可以求得不同颗粒组成和容重土壤的水力学参数。为了探究土壤空间变异对土壤水分渗漏和DON淋失情况的影响,设定变异系数CV<0.1为弱变异、0.1

表1 不同变异程度土壤物理性质统计特征值

表2 不同变异程度土壤水力学参数统计特征值

1.3.2 溶质运移参数

纵向弥散系数取为DL=10 cm,DON在自由水中的分子扩散系数取为D=1.2 cm2d-1[14]。DON的矿化速率为μw,1=μs,1=0.02 d-1[14]。DON从土壤中的释放过程涉及到的相关参数设置如下:DSMB1=1.85×10-4d-1,DSMB2=0.02 d-1,kSOM2=1.40×10-4d-1[19]。以大沽河流域土壤为研究对象,该区域非饱和带土壤溶液碳氮比为26.3:2.79[22],假定在整个模拟过程中土壤溶液的碳氮比是恒定不变的,根据从DOM到DOC的分配系数(fDOC=0.05)和碳氮比计算可以得到从DOM到DON的分配系数值[19]。Freundlich吸附模型参数取值为KF= 2.619,N=1.788[21]。

1.4 敏感性分析方案

1.4.1 局部敏感性分析

探究不同初始浓度(c0取值为0.08、0.16、0.24、0.32、0.40 mg N cm-3)和初始基质势(H取值为-1、-2、-3、-4、-5 m)下土壤累积水分渗漏量和累积DON淋失量的影响,其它参数取均值,将待分析参数值输入COMSOL软件进行模拟。

探究不同土壤水力学参数对累积水分渗漏量和累积DON 淋失量的影响,其它变量取固定值(c0取值为0.16 mg N cm-3,H取值为-3 m),待分析参数波动值为±10%、±20%,将待分析参数值输入COMSOL软件进行模拟,与均值参数组模拟结果进行对照。

1.4.2 全局敏感性分析

扩展傅立叶幅度敏感性检验法(EFAST)结合了Sobol’法和傅立叶幅度敏感性检验法(FAST)的优点,是一种基于方差分解的全局敏感性分析方法。它的基本思想如下:

模型的总方差可以分解为:

(11)

式中,V表示模型总方差;Vi表示xi的自身波动引发的方差;Vij表示xi通过xj作用贡献的方差;Vijm表示xi通过xj、xm作用贡献的方差;V12…k表示xi通过其余k-1个变量作用贡献的方差。

变量xi的一阶敏感性指数表示xi对模型输出总方差的直接贡献率,可以表示为:

(12)

变量xi的全局敏感性指数表示xi对模型输出总方差的直接贡献率和变量之间的相互作用对模型输出总方差的贡献率之和,可以表示为:

(13)

式中,-i表示除变量xi之外的其它参数,V-i表示不包括xi的其它变量的波动引发的方差之和。

利用蒙特卡洛法对5个土壤水力学参数进行随机采样,每种变异程度采样445次(EFAST法认为有效采样次数需要大于参数个数×65),将待分析参数值输入COMSOL软件进行求解,利用MATLAB调动COMSOL软件进行模拟大批量的模拟,利用EFAST方法对模拟结果进行分析。

2 结果与分析

2.1 初始状态的影响

设置不同初始浓度(c0取值为0.08～0.40 mg N cm-3)和初始基质势(H取值为-1～-5 m)值,对水力学参数取均值,得到不同条件下土壤剖面上DON分布、含水率分布(T=96 h)情况以及底部累积水分渗漏量、累积DON淋失量(图1)。由于c0仅与土壤剖面上DON浓度分布和底部淋失通量有关,所以没有分析c0与土壤剖面上含水率分布和底部水分渗漏量的关系。

图1 不同初始DON浓度(c0)条件下土壤剖面上DON浓度分布和底部累积DON淋失量

如图1所示,当T=96 h时,DON浓度在整个剖面上呈下降趋势,大部分DON累积在土壤表层,0～10 cm土壤层中DON含量占整个剖面总量的32.70%～50.51%。随着c0的增加,土壤剖面各个深度的DON浓度都明显增大,累积DON淋失量也显著增加,说明土壤中存储的DON是DON淋失的重要来源。由图2可知,H对土壤剖面上体积含水率以及累积土壤水分渗漏影响较小。当T=96 h时,土壤体积含水率随深度的下降而降低。随着H的增加,土壤剖面上各个深度含水率小幅增加,土壤累积水分渗漏量随之增加。由图3可知,对于不同的H值,土壤剖面上各个深度DON含量没有明显差异,但是累积DON淋失通量随H的增加而增加。这是因为土壤基质势较高时,土壤易发生水分渗漏和溶质淋失[24],DON随水分大量淋失,土壤含水量降低,但是土壤中DON总量也降低,所以土壤剖面上DON浓度大小没有明显变化。

图2 不同土壤初始基质势条件下土壤剖面上含水率分布和底部累积水分渗漏量

图3 不同土壤初始基质势条件下土壤剖面上DON浓度分布和底部累积DON淋失量

2.2 土壤水力学参数的影响

2.2.1 局部敏感性分析

对五个土壤水力学参数(θr,θs,α,n,Ks)进行局部敏感性分析,参数波动值为±10%、±20%,将其它变量取固定值(c0取值为0.16 mg N cm-3,H取值为-3 m),可以得到不同条件下土壤累积水分渗漏量和累积DON淋失量,与均值参数组模拟结果进行对比,可以得到单个土壤水力学参数值发生波动时土壤累积水分渗漏量和累积DON淋失量的变化幅度(图4)。为了规避不合理的模拟结果,忽略当n<1.1的情形[25]。

图4 土壤水力学参数波动与累积水分渗漏量和累积DON淋失量变幅的关系

由图4(a)可知,五个水力学参数对土壤累积水分渗漏量影响程度从大到小依次为:α>n>Ks>θs>θr,其中n、α、Ks的影响较为明显,θr与水分渗漏过程量大小无明显关系。此外,累积水分渗漏量与n、Ks呈正相关,与α、θs呈负相关。随着α的增加,累积水分渗漏量显著下降,原因是α与土壤进气吸力是倒数关系,α的增加说明土壤进气吸力变小,土壤导水能力减弱[26],进而降低了土壤水分向深层的渗漏。随着n的增加,累积水分渗漏量下降,这是因为n值与土壤介质中孔隙分布有关,随着n值的增加,土壤孔隙中细小孔隙数量变少,土壤粘滞力降低,土壤导水能力增强[27]。随着Ks的增加,累积水分渗漏量呈线性增大的趋势。由图4(b)可知,五个水力学参数对累积DON淋失量影响程度从大到小依次为:α>n>Ks>θs>θr,与对累积土壤水分渗漏量的影响程度排名相同,且参数波动造成的累积土壤水分渗漏量和累积DON淋失量的变化幅度也基本一致,说明大量水分的渗漏可能伴随着大量DON的淋失,累积DON淋失量对土壤水力学参数中n、α、Ks的波动更为敏感。

2.2.2 全局敏感性分析

利用蒙特卡洛法对5个土壤水力学参数进行随机采样,每种变异程度产生445个模拟案例,将其它变量取固定值(c0取值为0.16 mg N cm-3,H取值为-3 m),可以得到不同条件下土壤累积水分渗漏量和累积DON淋失量,利用EFAST方法对模拟结果进行分析,计算得到五个土壤参数对两者的敏感性指数(图5、6)。如图5,6所示,五个水力学参数对累积水分渗漏量和DON累积淋失量的影响程度排序与局部敏感性分析结果不同,是因为土壤颗粒组成的变化对五个参数值的影响程度不同,即对于某一区域,五个水力学参数的变异程度是不一致的(表1、2),对水力学参数设定相同的变幅进行局部敏感性分析与实际情况会有偏差, 所以有必要首先确定五个参数值的取值范围和分布类型,得到符合实际分布的参数序列,进而进行敏感性分析得到的结果更为准确。

由图5(a)可知,土壤在弱变异条件下,五个水力学参数对累积土壤水分渗漏量影响程度依次为:θs>Ks>α>n>θr,由图1可知,θs和Ks对土壤累积水分渗漏量的影响最明显,对累积水分渗漏量的变化的方差贡献分别达到82.20%和82.13%,这是因为θs与土壤剖面可能存储的水分总量密切相关,θs较大时,同一体积含水率相应的负压值升高,土壤渗透性降低,水分易滞留在土壤孔隙中[26]。Ks与水分在剖面上的运移速度密切相关,Ks的空间变异程度(CV=0.354)明显大于其它参数,是造成土壤水分渗漏量不确定性的主要参数之一。由图5(b)可知,五个水力学参数对累积DON淋失量影响程度依次为Ks>α>n>θr>θs,Ks对累积DON淋失量全局敏感性指数为0.83(即可解释累积DON淋失量变化方差的83.00%),对DON淋失有较大影响。一阶敏感性指数的差异说明Ks、α的影响主要通过与其它参数的交互实现,而n、θr、θs的影响主要是直接作用引起的。

由图6(a)可知,五个水力学参数对中等变异土壤累积水分渗漏量影响程度与弱变异条件下顺序明显不同,五个水力学参数对累积土壤水分渗漏量影响程度依次为:Ks>α>n>θr>θs,Ks的全局敏感性指数为0.76,对土壤累积水分渗漏量影响程度最大,α和n对累积土壤水分渗漏量影响也较为明显。θs的全局敏感性指数为0.08,影响程度大幅度降低。由图6(b)可知,五个水力学参数对累积DON淋失量影响程度依次为Ks>α>n>θr>θs,累积DON淋失量的变化主要由Ks和α造成。由表2可知,中等变异粘土Ks的空间变异程度(CV=0.704)明显大于其它参数,这加剧了其对土壤水分渗漏量和DON淋失量不确定性的影响。

图6 中等变异土壤参数对土壤累积水分渗漏量和DON累积淋失量的全局和一阶敏感性指数

2.3 不同变异程度下区域土壤水分渗漏和DON淋失量

利用蒙特卡洛法对5个土壤水力学参数进行随机采样,每种变异程度产生445个模拟案例,将其它变量取均值(c0取值为0.16 mg N cm-3,H取值为-3 m),可以得到不同条件下累积DON淋失量和土壤水分渗漏量,将445个案例进行排列组合,可用于分析大尺度下地区土壤水氮淋失情况。由表3可知,两种变异程度下得到的累积水分渗漏量和累积DON淋失量变异系数都达到了中等变异程度(0.1

表3 不同变异程度累积土壤水分渗漏量和DON累积淋失量统计特征值

图7、图8给出了土壤在弱变异和中等变异条件下累积水分渗漏量和累积DON淋失量的频数直方图,纵坐标表示该区间的模拟值的数量占比,对频数直方图进行拟合,可以看出,累积水分渗漏量和累积DON淋失量出现的频率基本服从对数正态分布,拟合的得到的相关参数如表4所示。由图7、图8可知,在弱变异条件下,累积土壤水分渗漏量和累积DON淋失量范围是1.009～8.647 mm和2.165～12.164 kg N ha-1,在中等变异条件下,两者范围是0.300～25.294 mm和1.316～34.438 kg N ha-1,随着变异程度的升高,两者的变化范围都明显增大。对于大尺度地区,土壤空间变异性越大,土壤参数空间分布不均匀性增大,出现大规模水氮淋失的可能性越大。