潮汐流对珊瑚礁海岸波浪传播变形和非线性特性影响的试验研究

旷 敏,姚 宇,2*,邱祎辰,杨笑笑,蒋昌波,2

(1. 长沙理工大学 水利工程学院,湖南 长沙 410114;2. 水沙科学与水灾害防治湖南省重点试验室,湖南 长沙 410114)

引 言

珊瑚礁是由碳酸钙组成的珊瑚虫的骨骼在数百年至数千年的生长过程中形成的生物平台,主要分布于热带及亚热带地区[1],我国南海等地也蕴藏着非常丰富的珊瑚礁资源。已有研究表明,波浪作用是影响珊瑚礁水动力过程最重要的影响因素[2]。也有学者对全球珊瑚礁海域附近的波浪和潮汐条件进行调查,全球约三分之一的珊瑚礁海域水动力特性由潮流主导[3]。通常,珊瑚礁海域的水动力过程是波浪与潮汐流共同作用的结果。波浪从远海向珊瑚礁海岸传播中,首先在礁前发生浅化变形,随后在礁缘附近发生破碎并消耗大量能量,波浪破碎形成的增水会在礁坪上驱动向岸的波生流[4],波生流是礁坪上营养物质和珊瑚砂输运的重要载体。当潮差较大时,潮汐流可能会代替波生流成为礁坪上最重要的动力因子。同时,波浪在与珊瑚礁体相互作用过程中,波形会表现出明显的非线性特征,这些特征也会对礁坪上的营养物质和珊瑚砂的输运造成影响[5]。因此,研究潮汐流影响下珊瑚礁上波浪运动过程和非线性特性对于整个珊瑚礁海域生态环境保护和探讨岸滩演变规律具有一定的指导意义。

近十几年来,国内外学者主要采用现场观测、数值模拟及物理模型试验等方法研究波浪在珊瑚礁上的运动过程及非线性特征。Cheriton等[6]通过现场观测研究了珊瑚礁上低频长波的不对称度参数、偏度参数及厄塞尔数的变化规律,陈洪洲等[5]利用基于Boussinesq方程的FUNWAVE2.0数值模型模拟了不规则波在岸礁上的传播变形,分析了礁前斜坡坡度和礁面粗糙度对波浪非线性参数(不对称度和偏度)的影响;杨笑笑等[7]通过物理模型试验研究了大糙率下珊瑚礁附近规则波的非线性特性,并提出采用深水厄塞尔数来预测礁坪上非线性特征参数的经验公式。但上述研究尚未试验涉及潮汐流的影响。文献中,仅Yao等[8]通过物理模型试验研究了潮汐流影响下波浪破碎及增水特性,并提出了波浪增水的理论模型;随后Yao等[9]通过水槽试验研究了波浪在珊瑚礁上的传播变形,重点探讨了平均水位的沿礁变化。但Yao等的上述研究未考虑粗糙礁面和潮汐流对波浪的非线性特性的影响。

基于上述文献综述,本研究参考Yao等[10]使用圆柱体矩形阵列来模拟礁面粗糙度并结合YAO等[8]利用造流泵在水槽两端产生正反向流来模拟潮流涨潮与落潮过程的方法,拟通过物理模型试验对潮汐流影响下珊瑚礁海岸波浪传播变形及非线性特性进行研究。

1 物理模型试验设置

本试验在长沙理工大学水利实验中心波流水槽(长40 m,宽0.5 m,高0.8 m)中进行。如图1所示,水槽左端通过一台活塞式造波机来产生设计波况。参照Hench等[11]对法属波利尼西亚莫雷阿岛Moorea礁开展的原型观测数据(其礁坪水深为1～5 m,波高为0.85～2.60 m,周期为8～22 s,潮流流速为0.37～1.26 m/s),珊瑚礁物理模型按照弗劳德相似准则以1∶20的几何比尺和1∶4.5的时间比尺建造,试验采用19根电容式浪高仪(G1～G19)来测量沿礁波幅的变化: G1和G2设置在外海侧用来测量分离入射波和反射波,G3～G7均匀布置于礁前斜坡上,G8～G18布置于礁坪区域,由于波浪在礁缘附近运动较为剧烈,因此在礁缘的波浪破碎带附近所布置的浪高仪较为密集,G19设置在瀉湖中间。浪高仪具体的布置方式和各浪高仪间的间距如图1a所示。浪高仪的测量时长设为造波机启动后连续10 min,采样频率为50 Hz。

图1 (a)试验布置图;(b)珊瑚礁模型;(c)粗糙礁面;(d)糙率单元排列方式

如图1b所示,本试验中整个珊瑚礁礁面由0.01 m厚的PVC板分段拼接而成。礁前斜坡坡度为1∶6,坡角距造波机20.75 m,坡后接8 m的水平礁坪,礁坪面距槽底的高度为0.35 m,礁坪末端通过另一个斜坡与水槽底部相连接,水槽右端设有坡度为1∶8的礁后岸滩,因此在礁坪与礁后岸滩之间底宽为3 m的区域形成“潟湖”。为更加真实得模拟波浪在珊瑚礁面上的传播过程,本试验拟参考Yao 等(2018)的方法来模拟生长有鹿角类珊瑚的粗糙礁面,即拟在整个礁前斜坡至礁后岸滩坡脚区域上均匀布置由小木条制作的圆柱体,该圆柱体单元直径1 cm,高3.5 cm,露出礁面2.5 cm,圆柱体阵列等距排列,相邻柱间距为2.5 cm,如图1c所示。柱体的密度采用固体体积分数φ=VS/V计算,式中V为控制体体积,VS为控制体中圆柱体所占体积,由此可得φ=0.126,如图1d所示。本试验采用直径为240 mm的圆形管道连接瀉湖底部和造波机附近的槽底,管道中部设有变频造流泵和电磁流量计,可通过在管道和水槽系统中产生不同方向的循环流来实现对礁坪上潮汐流的模拟。

2 结果分析

2.1 波面时间序列的沿礁变化

图2展示了测试波况下无流、正向流和反向流存在时,规则波在外海(G1)、礁前斜坡(G5)、礁缘(G7)、礁坪前部(G11),礁坪中部(G14)和礁坪末端(G18)各有代表性的位置处波面的时间序列。

图2 H0=0.14 m,T=1.5 s,hr=0.10 m工况下沿礁有代表性的位置(G1、G5、G7、G10、G14 和 G18)波面的时间序列(η)

本试验截取540 s至570 s波面稳定的时间段进行分析,图2结果表明,在远海位置G1处,波面主要表现为波谷较宽且波峰较窄的斯托克斯波。当波浪传播至G5时,波浪在礁前斜坡发生浅化变形,使得波峰变窄变陡,波谷变得更平坦。在G7礁缘位置,波浪发生破碎,表现出典型的破碎波特征,波面出现明显的锯齿状。在礁坪上G10附近的破碎带内,此时波幅明显减小,波浪衰减显著。在破碎带末端G14处,波浪破碎已全部完成,礁坪上重新生成了透射波并且波面出现了次峰值,这是由于波浪与珊瑚礁地形相互作用产生了高频波成分所致(见2.4节)。G18位置与G14位置的波面形状几乎一致,但由于礁面大糙率的摩擦损耗,波幅进一步减小。

当波浪与潮流共同存在时,对比不同流向发现,正向(反向)流可以降低(增加)波高,同时增加(降低)波速和波长,造成了时间序列出现向前(向后)的相位差,同时也降低(增加)了波浪的非线性。这是因为波浪在有流的条件下传播时,色散关系会发生变化,即出现多普勒频移效应[12]。在礁坪上G10附近,正向流影响下波幅最大,这是由于流的存在改变了波浪的破碎发生的位置,正向流造成波浪的破碎向礁后岸滩方向移动(详见2.2节),因此能量耗散滞后。

2.2 波高和平均水位的沿礁变化

图3对比了在无流、正向流和反向流作用下,珊瑚礁剖面上波高(H)和平均水位(MWL)的沿礁变化。图3a表明:波浪从外海向珊瑚礁海岸传播过程中,在礁前斜坡上发生浅水变形,波高显著增大,随后在礁缘附近发生破碎,波高剧烈下降,在礁坪上由于礁面摩擦消耗能量,波高沿礁缓慢减小。对比不同流的情况发现,在正(反)向流的影响下,波高的最大点(波浪破碎点)向海岸(外海)侧移动;在礁坪上,透射波高在正向流时显著大于反向流,这是由于正(反)向流的存在减弱(加剧)了波浪的非线性,因此在礁坪能形成的稳定的透射波就越大(小)。

图3 波高(H)和平均水位(MWL)的沿礁变化(x=0表示礁缘位置,以向岸方向为正)

在图3b中,礁缘之前的平均水位均低于静水位,这与水槽中水的质量守恒有关,即破碎带后的增水的产生要与远海的水质量损失守恒。波浪在礁前斜坡由于浅化变形,使得平均水位进一步下降。在礁缘附近,波浪发生破碎,平均水位急剧增加。在礁坪前端附近增水达到最大值,随后在礁坪中间附近开始沿程逐渐降低,这与Gourlay[13]瀉湖开放的情况一致,主要是受到礁坪水流的影响。破碎带内由于波高衰减幅度(代表辐射应力的梯度)的不同导致平均水位发生变化,对比不同流的影响发现,总体而言,反向流影响下(此时波高衰减幅度最大)礁坪上的波浪增水大于正向流影响下(此时波高衰减幅度最小)的平均水位,这与前述结论一致[9]。

2.3 波浪偏度、不对称度和厄塞尔数的沿礁变化

波浪从外海向珊瑚礁海岸传播过程中,受珊瑚礁陡变地形的影响,在礁坪上传播时会呈现出明显的非线性特征,文献中通常采用偏度(S)、不对称度(A)和厄塞尔数(U)来描述波浪的非线性特性。其中,S代表了波浪相对水平轴的不对称程度,S正向变大时波峰变得尖锐,波谷变得平坦;A代表了波浪相对于垂直轴的不对称程度,A为负值和正值分别代表着波浪的整体前倾和后倾;U表示波浪的非线性强度。其计算公式如下:

(1)

(2)

(3)

图4表明:对于无流的情况,波浪在礁前斜坡坡脚之前S、A及U值均接近于零,这是因为波浪在该阶段的传播过程中较为稳定,接近于线性波的波面形态。随着波浪在礁前斜坡处发生浅化变形,波面形态表现为波峰变尖及波谷变坦,波浪整体前倾且波峰变陡,波浪的非线性显著增强,S值与U值逐渐增大,A值则从零开始逐渐减小;S最大值出现在破碎带结束处,A的负峰值出现在内破碎带,U的最大值出现在破碎点附近,这与前述结论一致[7];随后波浪破碎结束后在礁坪上传播时,由于重新生成了波面稳定的透射波,S值与U值逐渐减小接近于零,A值则逐渐增大接近于零。礁坪上的A与S值也存在明显的振荡现象,主要是由于破碎带内的自由高频波和锁定高频波在礁坪上以不同的速度释放所致[14]。

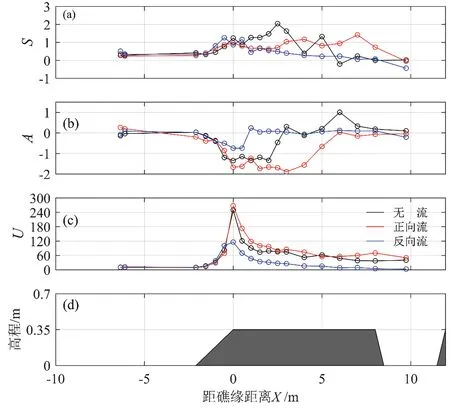
图4 波浪偏度(S)、不对称度(A)以及厄塞尔数(U)的沿礁变化(x=0表示礁缘位置,以向岸方向为正)

对比正反向流与无流的影响时,图4a表明:S的峰值发生的位置随着流从反向变成正向往海岸方向移动,这主要是由于前述破碎点随着流向的改变而向岸移动造成;对整个礁坪而言,正(反)向流相对于无流增大(减小)了S值, 这主要与波高相关,正向流时礁坪上波高更大(见图3),波浪非线性更强,更易产生垂向的不对称性。图4b表明:A的负峰值发生的位置随着流从反向变成正向同样向海岸方向移动,这也是由于破碎点移动造成;在外礁坪附近,正(反)向流相对于无流增大(减小)了A的绝对值,这是因为正(反)流促进(抑制)破碎波的前倾,波浪破碎结束后,两者的A值在内礁坪趋于一致。图4c表明:破碎点的移动对U的峰值的位置影响不大,但是随着流从反向变成正向,从破碎点起整个礁坪的U值增大,参照公式3,这与波高的增大,增水的减小(代表礁坪水深的变化)相关(见图3),同时由于前述的多普勒效应,波长也随着流向的改变增加。

2.4 高次谐波

波浪作用于珊瑚礁浅水地形时,由于地形变化剧烈,在礁缘附近比平直海岸更易产生高次谐波。本文通过快速傅里叶变换(FFT)对测得的自由液面时间序列进行谐波分析来研究高次谐波的沿礁变化规律。

图5展示了有流和无流作用下各次谐波振幅(a1～a5,精确到五阶)的沿礁变化规律。从总体上看,总波幅at沿礁变化主要由主频波波幅(a1)决定,波浪在礁前斜坡上传播时,由于浅化作用,a1显著增大。随后波浪在礁缘附近发生破碎,波能耗散剧烈,a1急剧减小,直到波浪在礁坪上重新生成行进波,a1趋于平稳。当波浪在礁前斜坡上发生浅化变形时,高次谐波振幅(a2～a5)由于波浪非线性作用逐渐增大,且均在破碎点附近到达峰值,随后a2～a5在礁坪上由于摩擦损耗而逐渐降低。

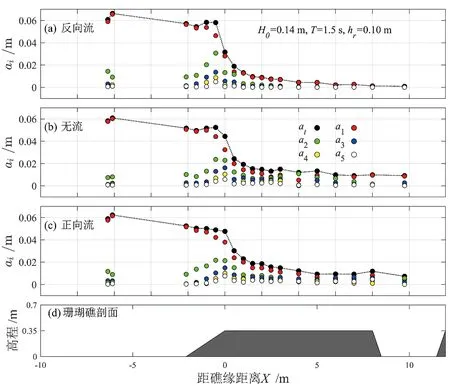
图5 总波幅(at)以及各次谐波振幅(a1～a5)的沿礁变化

对比不同流的影响发现:a1的变化与图3a中波高H的变化趋势一致;相比于无流的情况,在破碎点附近反向流促进了高次谐波(a2～a5)的增大,正向流则削弱了该处高次谐波;在礁坪上,a2～a5在反向流存在时衰减更为显著,其在正向流存在时衰减幅度小于无流时,这与a1的衰减规律一致。

3 结论

本文通过物理模型试验对潮汐流影响下波浪在珊瑚礁海岸地形上的传播变形和非线性特征展开研究,分析了典型工况下正向流和反向流存在时波面时间序列、波高、平均水位、非线性特征参数和高次谐波的沿礁变化规律,并与无流的情况进行了对比。结果表明:相对于无流的情况,由于发生了多普勒频移效应,正向流的存在造成礁坪上波浪的相位前移,反向流则造成了相位滞后。在正向流的影响下,波浪破碎点向岸侧移动;反向流影响下,破碎点则向外海侧移动;礁坪上正向流存在时的透射波高显著大于反向流存在时的透射波高,而正向流存在时的波浪增水则小于反向流存在时的波浪增水。随着流从反向变成正向,偏度的峰值与不对称度的负峰值发生的位置随着波浪破碎点的移动而移动,而厄塞尔数的峰值位置却几乎不变;在礁坪上,正(反)向流相对于无流增大(减小)了偏度和不对称度的幅值,厄塞尔数则随着流向由反向变正向而逐渐增大。在礁缘波浪的破碎点附近反向流促进了高次谐波的增大,正向流则削弱了该处高次谐波,礁坪上高次谐波在反向流存在时衰减幅度最大,正向流存在时衰减幅度最小。