元素存在形态对地球化学敏感性指数的影响研究
2024-04-01张晓艺栾永霞郑西来孟春霞
张晓艺,栾永霞,阎 妮,郑西来 , 孟春霞
(1.海洋环境与生态教育部重点实验室,山东 青岛 266100;2.中国海洋大学环境科学与工程学院,山东 青岛 266100;3.青岛市城阳区农业农村局,山东 青岛 266109;4.中国海洋大学化学化工学院,山东 青岛 266100)
引 言
地球化学敏感性是地下水系统的固有属性,能反映该系统中某种元素对外界影响的敏感程度[1]。21世纪初,何守阳等[1]首次提出地球化学敏感性指数(geochemical susceptivity index,GSI)和地球化学敏感等值线(isosensitive line on geochemical susceptivity)的概念,开启了地球化学敏感性的定量研究。
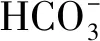
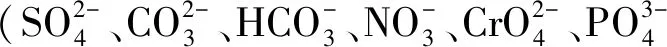
因此本文提出一种改进的GSI计算方法,在考虑单一离子形态和络阴离子态的基础上,增加实际水样中存在的络合形态,以得到更加精确的计算结果。以黄水河海水入侵区为例,分别用传统方法和改进方法对研究区进行GSI计算,通过将GSI计算结果与实际饱和指数(SI)进行对比,验证方法的可行性及准确性。
1 材料与方法
1.1 样品采集
研究区为黄水河流域中下游海水入侵区,位于山东半岛烟台龙口,属暖温带大陆性季风气候,降水量年际变化大,有明显的丰水期和枯水期。黄水河自东南向西北流入渤海,流域内整体地形呈东南高、西北低,主要地貌为侵蚀堆积倾斜平原区和堆积海滨条带阶地;主要的地下水类型为第四系孔隙水,广泛分布于黄水河中下游冲洪积平原、山前倾斜平原等主要地下水开采区。本研究利用研究区2019年枯水期和丰水期采集样品进行测试,共设有地下水采样点28个(缺失23号),地表水采样点1个(22号),海水采样点1个(16号,位于入海口)。将水样根据TDS含量进行划分,TDS <1 000 mg/L为淡水, TDS >1000 mg/L为咸水[15-17],分别确定2号、6号和16号水样为典型地下咸水样、地下淡水样和海水样。

图1 2019年9月份黄水河地下水源地采样点分布及地下水位等值线图
1.2 饱和指数(SI)计算
饱和指数是判断和确定矿物沉淀/溶解趋势的一项重要指标,用来判断水体中元素和周围岩石、矿物发生的反应,确定不同元素形态的迁移行为[18-19]。因此,本文将传统方法和改进方法计算的GSI与饱和指数对比,确定改进方法的可行性和准确性。本文首先利用软件PHREEQC[20]对研究区典型矿物饱和指数进行计算,其计算公式为:
(1)
式中,IAP为选择矿物相应组分活度积,无量纲;Ksp为选择矿物相应组分溶度积,无量纲。
当SI>0时,代表选择矿物处于过饱和状态,具有沉淀趋势;当SI=0时,代表选择矿物处于平衡状态,既不会沉淀,也不会溶解;当SI<0时,代表选择矿物处于不饱和状态,具有溶解趋势。
1.3 地球化学敏感性分析
根据何守阳等[1]提出的方法,地下水中某种组分i的GSIi被定义为:
(2)
式中,cli代表组分i枯水期浓度,chi代表组分i丰水期浓度,单位mmol/L;di为组分浓度点(cli,chi)到地球化学敏感等值线(直线cli=chi)的距离值,无量纲(图2);GSIi为组分i的地球化学敏感性指数,无量纲。
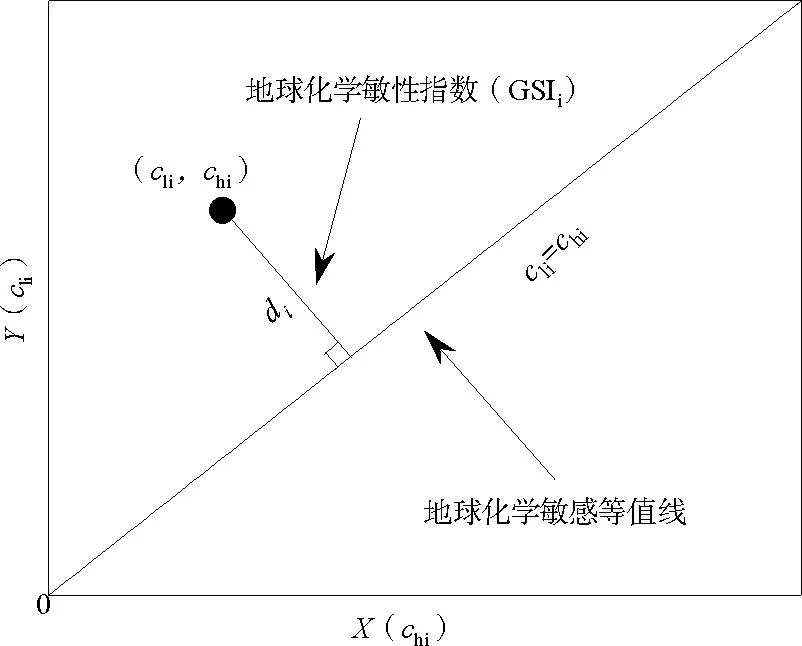
图2 地球化学敏感性指数及敏感等值线定义示意[1]
GSIi=0时,即cli=ch i时,表示该组分浓度在丰水期和枯水期没有变化,表现为无敏感性。组分i的地球化学敏感性指数GSIi的值越大,表示该组分的地球化学敏感性越高,越容易受到自然或人为因素的影响。
本文利用软件PHREEQC[20]计算三种典型水体枯水期和丰水期中Na、K、Ca、Mg、Cl、S、C等元素存在形态以及每种形态含量,进一步得到每种组分的GSI。最后将改进方法和传统方法计算结果与饱和指数进行对比验证,确定改进方法的准确性。
2 结果与讨论
2.1 水化学特征分析
典型水样丰水期和枯水期野外检测结果如表1,主要成分含量如表2。
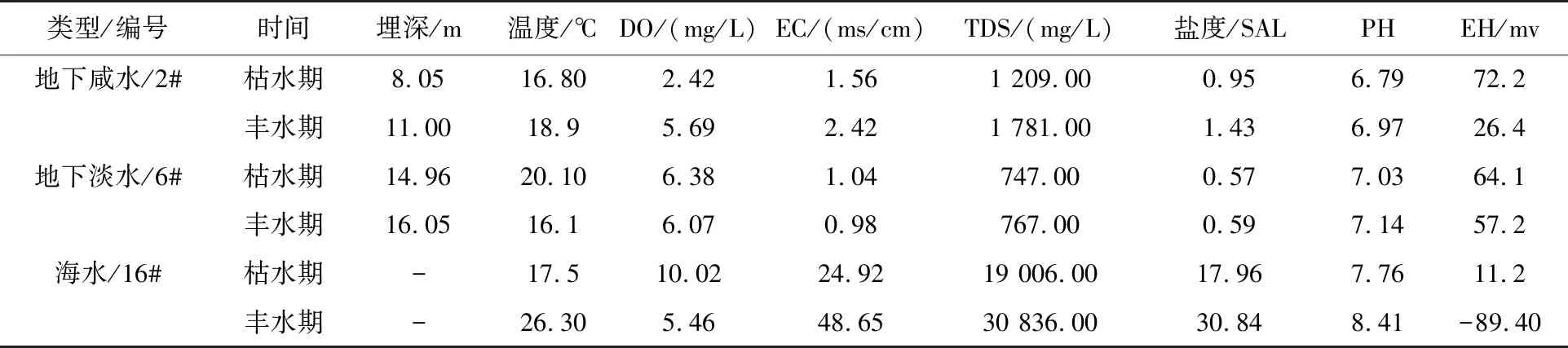
表1 典型水样野外测量结果

表2 典型水样主要成分含量
地下咸水样和地下淡水样pH均接近中性,海水呈弱碱性。相比较于6号地下淡水,2号地下咸水和16号海水丰水期TDS分别比枯水期上升47%和62.2%。这是因为丰水期地下水埋深降低(表1), 导致海水入侵更加严重,地下水中海水所占比例上升,从而导致TDS增大。这一现象随着距海岸线距离的减小而更加明显。

16号海水样不论是枯水期还是丰水期,离子含量普遍高于地下咸水和地下淡水。其中,Na+含量占阳离子毫克当量的70%,Cl-含量占比超过阴离子毫克当量的90%。这是因为海水中浓度最高的两种离子即为Na+和Cl-。
2.2 典型水样饱和指数
为验证改进后地球化学敏感性指数计算方法的准确性,利用软件PHREEQC分别计算三种典型水样枯水期和丰水期饱和指数,确定元素变化趋势。计算结果如图3。

图3 典型水体饱和指数 a为2号地下咸水;b为6号地下淡水;c为16号海水
从图3可以看出,三种典型水体矿物饱和指数整体趋势均为碳酸盐型>硫酸盐型>氯化物型,海水>地下水。
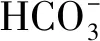
2.3 典型水样地球化学敏感性
2.3.1 水样组分存在形态
由于传统方法只能得到元素总量,无法得到元素每种存在形态的量,而络合形态的存在会改变元素在地下水中的迁移能力,影响沉淀/溶解和吸附作用。因此,改进方法利用PHREEQC计算典型水样元素存在形态及浓度。计算结果如表3,表中仅展示含量超过1%的组分存在形态。
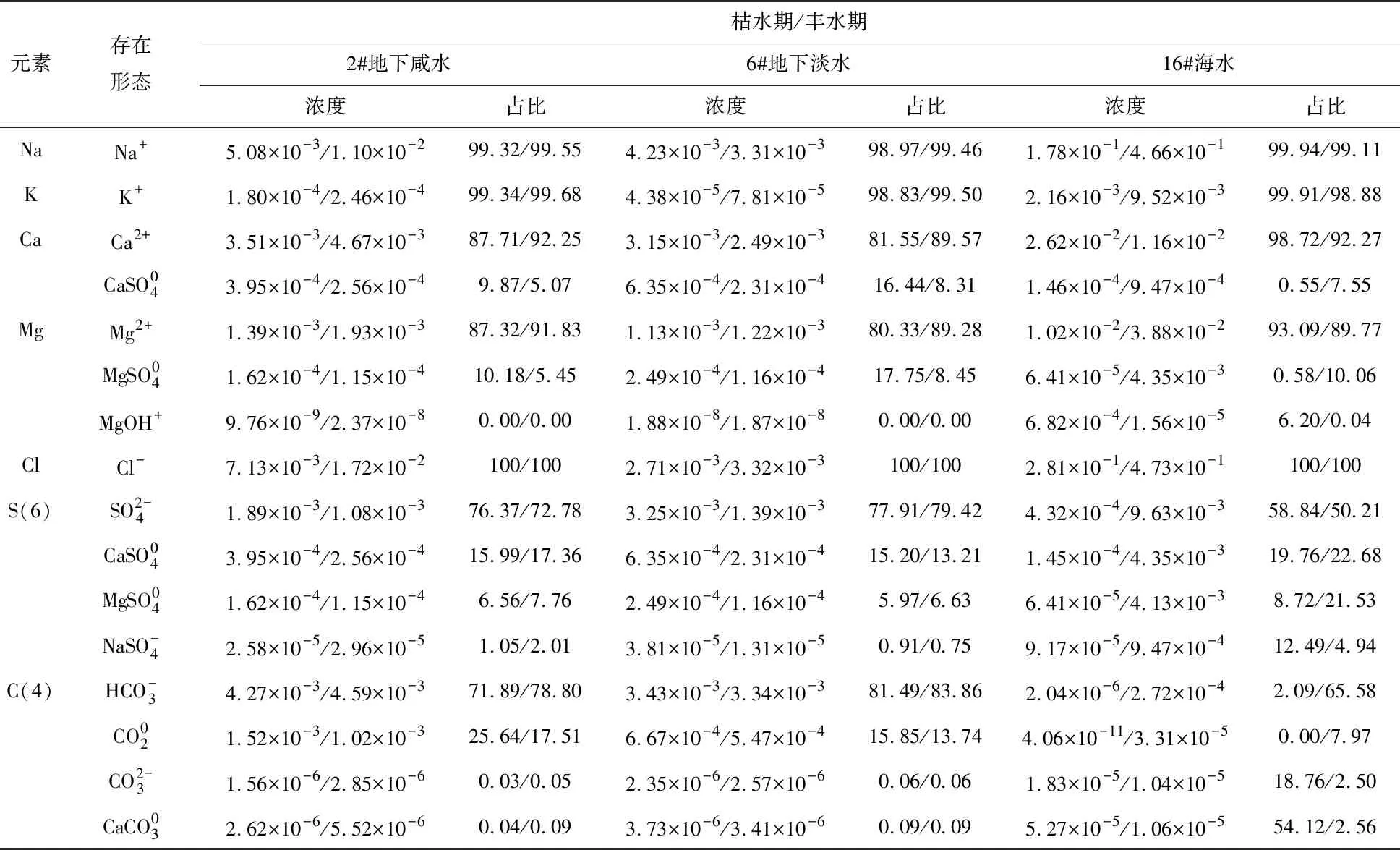
表3 丰水期典型水样组分主要存在形态浓度(mol/L)及其在该元素总量的占比(%)


从以上分析可知,不论是阳离子还是阴离子,用元素总浓度代替单一离子和络阴离子浓度会使计算结果偏大,产生不可忽视的误差。考虑络合组分含量、占比的变化能够更加准确地判断当地地球化学敏感性。因此,在对研究区进行地球化学敏感性分析时有必要考虑元素的组分分布形态。
2.3.2 组分地球化学敏感性分析
从表4可以看出,三种典型水体地球化学敏感性指数总体趋势为:海水 >地下咸水 >地下淡水,这说明海水入侵对研究区水文地球化学作用有较大影响。
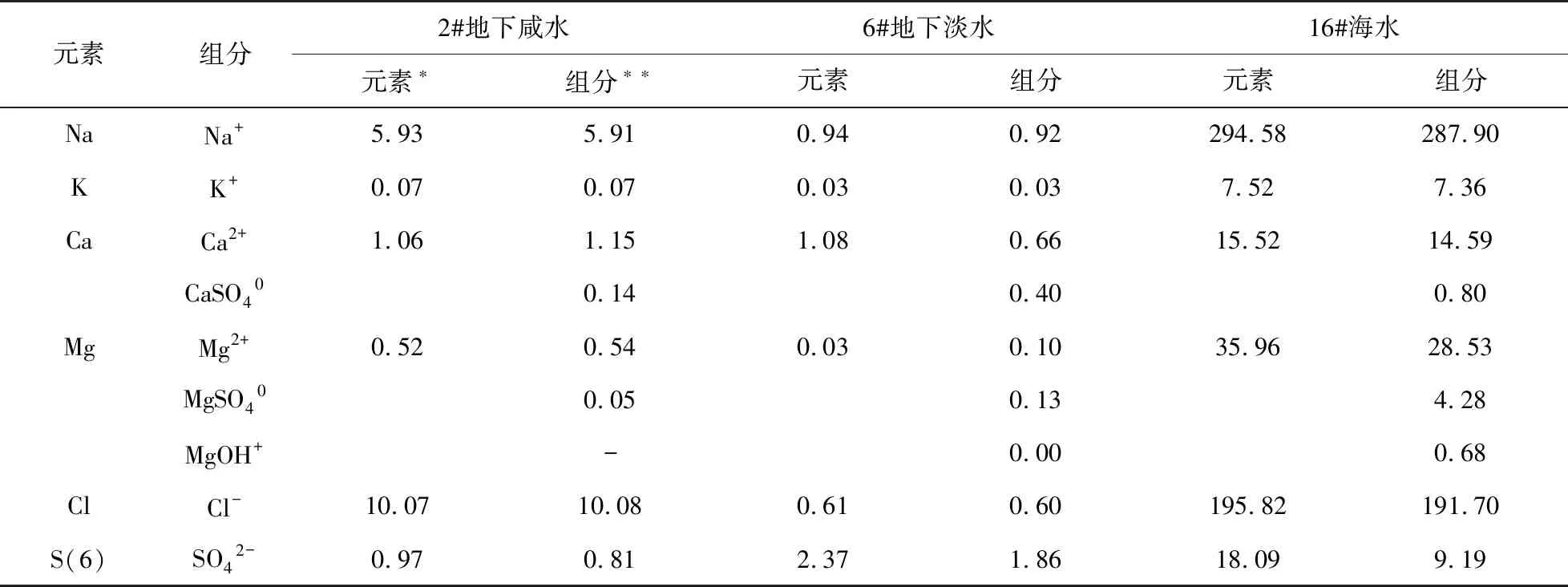
表4 元素及其组分存在形态地球化学敏感性指数
由于水体中有一定比例的元素以络合形态存在,传统方法计算的GSI其实是单一离子、络阴离子与络合组分GSI总和,而改进方法将单一离子态、络阴离子态与络合组分GSI分别进行计算,所以改进方法能够得到更加准确的结果。
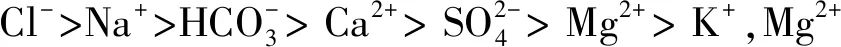
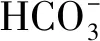
从以上分析可以得出,改进方法计算得到的GSI更加准确。如果不考虑组分存在形态的多样性,仅以元素总浓度代替组分浓度进行计算,得到的GSI值普遍偏高,其分布反映的水文地球化学作用偏离实际情况。因此,在计算时有必要考虑组分存在形态,得到更加准确的GSI。
3 结论
(1)通过改进方法计算研究区典型水样GSI,得到三种水样GSI趋势为海水>地下咸水>地下淡水。
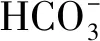
(3)计算结果表明,络合组分在三种典型水体中均表现出一定敏感性,其中海水中敏感性最高。因此在进行地球化学敏感性判断时不可以忽略组分的存在形态,尤其是计算海水入侵区GSI时,有必要将每种存在形态的GSI单独计算。
