基于磁导率无损检测的双U型探头仿真优化研究*

2024-04-01邓文洁任尚坤

焊管 2024年3期

邓文洁，任尚坤

（南昌航空大学无损检测技术教育部重点实验室，南昌 330063）

0 前言

铁磁性材料是当前工业应用的基础性材料，在一些大型建筑比如铁路、航天工程、油气管道[1-2]中广泛应用。铁磁性材料长时间反复受力承重，会导致材料本身出现疲劳损伤、应力集中、裂纹等缺陷，极易引起严重的安全隐患[3]甚至发生重大事故危及人身安全。因而，检测和防治铁磁性材料的缺陷与寿命具有重大意义[4]。

磁导率检测技术是一种由试件缺陷引起磁导率变化的新型检测方法。通入激励信号的传感器对应力集中、疲劳损伤等缺陷进行检测，再由磁导率的变化引起输出信号的变化进行评价。早期的磁导率检测技术是由Vértesy 等[5-7]指出，采用磁适应检测法研究了热老化时间对钢脆化状况的影响，并与传统检测方法进行了对比，得出磁适应检测法具有更高的检测灵敏度和可靠性。近年来，国内开始研究利用磁导率检测技术对缺陷进行无损检测，并偏向检测应力集中导致的磁导率信号变化。石松跃等[8]首先提出高微分磁导率的概念，是当时国内初步对磁适应检测技术进行的研究；吴德会等[9]提出了基于微分磁导率对宏观缺陷进行检测的新方法；邱忠超等[10]提出了一种磁各向异性检测铁磁构件应力的方法。

这些方法都需要利用探头输出的检测信号进行被检试件的缺陷判断，并且探头不会对试件本身造成伤害，这是一种真正意义上的无损检测[11]。因此，检测探头在磁导率技术中的作用尤为重要，探头的设计与研究同样成为目前研究热点之一。

在检测探头的研究领域，Yamada 等[12]研究了四脚磁探头检测试件应力的方法；魏明等[13]通过九脚探头中磁导率的变化，得出其与应力和检测电压的关系；王瑛等[14]设计了一种能将应力转换为阻抗的差动式压磁传感器，为压力传感器奠定了基础；殷春浩等[15]用四脚探头和载荷试验机对应力曲线进行了标定。

基于此，本研究依据电磁感应原理，将双U型传感器与磁导率检测技术相结合，对双U型探头产生的检测信号进行研究，通过仿真试验探究探头检测灵敏度的影响因素并对其进行优化选取。

1 磁导率检测模型

传感器骨架为正交U型锰锌铁氧体，由两个U 型探头P、Q 交叉放置构成。双U 型探头结构如图1所示。

图1 正交U型传感器结构示意图

图2 为传感器绕组示意图，在A1、B1 探脚上分别缠绕参数一致的正向激励绕组N-1、N-4，A2、B2探脚缠绕正向检测绕组N-3、N-2。

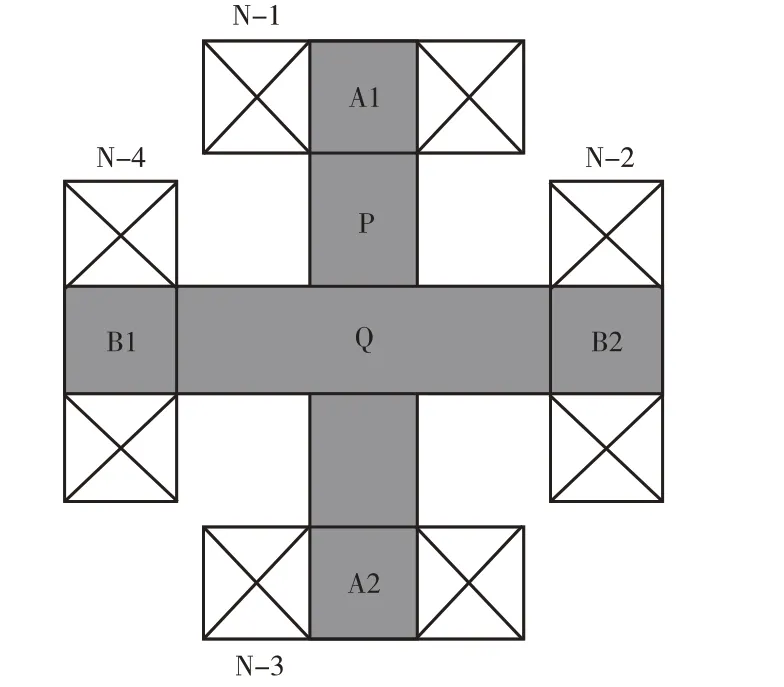
图2 传感器绕组示意图

向激励线圈通入激励交变电压，根据法拉第电磁感应定律，激励线圈N-1、N-4 处磁轭内分别会形成走向检测线圈磁轭内部及被测试件的闭合磁回路。当被检试件内部存在微观结构变化引起的缺陷时，会导致磁导率的改变，继而影响输出信号的变化。相较于传统单个U 型探头，双U型探头具有测量方向更多、试验精度更准确等特点。

向N-1、N-4 通入正弦激励交流信号时，依据磁路环路定理和磁路的欧姆定律[16]

式中：Rm——磁回路中的磁阻；

H——磁路中的磁场强度；

l——积分路径；

Φ—磁回路磁通量；

i——激励电流。

可得线圈磁通量

式中：Φ1、Φ2——探头P、Q通过的磁通量；

N1——激励线圈匝数；

R1m.out、R2m.out——探头P、Q磁回路的磁阻；

μ——被测试件的磁导率；

S——待测试件的等效横截面积；

L——待测试件有效区域长度。

根据Maxwell第二方程

代入（2）式、（3）式得P、Q感应电压为

式中：N2——检测线圈匝数；

E——感应电磁场强度；

B——磁感应强度。负号表示电流产生的磁通量方向与电压相反。由上式可知，当线圈匝数、试件大小、探头磁轭磁阻及被测试件自身的磁导率发生变化时，都会影响输出信号发生改变，最终能反映出试件内部结构的变化。因此，研究优化检测探头的参数有助于提高试验检测灵敏度。

2 双U型探头参数优化

2.1 探头建模

运用仿真软件对双U 型探头进行三维建模。首先确定仿真所需要的环境磁场，再进行不同参数的仿真优化。仿真流程如图3所示。

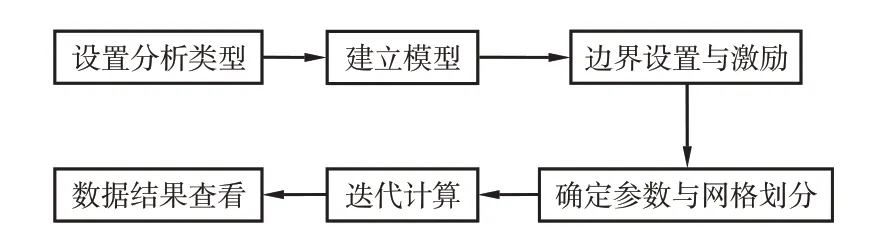
图3 仿真流程图

设置环境磁场为涡流磁场，建立探头模型，双U 型外层探头P 尺寸为32.5 mm×9.9 mm×22.6 mm，梁高8 mm；内层探头Q尺寸为32.5 mm×9.9 mm×12.75 mm，梁高6.3 mm，探头P、Q相互独立正交放置未紧贴。选定探头材料为锰锌铁氧体，其相对磁导率μS取2 300，线圈材料为铜。选定20 钢为待测试件，其相对磁导率为相对应B-H曲线关系。激励线圈分别缠绕在探头P、Q的同侧磁轭上，形成磁回路。检测线圈分别缠绕在相对应的磁轭上作为检测信号输出，其中探头P 与探头Q 上的线圈对称缠绕。对探头线圈进行参数化设置，激励线圈通入正弦波激励电压源。探头结构仿真如图4所示。

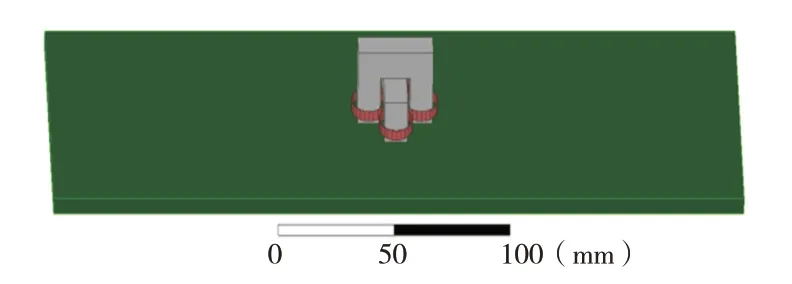
图4 探头结构仿真图

在固体模型建立完成时，需要考虑到空气域的影响，构建一个几何空间包裹模型形成求解域。在参数化步骤中勾选A1、B1 探脚绕组电感矩阵。在分析求解步骤中收敛步数设置为12，其余参数为默认值。

通过仿真分析得出双U型探头内的磁感应强度走向情况（如图5所示），当给N-1、N-4分别通入激励信号时，探头P、Q 内磁感应强度的方向都是从激励端流向检测端。

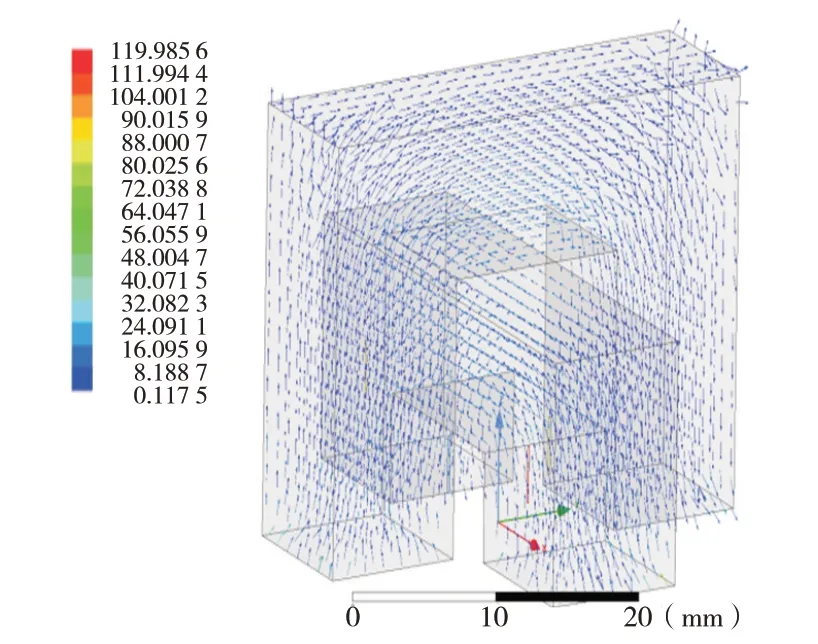
图5 双U型探头内磁感线走向

2.2 激励频率对检测灵敏度的影响

试件在被检测过程中，其激励频率会影响感应电磁场在试件内的检测强度，因而研究检测灵敏度的最优激励频率是必要的。在分析步骤中设置频率化扫描，激励电压设置为5 V。当激励电压一定时，分析检测灵敏度与激励频率的关系。

图6 所示为传感器P、Q 探头的灵敏度与激励频率关系。图6（a）和图6（b）中各有三条曲线，分别为铁磁回路曲线、空气回路曲线和铁磁与空气回路的差值曲线。检测灵敏度定义为空气与铁磁回路的输出电压之差，其最佳参数由检测灵敏度最高处，即二者输出电压之差最大值确定。

图6 探头检测灵敏度随激励频率的变化曲线

通过图6 可以看出，随着激励频率的增大，铁磁回路和空气回路的检测灵敏度先升高后趋于稳定，检测灵敏度在激励频率100 Hz 时达到最大。但根据趋肤效应，频率增大会使趋肤深度变浅，传感器检测范围降低，不利于被测试件的缺陷检出，所以在选取最优激励频率时，不应选择过高频率，本次最优频率均选取80 Hz。探头Q与探头P相比，检测灵敏度较低，这是因为其探脚较探头P 略短，磁通量通过磁轭的路径变短，通过的磁通量减少所致。由于探头P、Q 有类似的输出信号变化，因此下文仅说明探头P的相关参数对检测灵敏度的影响。

2.3 激励电压对检测灵敏度的影响

在参数化扫描步骤中，设置激励电压为变量，使线圈通入2～12 V 的电压，步长设为2 V。通过仿真电磁场分析结果可知，检测灵敏度与激励电压有关，图7 所示为6 种不同激励电压与检测灵敏度的关系。

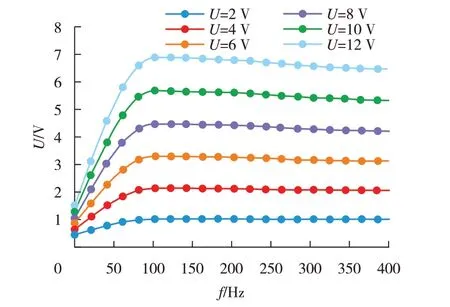
图7 不同激励电压下检测灵敏度随频率的变化曲线

由图7可以看出，当激励频率一定时，检测灵敏度随激励电压增加而变大。随着激励频率的增加，不同激励电压下的检测灵敏度变化趋势类似，均为先升高而后保持稳定。当激励电压增大时，检测灵敏度在激励频率为80 Hz 时均达到最大值，说明最优激励频率与激励电压的变化无关。

图8 所示为激励频率为80 Hz 最优频率时，激励电压与检测灵敏度的变化关系。由图8 可知，随着激励电压的增大，检测灵敏度升高，二者呈线性关系。但在实际试验中，激励电压并非越高越好。原因是当输入的激励电压过高时，传感器会出现轻微振动并伴随着一定的发热情况，产生噪声且受到其干扰，导致后续试验结果受到影响。因此可将激励电压幅值设置为中间值6 V，以避免非必要的因素干扰试验。

图8 激励电压与检测灵敏度关系曲线

2.4 激励线圈匝数对检测灵敏度的影响

为了研究激励线圈匝数与检测灵敏度的关系，将激励磁线圈匝数设置为变量，其他参数保持不变，当激励电压幅值一定时，不同激励线圈匝数下检测灵敏度随激励频率的关系曲线如图9所示。从图9可以看出，检测灵敏度与激励线圈匝数有关。当激励频率一定时，随着激励线圈匝数的增加，检测灵敏度递减，但最优激励频率仍保持不变。

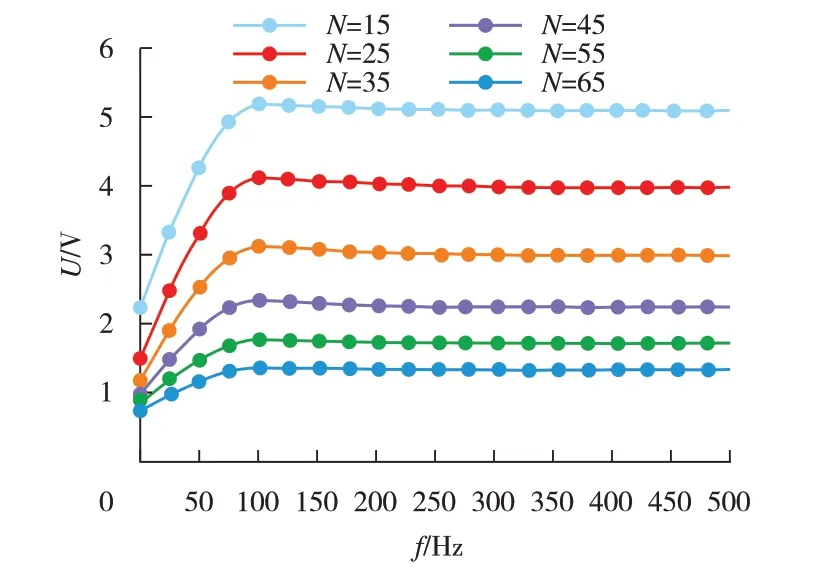
图9 不同激励线圈匝数下检测灵敏度随激励频率变化关系

最优激励频率下，检测灵敏度与激励线圈匝数的关系变化如图10 所示。由图10 可见，检测灵敏度与激励线圈匝数二者为非线性关系，随着激励线圈匝数的增大检测灵敏度递减。

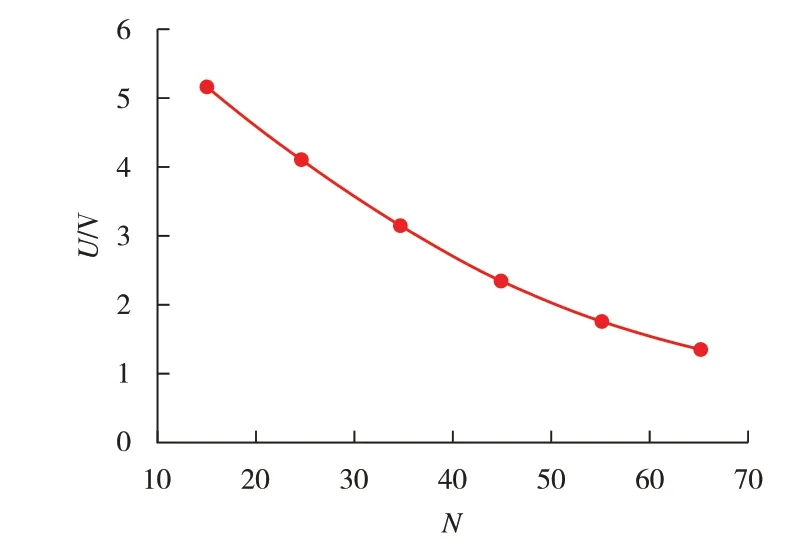
图10 激励线圈匝数与检测灵敏度的关系曲线

分析出现这种现象的原因，由电感经验公式可知

式中：L1——激励线圈电感；

k——线圈形状的修正系数；

μ0、μS——分别为真空磁导率与相对磁导率；

S——截面面积；

l——线圈长度。

当k、S、μ0、μS、l一定时，电感与电阻平方成正比关系。以探头P 为例，将式（5）改写可得

式中：R——激励线圈电阻。

由式（8）可知输出电压与电感成反比关系。联立式（7）和式（8）可得

式中：A、B、R——定值；

ω——角频率。

由式（9）可知，当激励线圈匝数增加时，电感增加，输出电压随之降低，即检测灵敏度降低。由图10 可知，当激励线圈匝数选择15 匝时，检测灵敏度最大。但选用激励线圈缠绕匝数时应注意，匝数过低会使传感器中磁路磁感应强度迅速变高达到磁饱和状态，进而引起电流大大增加出现发热现象。同时匝数过高会导致磁路的磁感应强度下降，影响检测灵敏度。综上，最优激励线圈匝数选用25匝可避免以上问题。

2.5 不同探头的仿真对比分析

鉴于上文对双U 型探头的激励参数优化结果，对传统单U型探头M进行仿真分析，使探头M 的尺寸与探头P 相同，在同样条件下将各激励参数幅值调至最佳的检测效果。图11 为探头M的检测灵敏度随激励频率变化曲线。

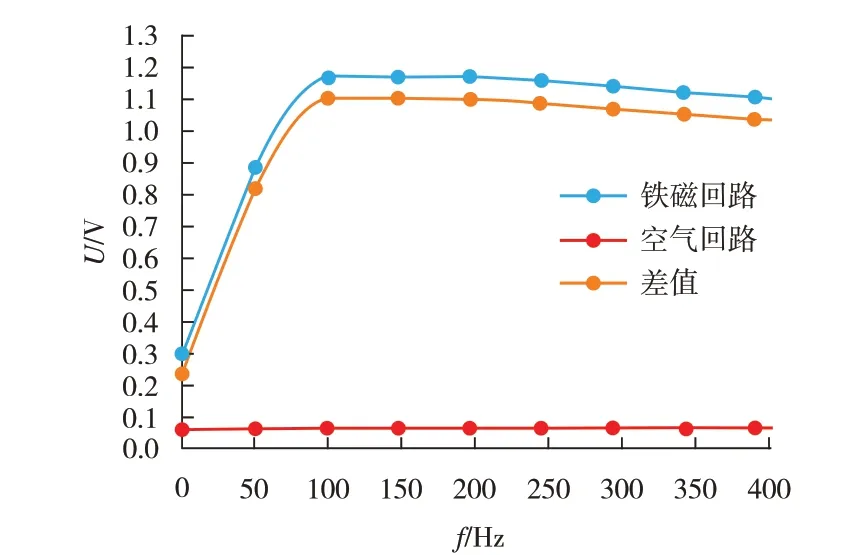
图11 单U型探头M检测灵敏度随激励频率的变化曲线

将双U型探头与传统单U型探头检测灵敏度进行对比，如图12所示。由二者对比分析可知，双U型探头在二维x、y方向上都能输出检测信号，即当探头P检测到水平x方向的拉应力时，由应力引起的输出信号变化也可被垂直y方向的探头Q同时检测到，而传统单U型探头M只能检测一个方向上的应力。相比于传统单U型探头，双U型探头的检测方向更广，与理论分析一致。

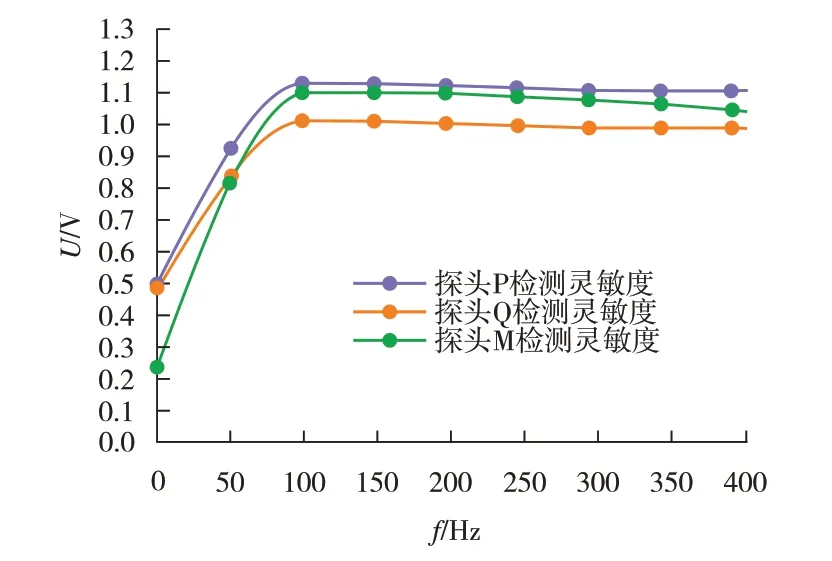
图12 双U型探头与传统单U型探头检测灵敏度对比

3 灵敏度检测试验验证

利用拉伸机对20 钢板进行静载拉伸试验，图13 为20 钢板试件的结构尺寸，钢板试件厚度为2 mm。

图13 20钢板试件尺寸（单位：mm）

通过拉伸试验可知20 钢试件的屈服强度为394 MPa、抗拉强度为532 MPa。向试件施加0～30 kN 的轴向拉力。检测信号与拉应力的变化关系如图14所示。

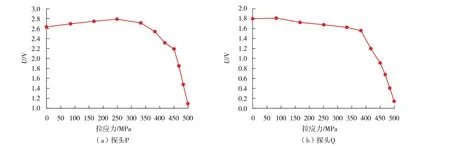
图14 探头灵敏度随拉应力的变化曲线

图14（a）和图14（b）分别为轴向、纵向的应力与检测信号变化。从图14（a）可以看出，当拉应力为100～350 MPa时，检测信号随拉力的增加略微起伏，变化不大；当拉应力为380 MPa接近屈服强度后，检测信号急速下降，即当拉应力大于弹性阶段变形所受的力时，检测信号会发生明显变化。图14（b）检测信号变化趋势为先缓慢下降再急剧减小。

试验结果表明，双U型探头可以同时检测两个方向的应力变化，基于磁导率技术的检测灵敏度可以用于检测试件受力的状态。