基于Jaya算法的LPI雷达波形设计
2024-04-01周明月周建江张丹枫
周明月,周建江,叶 雷,杨 忠,张丹枫
(1. 上海航天电子技术研究所, 上海 201109)(2. 南京航空航天大学 电子信息工程学院, 江苏 南京 211106)
0 引 言
雷达技术需要朝着“先敌发现、先敌攻击”的方向发展[1]。 由于实现雷达低截获的首要问题是其发射的信号本身就不容易被截获,所以波形设计一直都是低截获雷达研究的热门领域。雷达信号的发射和接收是一种信息的传输和处理过程,信息论在雷达信号的波形设计中发挥着重要的作用[2-4]。
文献[5]首次提出通过最大化目标和回波信号之间的互信息提升雷达的探测性能。随后,互信息和Kullback-Leibler(KL)距离等信息论工具在设计雷达信号波形中的应用层出不穷。文献[6]在有色噪声环境中,针对扩展目标研究了最优雷达波形的设计问题,并给出了输出信噪比、KL距离和互信息之间的关系,揭露了基于信息论的波形设计各种指标之间的关系。然而,现有的波形设计方法主要着眼于雷达的任务性能,对雷达的抗截获性能的研究较少。文献[7]提出将信号与背景噪声之间的KL距离作为评估敌方拦截接收机性能的实用指标,建立了低截获概率雷达波形设计的多目标优化模型。
波形设计的优化准则层出不穷,但是许多波形优化问题的求解非常复杂,确定性算法如内点法、序列二次规划算法以及线性规划等传统的优化算法在求解组合优化问题时,面临的主要问题就是复杂度过大。此外,这类算法对优化参数初始值有着较强的依赖性,算法容易陷入局部优化。因此,寻找效率更高、普适性和鲁棒性更强的优化算法具有重要的实际意义。为了解决各种约束和无约束优化问题,优化领域迅速发展,研究人员提出了许多全局优化算法,避免局部优化现象的发生,且这类算法具有较少控制参数的优势。本文使用基于种群的优化算法来找到复杂波形优化问题的近似最优解,比传统优化算法通用性更好,且不依赖初始值的选取,寻优过程只用目标函数信息,而不用推导过程或其他辅助信息。
1 LPI雷达信号波形设计方法
雷达通过处理回波信号能获取多少目标信息可通过计算回波信号与目标散射信号之间的互信息来衡量。互信息越大,表明雷达从接收到的回波信号中获得的信息越多,越有益于雷达对目标进行检测、跟踪、定位和识别。
实际上,雷达在处理回波信号时,可通过匹配滤波,获得额外的处理增益,而对于敌方无源探测设备来说,无法获得波形的先验信息,利用时频分析很难得到足够的处理增益。因此,LPI波形设计的核心思想是通过雷达任务性能的少量损失,换取敌方无源探测设备性能的严重衰减。
1.1 基于互信息的雷达信号波形设计
假设在目标方向上发射天线的辐射增益为Gt,来回的路径损耗分别为L1和L2,传输距离为R,接收天线的增益为Gr。雷达发射天线辐射的信号波形为s(t),该发射信号照射在空间中的脉冲响应为h(t)的目标上。则经过该目标散射后的信号如下
x(t)=α1·s(t)*h(t)
(1)
式中:α1是信号传播过程中的能量衰减系数,与Gr、L1和R有关,符号*表示卷积。
散射波经过大气传输后到达雷达的接收机处,增益为Gr的雷达接收天线将其截获。接收信号可表示为
y(t)=α2·x(t)+n(t)=β·s(t)*h(t)+n(t)
(2)
式中:n(t)为0均值的高斯白噪声;α2为能量衰减系数,与Gr、L2和R有关;β=α1·α2。
将雷达系统的操作带宽W划分成多个互不相交的子带,用Δf来表示子带的带宽,当Δf→0时,雷达接收到的回波Y与散射波X之间的互信息的离散形式可以表示为
(3)

1.2 对抗截获接收机的波形设计
假设雷达在探测过程中,其发射信号照射到目标的同时也被对方截获,此时雷达面临着置身于敌方打击范围内的严重威胁。从截获接收机的角度出发,其截获到的信号一般可写为如下形式[7]。
z(t)=γ·s(t)+n(t)
(4)
式中:γ表示发射信号到达截获接收机的能量损失。
高斯白噪声是公认的具有最佳LPI性能的波形,那么,设计的信号与高斯白噪声的相似程度越大,截获接收机也就越难对信号进行检测、识别。KL散度以准确性高和计算复杂度低的优势成为度量变量信息的一种备受青睐的方法。在每一个频点上,截获信号Z与高斯白噪声N之间的KL距离表达式如下。
(5)
从式(5)可以看出,在每个频点上的KL距离都跟波形的功率谱密度和噪声功率谱密度的比值有关,这意味着截获接收机所截获到的信号的信噪比越低,其正确分选出该信号的概率越低。
1.3 基于雷达互信息和截获接收机KL距离的LPI信号波形设计
雷达的性能可用互信息I(X;Y|S)表示,截获接收机的性能可用KL距离D(Z;N|S)表示。雷达LPI波形设计的优化问题可以表示如下。
(6)
式中:PS是雷达平均发射功率。
式(6)的优化问题是一个多目标优化问题:在一定的发射功率约束下,同时满足雷达的任务性能和低截获性能。这其实是一个矛盾的问题。考虑到目标探测和识别等是雷达的首要性能,因此低截获概率波形的优化问题可以转变为在满足一定的雷达任务性能的条件下,最小化截获接收机的性能,即
(7)
2 基于Jaya优化的约束波形设计
Jaya算法是基于全局搜索的种群优化算法,由印度学者Venkata Rao于2016年提出[8-9]。 该算法的基本概念是针对给定问题获得的解决方案应朝着最佳解决方案发展,而应避免最坏的解决方案。文献[8]中使用多种测试函数对算法的收敛性和稳定性进行了分析,统计数据表明仅需较少的函数评估即可实现全局最优。Jaya算法不需要任何特定于算法的控制参数,在神经网络训练[10]、损伤识别[11]、结构优化[9]、机械工程[12]等领域均得到了广泛的关注和研究。以下是Jaya算法的详细步骤。
(1) 对于一定数量的种群,根据优化问题的可行域,随机生成具有个个体的种群,其中每个个体的维度与优化问题中的变量个数一致。
(2) 利用代价函数计算每一个个体的适应度,然后选出种群中“最佳”和“最差”的个体。
(3) 根据更新函数,利用“最佳”和“最差”的解,对种群进行更新
Xnew=X+r1(Xbest-|X|)-r2(Xworst-|X|)
(8)
式中:r1和r2作为缩放因子,是每个个体更新时产生的0到1的随机数。对更新后的个体再次计算其代价函数。
(4) 对比原先的代价函数和更新后的代价函数,由于这是一个最小化问题,将保留使代价函数最小的个体。
(5) 重复步骤(2)~(4),直到达到终止标准。
(6) 最终的优化结果提供了最优的波形设计结果,这些值是雷达发射波形在频域上的功率分布。
种群优化算法的应用已经相当成功,但是一个普遍的趋势是此类算法所解决的优化问题通常并不考虑约束,因此寻找合适的方法将约束合并到优化算法的适应度函数中是非常有必要的。
罚函数是一种常用的将约束优化问题转为无约束优化问题的方法[14]。其核心思想就是通过对违反约束的个体施加惩罚将其合并到适应度函数中。研究人员根据所需处理的复杂优化问题的特殊性,已经开发出大量处理约束的替代方法,如死亡惩罚、静态惩罚、动态惩罚、退火惩罚以及自适应惩罚等。在实际应用中,没有任何一种约束处理方法可以适用于所有问题,根据所需求解问题的一些特征决定使用哪种方法。
针对综合考虑雷达任务性能和抗截获性能的雷达波形优化问题,采用动态惩罚的方法加速收敛。为了方便讨论,先将式(7)中的等式约束改写为
(9)
将式(7)中的互信息不等式约束改写如下
(10)
则式(7)的优化问题可转化为如下形式
(11)
式中:C1和C2均为惩罚系数;t为迭代次数,可见对于互信息项的约束随着迭代次数的增加而加强。
3 仿真结果与分析

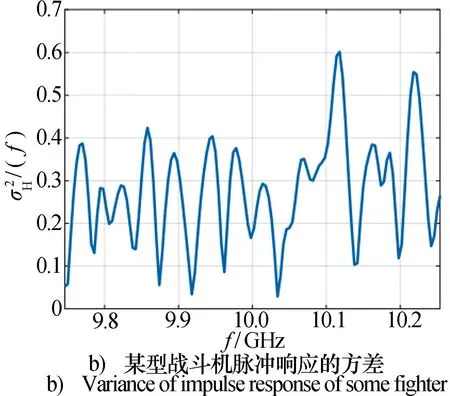
图1 某型战斗机的电磁模型与脉冲响应Fig.1 Experimental scenes under different noise backgrounds

表1 不同噪声背景下的实验场景Tab.1 Experimental scenes under different noise backgrounds
其中,高斯白噪声的单边功率谱密度为常数:PN(f)=1.953 1×10-18,有色高斯噪声的单边功率谱密度可设置为sinc函数,如式 (12)所示。为了体现有色高斯噪声对优化波形的影响,给出了有色高斯噪声的功率谱密度,如图2所示。

图2 有色高斯噪声的功率谱密度Fig.2 Power spectral density of colored gaussian noise
PN(f)=1.653 1×10-18×sinc(5.468 8×10-9×
f-51.607 2)+1.653 1×10-18,
f∈[9.746, 10.254]GHz
(12)
为了衡量所提算法在优化雷达性能和削弱截获接收机性能方面的效果,利用信噪比损失作为指标,其计算公式如下
ΔSNR=SNRMI-SNRMI-KLD
(13)
式中:ΔSNR是针对最大化互信息所设计的最优波形与综合考虑雷达任务性能和抗截获性能所设计的波形之间的信噪比差值。通过比较截获接收机和雷达的信噪比损失量,可直观地体现本节所提方法在波形优化方面的有效性。
除了表1中的背景噪声以外,其他的仿真参数详见表2。
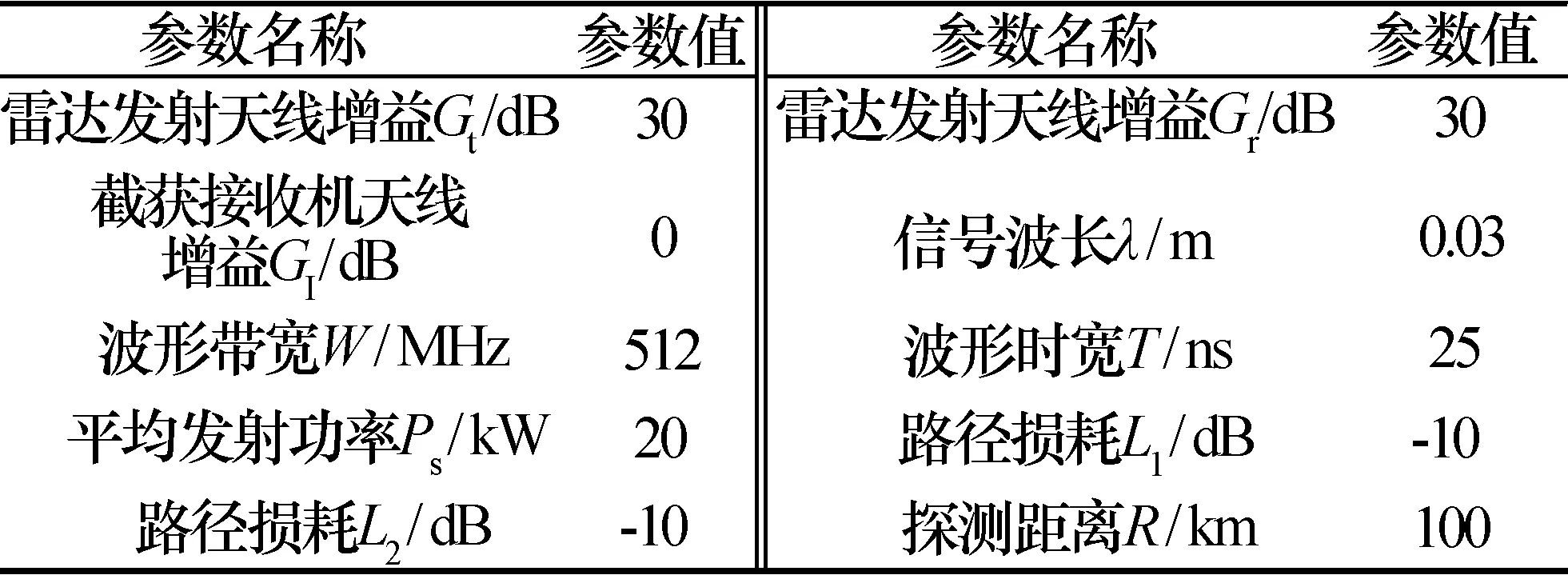
表2 仿真参数Tab.2 Simulation parameters
图3给出了联合优化雷达任务性能和对抗截获接收机性能的优化波形,根据设计的原则,将损失一定程度上的目标匹配度去换取截获接收机性能的严重衰减。为了更好地比较,在图中给出了仅考虑最优化雷达任务性能以及仅考虑最小化截获接收机性能这两种情况下的优化波形,分别标记为OP1,OP2。
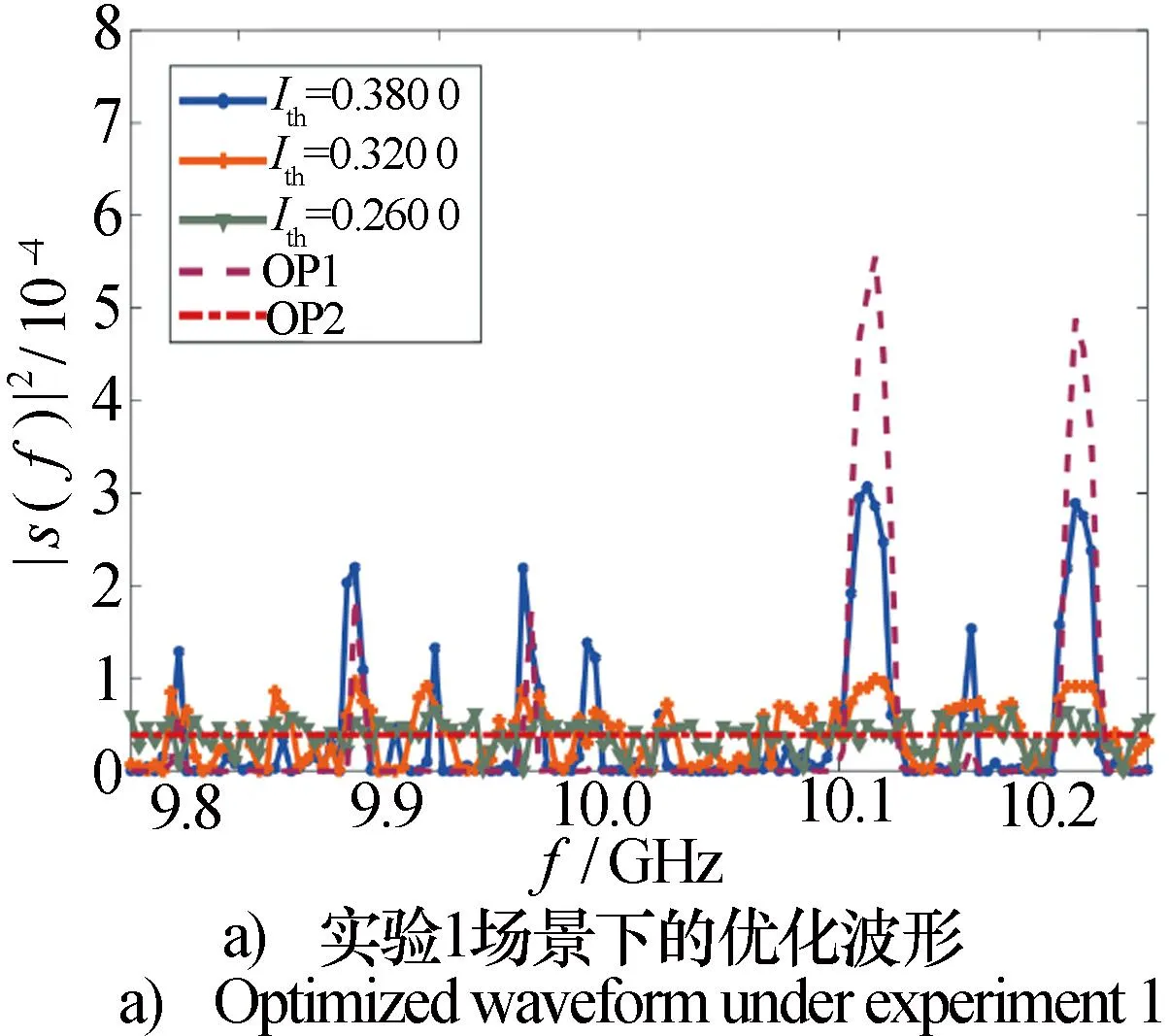
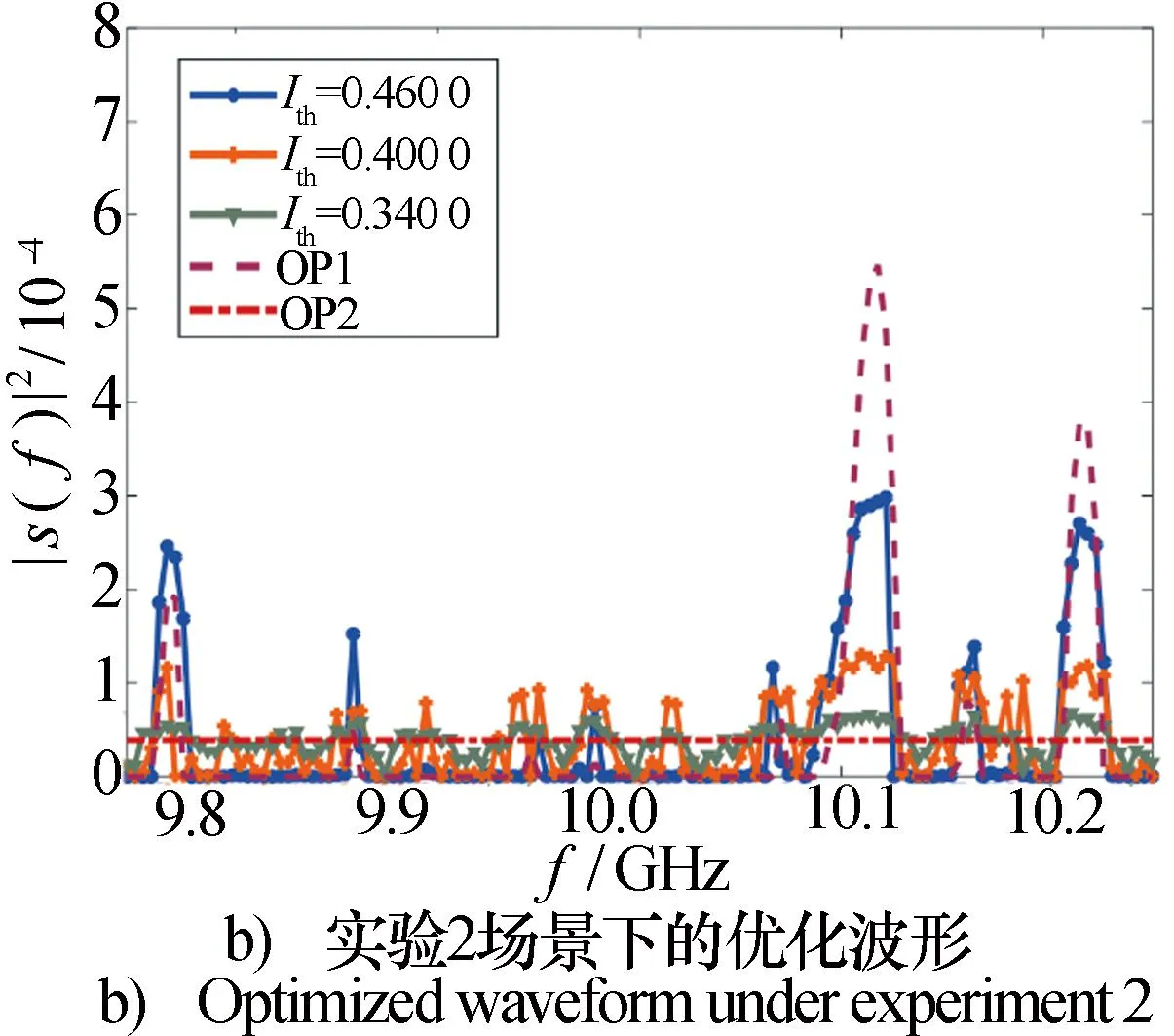
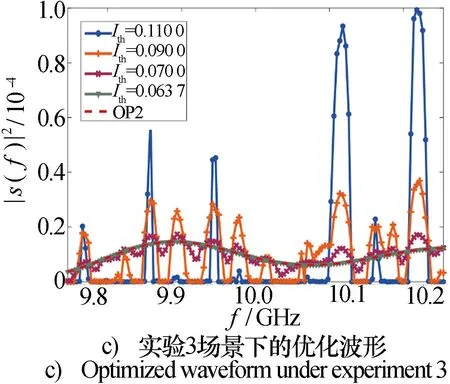
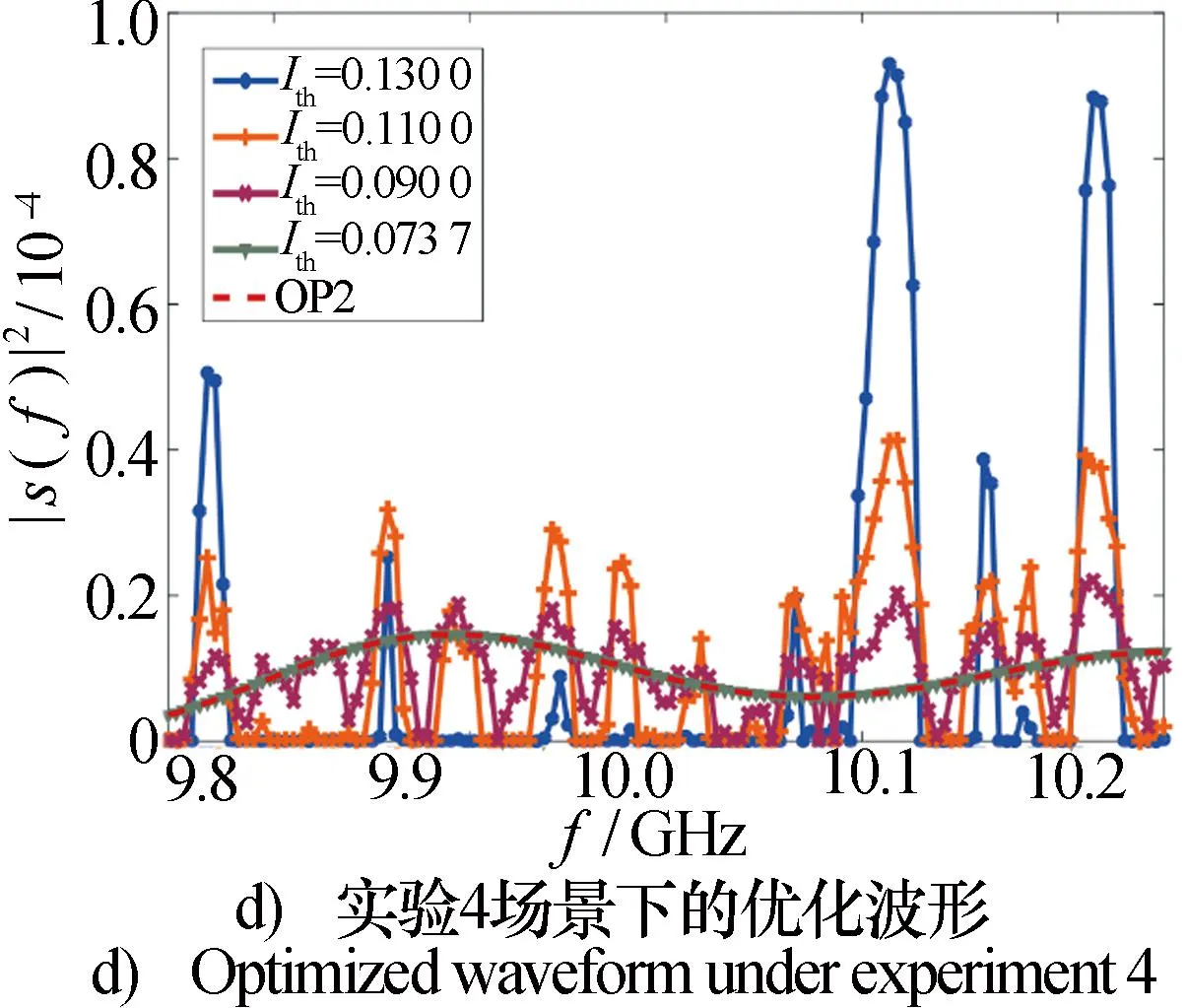
图3 不同互信息约束下优化的LPI波形Fig.3 Optimized LPI waveform under different information constraints
图3a)中,仅考虑最大化互信息优化时的优化波形所能达到的最大互信息为0.402 6。在互信息降为0.38时,如图3a)中蓝色曲线所示,优化波形的峰值几乎降为OP1的一半,此时,雷达损失0.601 9 dB的信噪比,而截获接收机已经损失2.576 9 dB的信噪比。所优化的波形既具有一定的目标匹配性能,又具有一定的抗截获性能。随着互信息约束的减小,优化波形的峰值得到明显的抑制,这可以从图3a)中的橙色加号线和绿色三角线看出,并且互信息约束越小,所优化的波形的形状就越接近OP2的波形。这体现了优化过程中,随着互信息约束的变化,对满足雷达任务性能和对抗截获接收机性能的权衡。
仅雷达背景噪声为有色高斯噪声时的优化波形如图3b)所示,仅考虑最大化互信息优化时的优化波形所能达到的最大互信息为0.474 1,这里选取了互信息约束分别为0.46、0.40和0.34等三种情况,画出了相应的优化波形。可以看出,优化波形的峰值随着互信息约束的减小而下降,并且在互信息约束值较大的情况下,优化波形的形状依然体现了有色高斯噪声的影响,但随着互信息约束的减小,这种特征被逐渐削弱,所优化波形的形状趋向OP2的波形。
仅截获接收机背景噪声为有色高斯噪声情况下的优化波形如图3c)所示。为了方便比较,将总功率约束降为5 kW。分析可知,最小化截获接收机性能的优化波形是以最小化每一个频点上的|S(f)|2/PN(f)为特征的。所以,OP2波形在频域上的分布与有色高斯噪声的功率谱密度一致。由图3c)中的蓝色圆点线可知,当互信息约束降为0.110 0时,优化波形已经体现出了OP2波形的特征,即优化波形在频域上的功率分配受到有色高斯噪声的影响。这也进一步证实了所优化的波形一方面与目标特性相匹配,另一方面也兼顾对抗截获接收机的特点。
由图3d)可见,对于雷达和截获接收机的背景噪声均为有色高斯噪声的情况,所优化的波形将随着互信息约束的不同在图3b)到图3c)之间变化。具体表现:当Ith的值较大时,如图3d)中蓝色圆点线所示,优化波形与图3b)中相应的波形类似,体现了有色高斯噪声背景下最大化互信息的优化波形的特点。随着Ith下降到一定程度,如图3d)中橙色加号线所示,波形既体现出一定的目标匹配特征,同时其大致的轮廓又与OP2相似,说明此时的波形是图3b)与图3c)中相应波形的组合。当Ith的值继续降到更低时,如图3d)中紫色叉号线所示,优化波形与图3c)中相应的波形类似,体现了有色高斯噪声背景下最小化KL距离的优化波形的特点。当Ith≤0.073 7时,优化波形与OP2一致。
为了更直观地体现雷达和截获接收机在优化过程中性能的变化,针对多个不同的约束条件计算了雷达和截获接收机的信噪比损失量,如图4所示。随着互信息约束的值越来越小,截获接收机和雷达都将损失一定量的信噪比,但截获接收机的信噪比损失更为严重。这说明该方法可以很好地完成以少量的雷达任务性能损失极大地削弱截获接收机性能的波形设计。直到互信息的约束下降到一定程度时,雷达和截获接收机的信噪比损失达到最大,且其性能损失差距也达到最大,说明优化波形具有优越的LPI性能。



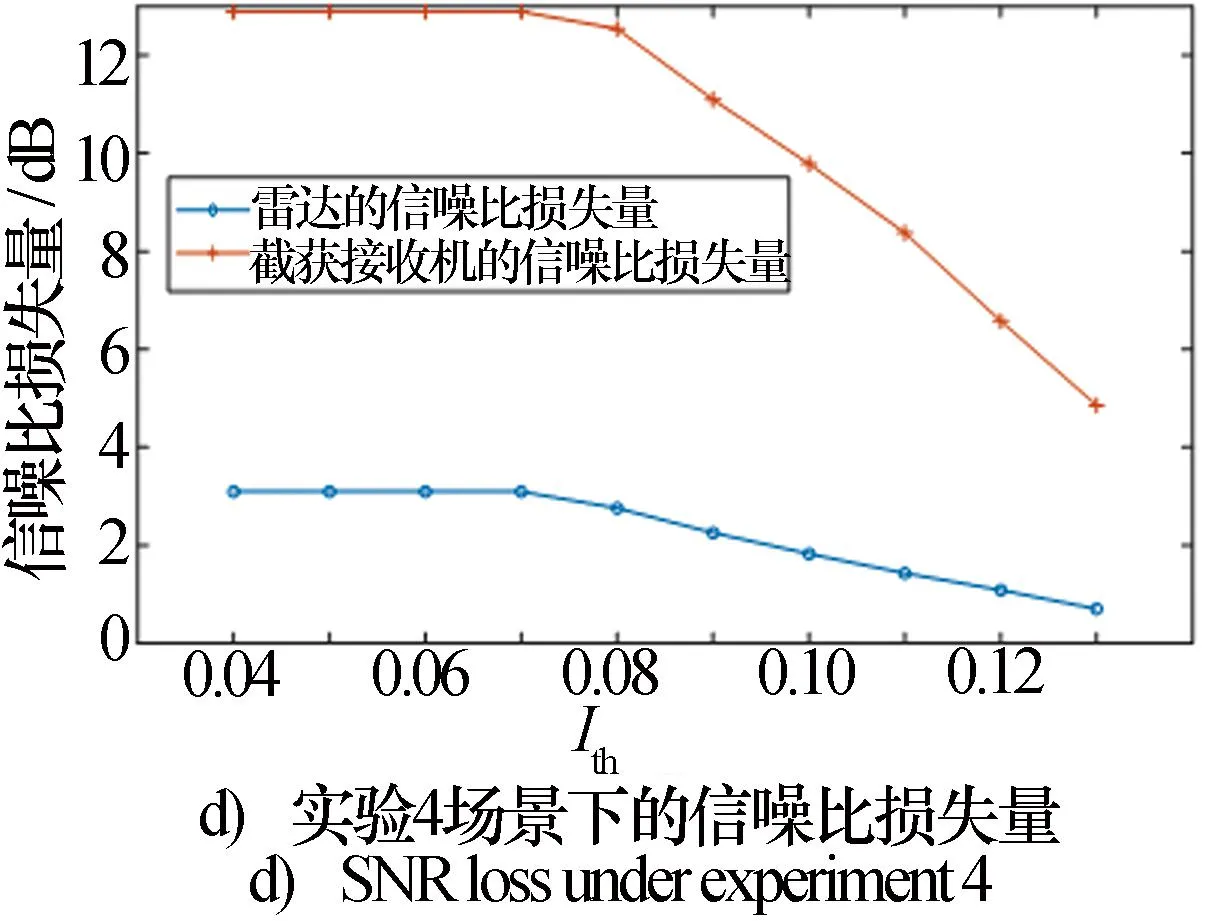
图4 雷达和截获接收机性能衰减随Ith的变化曲线Fig.4 Radar and intercept receiver performance degradation curve with Ith
从表3可以看出,本节所优化波形的雷达信噪比损失量约为3 dB,小于与之相比的任何一种LPI波形,即对雷达的性能影响最小。截获接收机损失的信噪比相较于LFM波形高出许多,与其他常见的LPI波形相比也十分接近。与文献[7]所使用的传统优化算法相比,在针对仅最大化雷达任务性能的优化问题中,本文优化波形的最大峰值较低,峰的个数较多,说明本文所用的算法更倾向于将功率在频域展开,而不是集中于某几个频点上,这对于设计LPI波形是有益的。当功率相同时,同一噪声背景下,最小化KL距离的波形设计的结果与文献[7]是一致的。由上述分析可知,与传统优化算法相比,本文所提方法省去了复杂的推导过程和辅助条件,且不依赖初始值的选取,设计出了具有良好LPI性能的发射波形。
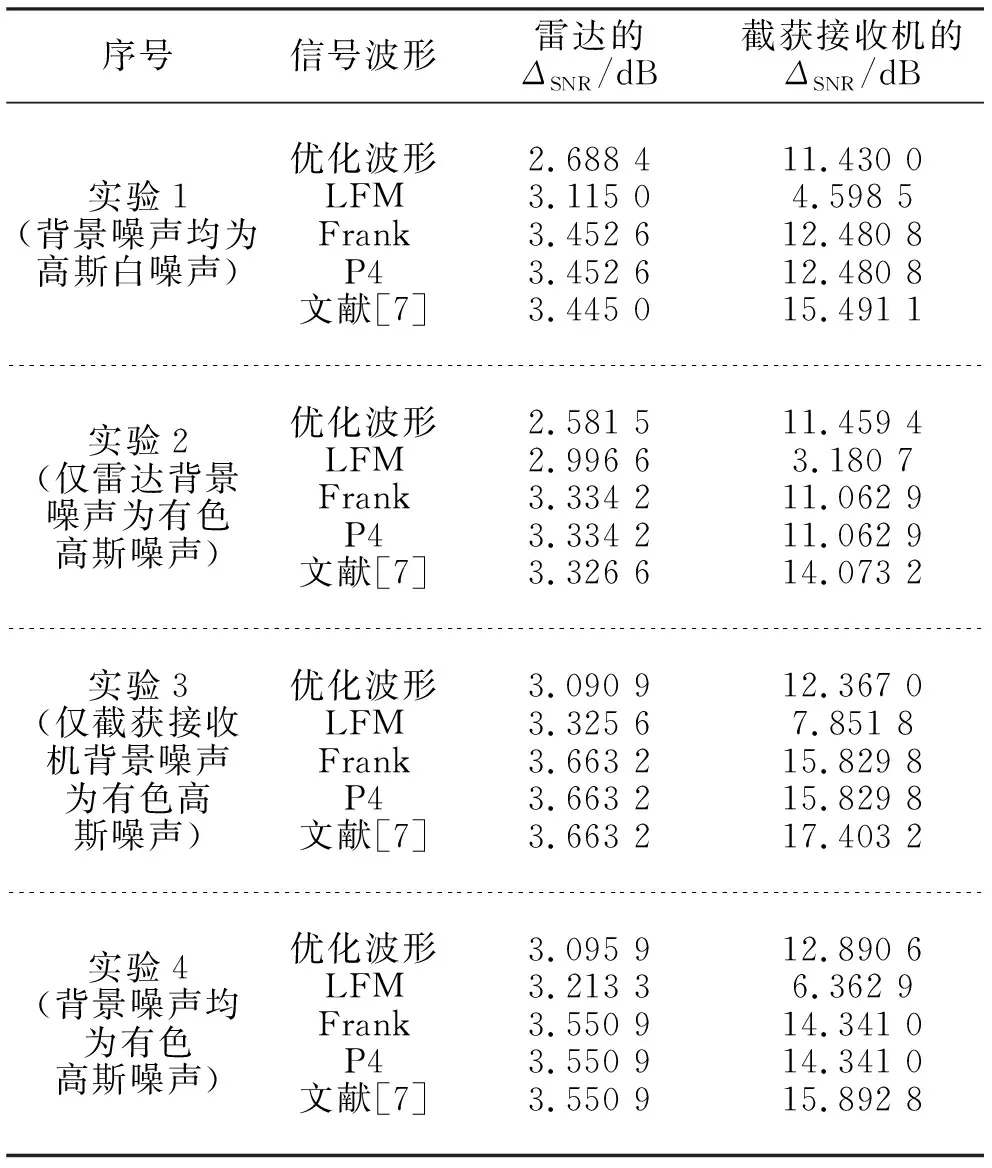
表3 优化波形的信噪比损失量对比Tab.3 Comparison of the loss of signal-to-noise ratio of optimized waveforms
4 结束语
本文以实现雷达低截获性能为目标,设计出可以根据任务要求和环境信息进行调整的LPI波形。考虑到传统优化算法应用于复杂、困难的优化问题时有较大的局限性,提出将基于种群的Jaya算法结合罚函数应用于波形优化问题的求解。所提方法避免了传统优化算法对拉格朗日乘子的复杂求解以及初始值选取不当导致局部优化,为基于信息论的波形设计问题提供了一种更加简单高效的求解方式。通过仿真验证了所优化的波形能够以较小雷达的性能损失,获得良好的低截获性能。
