拼宽路基水泥搅拌桩加固方案有限元分析方法及应用

王俊伟，曹强强

（中交一航局第二工程有限公司，山东 青岛 266071）

0 引言

为最大限度地利用土地资源，高速公路改扩建工程一般采用在原高速公路边坡上拼宽的方案，但该类方案面临路基沉降难以控制和整体稳定性较差的问题，原有路基经过多年运营，沉降已基本完成，老路边坡上新填方和交通荷载必然引起老路基附加沉降，且新老路基之间极易产生不均匀沉降病害[1]，新路基与老路基拼宽部位如何保证紧密衔接形成整体是高速公路改扩建工程的关键。目前，路基拼宽部位采取的工程措施[2-4]主要包括：老路基边坡削坡，老路基边坡开挖台阶，沿路基纵向铺设土工格栅等。在工程实践中，路基拓宽往往面临水渠鱼塘、软土地基[5]、熔岩采空区等各种不利水文地质条件，常规处治措施难以满足建设标准要求，为此需因地制宜采用拓宽路基加固措施。

本工程在既有湖堤大道基础上扩建为双向四车道一级路，工程建设重难点为：改扩建道路不均匀沉降及湖堤滩涂软弱土地基、高地下水位、路堤一侧鱼塘积水等，为此设计采用不同桩长的水泥搅拌桩对原有路堤及新建路基下卧软土地基进行加固，搅拌桩作为常用复合地基的一种常见形式，在软土地基加固处理中已经成熟应用，而在这类湖堤拓宽道路中的加固效果尤其是差异沉降控制作用方面还有待进一步明晰。为此本文针对工程设计方案，开展数值仿真计算，旨在通过模拟全施工过程中沉降、水平位移与稳定性等关键参数的变化规律，揭示该处治方案的有效性，并通过数据分析对方案进行优化改进，为今后类似工程提供参考。

1 工程概况

环湖大道东线全长116.2 km，其中环湖大道K2+500—K3+700、K4+300—K5+800 段按堤外加宽方式进行设计，因堤顶第2 层弱膨胀性黏土厚度较大，实施难度较大。故路基处理拟采用水泥搅拌桩改良此类不良土质的方案。路段路基清表主要位于湖滩内侧滩地，因存在多年淤积土，清表厚度按30 cm 计。当原地面纵坡大于12%或横坡陡于1∶5 时，进行挖台阶处理，台阶宽度应大于2 m，并设置成向内大于4%的坡度。

翻挖原湖堤厚1.40 m（路面结构60 cm+路床处理厚度80 cm）后，沿新旧堤相接的边坡线开挖三级台阶，分别在老堤堤顶开挖面、边坡上的台阶、加宽侧的湖滩共计4 个平台采用水泥搅拌桩法处理，再采用素土逐层回填，然后采用分层冲击碾压处理。原湖堤路基水泥搅拌桩桩长7 m，新建路基基底水泥搅拌桩桩长10 m，等边三角形布置，间距2 m，桩径0.5 m，经处理后的路基填土4.5 m，路基顶宽28.5 m，边坡坡率为1∶3。湖堤路基改扩建设计如图1 所示。

图1 湖堤路基改扩建设计图（cm）Fig.1 Design drawing for subgrade reconstructing and widening of Hudi Avenue（cm）

2 有限元分析模型

路基属于长条基础，交通荷载与自重作用下产生的表面纵向应力波可视为均匀分布，沿路基纵向结构内部变形与应力分布规律基本相似，因此可采用平面应变模型仿真路基状态，基于平面应变原理建立的二维仿真模型[6]基本假定有：

1） 土体为弹性材料，采用Mohr-Coulomb 模型；

2） 路基和地基的初始应力场由自重荷载产生；

3） 路基采用水泥搅拌桩加固，桩土接触条件为部分滑动，接触界面用滑移系数模拟；

4） 地基左右边界不透水，底部和上部为透水边界；底部完全固定约束，两侧竖直边界施加滑动约束。

考虑计算精度与有效计算，模拟地基土深度至地表以下20 m，模型如图2 所示。

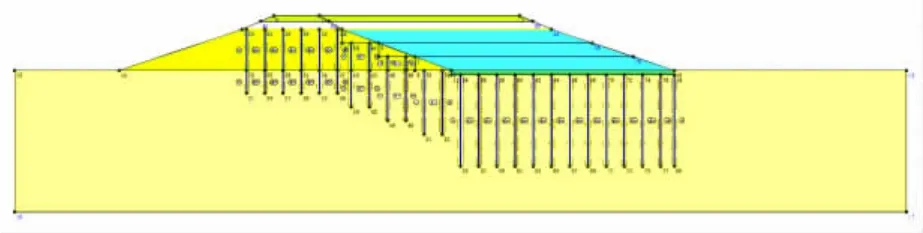
图2 有限元计算模型Fig.2 Finite element calculation model

有限元软件在平面问题计算中有2 种模式可用以模拟水泥搅拌桩，实体单元或Plate 单元。考虑设计计算中重点关注路基整体沉降分布以及水泥搅拌桩受剪作用，且桩间距密集，桩土变形基本协调，因此，本文采用Plate 单元模拟水泥搅拌桩。其中，桩Plate 单元的属性及桩的属性需根据桩间距布置，并进行平面应变参数换算。桩的平面应变等效涉及桩体刚度和地基渗透系数。刚性桩本身较为致密，渗透系数小，因此，主要考虑刚度等效问题。本文采用的刚度等效计算方法假设桩与桩间土加权平均刚度等于条形板刚度，条形板长度等于相邻两桩中心点距离，如图3 所示。

图3 桩刚度等效Fig.3 Equivalent stiffness of pile

根据土工勘察以及相关室内试验得到土体物理力学参数，见表1。

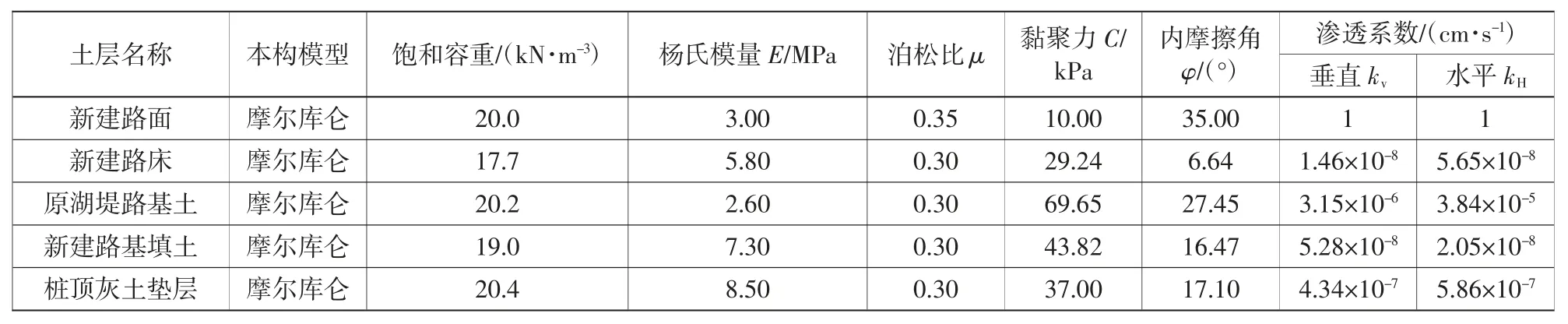
表1 土体主要参数指标Table 1 Main parameters and indicators of soil

全局网格划分疏密度设为粗糙，桩土接触范围及桩端局部位置2 次加密。桩周网格精细程度的参数是接触面的长度。有研究认为宜采用有厚度尽量小的接触面单元，而本文采用的Plaxis 默认Goodman 单元是无厚度单元，但有一个Virtural thickness factor 的参数，默认为0.1。如这个默认值不改动，则虚拟厚度为单元尺寸的0.1 倍，接触面的厚度不仅取决于单元的长度，还要考虑整个结构的接触长度及估算可能发生的相对错动。与桩接触的土层，需要输入折减系数Rinter，Rinter需根据桩的实际表面积与模拟表面积相等的条件（平面应变问题导致的）进行换算。有限元软件手册中建议的数值为0.67。桩结构周圈的回填材料由于垂直于图2 模型的纸面方向，且桩体较长，平面问题成立，因此可取为0.67。

根据施工情况，分别计算既有线运营情况下土体振动响应，考虑为表2 中序号为2、4、5、6的4 种工况。

为明确该设计方案控沉效果[7]，本次计算考虑投入运营后路基受力变形计算，为此模拟交通荷载作用下路基响应。交通荷载的模拟遵循以下原则：将车辆按最不利情况排列，将车辆的设计荷载换算成当量土柱高（即以相等压力土层厚度来代替荷载），以h0表示。

把行车荷载换算成条形柱高度，换算公式为：

式中：N为横向分布的车辆数，单车道N=1，双车道N=2，布置4 辆车；Q为每一辆车的重量，取小客车，单车重300 kN；γ 为路基填料的容重，取20 kN/m3；L为汽车前后轴的总距，小客车取3.8 m；B为横向分布车辆轮胎最外缘之间总距，B=Nb+（N-1）d；其中b为每一车辆的轮胎外缘之间的距离1.8 m；d为相邻车辆轮胎最外缘之间的距离1.3 m。

行车荷载换算为相应的土柱，由式（1）得h0=1.422 m，车辆按最不利情况排列（4 辆车）时计算出B=11.1 m，即最不利交通荷载换算土柱尺寸，宽11.1 m，高1.422 m。

3 结果及分析

3.1 沉降变形分布变化规律

计算选取A、B、C3 个监测点，分别为新老路基拼宽结合部原路堤坡脚、新老路基拼宽结合部路床底部、新老路基拼宽结合部新建路基坡脚，如图4 所示。

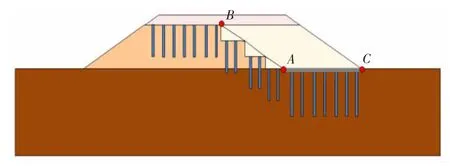
图4 计算监测点布设示意图Fig.4 Schematic diagram of calculation and monitoring point layout

计算得到施工全过程及运营360 d 以后，沉降-时间变化曲线及湖堤拓宽道路沉降分布云图如图5、图6 所示，可见拓宽湖堤路基投入运营后，在交通荷载及自重应力作用下，沉降最大值分布于新老路基拼宽结合部，这与理论计算、工程实践吻合，新老路基在荷载引起的附加应力作用下重新发生固结变形，沉降最大值0.47 m。

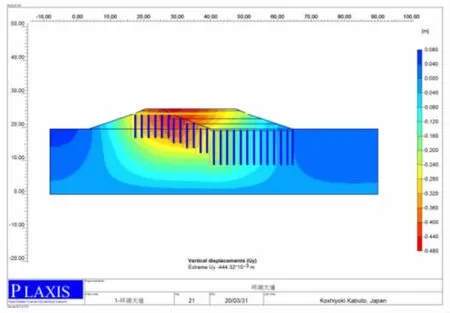
图6 沉降分布云图Fig.6 Settlement distribution cloud map

由竖向位移增量（dUy）云图可知软土路基不同深度土层在分级填筑荷载下土体竖向变形发展趋势。由图7 可知，路床中心底下土体位移增量较其同一深度处大，但当路堤填筑完毕填土高度达到4.5 m 时，路基拼宽区土体位移增量较大，表明路基的失效机制正沿该断面位移增量梯度变化凹点处的连线产生，同时也表明该连线处的土体已进入塑性发展区，对软土路基的安全造成极大的隐患。

3.2 水平位移分布变化规律

湖堤拓宽道路水平位移分布云图如图8 所示，可见最大水平位移发生在老路基开挖坡脚位置，位移方向为开挖路槽一侧，最大值12.6 cm。分析原因为，原湖堤路基开挖破坏了其应力状态[8]，新建路基土填筑产生的附加应力及路堤内水泥搅拌桩挤土造成该位置产生较大的水平位移，而新建路基坡脚由于水泥搅拌桩的加固作用，反而水平位移较小。

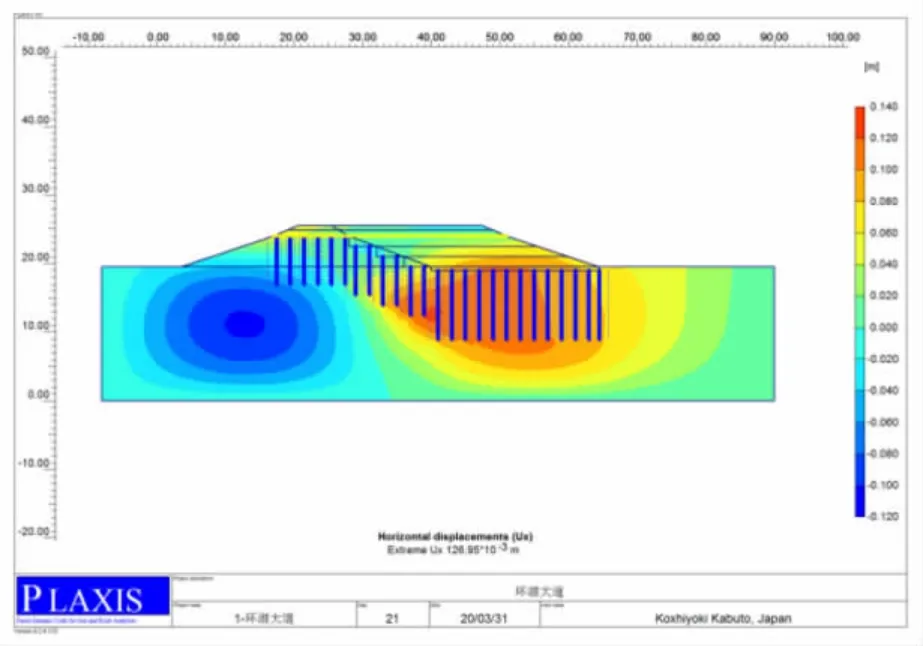
图8 水平位移分布云图Fig.8 Horizontal displacement distribution cloud map

3.3 路堤稳定性分析

本文采用强度折减法计算路堤安全系数，即计算中通过不断降低边坡的安全系数F，折减后的参数不断代入模型进行重复计算，直到模型达到极限发生破坏，此时发生破坏前的值就是边坡的安全系数。从模型输出结果，可以清楚地看到失效机制在第二计算工序之后开始发展。本模型计算强度参数的减小由总乘子∑Msf来控制，这个参数逐步增加直到破坏。假定在失效后连续几步的计算大体给出一个常值的∑Msf，即认定其为安全系数。图9 即为有限元强度折减法所得的∑Msf。

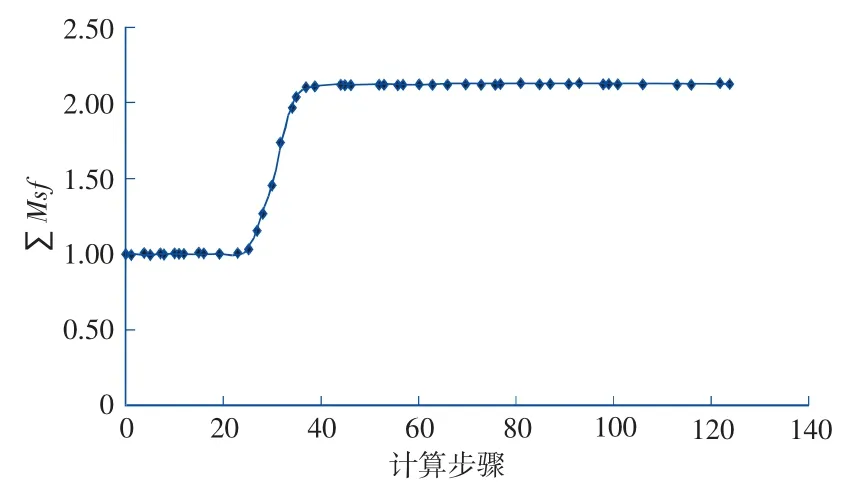
图9 强度折减法安全系数变化曲线Fig.9 Safety factor change curve of strength reduction method

由图9 可知，强度折减计算得到采用搅拌桩加固以后的拼宽路基安全系数2.2，有足够的安全储备，路基不会发生失稳破坏[9]。

3.4 路堤水泥搅拌桩受力分析

通过桩身剪力计算，可明确施工阶段及运营阶段水泥搅拌桩的受力工作机理，计算得到新老路基不同位置处的水泥搅拌桩的剪力分布图、弯矩分布图和轴力分布图如图10—图12 所示。

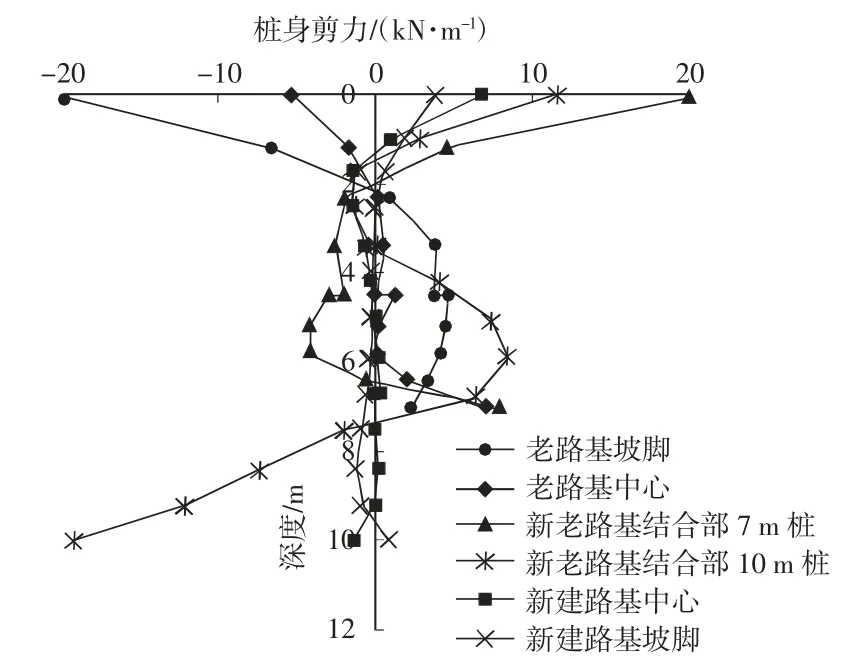
图10 不同位置桩身剪力分布图Fig.10 Shear force distribution diagram of pile shaft at different locations

路堤荷载下不同位置的水泥搅拌桩对维持路堤稳定的作用是不同的，由图10 可知，新老路基结合部水泥搅拌桩（10 m）桩身剪力最大，即其发挥了主要的抗剪作用，由图11 可知，新老路基结合部水泥搅拌桩（10 m）承受了最大的弯矩作用，该处的水泥搅拌桩阻断了新老路基结合部潜在滑动面的形成与贯通。

图11 不同位置桩身弯矩分布图Fig.11 Moment distribution diagram of pile shaft at different locations

桩身剪力与弯矩较大的为老路基坡脚处水泥搅拌桩，原因分析为老路基开挖后形成一侧临空面，在上部交通荷载作用下对路基坡脚产生较大的推力，潜在的滑动剪切破坏给老路基带来失稳破坏的隐患。

由图12 可知，除新老路基结合部水泥搅拌桩（10 m）外，桩身轴力较大的则是新老路基结合部搅拌桩（7 m）与新建路基中心处搅拌桩，反映新建路基部位主要对地基产生垂直向下荷载。

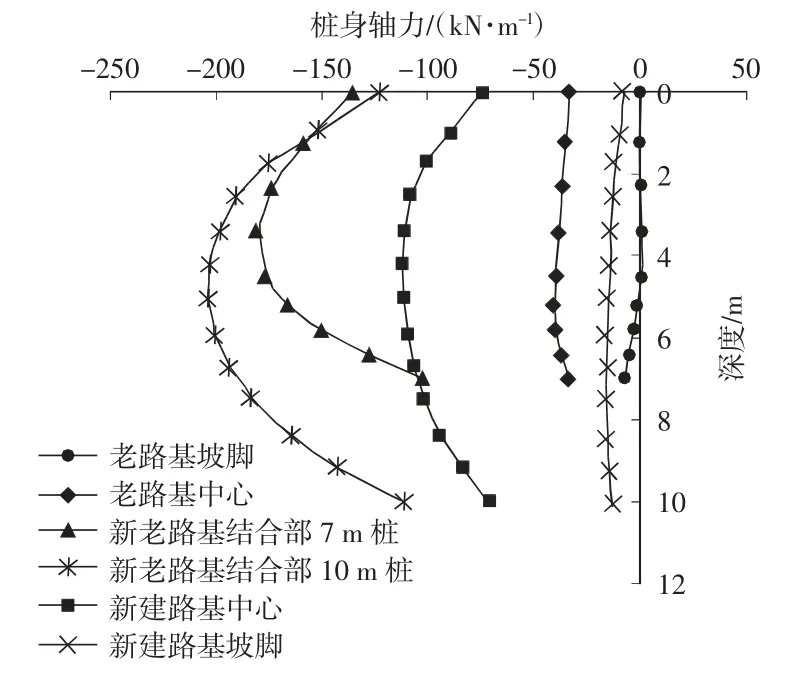
图12 不同位置桩体轴力分布图Fig.12 Axial force distribution diagram of pile shaft at different locations

4 结语

针对既有道路改扩建工程中不均匀沉降控制难以及地质条件复杂等问题，设计采用不同桩长的水泥搅拌桩对原有路堤及新建路基下卧软土地基进行加固，通过数值仿真计算，模拟全施工过程中沉降、水平位移与稳定性等关键参数的变化及分布规律并验证于湖堤大道改扩建工程，主要得到以下结论：

1） 路基下部软弱土地基的加固效果，受水泥搅拌桩的深度影响显著，深度不足将致使拼宽区基底土体进入塑性发展区，设计时需重点考虑水泥搅拌桩的深度这一参数。

2） 经水泥搅拌桩加固的改扩建路基，采用强度折减法计算得到安全系数2.2，与常规填方路基设计要求的1.35 相比，具有足够的安全储备。

3） 不同位置的水泥搅拌桩承担的主要功能不一致，新老路基结合部及老路基坡脚处水泥搅拌桩主要承担抗剪、抗弯作用，新建路基水泥搅拌桩主要承受了来自上部填土的垂直荷载作用。