不同粒径纳米二氧化硅对三元乙丙橡胶性能影响的分子动力学模拟
2024-03-29韩晓莹王泽鹏李鑫炎
韩晓莹,王泽鹏,李鑫炎
(青岛科技大学 机电工程学院,山东 青岛 266061)
三元乙丙橡胶(EPDM)因具备耐老化、电绝缘和耐腐蚀等优良性能,已被广泛应用于电线电缆、汽车配件和密封材料等领域[1],但随着应用环境越来越复杂,市场对EPDM复合材料的性能也有了更严苛的要求。
二氧化硅(SiO2)俗称白炭黑,是一种无毒无味的非金属材料[2],可作为EPDM的补强剂。谢庆等[3]建立了纳米SiO2/环氧树脂复合材料模型,发现纳米SiO2的掺杂使环氧树脂复合材料的内聚能密度明显增大,自由体积分数有不同程度减小。E.Q.HE等[4]建立了纳米SiO2/橡胶复合材料模型,结果表明纳米SiO2粒子的引入使复合材料的弹性模量增大约190%。X.S.LIU等[5]研究了在分子尺度上添加纳米SiO2以提高丁腈橡胶(NBR)复合材料的力学和摩擦学性能的作用机理,结果表明纳米SiO2与NBR分子链之间的氢键和界面相互作用减小了NBR复合材料的自由体积分数,使复合材料的剪切模量比纯NBR增大了25%。Y.J.WANG等[6]通过分析EPDM复合材料的自由体积和扩散系数等参数,研究了温度、应变和应力对EPDM复合材料自由体积的影响,估测其防水性能。张鹏宇等[7]将不同粒径的纳米SiO2填加到天然橡胶(NR)中制备纳米SiO2/NR复合材料,发现随着纳米SiO2粒径的增大,复合材料的拉伸强度增大。
目前主要对常压常温条件下纳米SiO2/EPDM复合材料的性能进行研究,对高压低温条件下的性能研究较少。本工作以EPDM为基体,以纳米SiO2为补强剂,基于分子动力学方法建立纳米SiO2/EPDM复合材料模型,分析在高压低温条件下纳米SiO2粒径对纳米SiO2/EPDM复合材料微观结构和性能的影响。
1 模型构建及优化
1.1 模型构建
采用Materials Studio 9.0软件构建EPDM分子的单体模型(见图1)和球形纳米SiO2的结构模型(见图2)。其中,EPDM分子由物质的量质量分数分别为70%的乙烯、25%的丙烯和5%的亚乙基降冰片烯组成。王奥[8]在研究中发现,当聚合物分子链的聚合度大于50时,模型的密度计算结果趋于稳定,因此构建的EPDM分子链的聚合度为60。

图1 EPDM分子单体模型Fig.1 Monomer models of EPDM molecule
图2 纳米SiO2的结构模型Fig.2 Structural model of nano-SiO2
EPDM模型和纳米SiO2/EPDM复合材料模型如图3所示。将EPDM模型记为1#模型,纳米SiO2粒径为1.2,1.5,1.8和2.0 nm的纳米SiO2/EPDM复合材料模型分别记为2#—5#模型。
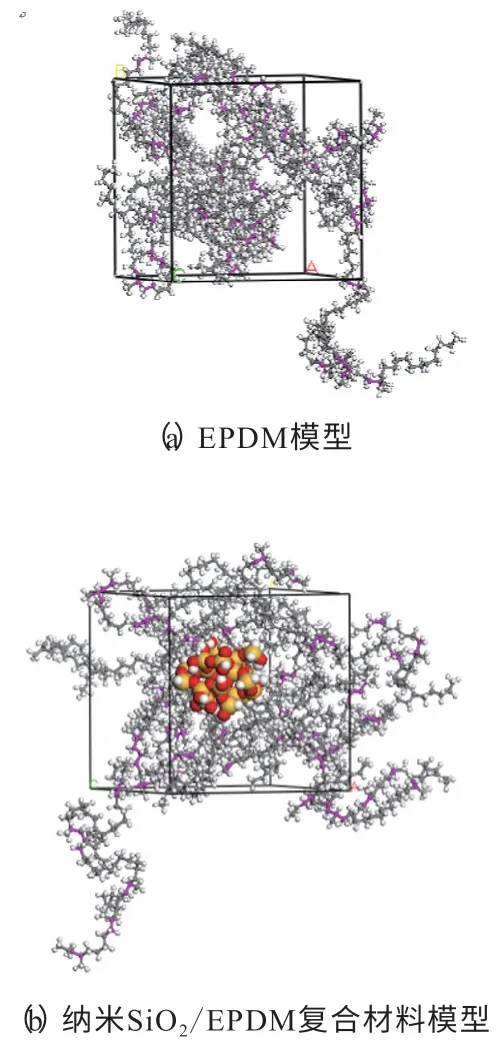
图3 EPDM模型和纳米SiO2/EPDM复合材料模型Fig.3 EPDM model and nano-SiO2/EPDM composite model
1.2 模型优化
对纳米SiO2/EPDM复合材料模型进行分子动力学处理,模型的初始密度为0.8 Mg·m-3,保持2#—5#模型中纳米SiO2的质量分数一致[9-11]。优化计算在COMPASS力场下进行,均采用Smart算法,能量收敛于4.19×10-4kJ·mol-1,力收敛于2.09×10-2kJ·(mol·Å)-1。对优化后的此结构进行300~500 K的5个退火循环。在此基础上,进一步放松结构,温度设置为298 K,依次进行1×10-9s的等温等体积(NVT)和等温等压(NPT)系综的动力学平衡,以此找到模型系统的能量最低构象。本工作分子动力学过程中均采用Anderson控温和Berendsen控压,时间步长选择1×10-15s。
分子动力学模拟过程中纳米SiO2/EPDM复合材料模型的密度-时间曲线如图4所示。
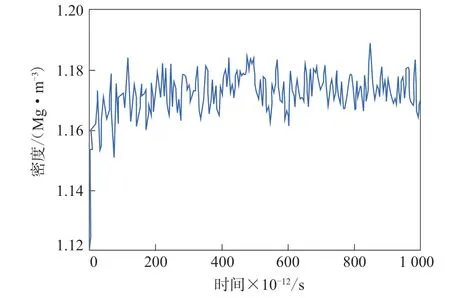
图4 纳米SiO2/EPDM复合材料模型的密度-时间曲线Fig.4 Density-time curve of nano-SiO2/EPDM composite model
从图4可以看出,随着时间的延长,纳米SiO2/EPDM复合材料模型的密度逐渐趋于稳定,这表明在分子动力学处理过程中找到了最低能量构象,模型最终达到平衡状态。
2 结果与讨论
2.1 玻璃化温度(Tg)
Tg是聚合物的特征参数,当温度低于Tg,橡胶分子链被冻结;当温度高于Tg,橡胶分子链开始运动,并表现出高弹性。因此,Tg越低,橡胶的耐低温性能越好,在低温下也可以表现出良好的弹性,具有不易结晶的特性。
Tg可以通过模型密度与温度的关系表征,常压条件下EPDM模型的密度-温度曲线如图5所示。
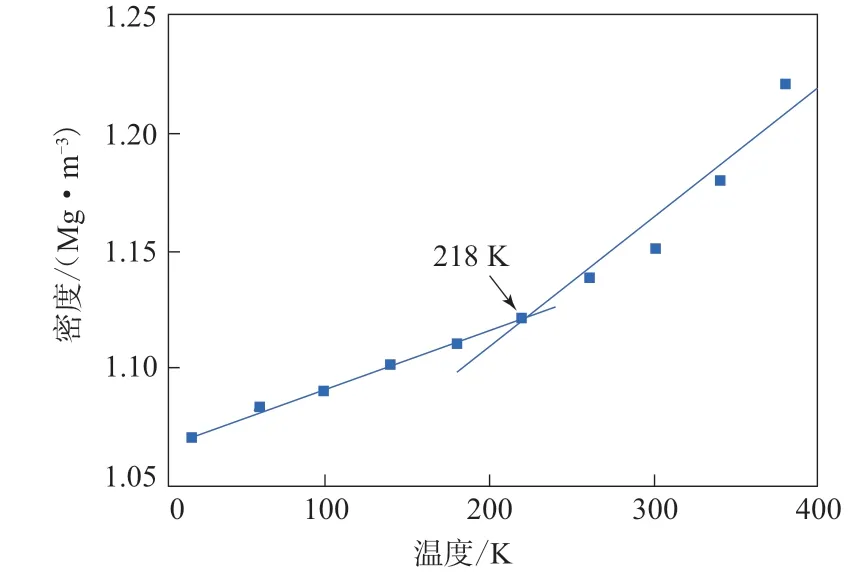
图5 EPDM模型的密度-温度曲线Fig.5 Density-temperature curve of EPDM model
从图5可以看出,常压条件下EPDM的Tg为218 K,与A.GUNGOR等[12-15]测得的结果相近,说明EPDM模型的模拟结果与试验结果基本一致,表明EPDM模型与实际相符。
在100 MPa和230 K条件下,同样用密度-温度的线性拟合得到EPDM模型和纳米SiO2/EPDM复合材料模型的Tg如图6所示。

图6 EPDM模型和纳米SiO2/EPDM复合材料模型的TgFig.6 Tg of EPDM model and nano-SiO2/EPDM composite models
从图6可以看出,与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的Tg都有不同程度地升高。这是因为纳米SiO2与EPDM发生反应,使EPDM分子链的运动能力减弱,从而使Tg升高,其中粒径为1.2 nm的纳米SiO2对复合材料Tg的提升作用最为明显,其Tg比EPDM的Tg高5 K。随着纳米SiO2粒径的增大,复合材料的Tg逐渐降低,但都高于EPDM。这是因为纳米SiO2的比表面积随着粒径的增大而减小,这也减小了纳米SiO2与EPDM的接触面积,降低了其结合强度,因而小粒径纳米SiO2更容易与EPDM结合,复合材料的结构更稳定。
2.2 均方位移(MSD)
MSD表示粒子移动距离与移动时间的关系,它可以表征橡胶的热稳定性[16-18]。MSD可以用式(1)计算:
式中,ri(t)和ri(0)分别为t时刻和0时刻的坐标。
100 MPa和240 K条件下EPDM和纳米SiO2/EPDM复合材料模型的MSD曲线如图7所示。

图7 EPDM模型和纳米SiO2/EPDM复合材料模型的MSD曲线Fig.7 MSD curves of EPDM model and nano-SiO2/EPDM composite models
从图7可以看出,与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的运动能力均减弱,且纳米SiO2的粒径越小,复合材料的运动能力越弱。这说明填充纳米SiO2可以使EPDM分子链的运动能力受到限制,有利于提高复合材料的稳定性。
2.3 自由体积分数(FFV)
自由体积是影响聚合物材料的重要参数之一,可以反映聚合物分子链的运动情况,自由体积存在,小分子才有运动的空间。FFV为自由体积占总体积的比例,FFV可以由式(2)计算:
式中,VF为自由体积,VO为占用体积,VT为总体积。
100 MPa和230 K条件下EPDM模型和纳米SiO2/EPDM复合材料模型的FFV如图8所示。

图8 EPDM模型和纳米SiO2/EPDM复合材料模型的FFVFig.8 FFV of EPDM model and nano-SiO2/EPDM composite models
由图8可以看出,与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的FFV均减小,且纳米SiO2的粒径减小,复合材料的FFV呈减小趋势。其中,纳米SiO2的粒径为1.2 nm时,复合材料的FFV最小,为11.85%,比EPDM的FFV减小1.09%。这是因为在EPDM中填充纳米SiO2会占据一定的空间,致使EPDM分子链的运动空间变小,从而减小FFV,而小粒径纳米SiO2的比表面积更大,与EPDM分子间的相互作用更强,会更大程度上限制EPDM分子链的运动。
2.4 内聚能密度(CED)
CED可以衡量EPDM分子链与纳米SiO2之间的相互作用力大小,CED越大,EPDM与纳米SiO2之间的相互作用力越大,二者结合越紧密,纳米SiO2/EPDM复合材料模型的结构越稳定[12-13],其CED的计算式如下:
式中,Ecoh是模型中EPDM分子链的内聚能,V是模型的体积,Einter是模型中EPDM分子链间的能量,Etotal是模型的总能量,Eintra是模型中EPDM分子链内的能量,< >代表模型在NPT系综下的平均值。
在100 MPa 和230 K 条件下计算得到1#—5#模型的CED 分别为237,299,296,288 和262 J·cm-3。可以看出,与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的CED均明显增大,且填充纳米SiO2的粒径越小,复合材料的CED越大,这与Tg的结论相对应,即模型的CED越大,Tg越高。
2.5 径向分布函数(RDF)
RDF[g(r)]可以反映给定粒子周围的其他粒子在此空间的分布概率,它是表征聚合物微观结构的重要参数之一[19]。
式中,nB为A粒子周围B粒子的数量,NB是B粒子的数量,r是给定粒子的半径。
100 MPa和230 K条件下EPDM模型和纳米SiO2/EPDM复合材料模型的全原子RDF图如图9所示。

图9 EPDM模型和纳米SiO2/EPDM复合材料模型的全原子RDF图Fig.9 All Atom RDF charts of EPDM model and nano-SiO2/EPDM composite models
由图9可以看出,EPDM模型与纳米SiO2/EPDM复合材料模型的全原子RDF图的区别在于,纳米SiO2/EPDM复合材料的全原子RDF图在r为0.095 nm附近出现第1个峰,此峰为纳米SiO2表面的—OH基团[如图10(a)所示]特征峰,这表明纳米SiO2参与到复合材料的反应中。EPDM与纳米SiO2/EPDM复合材料模型的其余峰均可对应:在r为0.110 nm处出现的峰为C—H[如图10(b)所示]特征峰,此处峰值较大,说明EPDM和纳米SiO2/EPDM复合材料存在大量的C—H键;在r为0.151 nm处出现的峰C—C键[如图10(c)所示]特征峰;在r为0.177 nm处出现的峰表征—CH3上2个H原子的间距[如图10(d)所示]。此外,在r小于0.09 nm的范围内没有峰且g(r)趋于0,这是因为存在范德华效应;在r大于0.4 nm的范围内也无峰且g(r)趋近于1,这是由于EPDM的无定型特征。
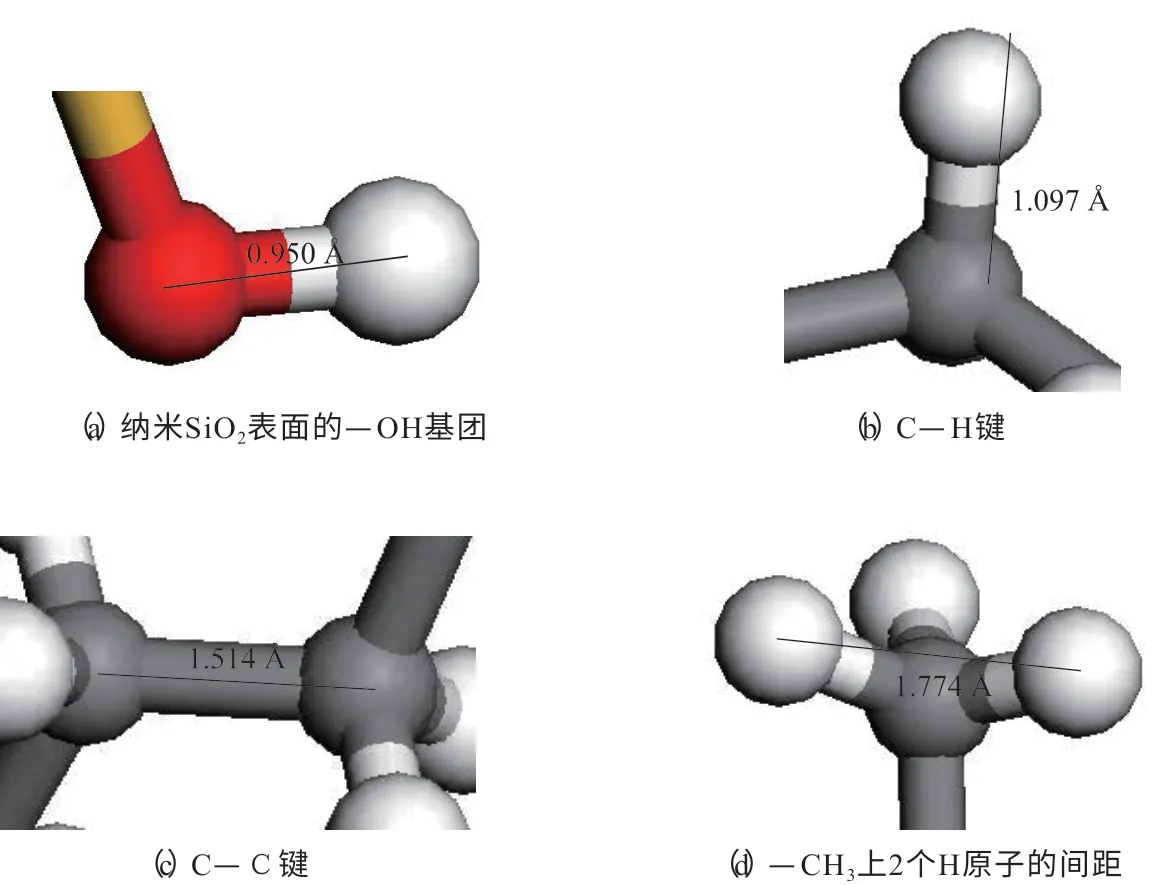
图10 模型局部结构Fig.10 Local structures of model
2.6 力学性能
在Materials Studio 9.0软件中,系统力学分析方法主要有3种:恒应变法、静态法和应力涨落法。本工作采用恒应变法,即对平衡体系施加一系列有限应变,从而得到与力学性能相关的参数。
EPDM模型和纳米SiO2/EPDM复合材料模型的刚性矩阵Cij如下式[20-22]:
式中,λ和μ为材料的弹性常数,λ表征材料的压缩性能,μ表征材料的剪切性能[23-24]。
λ可由刚性矩阵求得:
由λ和μ可以求得EPDM和纳米SiO2/EPDM复合材料的体积模量(K)、剪切模量(G)和弹性模量(E):
在100 MPa和230 K条件下对EPDM模型和纳米SiO2/EPDM复合材料模型进行恒应变法模拟,得到刚性矩阵,求得模型的模量,如图11所示。

图11 EPDM模型和纳米SiO2/EPDM复合材料模型的模量Fig.11 Moduli of EPDM model and nano-SiO2/EPDM composite models
由图11可以看出,与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的K,G和E均有不同程度的增大。其中,纳米SiO2粒径为1.2 nm时,复合材料的K增大5.98%,G增大198.00%,E增大34.65%;粒径为2.0 nm时,复合材料的K增大4.56%,G增大37.00%,E增大19.15%。由此可见,填充纳米SiO2可以增强材料的力学性能,且增强作用随纳米SiO2粒径的增大而减小。这是因为小粒径的纳米SiO2比表面积更大,与橡胶分子链的相互作用能力更强,能很好的支撑起材料,使其更不易发生形变,从而呈现更优的力学性能。
3 结论
运用分子动力学建立了EPDM模型和纳米SiO2/EPDM复合材料模型,研究高压低温(100 MPa和230 K)条件下填充不同粒径纳米SiO2对纳米SiO2/EPDM复合材料微观结构和力学性能的影响,通过参数求解和性能分析,得到以下结论。
(1)与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的Tg都有不同程度地升高,其中粒径为1.2 nm的纳米SiO2对复合材料Tg的提升作用最为明显,其复合材料的Tg比EPDM高5 K,且随着纳米SiO2粒径的增大,复合材料的Tg逐渐降低,但都高于EPDM。
(2)填充不同粒径的纳米SiO2可使纳米SiO2/EPDM复合材料的微观结构发生改变,MSD和FFV都有所减小,减幅随纳米SiO2粒径的减小而增大;CED均有所增大,增幅随纳米SiO2粒径的减小而增大。纳米SiO2粒径对复合材料的全原子RDF影响不大。
(3)与EPDM相比,填充不同粒径纳米SiO2的纳米SiO2/EPDM复合材料的力学性能提高,提高幅度随纳米SiO2粒径的增大而减小,纳米SiO2粒径为1.2 nm时,复合材料的K增大5.98%,G增大198%,E增大34.65%。
