基于混合特征双重衍生和误差修正的风电功率超短期预测

袁 畅，王 森，孙永辉，武云逸，谢东亮

（1.河海大学能源与电气学院,江苏省南京市 210098；

2.南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省南京市 211106）

0 引言

随着环境问题日益凸显和能源需求不断增长,发展以风电为代表的新能源已成为全球趋势。截至2022 年底,全球风电累计装机容量为906 GW［1-3］,同比增长9%。但风电出力具有随机性和波动性,大量并入电网会导致发用电平衡难度加大［4-8］。因此,需要提高风电功率预测精度,建立可靠性高的风电功率预测模型［9］。

目前,风电预测精度的提高主要依靠特征工程和预测误差分析［10-11］。特征工程是指从原始数据中提取并构建有助于模型预测的特征的过程。文献［12］利用K-均值算法将不同风电场的集群划分为趋势相近的子集群,可有效提升预测精度。文献［13］利用模糊C均值聚类方法对功率输出特性类似的风机进行分类,降低预测的复杂度。但当数据量较小时,聚类算法难以确定合适的聚类中心和边界。也有学者提出基于数据降维、小波分解和粗糙集等数据分析算法进行特征处理［14-18］,但当特征稀疏时,会过度优化训练数据,导致模型过拟合。近年来,风电及相关领域专业知识的特征工程方法引起了广泛关注。文献［19］通过整合风电场的历史功率、数值天气预报和风电机组运行状态等数据构建风电功率预测模型,实现在不同时间尺度上的精准风电功率预测。文献［20］将海上风电机组时空特性与波动过程关联,构建精度更高的功率预测模型。但这些方法对数据依赖严重,面对数据种类少且特征稀疏的情况时,难以有效开展。

在风电功率预测误差分析方面,目前研究集中在预测结果的置信区间和预测的不确定性量度,进而提高预测模型的鲁棒性。文献［7］根据风电功率预测误差概率密度特性对误差进行分层来减小预测误差。文献［21］通过设计相应风电功率修正方法和预测误差分布的估计方法来提高预测精度。但以上误差分析算法都基于对误差分布的假设和先验,而对于未知的风电数据,误差分布的真实情况往往难以确定。文献［22］将误差以风速大小分类,并针对每类误差分别训练误差预测模型。但误差分布与风速未有显著的关联性,预测的误差精度较低。因此,需要开发一种误差修正策略,不依赖于误差的分布,直接从风电预测数据中挖掘误差的潜在规律,提高误差修正的鲁棒性和适应性。

按时间尺度,风电功率预测可分为超短期预测、短期预测和中长期预测。超短期预测的时间尺度为4 h,主要用于解决实时调度问题；短期预测的时间尺度为72 h,主要用于安排常规机组发电计划；中长期风电功率预测时间尺度为数星期或数月,主要用于新风电项目的可行性研究。超短期预测是这3 种时间尺度中非常关键且应用频繁的,实现超短期尺度精确预测尤为关键。

数值天气预报对于超短期预测非常重要,但目前一些风电场未配置高精度的数值天气预报系统,且缺乏自身历史气象情况的详细数据。因此,迫切需要一种不依赖于数值天气预报的风电功率预测方法。针对上述问题,本文提出基于混合特征双重衍生和误差修正的风电功率超短期预测方法。通过在原始特征中施加混沌噪声,并基于改进免疫算法（immune algorithm,IA）,实现大规模的特征衍生；设计误差修正模块并挖掘预测模型潜力,进而有效提升预测精度。

1 特征衍生

本文提出一种混合特征双重衍生方法,旨在改善数据不充分和特征稀缺的训练环境。首先,通过对原始特征中施加混沌噪声,得到基于混沌噪声扰动的衍生特征集,使特征表示具有更高复杂度。然后,以S-expression 形式作为抗体编码方案,并以IA作为特征寻优策略,构建基于IA 的特征衍生模型,实现大规模衍生特征,同时保证衍生特征的质量。

设数据集中的特征X=[X1,X2,…,Xl],其中,l为特征的数量。原始特征中仅有一列时间特征T,即原始特征X=[T],T=[T1,T2,…,Tt,…,Tn],其中,Tt为时间特征在t时刻的数值,n为数据长度。数据集中的标签y=[y1,y2,…,yt,…,yn]。原始预测标签为风电功率输出数值,即yt为t时刻的风电功率输出数值。为方便表述算法过程,定义Xtrain为训练集特征,Xtest为测试集特征,ytrain为训练集标签,ytest为测试集标签,Dtrain为训练集,Dtest为测试集。

本文定义的训练集中包含了传统意义上的训练集和验证集,有效避免了数据泄露,即在训练模型时,会将训练集Dtrain拆分为训练集和验证集,测试集不参与任何模型训练过程。

1.1 基于混沌噪声的特征衍生模型

由于原始数据特征的稀缺,特征表示同质化严重,导致预测模型无法完整地捕捉特征与预测标签之间的复杂非线性关系。本文使用混沌噪声扰动原有特征,将扰动后的数据生成新的特征,使特征的表示更加多样化和复杂化,实现特征的衍生。

混沌噪声是一种非线性、不可预测的随机过程,通常具有分形特征和频谱连续性。本文采用Lorenz混沌系统生成混沌噪声,Lorenz 混沌系统的方程为：

式中：σ、ρ、β为超参数；x、y、z为随时间变化的状态变量。

求解上述微分方程,并将状态变量x作为生成的混沌噪声信号。将生成的混沌噪声信号扰动原始特征数据X,生成多组混杂了混沌噪声的新特征X：

式中：h为衍生特征的数目。

基于混沌噪声衍生后的特征集具有更高复杂度,能够更好地反映和预测目标变量,从而有助于模型更准确地捕捉特征和目标变量之间的非线性关系。另一方面,加入混沌噪声可以提高模型的泛化能力,使其能够更好地适应其他未知数据,帮助减少模型的过拟合,使模型更具鲁棒性和泛化能力。

1.2 基于IA 的特征衍生模型

传统的特征衍生方法存在两种不足：1）缺少先验知识或经验规则时,难以有效地计算出大量新特征；2）新特征与预测目标的相关性不强,有效性待验证。

针对上述问题,本文提出一种基于IA 的特征衍生方法,通过随机化生成大量特征组合方式,增加优质特征的数量。通过定义相关性系数为目标函数,采用IA 优化出最佳的特征组合,保证构造的新特征均与预测标签高度相关。基于IA 实现特征衍生的相关流程概述如下。

步骤1：定义目标函数G为最大化Spearman 相关性系数的绝对值。

式中：X表示组合的第k条训练集特征的第i条数值表示组合的第k条训练集特征的平均值；为ytrain中的第i条数 值；yˉtrain为ytrain中所有数值的平均值。算法优化的目标是构造与预测标签有强相关性的特征,且相关性越强越好。

步骤2：随机生成维数为M的N个抗体,维数M与输入特征的数量相同,N为超参数,需要人为设置。

本文利用列表表达式,将带符号的公式编码成IA 中的抗体。每条抗体都表示用运算符和现有特征构建的一种新特征的计算公式。

首先,将公式转换成列表表达式中的Sexpression 形式［22］。使用S-expression 形式的编码方式可避免运算符优先级和结合性造成的误差,也便于交叉、变异等结构化操作。其次,将上述Sexpression 编码为列表,代表一条抗体。例如,对于随机生成的公式0.5(0.1x+y)+0.2,首先需要将其转 化 为 S-expression 的 形 式 (+(×0.5(+(×0.1x)y))0.2),然后编码为抗体{add,mul,0.5,add,mul,0.1,x,y,0.2}。

步骤3：计算激励度。

IA 以激励度函数作为选择依据,激励度函数可视为亲和度函数和浓度函数的结合。亲和度函数aff(kp,kq)为：

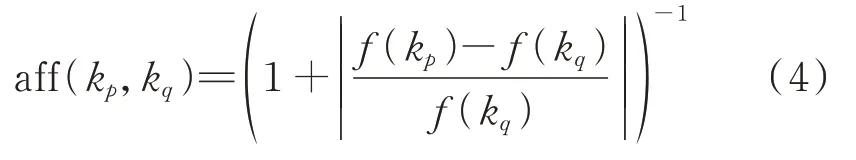
式中：kp和kq分别表示种群中的第p条和第q条抗体；f(kp)和f(kq)分别为kp和kq的适应度。

由于优化目标为目标函数最大化,适应度函数f和式（3）的目标函数相同,即此时式（3）中的X表示基于第k个抗体代表的公式所组合出的新特征的第i条数值,表示第k个抗体代表的公式所组合出的新特征平均值。

浓度函数den(kp)反映了一定区域内包含的抗体数量,其表达式为：

式中：S(kp,kq)为kp和kq之间的相似度；δ为相似度阈值,用于比较两个抗体相似度的数值。当两个解决方案之间的相似度超过这个阈值时,其中一个会被删除或减少,以保持整体解决方案集的多样性。相似度阈值δ［23］一般设定为0.9。

抗体的激励度sim(kp)是评估抗体的综合指标,需给予亲和度高且浓度低的抗体更多的激励度,可表示为：

式中：a和b为权重参数。

步骤4：将种群中抗体按激励度函数的大小排列,选择一定数量的抗体进行克隆。在抗体进行克隆之后,将克隆体进行交叉变异。

步骤5：交叉变异的过程与遗传算法中的交叉变异机制相似,但此时的抗体由S-expression 组成,无法用常规编码（如二进制编码等）的抗体直接进行加减乘除计算。交叉、变异过程如图1 所示。

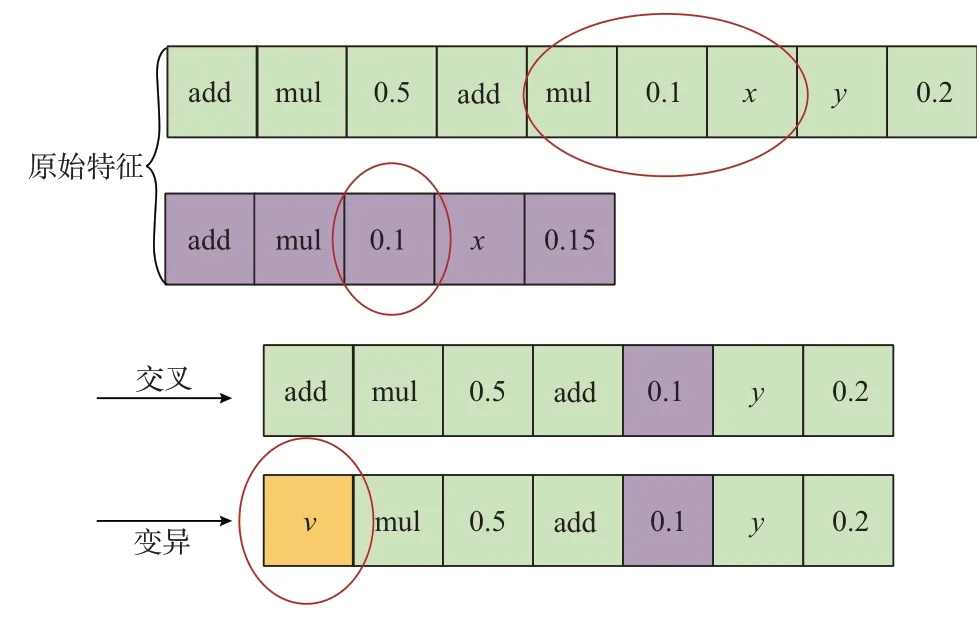
图1 交叉、变异过程说明图Fig.1 Diagram of crossover and mutation process

1）随机挑选两条抗体。从抗体集合A中随机抽取两条抗体,记为kp和kq。以抗体kp={add,mul,0.1,x,0.15} 与kq={add,mul,0.5,add,mul,0.1,x,y,0.2} 为例,分别对应0.1x+0.5 与0.5(0.1x+y)+0.2。

2）随机挑选kp和kq子集,交换子集得到新的抗体Kg。以kp的子集{mul,0.1,x}和kq的子集{0.1}为例,交换这两个子集,得到新抗体kg={add,mul,0.5,add,0.1,y,0.2},对应0.5+0.1y+0.2。

3）随机选择kg的一个节点,将其替换为一个随机的运算符、特征或数值,得到新的抗体km。以kg中的add 为例,替换为变量v,则新抗体km={v,mul,0.5,add,0.1,y,0.2},对应v(0.5+0.1y)。

步骤6：交叉变异后,从克隆抗体中选出最优抗体,放入下一代种群。然后,随机产生其余抗体,不断迭代重复,直至达到预设的迭代次数,筛选出最佳的q条抗体,作为新的特征。记完成特征衍生后的训练特征为。

步骤7：将Xtest使用上述的q条最佳抗体所代表的公式进行相同的特征变换,记完成特征衍生后的测试特征为。通过IA 计算出的最佳特征变换公式是基于训练集数据的。因此,未出现数据泄露。

2 改进的风电功率预测模型

2.1 预测模型构建

本文基于轻梯度提升机（LightGBM）［24］建立风电功率预测主模型。LightGBM 是一种经典的梯度上升决策树算法,与传统梯度提升算法不同,LightGBM 采用leaf-wise 生长策略,每次迭代都选择当前最大梯度的叶子进行分割。 因此,LightGBM 在相同复杂度下通常比传统梯度提升算法更准确。另一方面,LightGBM 使用基于直方图的方法来找到最佳的分割点。因此,LightGBM 具有非常优异的训练速度。

由于单特征的输入使LightGBM 模型无法充分捕捉目标变量的所有信息,本文通过构造时滞特征来模拟时间窗,进一步提升LightGBM 模型预测性能。对于预测标签y=[y1,y2,…,yt,…,yn],设定滞后周期τ,则可以构造时滞特征F=[F1,F2,…,Fτ],且Fτ=[yt-1,yt-2,…,yt-τ+1,yt-τ]。通过合并原始特征,输入特征更新为X=[T,F],即输入特征包括原始的时间特征和构造的时滞特征。

基于LightGBM 模型,训练主模型Regressor：

2.2 误差修正策略

现有算法未充分挖掘机器学习模型的潜力,构建的预测模型仅利用了模型的预测值,而未充分利用预测误差。针对上述问题,本文提出基于误差修正的改进风电功率预测模型,在训练风电功率预测主模型的基础上,增加误差预测模型,学习主模型的误差。本文构建的误差预测模型不依赖于误差分布的假设和先验知识,可以直接挖掘风电功率预测主模型的预测功率与真实功率之间的潜在关系。本文所述误差修正策略的算法流程如下。

2.2.1 构建误差预测模型

首先,基于Regressor 主模型计算训练集的功率预测值ŷtrain,即

考虑实际工程中,风电功率预测误差未知。因此,计算训练集预测值ŷtrain相比训练集标签ytrain的误差etrain,可表示为：

其次,构造误差预测模型Corrector 预测主模型Regressor 的误差,误差预测模型Corrector 的训练过程为：

式 中：concat(∙)表 示 将Xtrainnew和ŷtrain横 向 拼 接,作 为训 练 特 征 ；etrain作 为 预 测 标 签 。 在中拆分训练集和验证集,训练出误差预测模型Corrector。

2.2.2 风电功率预测修正

基于误差预测模块Corrector 进行预测的误差修正。首先,计算主模型Regressor 对测试集的功率预测值ŷtest：

最后,对ŷtest进行修正,得到修正值ŷcorr为：

本文所提模型结构如附录A 图A1 所示。

3 算例分析

3.1 数据集与评价指标

算例基于比利时Elia Group 的实际数据进行测试,该风电场数据集中包含2022 年1 月1 日—12 月31 日的风电发电功率数据,分辨率为15 min,本文预测时间尺度为超前15 min。选取测试集为12 月31 日。为避免偶然性,文中仿真数据均为3 次实验平均值。

为客观评价不同模型的预测结果,本文选取平均绝对百分比误差（mean absolute percentage error,MAPE）IMAPE、均方根误差（root mean square error,RMSE）IRMSE和拟合优度系数R2作为评价指标。MAPE 和RMSE 主要用来衡量预测值与实际值之间的偏差,其值越小,表明模型预测的准确度越高。R2衡量自变量与因变量的关系,R2∈[0,1]越接近1,表明模型的回归曲线拟合度越好。

式中：y为测试集标签ytest中的第i条数值；为中 的 第i条 数 值。

本文设定滞后周期τ=6 个,按照2.1 节所述构造6 条时滞特征,实现风电功率超前4 h 预测。LightGBM 模型的迭代次数设置为500,其余超参数均采用默认设置。基于原始特征和LightGBM 模型,训练基线模型LightGBM（下文简称LGB 模型）,性能指标分别为：IMAPE=7.677%,IRMSE=109.383,R2=0.970 6。

3.2 基于混沌噪声的特征衍生算例分析

3.2.1 混沌模型参数设置

由式（2）可知,状态变量x对新特征至关重要。由于Lorenz 方程是一个非线性、耦合且具有混沌特性的系统,对参数进行直接解析推断,进而确定适用于当前数据的超参数是困难的。因此,本文采用Optuna 算法［25］对Lorenz 系统的参数进行优化,自动计算出适应于本数据集的Lorenz 方程超参数。Optuna 是一个优秀的自动超参数优化软件框架,提供了多种优化算法,例如,贝叶斯优化、随机搜索和网格搜索等,可实现高效的超参数空间搜索。

设置σ的优化范围是［1,15］,ρ的优化范围为［1,40］,β的优化范围为［1,10］。采用Odeint 求解器求解式（1）,再通过式（2）构造衍生特征集合Xfakeh。设 置h=20。 基 于 此 时 的 特 征 集 合X=[T,F,Xfakeh]训练LGB 模型,并计算当前模型的RMSE。设置Optuna 算法的优化目标为最小化LGB 模型预测时的RMSE,迭代次数为100,仿真结果见图2。

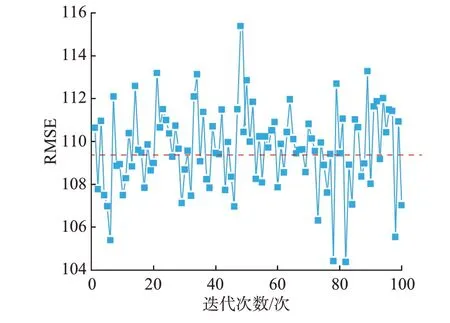
图2 基于不同参数混沌扰动衍生特征的模型性能Fig.2 Model performance based on chaotic disturbance derivation features of different parameters

图2 中红色虚线表示LGB 模型的RMSE 为109.383。由图可知,约有一半的数据在红线之下,其模型性能超越了LGB 模型的RMSE,验证了本文所提混沌扰动特征衍生策略的有效性和实验结果的非偶然性。RMSE 在第82 次迭代时最小,为104.36。

3.2.2 混沌扰动衍生特征数分析

基于优化出的最佳参数,通过式（2）构造衍生特征集合Xfakeh,训练基于不同h的X=[T,F,Xfakeh]所训练的LGB 模型,其性能变化见图3。图3（a）中水平虚线为LGB 模型的MAPE,图3（b）中水平虚线 为LGB 模 型 的RMSE,图3（c）中 水 平 虚 线 为LGB 模 型 的R2。

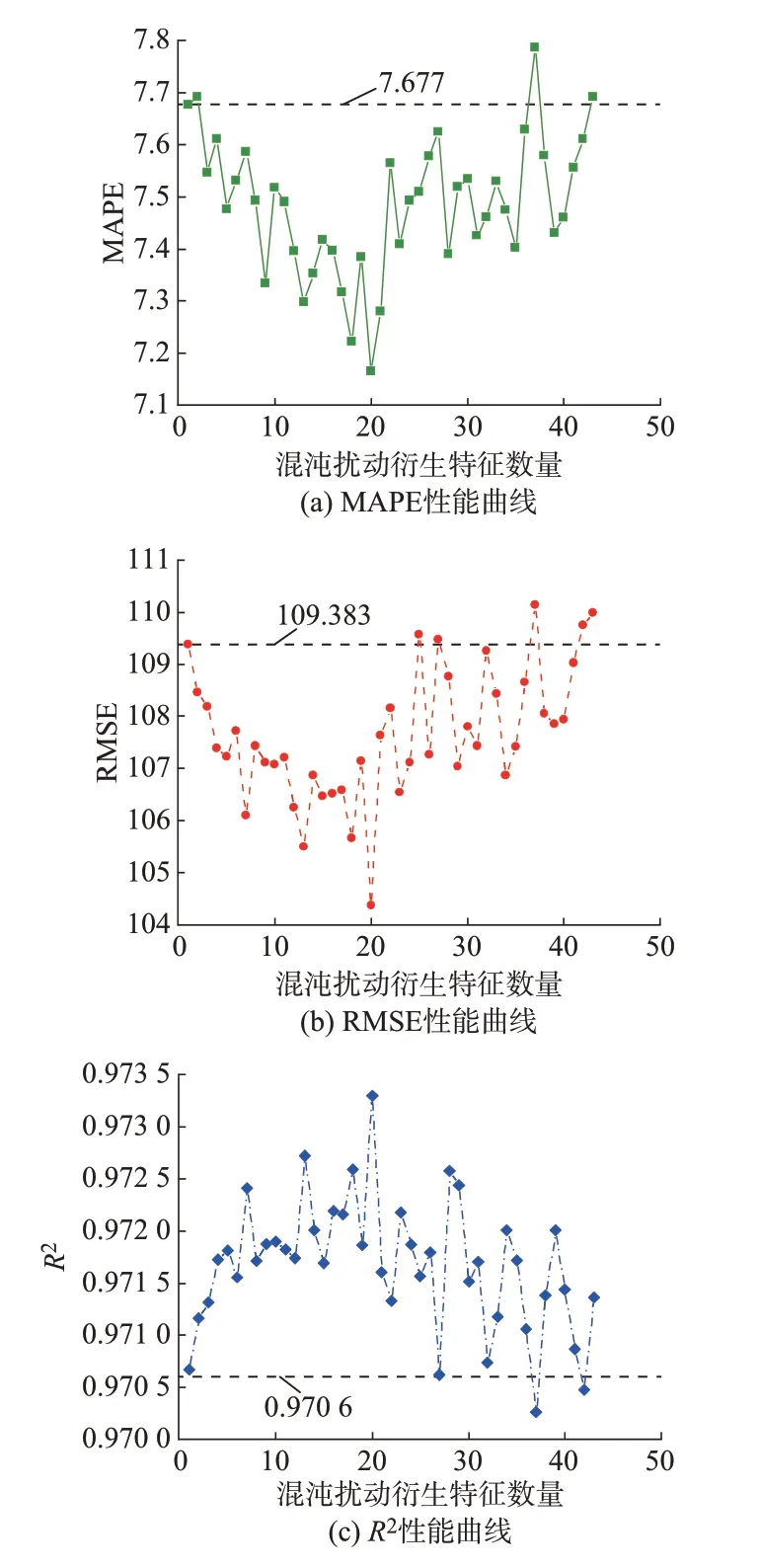
图3 基于不同数目衍生特征的模型性能Fig.3 Model performance based on different numbers of derivation features

由图3（a）可知,当衍生特征数量小于37 时,所训练出的大部分模型性能将超越基线模型性能。由图3（b）可知,当衍生特征数量小于26 时,所训练出的模型性能均超越了基线模型性能。由图3（c）可知,当衍生特征数量小于27 时,所训练出的模型性能均超越了基线模型性能。综上,模型性能随混沌扰动特征数量呈现振荡的先增后减趋势,当衍生特征数量为20 时,模型性能最好。

综上,当构造少量混沌扰动衍生特征时,将有助于提高模型性能,证明本文所提策略的有效性。但是,当构造的混沌扰动衍生特征数量较多时,模型性能将逐步变差,甚至将低于基线模型性能。这是由于引入混沌噪声的特征提升了数据的复杂度和随机度,过多地生成噪声特征会遮蔽数据原有的规律,进而削弱预测模型的性能。

3.2.3 基于混沌噪声的特征衍生算例结果

基于上述算例分析,本文选择构造20 条混沌衍生特征,训练所得模型CN20-LGB（chaos noise 20-LightGBM）,其性能达到了IMAPE=7.164%、IRMSE=104.36、R2=0.973 0。 相 较 于 基 线 模 型LGB,CN20-LGB 模型的MAPE 降低了6.68%,RMSE 降低了4.59%,R2提升了0.2%。

3.2.4 与其他类型噪声的算例对比

为了验证混沌噪声的效果与其他噪声的效果,本文将式（2）中的噪声更换为高斯噪声和白噪声,计算基于不同噪声扰动所得衍生特征的LGB 模型性能。

使用Optuna 算法优化高斯噪声的均值参数、标准差参数和方差参数,优化白噪声的功率谱密度参数、均值参数、方差参数和持续时间参数。设置Optuna 算法的优化目标为最小化LGB 模型预测时的RMSE,迭代次数为100。仿真结果见附录A 图A2。由仿真结果可知,在最佳参数时,基于高斯噪声衍生特征结果的模型的RMSE 为106.51,基于白噪声衍生特征结果的模型的RMSE 为105.26。

基于优化出的最佳参数,分别训练基于不同h的X=[T,F,Xfakeh]所训练的LGB 模型。选取最佳衍生数量的模型性能参数,将其与LGB 模型和CN20-LGB 模型进行性能对比,仿真结果如附录A表A1 所示。

由仿真结果可知,基于3 种不同噪声扰动衍生特征的模型性能均超过了LGB 模型的性能,其中,基于混沌噪声扰动衍生特征的模型性能最佳。由于风电功率输出具有一定的周期性或季节性,而混沌系统具有自相似性,即在不同的尺度上,都能观察到相似的结构。因此,相比其他噪声,混沌噪声更适合于具有周期性的风电功率预测。

3.3 基于IA 的特征衍生结果

设置IA 的维数M=26,抗体数量N=1 000,相似度阈值δ=0.9,亲和度权值a=0.8,浓度权值b=0.2,迭代次数为50 次,保留的衍生特征数量q=100。基于IA 的特征衍生策略,分别采用以下数据训练模型：

1）基于20 条混沌扰动特征和原始特征数据训练的模型CN20-IA-LGB。

2）基于原始特征数据训练的模型IA-LGB。

将上述两个模型与未使用基于IA 的特征衍生策略前的LGB 模型、CN20-LGB 模型进行性能对比,详细性能指标如表1 所示。

表1 特征工程性能指标对比Table 1 Comparison of performance indicators of engineering features

由表1 中的数据可知,采用基于IA 的特征衍生策略后,与基线模型LGB 相比,IA-LGB 模型的RMSE 降 低 了7.21%,MAPE 降 低 了7.28%,R2提升了0.41%。与CN20-LGB 模型相比,CN20-IALGB 模型的RMSE 降低了3.41%,MAPE 降低了2.97%,R2提升了0.31%。采用基于IA 的特征衍生策略后,模型均得到了性能提升,验证了本文所提基于IA 实现特征衍生的有效性与可行性。

3.4 基于误差修正策略的仿真结果

为验证2.2 节所提误差修正模型的可行性,将CN20-IA-LGB 模型作为主模型。根据式（10）计算该模型的预测误差etrain。将etrain与Xtrain进行相关性分析,得到Pearson 相关性系数和Spearman 相关性系数,如附录A 图A3 所示。由图A3 可知,风电功率预测误差与风电功率真实值的相关性极低,若采用传统预测模型来预测误差,则导致模型严重欠拟合,继而导致误差增大。解决该问题的思路在于模型集成和超参数自动调优,训练出优秀、互补的预测模型。

本文采用了HyperGBM 模型［26］对误差进行预测。HyperGBM 模型是一个结合了超参数优化和梯度提升决策树模型的集成学习框架。它的主要目标是自动化地寻找最优的模型架构和超参数,以在给定任务上达到最高的性能。HyperGBM 模型通过自动化搜索算法（如随机搜索、网格搜索或贝叶斯优化等）来选择超参数,从而减少了手动调参的需求。设置HyperGBM 模型的超参数均为默认参数,训练出的误差预测模型Corrector 的性能指标分别为：IRMSE=27.711,R2=0.013。

分别在LGB 模型和CN20-IA-LGB 模型的基础上,使用误差修正策略,训练修正后的模型,记为LGB-Correct 和CN20-IA-LGB-Correct 模 型,并 将其与修正前的模型性能对比,性能指标见表2。

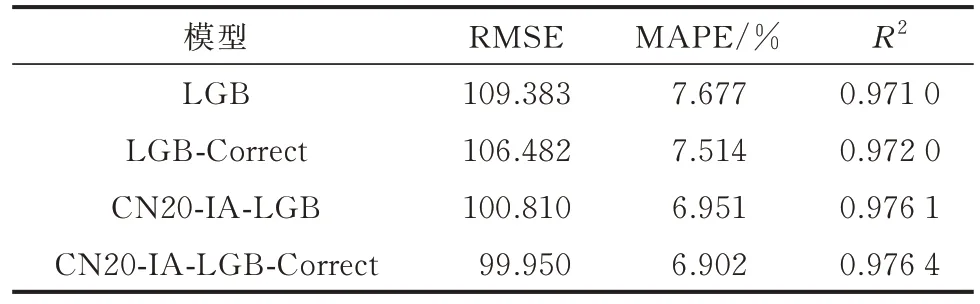
表2 误差修正前后模型性能对比Table 2 Model performance comparison before and after error correction

根据表2 中的仿真数据可知,误差修正后的模型比修正前的模型更加优秀。因此,即便误差预测模型Corrector 出现了欠拟合现象,增加了误差预测模型Corrector 后,主模型的预测性能依然有所提升。

预测器的误差与特征、预测值的相关性都极低,误差预测的效果较差。然而,如果误差预测模型是高性能的强学习器,它仍然有能力挖掘出预测误差与特征、预测值之间的微弱联系,并有效修正主模型的误差。

值得注意的是,修正策略后的LGB-Correct 模型的性能相比基线模型LGB 提升较大,CN20-IALGB-Correct 模型相比CN20-IA-LGB 模型也有性能提升,但是性能提升并不大。这是由于CN20-IALGB 模型预测精度很高,在数据种类较低、特征量较少的情况下,CN20-IA-LGB 模型接近极限,提升的空间较小。但基于本文所提出的误差修正模型,CN20-IA-LGB 模型依然有所提升。

此时,与原始的LGB 模型相比,CN20-IA-LGBCorrect 模型的RMSE 降低了8.62%,MAPE 降低了10.1%,R2提升了0.56%。

3.5 与当前主流算法对比

为进一步说明所提方案的有效性,本文将所提CN-IA-LGB-Correct 模型与当前主流机器学习模型进行对比,包括TabNet 模型、长短期记忆（LSTM）网络模型、LightGBM-CatBoost-XGBoost-Stacking（LGB-CTB-XGB-Stacking）模型。

TabNet 模型［27］是一种用于表格数据的深度学习网络结构,其性能已经超越了目前所有单体模型。LSTM 网络模型［20］是一种经典的循环神经网络变体,其特点是可以解决长期依赖问题。LGBCTB-XGB-Stacking 模型是将目前流行的梯度提升树 算 法LGB、CatBoost［28］和XGBoost［29］用Stacking算法集成后的模型。

TabNet 模 型、LSTM 网 络 模 型、LGB-CTBXGB-Stacking 模型的训练数据均使用原始的单特征风电功率数据,将训练后的模型性能与本文所提CN20-IA-LGB-Correct 模型性能进行对比,性能指标见表3,各模型的预测效果见附录A 图A4。

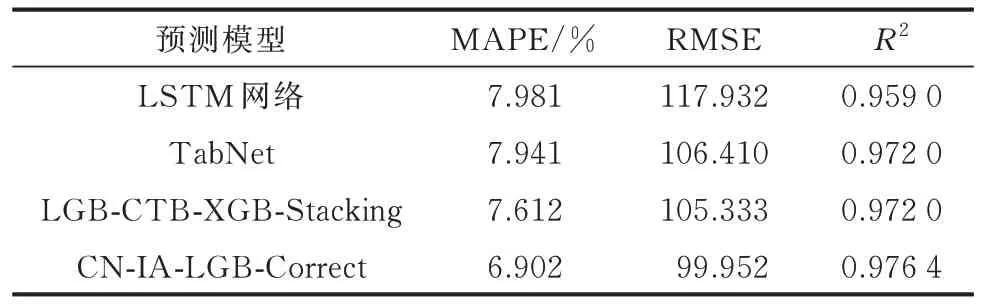
表3 不同模型性能指标Table 3 Performance indicators of different models

根据算例仿真可知,CN-IA-LGB-Correct 模型表现最佳,集成模型LGB-CTB-XGB-Stacking 和TabNet 模型表现次之,LSTM 网络模型表现最差。TabNet 模型和LGB-CTB-XGB-Stacking 模型的性能均超过了本文算例中的LGB 模型。而应用本文所述特征衍生策略和误差修正策略的LGB 模型不仅超越了自身的基线模型性能,也超越了TabNet 模型和LGB-CTB-XGB 模型的性能,验证了本文所提算法的有效性。

3.6 跨算法通用性验证

为了验证所提特征衍生算法在不同模型上的通用性和有效性,本文进一步将该算法应用于XGBoost 和TabNet 两种不同的模型。与LGB 模型不同,XGBoost 和TabNet 模型各自具有独特的模型结构和优化策略,这为本文所提算法提供了有力的测试场景。附录A 表A2 所示为XGBoost 模型使用本文所述特征衍生及误差修正算法后的仿真结果,附录A 表A3 所示为TabNet 模型使用本文所述特征衍生及误差修正算法后的仿真结果。由表A2 和表A3 可知,应用特征衍生算法及误差修正算法后,XGBoost 和TabNet 模型的性能均得到了提升,验证了本文所述算法的通用性和有效性。

4 结语

本文提出了基于混合特征双重衍生和误差修正的风电功率预测模型,以提高风电功率预测在数据种类不足及特征数量稀缺时的准确性。首先,提出混合特征双重衍生方法：1）通过在原始特征中施加混沌噪声,构造多条混沌扰动特征；2）通过设计基于IA 的特征衍生方法,显著增加了优质特征的数量。其次,构造了误差预测模型,通过预测风电功率预测误差,实现对风电功率预测主模型的误差修正,进一步提升了预测准确率。通过算例仿真与当前主流的LGB、TabNet、LSTM 网络、LGB-CTB-XGBStacking 模型进行对比,验证了本文所提模型的有效性和优越性。需要指出的是,本文通过所提出的特征衍生算法和误差修正模型,实现了在缺失天气预报数据时的风电功率超短期精确预测。但是,本文所提算法依然有一定局限性：当预测尺度较长时,即便应用本文所提特征衍生算法和误差修正模型后,预测精度仍然会急剧下降,无法实现基于单特征数据的中长期尺度准确预测。后续研究的重点是进一步改进特征工程算法,实现多时间尺度下的精确预测。

本文研究得到南瑞集团有限公司项目“信息-物理-社会元素的交互及协调技术(GFGFWD-210338)”资助,特此感谢!

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。