计及调频能力和经济效益的储能集群多状态区间优化策略

2024-03-29段潇涵

电力系统自动化 2024年5期

段潇涵，孙丹，赵琛，年珩

（浙江大学电气工程学院,浙江省杭州市 310027）

0 引言

全球范围内的能源危机和环境问题日益严峻,大力发展可再生能源已成为世界各国的共识［1-2］。随着可再生能源发电的快速布局,中国电力系统的电力电子化特性日益显著,以逆变器为主的并网接口存在阻尼和惯性支撑能力不足的问题,使得电力系统的频率安全面临着挑战［3-4］。

电化学储能拥有吞吐功率灵活、响应精度高等优势,在调频领域备受关注［5-6］。但受造价等因素的影响,国内目前的储能装机增速难以适应可再生能源发电的需求,现阶段的储能仍为一种稀缺的调频资源。因此,如何充分利用现有储能参与调频已有较多研究。文献［7］综合考虑荷电状态（state of charge,SOC）恢复的需求和电网频率的限制,解决了SOC 偏低或偏高时储能一次调频能力不足的问题；文献［8］根据电网的动态性能,提出一种基于输出调节理论的控制策略,提升了储能一次调频的响应速度；文献［9］通过人工设置一次调频死区确定储能的动作时机及调频深度,实现了风机和储能的联合频率控制；文献［10］通过负荷预测和模糊控制实时修正储能二次调频的功率分配因子,提升了储能在负荷持续扰动工况下的调频能力；文献［11］推导了储能的小信号模型和大信号模型,通过能量管理实现了一次调频、二次调频的协同。上述研究均针对单个电站,验证了储能在调频领域中的应用极具优势,但区域电网中多元化、多样化的分布式储能集群是未来的发展趋势［12］,进一步研究如何改善储能集群的调频效果非常必要。

储能集群的一次调频主要关注并网点的频率响应指标［13］,而二次调频本质上是一种无差调节,需要考虑储能集群内部的功率分配及控制中心的运算能力［14］。文献［15］针对储能集群二次调频提出一种使充放电效率最大化的功率分配策略,但并未关注经济效益。文献［16］提出以考核指标为导向分配功率,提高了储能集群的收益,但忽略了功率分配结果对二次调频成本的影响。文献［17-18］以最小化二次调频成本为目标,采用智能算法求解储能集群的功率分配问题,但调频效果受限于控制中心的运算速度。文献［19］通过构建二次调频耗量函数实现功率的最优分配,但耗量函数未能协调调频能力和经济效益间的关系。文献［20］提出一种双层优化策略,功率分配结果兼顾了储能集群的调频能力和经济效益,但忽略了不同单元间的SOC 差异［21］和控制中心的运算能力。

本文针对上述储能集群二次调频过程中所面临的问题,提出一种计及调频能力和经济效益的储能集群多状态区间优化策略；提出根据单元充放电效率及SOC 来划分状态区间的方法,以确保电量过低或过高的单元优先改善SOC；提出利用功率初次分配结果对单元输出功率进行约束的方法,以减少决策变量、降低控制中心的运算量；建立评估储能集群综合调频需求的优化模型,通过最优求解得到功率分配结果,以在保障储能集群调频能力的同时提升经济效益。仿真结果验证了本文所提优化策略的有效性。

1 含新能源及分布式储能集群的区域电网

假设含风、光等新能源发电系统的区域电网中包含I个储能电站,各电站在充放电效率、成本等方面存在差异。储能电站的结构参考2018 年投运的江苏五峰山储能电站［22］,每个电站内包含J个并联的电池预制舱,各电池预制舱可视作独立的储能单元,各单元通过变流器和升压变压器接入区域电网。

为满足区域电网的二次调频需求,储能集群需根据自动发电控制（automatic generation control,AGC）指令输出功率,如式（1）所示。

式中：PAGC（t）为t时刻的AGC 指令,在二次调频中该指令每4～6 s 更新一次［23］；Po,i,j（t）为t时刻第i个电站内第j个单元的输出功率。

风力和光伏发电均具有较强的随机性,导致AGC 有较大的不确定性。引入充放电标识α（t）描述储能集群的工作状态,当α（t）为-1 时储能集群充电,当α（t）为1 时储能集群放电,如式（2）所示。

2 多状态区间功率优化策略

2.1 多状态区间划分

多状态区间划分的目的在于根据SOC 来区分全部单元。对于SOC 距目标值较近的区间,功率分配的首要目标是降低调频成本；对于SOC 距目标值较远的区间,功率分配的首要目标是恢复SOC。

储能的总体效率为电池组效率与变流器效率的乘积。考虑到变流器的效率可以视作输出功率的一次函数,而电池组的效率与输出功率的函数较为复杂［15］。因此,为简化分析,本文将电池组的效率视作常数［19］,由储能类型所决定。t时刻第i个电站内第j个单元的充放电效率ηi,j（t）如式（3）所示。

式中：PN,i,j为第i个电站内第j个单元的额定功率；ai和bi为第i个电站内变流器的分段线性化系数；ci为第i个电站内电池组的效率。

划分状态区间的依据是SOC,由于SOC 过高或过低都不利于提升储能集群的调频能力,通常认为0.5 是理想的SOC 值。但以0.5 为SOC 目标值的优化存在偏差,原因是同样大小的充放电指令对SOC 的改变程度不同。定义t时刻第i个电站内第j个单元的电源功率Ps,i,j（t）反映充放电指令对SOC的改变程度,即

为平衡充放电调频能力,需根据效率确定储能单元的SOC 目标值,使SOC 等于目标值的储能单元在同样大小的充放电指令下能够维持相同的充放电时长。式（3）表明储能的效率是一个与输出功率相关的变量,这使得储能在一段时间内的平均效率难以预估。SOC 目标值的确定和多状态区间的划分需在调频开始前完成。因此,本文在确定SOC 目标值和划分多状态区间时,使用最大充放电效率ηi近似代替单元的效率,如式（5）所示。

考虑充放电效率差异的SOC 目标值由式（6）计算得到,详细推导过程见附录A。

式中：Sp,i为电站i的SOC 目标值；Smax,i和Smin,i分别为SOC 的最大值和最小值。为防止储能单元过度充放,SOC 大于Smax,i的单元被禁止充电,位于充电受限区间；SOC 小于Smin,i的单元被禁止放电,位于放电受限区间。

本文根据储能单元的调频需求划分5 个状态区间。电量较低或较高的单元分别被划入低电量区间和高电量区间；电量适中的单元被划入均衡区间。由于均衡区间内单元的调频需求与高、低电量区间差异较大,在高、低电量区间和均衡区间之间分别增设高电量过渡区间和低电量过渡区间,以平衡两种调频需求。5 个区间对应6 个临界值,所受约束如式（7）所示。

式中：Smin,i和Slow,i为第i个电站内低电量区间的临界值；Slow,i和Sp,c,i为第i个电站内低电量过渡区间的临界值；Sp,c,i和Sp,d,i为第i个电站内均衡区间的临界值；Sp,d,i和Shigh,i为第i个电站内高电量过渡区间的临界值；Shigh,i和Smax,i为第i个电站内高电量区间的临界值。计算临界值的辅助矩阵A见附录A式（A5）。

定义状态区间值以反映全部单元所处的状态区间,如式（8）所示。

式中：Sf,i,j（t）的值代表t时刻第i个电站内第j个单元所处的状态区间,从1 到5 依次代表低电量区间、低电量过渡区间、均衡区间、高电量过渡区间和高电量区间；Si,j（t）为t时刻第i个电站内第j个单元的SOC 值。

需要说明的是,本文仅在确定SOC 目标值和划分多状态区间的过程中使用最大充放电效率近似代替储能单元的效率,在建立优化模型时,本文仍使用式（3）计算储能效率,储能的充放电损耗作为调频成本的一部分影响功率分配,经优化求解得到的功率分配结果倾向于使各单元以尽可能高的效率输出功率。因此,上述近似处理有一定的合理性。

2.2 功率的初次分配

本文所提策略以状态区间为单位完成功率的初次分配。根据α（t）确定当前时刻不同区间的出力优先级,当α（t）为负时,SOC 越小的区间出力优先级越高,反之,SOC 越大的区间出力优先级越高。

计算各区间的极限功率以评估储能集群的调频能力。以充电工况为例,极限功率的计算如式（9）所示,详细推导过程见附录B。

式中：P1（t）、P2（t）、P3（t）、P4（t）、P5（t）分别为低电量区间、低电量过渡区间、均衡区间、高电量过渡区间、高电量区间的极限功率；B为计算极限功率的辅助矩阵。

根据极限功率和AGC 可以确定当前时刻的优化区间。充电工况下优化区间的标识Sa（t）由式（10）确定。

式中：Sa（t）对应的数值与Sf,i,j（t）所对应的数值含义相同,Sa（t）为0 意味着储能集群无法满足电网的要求。

针对当前时刻非优化区间内的储能单元,可以直接确定出力。与优化区间进行优先级比较,优先级高的区间内的单元以额定功率出力,优先级低的区间内的单元出力为0,即增加如下约束：

2.3 优化区间的功率分配策略

2.3.1 目标函数

首先,建立反映调频成本的目标函数。本文采用就地平衡的方式调频,忽略网损和变压器损耗后t时刻储能电站i的调频成本Cb,i（t）由投资建设成本Cinv,i（t）、能量损失成本Closs,i（t）［20］和寿命衰减成本Clife,i（t）［24］组成。其中,投资建设成本为固定成本,不影响功率分配,而能量损失成本和寿命衰减成本可以视作各电站输出功率的函数,如式（12）所示。

式中：Sp,m为能量市场的最大单位利润；ΔT为控制周期的步长；Ps,i（t）、Po,i（t）分别为t时刻第i个电站的电源功率和输出功率；cm,i、PN,i分别为第i个电站的单位功率成本和额定功率；N0,i为第i个电站的等效循环次数；kp为常数,通常在0.8～2.1 之间［25］,本文取1；EN,i为第i个电站的额定容量。

储能集群的调频成本等于所有电站的调频成本之和,可以视作体现经济效益的基本目标函数Z1,如式（13）所示。

为提升储能集群的充放电调频能力,需要建立反映储能集群整体SOC 的目标函数。引入SOC 恢复系数αi,j（t）来反映各单元恢复SOC 的迫切程度,如式（14）所示。

反映储能集群整体SOC 的基本目标函数Z2如式（15）所示。

需要说明的是,在短期调频中,对Z2的优化可能使调频成本上升,但在长期调频中,对Z2的优化能使储能集群更好地满足区域电网的考核要求,从而间接改善储能集群的经济效益。

由于Z1和Z2数量级不同,在合成前需进行归一化,而非优化区间内单元的出力已由式（11）确定。因此,目标函数的决策变量仅为优化区间内K个单元的输出功率。为简化计算,根据式（16）对优化区间内的K个单元进行等比例功率分配,得到估算的功率分配结果。

式中：Pesm,k（t）为t时刻优化区间内第k个单元的估算功率；P′AGC(t)为t时刻控制中心分配给优化区间的总功率；PN,k为第k个单元的额定功率。

将式（16）的结果分别代入式（13）和式（15）,得到两个基本目标函数的估算值,分别记为Zesm,1和Zesm,2。最优求解对调频成本的期望是越小越好,对储能单元整体SOC 的期望是与目标值之差越小越好。因此,两个目标方向一致,可以在归一化后直接合成为Z,如式（17）所示。

式中：αz,c和αz,s分别为目标函数Z1和Z2的比例系数。

以各单元的输出功率为决策变量,将式（12）—式（15）代入式（17）,得到展开的合成目标函数如式（18）所示。

式中：EN,i,j为第i个电站内第j个单元的额定容量。

由式（18）可知,储能集群的功率分配被描述为一个凸二次规划问题。对商业求解器而言,这是一个相对简单的优化问题,存在唯一的功率分配结果使目标函数的值最小［26］。

为区分不同区间的调频需求,需根据式（19）约束比例系数的相对大小。

需要说明的是,式（19）的约束是松弛的,在实际应用中可以适度调整比例系数的相对大小,从而改变对不同调频需求的侧重程度。此外,考虑到前文采用等比例法估算得到的基本目标函数值存在误差,且总成本的大小对功率分配结果较为敏感,本文在过渡区间的优化中增设了成本-SOC 排序约束。

2.3.2 约束条件

以充电工况下的低电量过渡区间为例,对区间内的单元进行成本-SOC 排序。假设区间内包含N个储能单元,根据式（20）计算单元n的单位调频成本Ce,n。

将N个单元的成本与各自的SOC 分别归一化后相乘,再由低到高排序,在过渡区间中增加式（21）对序号分别为x1、x2的两个单元的输出功率进行约束。过渡区间和其余区间的优化结果对比见附录C。

储能电站的输出功率受其内部单元输出功率的限制,增加功率约束如式（22）所示。

由于AGC 可能超过储能集群的极限功率,需分别设计功率约束：储能集群能够跟随AGC 时,约束如式（23）所示,反之,约束如式（24）所示。

储能单元的SOC 会不断变化,为防止过充过放,增加SOC 约束如式（25）所示。

式中：ΔSi,j（t）为第i个电站内第j个单元的SOC 在一个控制周期内的变化量。

以式（18）为优化目标,以式（21）—式（25）为约束条件,得到评估储能集群综合调频需求的优化模型。在MATLAB 中调用商业求解器对本文所建立的优化模型进行求解,根据优化结果控制各单元输出功率。本文所提多状态区间功率优化策略的流程如图1 所示。

2.4 控制效果评价指标

结合本文所提策略的特点,定义以下4 个控制效果评价指标。

1）能量偏差Eb：

Eb用于评价T个控制周期内调频出力与AGC指令的偏差,将功率缺额换算成能量缺额后进行累加,单位为kW·h。

2）SOC 偏差Sb,i（t）：

Sb,i(t)用于评价第i个电站内部整体的SOC,取值范围为0 到1,Sb,i（t）越小表明该电站的充放电调频能力越均衡。

3）单位调频价格CFM：

式中：Cmax为成本最高的电站的单位调频价格。

CFM用于评价储能集群参与调频的平均电价,单位为元/（kW·h）。由1.2 倍的最高单位调频价格与能量偏差相乘得到缺额成本,缺额成本代表了区域电网在储能集群无法满足调频考核指标时对其所下发的考核惩罚。

4）优化时长ta。ta用于评价控制中心的平均计算时长,单位为s,ta越小表明优化速度越快。

3 仿真案例分析

3.1 储能电站SOC 目标值验证

为验证式（6）计算得到的SOC 目标值能够有效平衡储能电站的充放电调频能力,在MATLAB 中对两个SOC 初值不同的电站进行仿真分析。两个电站参数相同且SOC 偏差一致,电站1 以0.5 为目标值,电站2 以式（6）计算出的Sp,i为目标值,在相同的AGC 下按等比例分配策略分别仿真,得到图2 所示的结果。

图2 不同SOC 目标值下的二次调频能力对比Fig.2 Comparison of secondary frequency regulation capability under different target values of SOC

由图2 可知,以同样大小的充放电指令控制电站1 参与调频,其充电调频能力所维持的时间比放电调频能力所维持的时间长5.8 min,在放电调频进行到大约12 min 时,电站1 内全部储能单元的SOC均低于Smin,电站失去放电调频能力,而充电调频能力则可以维持到18 min 附近；利用式（6）对SOC 目标值进行修正后,电站2 的放电调频能力得到了提升,放电调频所维持的时间仅比充电调频短0.4 min。因此,可以认为在利用式（6）对SOC 目标值进行修正后,相同指令下电站的充电调频能力和放电调频能力基本一致。不同目标值下的SOC 均值曲线见附录D。

3.2 储能集群调频能力及经济效益验证

3.2.1 系统设计

为验证本文所提多状态区间优化策略的优越性,在MATLAB 中设计包含新能源及储能集群的区域电网。假设新能源的装机容量为425 MW,储能的装机容量占新能源的20%,包含4 座类型不同的电站,每个电站由并联的10 个可单独控制的单元构成。各电站基本参数见表1,各单元SOC 初始值见表2,单元的充放电受限值分别为0.9 和0.1,仿真时长为100 min。

表1 储能电站参数Table 1 Parameters of energy storage power stations

表2 储能单元SOC 初始值Table 2 Initial SOC values of energy storage units

3.2.2 调频能力对比分析

采用双层优化策略［20］与本文所提策略进行对比。双层优化策略的原理如下：在功率优化层,根据储能电站的调频成本和剩余调频能力确定优化目标；在SOC 优化层,根据储能单元的SOC 确定优化目标。在上文所述的系统中,分别采用双层优化策略和本文所提策略控制储能集群,得到的响应曲线如图3 所示。由图可知,在52 min 之前,AGC 要求储能集群随机充放电且数值较小,此时的储能集群可以通过调频改善内部单元的SOC,同时兼顾经济效益；在52 min 之后,AGC 始终为正且数值接近额定功率,这一阶段储能集群对AGC 的跟随程度可以反映其持续放电能力。

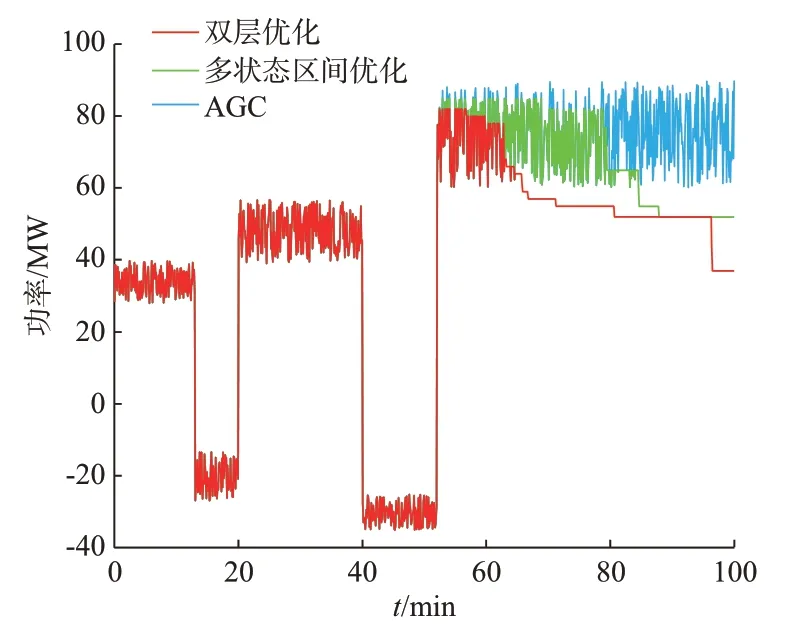
图3 不同策略下储能集群的响应曲线Fig.3 Response curves of energy storage clusters under different strategies

由图3 可以看出,双层优化策略下的储能集群在62 min 左右出现了明显的功率缺额,而多状态区间优化策略下的储能集群直到79 min 左右才出现功率缺额,下文具体分析出力存在偏差的原因。

各储能电站的出力对比如图4 所示。

图4 不同策略下各储能电站的出力对比Fig.4 Comparison of output of energy storage power stations under different strategies

由图4 可以看出,在0～13 min 内,双层优化策略下的电站2 由于调频成本较低得到了较多功率,电站1 则由于成本过高无法在这一阶段分配到足够的功率。而多状态区间优化策略下的储能集群考虑到电站1 内有5 个位于高电量区间的单元,故分配10 MW 功率给电站1；电站2 的SOC 偏差较小,基本不参与放电；电站3 内部有7 个单元SOC 较高,故功率在21 MW 附近波动；电站4 内部有3 个单元SOC较高,故功率在6 MW 附近波动。在13～20 min 内,双层优化策略将大部分充电功率分配给了电站4,多状态区间优化策略则兼顾了电站1 和电站4 的充电需求。在20～40 min 内,多状态区间优化策略下的功率分配开始更多地考虑经济效益,成本最低的电站2 承担了较多功率。同时,电站1 和电站3 由于自身需求仍能够获得稳定的功率。在40～52 min内,多状态区间优化策略下的电站4 承担了最多的功率,电站1 内部的单元利用前期的调频恢复了自身的SOC,故电站1 的功率逐渐减小。在52 min 之后,电网的AGC 指令接近储能的额定功率,这一时段内功率分配的自由度较小,功率缺额的增加意味着有越来越多的单元被禁止参与调频。

不同策略下各电站的SOC 偏差如图5 所示。在52 min 之前,双层优化策略下电站1 的SOC 偏差几乎不变,电站2 的SOC 偏差在明显升高之后略有下降,电站3 的SOC 偏差不断降低,电站4 的SOC偏差反复升降。多状态区间优化策略下,电站1、电站3、电站4 均充分利用了这一时段内的调频过程降低了SOC 偏差,大大提升了储能集群的调频能力,而电站2 内部单元初始时刻的SOC 非常接近目标值,后续的调频虽增大了其SOC 偏移,但其偏移量仍相对较小。在随机充放电结束的时刻,多状态区间优化策略下各电站的调频能力明显更强。因此,在持续放电阶段能够更好地跟随AGC 指令。

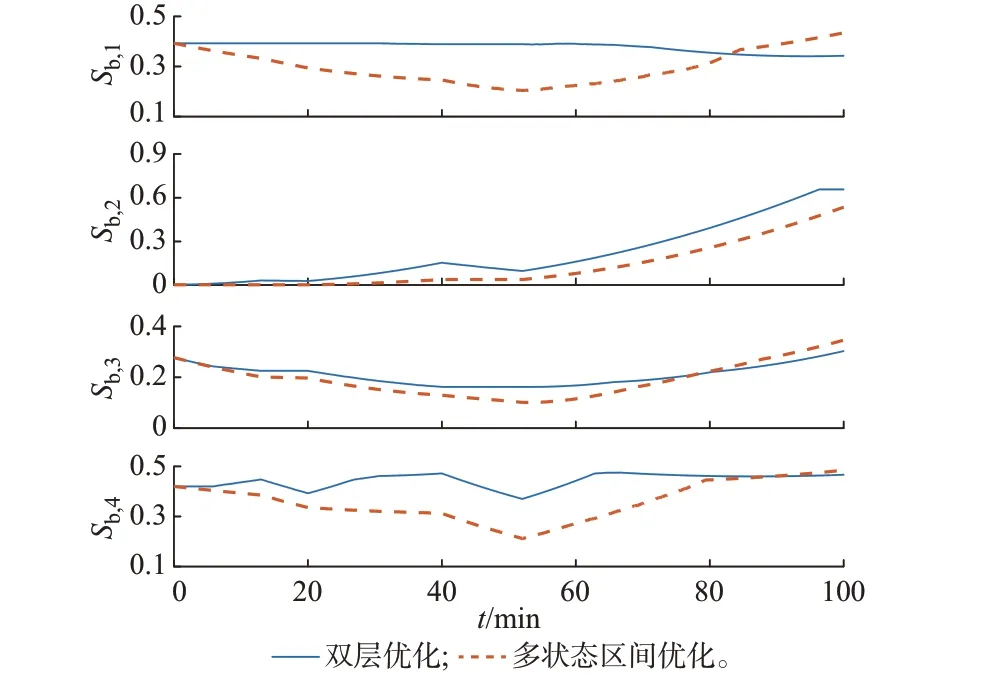
图5 不同策略下的SOC 偏差Fig.5 SOC deviation under different strategies

由于二次调频的时间尺度相对较短,不足以使储能电站的容量发生明显变化［27］,本文在分析调频能力时假设各电站的容量未发生衰减。在实际的工程应用中,频繁的调频出力会加速储能的容量衰减。因此,应用于调频服务的电站的实际寿命很可能低于预期值,在其服役后期,电站的容量必然发生了一定程度的衰减。考虑容量衰减的调频能力对比分析见附录E。

3.2.3 经济效益及仿真时长对比分析

本文所提优化策略下各状态区间数量的变化如表3 所示。初始时刻,储能集群内有23 个单元位于高电量区间和低电量区间。因此,仿真开始阶段储能集群调频的主要目标是改善SOC,随着调频的进行,越来越多的单元脱离高电量区间和低电量区间。在40 min 时,储能集群内有28 个单元位于过渡区间和均衡区间,此时的功率分配将主要依据调频成本的高低来进行,这一阶段的功率分配能够有效提升储能集群的经济效益。

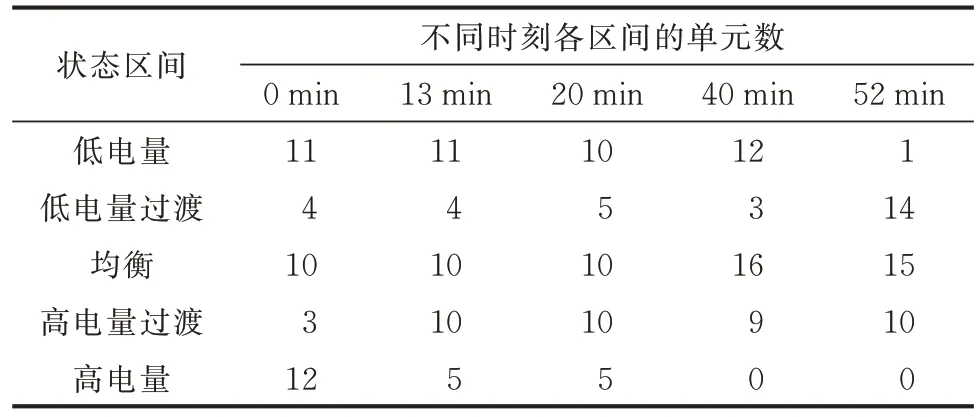
表3 各状态区间的数量Table 3 Number of each state interval

不同策略下的经济效益如表4 所示。根据上文分析可知,本文所提策略下的电站1、电站3 和电站4均利用前期的调频过程降低了SOC 偏差,增强了充放电调频能力。与双层优化策略相比,本文所提优化策略下的电站1 和电站3 输出了更多的功率,直接计算得到的调频成本也相对更高。但由于双层优化策略在前期调频过程中没有充分考虑各储能单元恢复SOC 的需求,在后期调频过程中产生了较大的能量偏差,这就导致双层优化策略下反映区域电网奖惩机制的缺额成本明显升高。而多状态区间优化策略减小了储能集群的能量偏差,降低了缺额成本,从而使得储能集群的总成本和单位调频价格下降了约20%。可见,本文所提策略能够有效提升储能集群的调频能力和经济效益。

表4 不同优化策略下的经济效益Table 4 Economic benefits under different optimization strategies

此外,为验证本文所提策略在运算速度方面的优势,在同一台计算机上先后对两种优化策略进行仿真,并调用MATLAB R2022b 中的YALMIP 工具箱完成求解。计算机的CPU 为AMD R7-5800H,8 核心16 线程,内存大小为16 GB,频率为3 200 MHz。记录仿真总时长后,得到双层优化策略平均每次功率分配需0.746 s,而本文所提策略平均每次功率分配只需0.083 s。可见,本文所提策略能够有效提升优化速度,从而在更短的时间内为储能单元下发控制指令,发挥储能灵活吞吐功率的优势。