纤维增强复合材料层压板的疲劳寿命预测方法

2024-03-28徐蓉霞高建雄朱鹏年吴志峯

上海交通大学学报 2024年3期

徐蓉霞, 高建雄, 朱鹏年, 吴志峯

(新疆大学机械工程学院,乌鲁木齐 830017)

纤维增强复合材料(Fiber Reinforced Polymer, FRP)具有比强度高、比刚度大、寿命长、结构可设计[1-3]等诸多优点,因此其在近几十年来应用较为广泛[4]. 在工程实际应用中,导致其结构破坏的重要原因包括疲劳损伤造成的断裂,但FRP有多种形式的损伤,且疲劳破坏机理十分复杂[5-6]. 在疲劳过程中,各种形式的损伤互相影响,不断累积,FRP的机械性能也随之发生退化[7]. FRP的疲劳寿命模型一般是根据应力-寿命曲线(S-N曲线)或Goodman疲劳寿命曲线来预测特定载荷下的疲劳寿命. 这种方法不考虑疲劳损伤的微观机理、材料的性能退化、损伤之间的耦合和损伤的累积,而且往往需要大量的实验数据来建立疲劳寿命曲线. 或者通过渐进疲劳损伤分析模型来预测其疲劳寿命,该方法涵盖疲劳加载过程中应力分析、疲劳失效准则和材料性能退化模型3部分. 因此,FRP层压板的疲劳寿命,可以基于经典层压板理论分析单层板的应力来预测,但该计算过程繁琐,且认为同一单层板的受力均匀,因此预测误差较大. 基于以上问题,本文提出了单向板的载荷水平-疲劳寿命曲线(q-N曲线),与层压板的有限元分析紧密结合来预测FRP层压板的疲劳寿命方法.

目前用于表征复合材料疲劳损伤扩展的参量有疲劳模量、剩余强度、应变等物理量,基于这些物理量,可以构造出多种疲劳损伤和疲劳寿命模型[8-9]. 本文用疲劳模量来描述碳纤维增强复合材料的损伤演化规律,从而建立疲劳寿命的函数表达式. 以单向板在单轴循环应力加载下载荷比与疲劳寿命的试验数据为基础,利用灰色系统等间距GM(1, 1)模型[10],构造单向板的疲劳寿命和损伤函数模型.

复合材料的疲劳过程从本质上讲是损伤不断累积,材料性质不断退化,应力重新分布的动态过程[11-12]. 本文将FRP层压板的疲劳失效过程简化为:在应力加载下,单层板的危险单元失效,导致该单层的材料性质发生改变,从而对该层材料进行刚度退化,随之应力分布改变的循环过程. 利用Abaqus对层压板建模分析,获取每单层的应力分布,进而提取危险点的应力,通过Hashin损伤失效准则[13],判断该层的失效模式,然后对失效单层进行刚度退化,循环该过程,确定单层的失效强度以及层压板的拉伸强度. 通过该有限元分析过程中所得的应力分布,与灰色系统建立的单向板的疲劳寿命计算公式结合,以此来预测FRP层压板的疲劳寿命. 通过与实验数据以及其他文献方法的预测结果对比,来验证该方法的有效性.

1 基于灰色系统GM(1, 1)模型建立单向板的q-N函数

灰色系统理论是一种研究“小样本”“贫信息”不确定性问题的方法,主要提取“部分”已知信息,实现对系统演化规律的正确描述[14]. 灰色预测建模方法种类繁多,其中等间距GM(1, 1)模型具有样本需求小、建模过程简单等优点. 当建立单向板的疲劳寿命预测模型时,在实验数据较少的情况下,若用最小二乘法拟合函数曲线,将导致误差较大. 因此,借助灰色系统建立单向板的疲劳寿命函数,首先引入疲劳模量衰减的双参数模型.

1.1 疲劳模量的概念

Hwang等[15]首先引入疲劳模量的概念,提出通过疲劳模量来预测疲劳寿命. 文献[16]中以碳纤维为研究对象,给出了循环应力最大值与应力循环次数n有关的疲劳模量的定义:

(1)

式中:σmax为外加循环应力的最大值;En为第n个循环时的疲劳模量;载荷比q表征应力水平,q=σmax/σu,σu为极限强度;εn为第n个循环后的累积应变,包含了第n次循环时的弹性应变.

En的初值、终值条件为

(2)

式中:E0为材料的静态弹性模量,在工程上,假定n=0时的疲劳模量等于E0;EN为经过N个循环后,材料发生疲劳破坏时的疲劳模量,N即为疲劳寿命.因此,E0是常数,EN取决于外载荷. Hwang等[17]提出了疲劳模量衰减三参数模型以及可以简化的双参数模型. 其中,如下式所示的双参数模型的疲劳寿命预测值与实验数据吻合较好,而且简单,因此本文选用此模型预测疲劳寿命:

(3)

式中:A、B均为材料常数.

1.2 FRP单向板的疲劳寿命分析

以单向板受纵向拉-拉循环载荷为例,来说明单轴循环应力下单向板疲劳寿命的计算方法. 定义如下物理量[18]:

(4)

式中:Xt为单向板的纵向拉伸强度;εut为纵向静态极限应变;E11为纵向静态弹性模量;εN表示疲劳破坏时的极限应变.将式(3)从第n1个循环到第n2个循环进行积分:

(5)

令nn=n,n1=1,式(5)可以简化为

(6)

(7)

假设单向板在承受N次循环载荷后发生疲劳破坏,那么EN便可作为疲劳模量的临界值.令k1=εN/εut,则N可以表示为

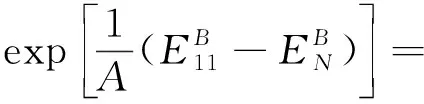
(8)

(9)

式中:a1、k1均为材料参数.当B=1时,式(9)简化为N=exp[a1(k1-q)].

1.3 损伤函数的构成

假设复合材料无初始损伤,疲劳损伤函数的定义Dn=(εn-ε0)/(εN-ε0)应满足下列初值、终值条件:

(10)

以单向板受纵向单轴循环应力作用为例,以应变和疲劳模量为中间量,建立损伤函数,其过程如下:

(11)

同样的方法,可以建立单向板在其他两个主轴方向上(横向和面内剪切)形如式(11)所示的疲劳损伤函数. 因此三参数和双参数疲劳损伤累积公式分别如下所示:

(12)

(13)

根据式(12)和式(13)所示的损伤累积公式,计算单向板在3个主轴方向上循环应力加载造成的损伤,分别表示为:D1、D2、D12.考虑多向应力的综合作用效果,定义复合型损伤:

(14)

式中:D11表示多轴循环应力加载下纤维的损伤程度;D22则反映基体的损伤程度. 只要其中任何一个首先达到1,单向板就发生了疲劳失效. 但疲劳极限本身存在模糊性,因此当复合型损伤很接近1时单向板也有可能发生了疲劳失效.

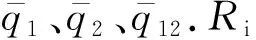
(15)

式中:Yt为横向拉伸强度;Sin为面内剪切强度;σ1,max、σ2,max表示纵向和横向两个方向上的最大主应力;τ12,max为剪切方向最大应力;νij表示应力作用在i方向时,在j方向引起的横向变形的泊松比,i,j=1, 2.将等效载荷比代入建立的q-N函数表达式中,计算对应的疲劳寿命.

1.4 灰色系统等间距GM(1, 1)建模

灰色系统模型通过序列的累加生成,揭示系统的发展趋势,累加生成处理后的序列呈现单调递增的规律. 设X(0)为原始序列,X(1)为一次累加生成序列,Z(1)为均值序列,表达式为X(0)=[x(0)(1)x(0)(2) …x(0)(n)],X(1)=[x(1)(1)x(1)(2) …x(1)(n)],Z(1)=[z(1)(1)z(1)(2) …z(1)(n)].

其中,累加序列当序列数k=1时,x(1)(1)=x(0)(0),当k为其他值时,如下式所示:

x(1)(k)=(x(0)(k)+x(1)(k-1))

(16)

k=2,3,…,n

均值序列为

z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),

k=2,3,…,n

(17)

则x(1)上的灰微分方程为x(0)(k)+az(1)(k)=b,其白化方程为dx(1)/dt+ax(1)=b.其中,参数a和b根据下式计算:

(18)

(19)

参数C、D、E、F可以根据原始序列、一次累加序列以及均值序列得到:

(20)

(21)

(22)

(23)

白化方程式的解为x(1)(t)=(x(1)(1)-b/a)exp(-at)+b/a,其中t表示时间,则灰色系统GM(1, 1)模型的时间响应序列为x(1)(k+1)=(x(0)(1)-b/a)exp(-ak)+b/a,其中k=1,2,…,n.因此,该模型的预测结果计算式如下:

x(0)(k+1)=x(1)(k+1)-x(1)(k)=

(24)

k=1,2,…,n

设单层板在单轴循环应力作用下,不同载荷比下的疲劳寿命视为一个灰色系统中,疲劳寿命构成一个原始序列,根据灰色等间距GM(1, 1)建模,扩展实验数据,然后拟合q-N函数曲线.

1.5 基于灰色系统建立FRP单层板在单轴循环应力作用下的q-N曲线和损伤函数

对于T300/QY8911复合材料单向板[0]16, 文献[19]中给出了应力比R=0.1时的纵向拉-拉疲劳试验数据,如表1所示.

表1 [0]16单向板在纵向应力作用下疲劳试验数据

首先,用最小二乘法拟合双参数和三参数q-N曲线的函数表达式如下所示:

q=-0.035lnN+1.189

(25)

q=(1.778×10-5lnN+2.132)-6.597

(26)

建立灰色等间距模型时,需要等间距载荷比下的疲劳寿命,根据插值法,计算q=0.75时的N=2.71×105. 因此灰色等间距GM(1, 1)模型原始序列可以设为X(0)=[2.50×1032.40×1041.43×1052.71×1054.57×105],根据式(16)～(23),计算一次累加序列和均值序列,C=1.086 5×106,D=8.95×105,E=4.027 5×1011,F=5.504×1011,a=-0.625 4,b=53 882.根据式(24)计算当q=0.65,0.6,0.55,0.5时,N=9.40×105,1.76×106,3.28×106,6.14×106.在灰色系统建模时,发现q=0.85时曲线突变,因此将该曲线分段,拟合的双参数和三参数q-N函数,分别如下所示:

(27)

(28)

将4种方法进行误差对比分析,结果如表2所示.

表2 拟合[0]16单向板q-N函数不同方法的精度对比Tab.2 Precision comparison of different methods for fitting q-N function of [0]16 uni-directional plates

由表2可知,最小二乘法拟合三参数q-N函数的方法误差太大, 因此不再做函数曲线图.其他3种方法的q-lgN函数曲线如图1所示.

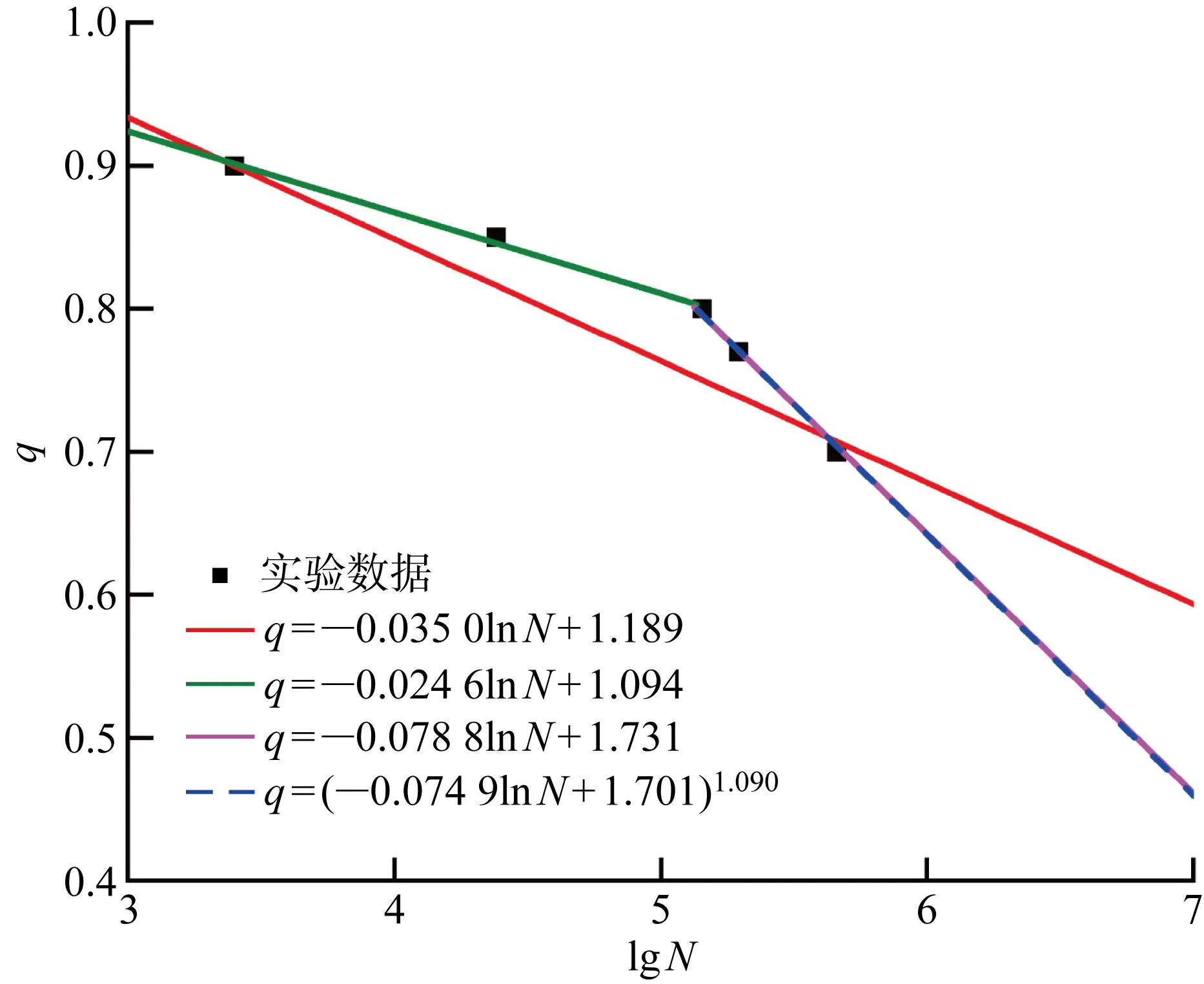
图1 3种建模方式拟合[0]16单向板的q-lg N曲线Fig.1 Fitting of q-lg N curves of [0]16 uni-directional plates of three modeling methods

通过表2和图1可以发现,通过灰色系统建立的q-N函数,精度明显得到了提高. 本文在计算纵向损伤量时,选用拟合曲线与实验数据相对误差最小的灰色系统拟合的三参数q-N函数. 因此损伤函数为

(29)

横向拉-拉建模数据根据[90]20单向板拉-拉疲劳实验获得[19],如表3所示.

表3 [90]20单向板在横向应力作用下的疲劳实验数据(R=0.1)

首先,用最小二乘法拟合q-N函数. 拟合双参数q-N曲线的函数表达式如下所示:

q=-0.036 4lnN+1.128

(30)

拟合三参数q-N函数的发展趋势不符合复合材料q-N函数发展趋势,因此暂不考虑该方法. 根据插值法,计算出q=0.95,0.85,0.75时,N=550.5, 2.245×103, 8.124×104. 灰色等间距模型原始序列设为X(0)=[550.5 1.01×1032.245×1033.48×1038.124×1041.59×105]. 根据式(16)～(23)计算一次累加序列和均值序列,C=225 215,D=246 975,E=3.063 4×1010,F=3.056 7×1010,a=-0.955 3.根据式(24),计算当q=0.65,0.6,0.55时,N=1.369 1×106,3.559×106,9.251 4×106.将这9组数据,用最小二乘法拟合双参数和三参数q-N函数,结果如下所示:

q=-0.034 1lnN+1.111

(31)

q=(0.27lnN-0.519)-0.391

(32)

将基于横向拉-拉疲劳试验数据的3种拟合方法的误差进行对比分析,结果如表4所示.

表4 拟合[90]20单向板q-N函数不同方法的精度对比Tab.4 Precision comparison of different methods for fitting q-N function of [90]20 uni-directional plates

3种方法拟合的q-lgN函数曲线,如图2所示.

灰色系统拟合的q-N三参数方法的误差最小,根据损伤函数,计算3个参数时发现,参数k不是实数,不能计算本文运用的损伤函数. 因此,选用灰色系统拟合的双参数q-N函数. 所以损伤函数为

(33)

面内剪切疲劳实验数据,根据[0/90]4s剪-剪疲劳实验获得[19],如表5所示.

根据这5组数据,用最小二乘法拟合双参数和三参数q-N函数,结果如下所示:

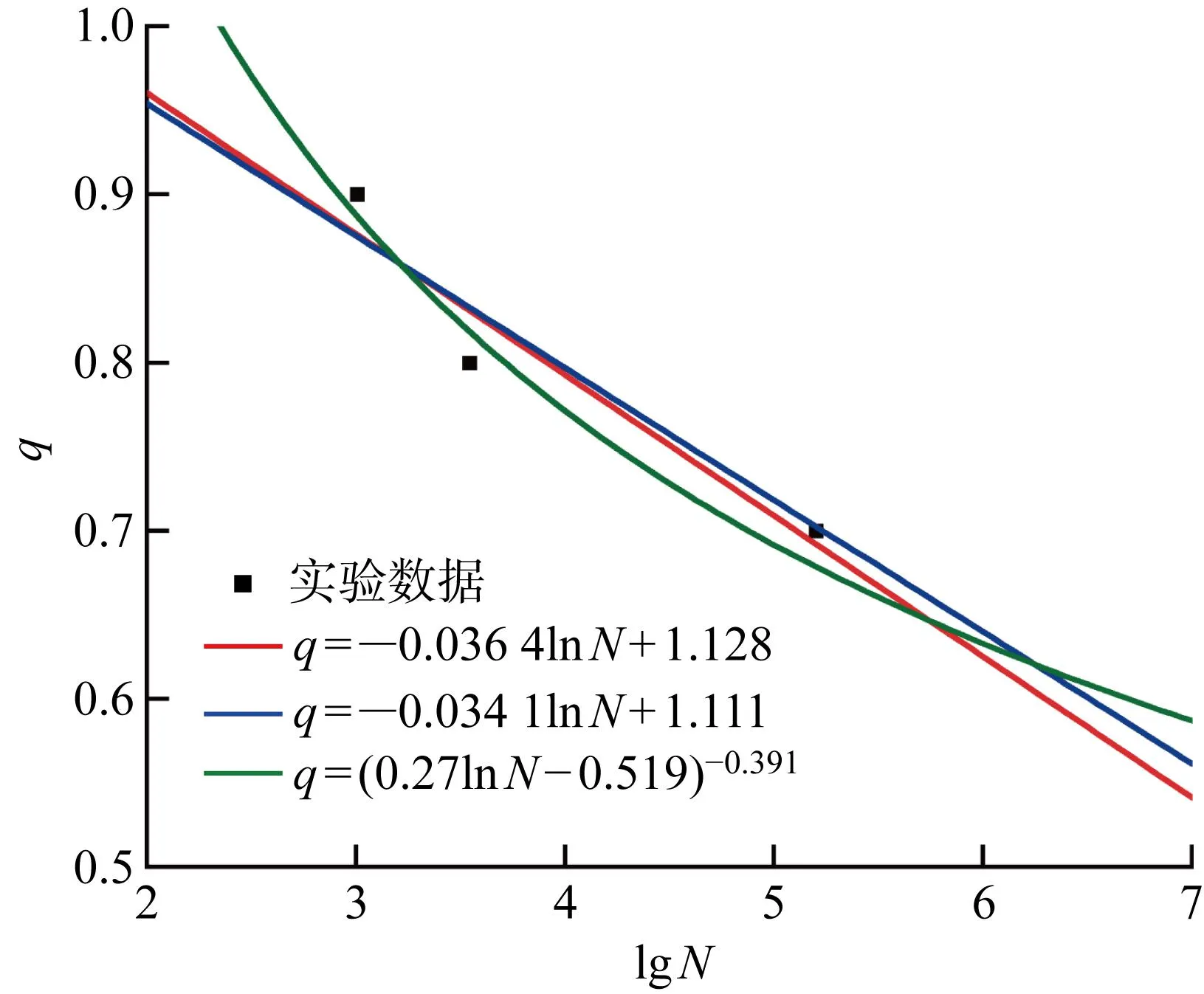
图2 3种建模方式拟合[90]20单向板的q-lg N曲线Fig.2 Fitting of [90]20 uni-directional plates q-lg N of three modeling methods

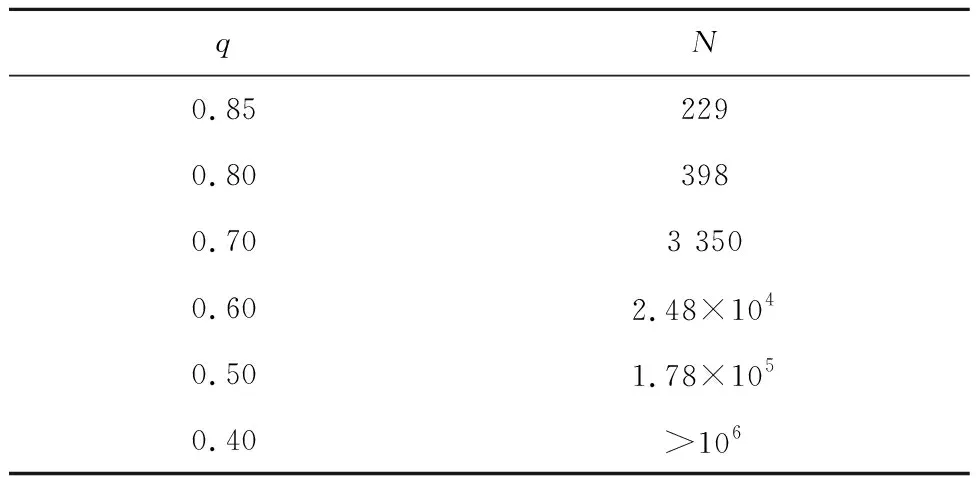
表5 [0/90]4s层压板在面内剪切应力作用下的疲劳实验数据(R=0.1)

q=-0.051 1lnN+1.117

(34)

q=(-0.042 0lnN+1.108)1.354

(35)

根据插值法,计算q=0.75,0.65,0.55时,N=1 874, 14 075, 101 400. 设原始序列为X(0)=[2293981 8743.35×1031.407 5×1042.48×1041.014×1051.59×105]. 根据式(16)～(23),计算一次累加序列和均值序列,C=381 930,D=323 897,E=5.252 9×1010,F=6.562 2×1010,a=-0.778 3.根据式(24)计算q=0.45,0.4,0.35时,N=1.399 7×106,3.048 4×106,6.638 8×106.基于这9组数据,用最小二乘法拟合双参数和三参数q-N函数,结果如下所示:

q=-0.046 2lnN+1.081

(36)

q=(-0.030 8lnN+1.082)1.956 9

(37)

将4种方法进行误差对比分析,结果如表6所示.

4种方法拟合q-lgN函数曲线,拟合结果如图3所示.

通过表6和图3可以发现,双参数q-N曲线的误差较小. 因此,本文在计算剪切损伤量时,选用双参数q-N曲线. 所以损伤函数为

(38)

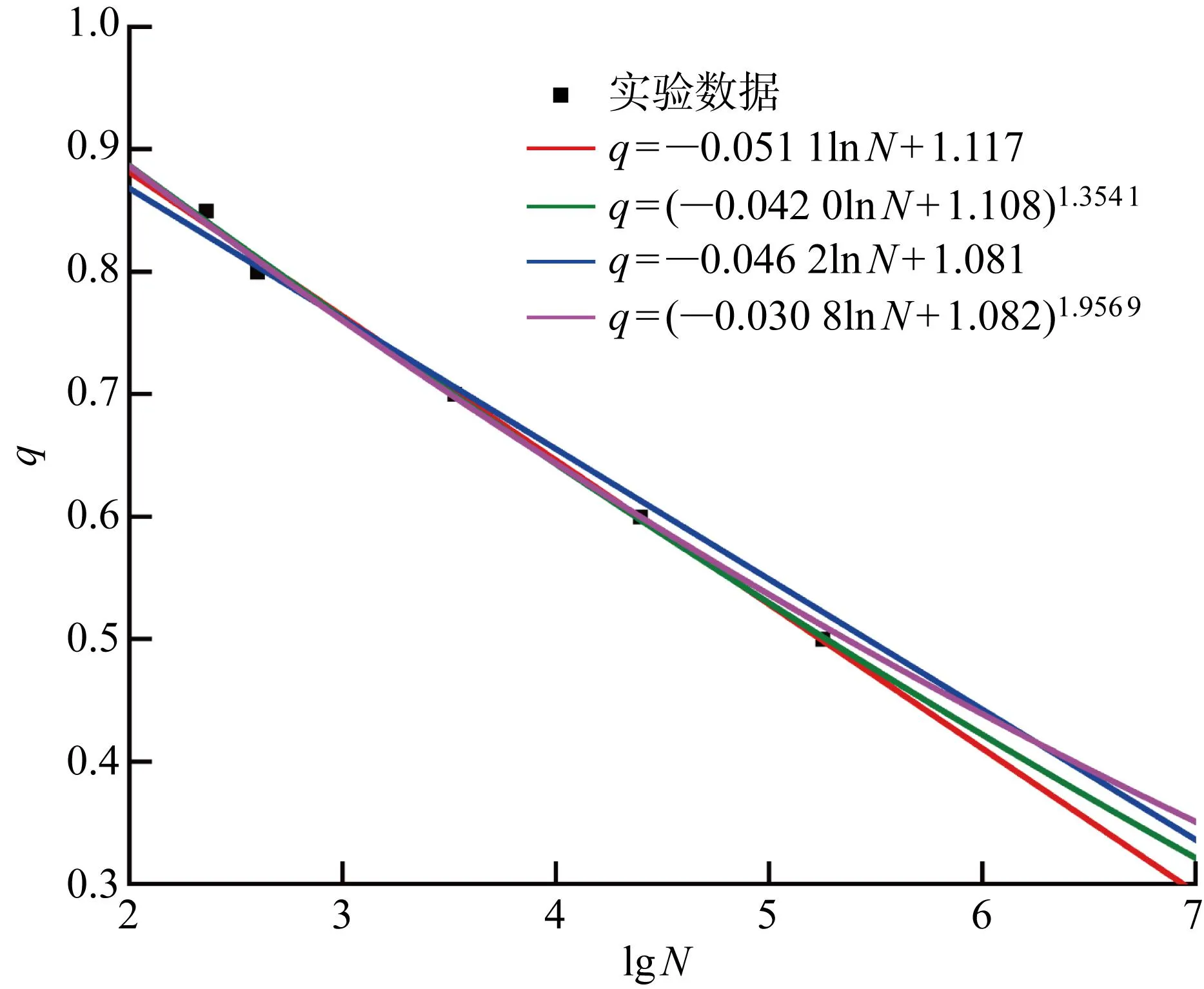
图3 4种建模方式拟合[0/90]4s层压板q-lg N曲线Fig.3 Fitting of q-lg N curves of the [0/90]4s laminate of four modeling methods

表6 拟合[0/90]4 s层压板q-N函数不同方法的精度对比Tab.6 Precision comparison of different methods for fitting [0/90]4 s laminate q-N function

2 FRP多向层压板的疲劳寿命

本文FRP层压板疲劳寿命预测的步骤为两大部分,第1部分是通过应力分析和失效分析,计算该层压板的拉伸强度. 第2部分是基于FRP层压板的拉伸强度和典型FRP单向板的疲劳寿命预测函数以及损伤函数来计算层压板的疲劳寿命. 对FRP层压板的疲劳寿命预测过程作如下假设:

(1) 多向层压板中的各单向板具有相同的疲劳性能,且层压板没有初始损伤[18].

(2) 把层压板的疲劳失效看成是不同单层逐次发生失效的间断过程,把材料性质的连续退化过程简化为单层的危险部位失效后,材料性质退化,应力分布改变.

2.1 FRP多向层压板的应力分析和失效分析

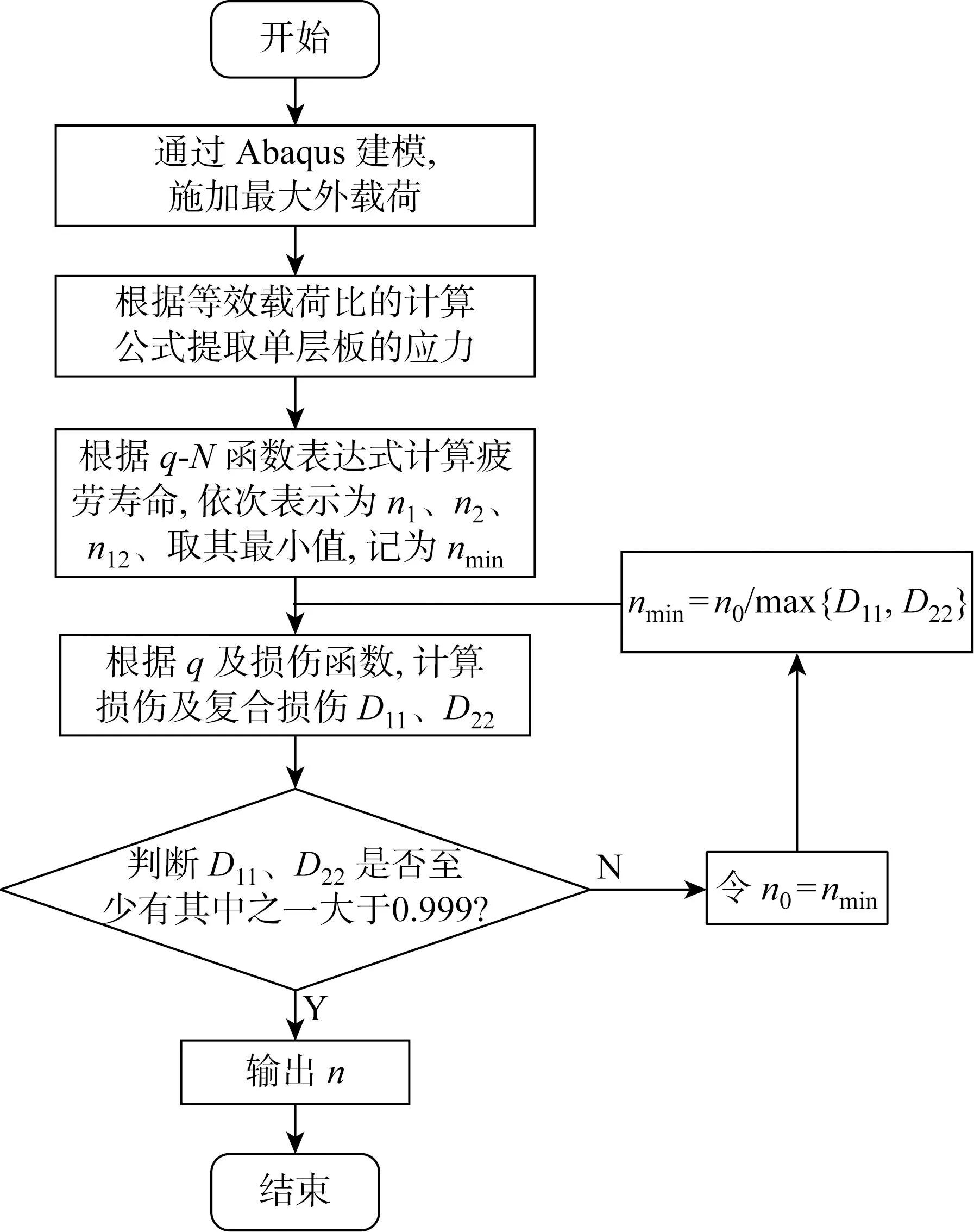
假设FRP层压板处于平面应力状态,利用Abaqus建模对层压板进行应力分析. 具体步骤如下.

(1) 通过Abaqus仿真拉伸实验,在加载外力P时,设定循环周期增量P,仅对Δn、Δ2n、Δ3n循环周期下的层压板进行应力分析和单元失效判断. 在Δn内只进行材料性能渐降,忽略性能突降. 选择合适的面内强度准则,判断是否失效. 本文选用Tsai-Hill强度准则[20]判定:

(39)

式中:σ11、σ22、τ12分别表示纵向、横向及剪切方向的应力.

(2) 计算单向板的失效强度.首先计算各单层的强度比RL,

(40)

找出最小强度比RLmin,强度比最小的单层为最先失效层. 然后计算该层的失效强度FS,

FS=PRLmin

(41)

根据Hashin失效准则,判断失效模式:

(42)

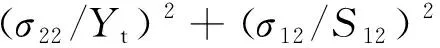
(43)

式中:S12为xy面内切应力.

若满足式(42)则为纤维拉伸失效,若满足式(43)则为基体拉伸失效. 若根据式(40)判断出该层已失效,判断失效模式时,两个都未达到失效,则根据相对大小判断失效模式,造成这种现象的原因是本文没考虑层间应力的影响.

(3) 对失效的单层进行刚度退化.本文采用Tsai提出的0.4Em刚度退化准则[21]:纤维断裂后,该层便不起作用了,其正轴模量矩阵Q退化为零矩阵,即Q11=Q22=Q12=Q66=0;基体的破坏退化规则为:纵向拉伸模量E11,泊松比ν12保持不变,横向拉伸模量E22下降至0.56E22,面内切变模量G12下降至0.

(4) 重复该过程,直到层压板失效,以单向板的失效强度最大值作为层压板的拉伸强度.

应力分析和失效分析的具体过程如图4所示.

2.2 FRP多向层压板的疲劳寿命

(1) 根据第1部分的结果得知层压板的极限拉伸强度SE,确定循环载荷的最大外载荷Pb:

Pb=SEq

(44)

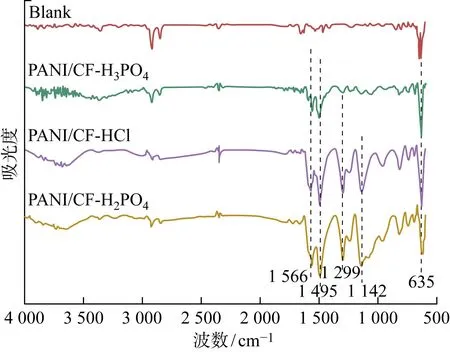
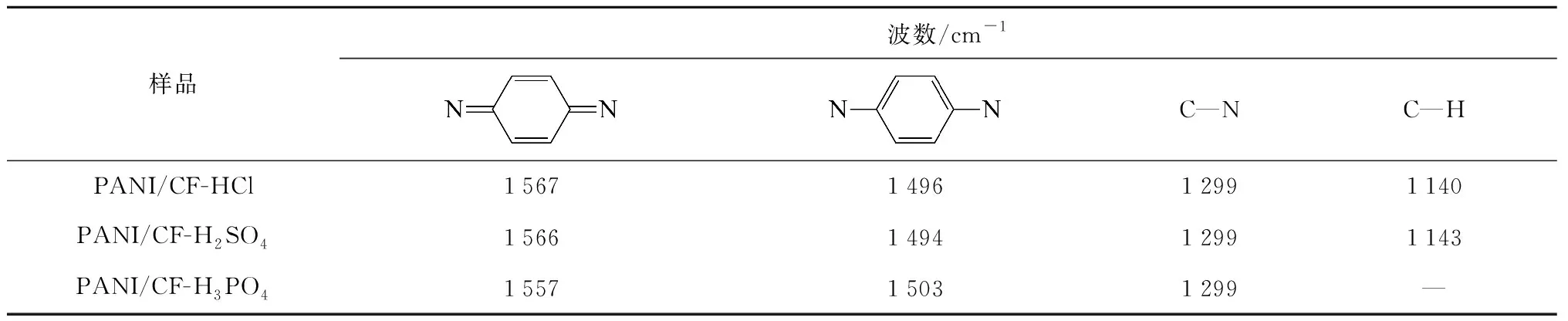
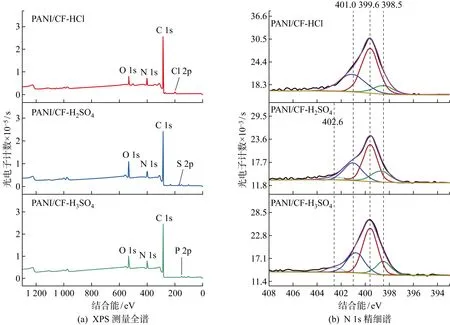
(2) 复合材料层压板在载荷加载时,失效层的破坏可能是静强度破坏或者疲劳破坏. 如果Pb>FS,属于静力破坏,发生静力破坏的单层也消耗了一定数量的疲劳寿命,计算等效的疲劳累积损伤. 如果发生纤维断裂,则将该层的累积损伤量D1、D2、D12均置为1,如果发生基体破坏, 将面内横向应力引起的累积损伤量D2置为1[18]. 若Pb

(4) 分别根据q-N函数表达式(28)、(31)、(36)计算其寿命n1、n2、n12,选择三者中最小的记为nmin,再根据损伤函数式(29)、(33)、(38)以nmin为初值进行迭代.

(5) 根据式(14)计算复合损伤D11、D22,判断D11、D22其中之一是否满足大于0.999,满足时迭代结束,若不满足,进行循环迭代,具体迭代方法如图5 所示. 迭代终值N为该单向板的疲劳寿命. 随后对该单向板根据其失效模式,进行刚度退化,即对材料属性进行改变. 因为材料的疲劳极限存在模糊性,累积损伤也不一定为1,所以当循环迭代时,n增加的缓慢时迭代结束,根据本文算例结果,将本文迭代终值复合损伤定义为0.999.

图5 层压板疲劳寿命计算Fig.5 Calculation of fatigue life of laminate

(6) 重复上述步骤,直到层压板失效.各单向板的累积寿命和为层压板的疲劳寿命.

3 实例验证与对比分析

材料T300/QY8911的弹性常数[22]纵向拉伸模量E11=135 GPa,横向拉伸模量E22=8.8 GPa,法向拉伸模量E33=8.8 GPa;泊松比ν12=0.33,ν23=0.48,ν13=0.33;Gij表示i-j面内切变模量,G12=4.47 GPa,G23=3.2 GPa,G13=4.47 GPa;强度参数[23]Xt=1 627.5 MPa,纵向压缩强度Xc=1 226 MPa,Yt=68.4 MPa,横向压缩强度Yc=218 MPa,Sin=89.9 MPa.

3.1 算例1

层压板的铺层方式为[0/90]4s,长40 mm,宽20 mm,单层厚度为0.125 mm[23].根据材料的弹性参数和强度参数,采用Abaqus建立分析计算模型,R=0.1,q=0.85.为了提高计算精度,网格沿宽度方向从边界向中间由密变疏,对网格划分进行收敛性分析以及网格无关性检查,最终确定有限元模型的网格大小是:两端是边长为0.5 mm的正方体,中间是边长为1 mm的正方体. 单元所用类型为Continum shell: SC8R,单元数量为 9 600,所建有限元模型如图6所示,铺层方式如图7所示.图中:Angle=0表示该单向板铺层角为0°,即单向板铺层的纵向与层压板参考坐标X轴之间的夹角为0°,Angle=90表示该单向板铺层角为90°;Ply-1—Ply-16分别表示该层压板的铺层,共有16层.

图6 [0/90]4s层压板的模型Fig.6 Model of [0/90]4s laminate

图7 [0/90]4s的铺层方式Fig.7 Laying method of [0/90]4s laminate

在层压板左侧端面施加完全约束,在层压板右侧端面施加均布力载荷. 然后施加载荷,当P逐渐增加到560 MPa时:90°铺层危险点的应力分布为σ11=-6.271 MPa,σ22=68.34 MPa,τ12=4.644 MPa. 根据式(39)判断该层是否失效:

1.001 1>1

(45)

根据式(45)结果大于1,所以90° 铺层失效,该层的失效强度比RL(90°)=0.999 5,失效强度FS(90°)=559.72 MPa. 根据失效准则判断该层的失效模式为基体失效. 0° 铺层危险点的应力分布为σ11=1 096 MPa,σ22=19.93 MPa,τ12=13.93 MPa. 判断该层是否失效:

0.554 2<1

(46)

根据式(46)结果小于1,因此0°铺层未失效. 所以对90°铺层根据本文选定的刚度退化准则进行刚度退化. 然后施加载荷,当载荷增加到738 MPa时:0°铺层危险点的应力分布为σ11=1 464 MPa,σ22=29.8 MPa,τ12=12.27 MPa. 判断该层是否失效:

1.001 1>1

(47)

由式(47)计算结果大于1,因此0°铺层失效,该层的失效强度比RL(0°)=0.999 4,失效强度FS(0°)=737 MPa,失效模式为纤维断裂. 极限强度SE=737 MPa,根据式(44),计算循环载荷的最大外载荷,Pb=SEq=626.5 MPa. 因为FS(90°)Pb,因此,0°铺层因为疲劳破坏而失效.

(48)

D11>1,则该单向板的寿命为2.330 6×105. 因此,该层压板的疲劳寿命为2.331 06×105. 根据文献[23],该层压板的疲劳寿命实验数据为 2.33×105,将本文预测结果、多个文献方法与实验数据计算相对误差,结果进行对比,如表7所示.

表7 不同方法预测[0/90]4s层压板的疲劳寿命结果对比

3.2 算例2

层压板的铺层方式为[-60/0/60]3s,其在Abaqus建模时,材料属性、模型尺寸、网格划分、单元类型以及加载方式均与算例1一致,q=0.8. 施加载荷,当P逐渐增加到320 MPa时:-60° 铺层危险点的应力分布为σ11=-160.3 MPa,σ22=64.17 MPa,τ12=29.98 MPa. 判断该层是否失效:

1.004 9>1

(49)

根据式(49)的计算结果大于1,因此-60°铺层失效,失效强度比RL(-60°)=0.997 5,失效强度FS(-60°)=319.2 MPa,失效模式是基体破坏. 60°铺层危险点的应力分布为σ11=-160.9 MPa,σ22=64.14 MPa,τ12=29.92 MPa. 判断该层是否失效:

1.003 8>1

(50)

根据式(50)的计算结果大于1,因此60°铺层失效,失效强度比RL(60°)=0.998 1,失效强度FS(60°)=319.4 MPa,失效模式是基体破坏. 0°铺层危险点的应力分布为σ11=1 235 MPa,σ22=8.705 MPa,τ12=20.93 MPa. 判断该层是否失效:

0.642 2<1

(51)

根据式(51)的计算结果小于1,因此0° 铺层未失效. 对 -60° 和60° 铺层,根据本文选定的刚度退化准则进行刚度退化,然后施加载荷,当载荷增加到350 MPa时:0° 铺层危险点的应力分布为σ11=1 558 MPa,σ22=10.06 MPa,τ12=26.25 MPa. 判断该层是否失效:

1.017 4>1

(52)

表8 不同方法预测[-60/0/60]3s层压板的疲劳寿命结果对比

4 结论

复合材料层压板内部损伤会引起刚度退化,而损伤不断累积会导致其疲劳破坏. 以疲劳模量为参量,借助灰色系统构造FRP单向板的损伤函数和疲劳寿命函数,通过建模对FRP层压板有限元分析,对其疲劳破坏过程模拟. 这种理论与仿真结合预测FRP多向层压板疲劳寿命的方法可以得到以下结论:

(1) 通过灰色系统GM(1, 1)模型建模,拟合了q-N函数表达式以及损伤函数表达式,且拟合结果与最小二乘法拟合的结果相比提高了预测精度,拟合的疲劳寿命和损伤函数可直接用于同种材料任意铺层的多向层压板的寿命预测.

(2) 基于Abaqus模拟仿真,对多层板进行应力分析和失效分析,然后与建立的q-N函数结合,以此来预测FRP多层板的疲劳寿命. 该方法与传统的经典层压板理论做应力分析的方法相比减小了误差. 因为经典层压板理论认为,单层板的应力分布是均匀的,但事实上,受力点与受力方向都会使单层板存在危险点,而通过Abaqus建模,可以解决这个问题.

(3) 本文理论与模拟仿真紧密结合的方法突破了以往完全依赖试件疲劳试验或者只有仿真的预测方法. 通过算例验证,证明了该方法的有效性,具有一定的工程应用价值.

附录