基于极限学习机模型参数优化的光伏功率区间预测技术

2024-03-28何之倬黄琬迪张沈习程浩忠

上海交通大学学报 2024年3期

何之倬, 张颖, 郑刚, 郑芳, 黄琬迪, 张沈习, 程浩忠

(1. 国网上海市电力公司青浦供电公司,上海 201700; 2. 上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240)

为缓解日益突出的能源和环境问题,太阳能光伏(Photovoltaic, PV)作为一种资源丰富、安全可靠、环境友好的可再生能源,近年来得到大力发展[1].由于光伏发电系统仅在白天有出力,且受到气象因素变化的影响,所以光伏出力具有一定波动性和随机性[2].光伏在电网中渗透率的增加可能会对电力系统的潮流分布、暂态特性、电能质量等产生不利影响,使电网的运行与控制面临挑战[3].对光伏功率进行准确预测有助于调度部门调整含PV电力系统的运行方式,以维持电力系统的安全稳定[4].

目前,基于数据驱动的方法是使用最广泛的光伏功率预测方法,它可避免复杂的物理建模过程,从大量历史数据中获取光伏功率出力与外界因素之间的联系.时间序列法[5-6]、回归分析法[7-8]、人工智能法[9-11]等都属于基于数据驱动的预测方法.

依据预测结果的形式,光伏功率预测分为点预测和区间预测.点预测是一种确定性预测,结果较为直观,但是难以表征光伏出力的不确定性;区间预测可以得到一定置信度水平下光伏功率的上下限,对于含光伏电力系统的风险评估、不确定性评估具有重要参考价值.Delta法[12-13]是一种构造预测区间的方法,需假定数据噪声同质且满足标准正态分布;事实上,噪声在很多情况下难以满足这个假设,因此Delta法得到的预测区间与实际情况可能有较大差距.文献[14-15]中使用贝叶斯法构造预测区间,但是Hessian矩阵的求取使得此方法的计算负担过重.文献[16-17]中使用Bootstrap法进行区间预测,得到认知不确定性和偶然不确定性分别对应的预测区间后进行叠加,其结果可以表征总体不确定性;Bootstrap法虽易于实现,但当数据样本较多时,计算效率低.边界估值(Lower Upper Bound Estimation, LUBE)理论[18]根据预测区间评估指标,利用启发式算法对神经网络参数进行寻优,可以得到满足可信度和准确度要求的神经网络区间预测模型.文献[18]中通过多个算例分析说明:与Delta法、贝叶斯法、Bootstrap法相比,LUBE法得到的区间预测模型性能更为稳定,且预测区间可信度较高.传统前馈神经网络多采用梯度下降法,训练时间较长,容易陷入局部最优,且学习率具有选择敏感的特点.极限学习机(Extreme Learning Machine, ELM)可克服上述缺陷,具有更快的学习速度和更优的泛化能力,被广泛应用于预测领域[19].文献[20]中使用ELM模型来进行光伏电站功率区间预测,ELM模型隐层输入权重与偏置可以随机生成,而隐层输出权重通过求解最优化问题确定,进而得到预测区间.然而,ELM模型也存在缺点[21]:当数据样本自变量过多时,模型的稳定性与泛化能力会受到不利影响;原始数据集中若存在离群点,可能会导致模型预测性能不佳;此外,模型的隐层输入权重与偏置参数随机生成,其预测精度仍有提升空间.

针对现有研究存在的问题,提出一种考虑ELM训练集优化与参数寻优的光伏功率区间预测技术.利用相关性分析对ELM的输入参数进行筛选,剔除无关历史信息,仅保留与因变量具有较高相关性的自变量;提出基于加权欧氏距离指标的ELM训练集选取方法,在去除异常离群点、提高训练效率的同时,使得训练集样本和待预测样本具有较高的相似度,从而避免过拟合,提升预测的可信度和准确度;提出一种ELM参数混合寻优算法,在根据预测区间评估与优化准则设定适应度函数后,采用精英保留策略遗传算法(Elitist Strategy Genetic Algorithm, ESGA)优化ELM隐层的输入权重与偏置取值,同时使用分位数回归方法优化ELM的隐层输出权重,生成评价指标最优的预测区间,有效降低模型预测随机性.将提出的预测方法应用于实际算例,并与其他方法进行比较,以证明本文方法在光伏功率区间预测上的优越性.

1 光伏功率区间预测

1.1 光伏功率预测区间定义

光伏功率是一个随机变量,利用区间预测可以得到其在一定条件下的取值区间,在工程实际中比点预测具有更高参考价值.

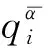
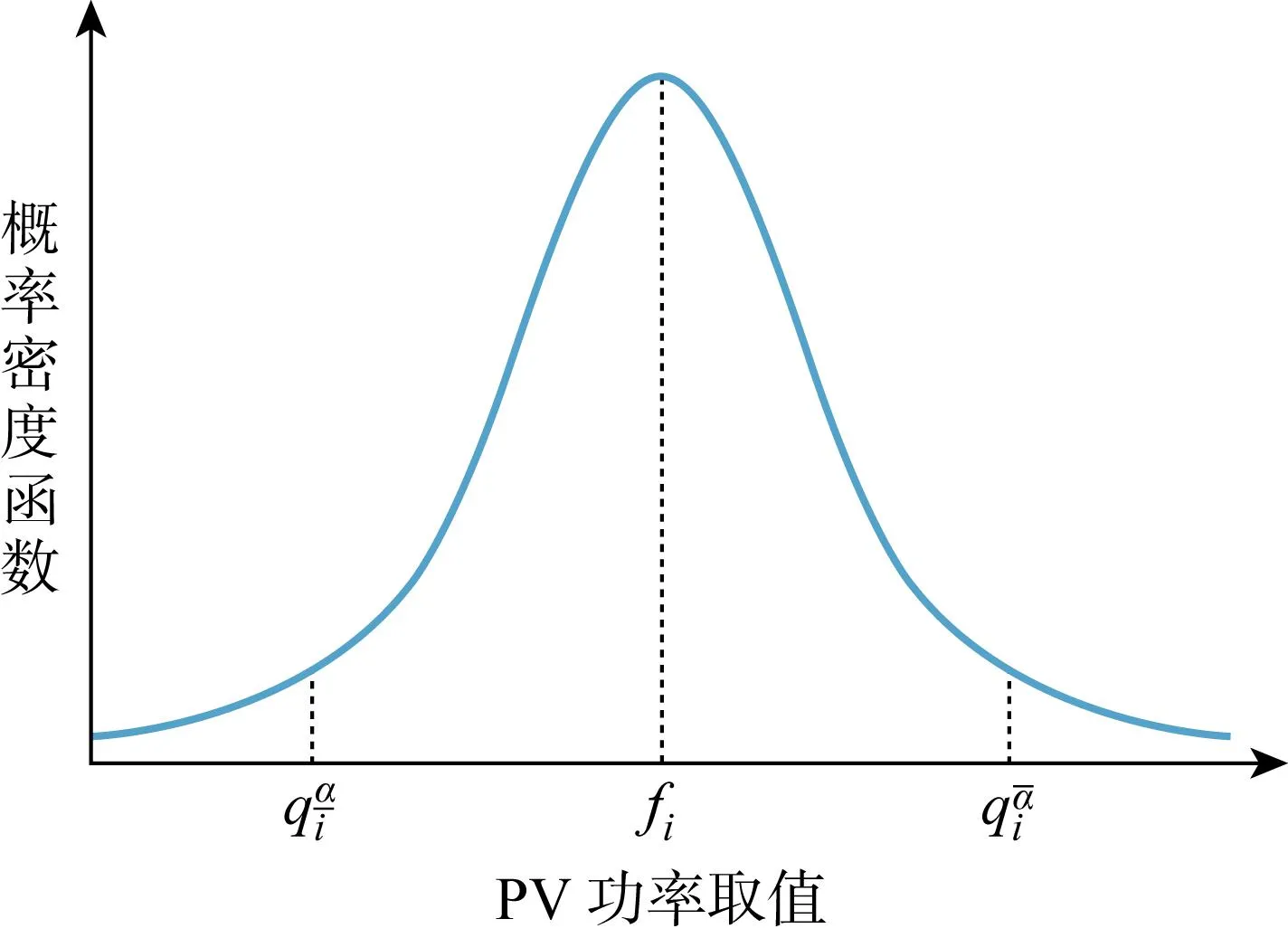
图1 PV功率概率密度函数Fig.1 Probability density function of PV power

(1)

式中:Pr(·)为概率;fi为预测的变量值.

1.2 光伏功率预测区间评估指标

分别采用可信度与准确度衡量区间预测性能.首先,预测区间覆盖率(Prediction Interval Coverage Probability, PICP)可以表征预测区间可信度,即

(2)

此外,如果PICP非常高,但是预测区间宽度非常大,则区间预测结果没有参考价值.预测区间归一化平均带宽(Prediction Interval Normalized Average Width, PINAW)可以表征预测区间准确度,即

(3)

在PINC一定的情况下,PINAW越小,说明预测区间平均宽度越窄,准确度越高.

2 ELM

2.1 ELM原理

ELM是一种单层前馈神经网络,于2004年由Huang等[23]提出.ELM的隐藏层输入权重和偏置可以随机生成,唯一需要确定的是隐藏层输出权重.与传统前馈神经网络相比,ELM运算效率非常高,且具有优越的泛化性能[24].

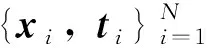
图2 ELM结构Fig.2 Structure of ELM

(4)

式中:yi=[yi1yi2…yim]T∈Rm为第i个训练样本的输入xi经ELM处理后的输出;βj=[βj1βj2…βjm]T∈Rm为第j个隐藏层神经元的输出权重;g(·)为激励函数;ωj=[ωj1ωj2…ωjn]T∈Rn为第j个隐藏层神经元的输入权重;bj为第j个隐藏层神经元的偏置.

由于ELM能够以极小误差逼近训练样本,所以训练样本的目标输出可表示为

(5)

相应的矩阵形式为

T=Hβ

(6)

式中:T∈RN×m为目标输出矩阵;H∈RN×L为隐藏层输出矩阵;β∈RL×m为隐藏层输出权重矩阵.

当隐藏层输入权重和偏置生成后,H为常数矩阵.因此,β的求解可以视为求解线性系统的最小二乘特解问题,即寻找β的最优值使代价函数,ELM模型输出和目标输出之差的模最小,如下式所示:

(7)

由广义逆理论可得,β的最小二乘特解可以表示为

β*=H†T

(8)

式中:H†为H的Moore-Penrose广义逆.

ELM被广泛应用于基于数据驱动的变量预测,并能取得较为理想的预测结果.在训练前,通常将样本数据归一化,并使用ELM预测光伏电站功率.

2.2 ELM参数优化与预测区间生成

为了使ELM区间预测获得更优结果,从两个方面对ELM进行改进.第一,提出加权欧氏距离指标,对历史样本进行筛选以获得ELM训练集,使得训练集样本和待预测日各时刻的样本具有较高程度的相似性;第二,提出ELM参数混合寻优算法,使用ESGA对ELM隐藏层输入权重ωhid与偏置bhid进行寻优,在每次迭代中,对于给定的ωhid和bhid,选取分位数回归方法优化ELM隐藏层输出权重的参数值和对应预测区间,并计算个体适应度,最终确定使ELM预测性能最优的隐藏层输入权重与偏置值.

2.2.1ELM训练集选取提出加权欧氏距离指标来衡量待预测样本与历史样本自变量数值之间的相似度.加权欧氏距离越小,表示相似度越高.为充分考虑不同自变量对因变量影响程度的差异性,首先应进行相关性分析.考虑光伏出力数据具有周期性等特征,采用Spearman相关系数描述数据间相关程度.根据定义,变量x与y间的Spearman相关系数计算如下:

r(x,y)=

(9)

解读概念语法隐喻 …………………………………………………………………………………… 杨波（6.30）

变量间距离度量方面,传统欧氏距离主要计算变量间的真实距离,描述样本间不相似程度.对应元素较多时,为充分考虑各元素对累积相似性的影响,可采用加权欧氏距离描述气象特征对光伏出力的影响情况.设x1,x2, …,xns是ns个对因变量影响较大的自变量,Spearman相关系数分别为r1,r2, …,rns,对于气象因素与光伏功率时间序列,采用Spearman相关系数确定权值,并定义样本之间的加权欧氏距离如下:

(10)

式中:hi为历史数据中某样本单元的自变量数值向量;xp为某待预测样本单元的自变量预报值向量;1/ωk为自变量k的权重,Spearman相关系数绝对值越大,ωk越大,距离权重赋值越小.ωk的计算公式如下:

(11)

加权欧氏距离可充分考虑各因素对累积相似性的重要程度,通过各因素相关性决定变量权值系数,使变量间的欧氏距离标准化.对于待预测的各样本单元,在历史数据中筛选与其加权欧氏距离最小的若干个样本单元,构成最终的ELM训练集.

2.2.2ELM隐藏层输入权重与偏置混合寻优由于ELM的参数会对其预测性能产生影响,而随机生成的ELM隐藏层输入权重与偏置可能导致预测模型无法获得最优的预测区间,所以有必要确定ELM参数的最优值.生成ELM训练集后,将 ESGA 与分位数回归相结合,对ELM的隐藏层输入权重与偏置进行混合寻优.

预测区间的优化需要构建相应准则,以判断个体的优劣.综合考虑PICP和PINAW,定义适应度函数为

ffit(ωhid,bhid)=-(β(ωhid,bhid)M×|dACE(ωhid,bhid)|+pPINAW(ωhid,bhid))

(12)

式中:β(ωhid,bhid)为布尔类型指示函数,其具体数值由隐藏层输入权重及偏置矩阵决定,当pPINC>pPICP时,β(ωhid,bhid)=0,否则,β(ωhid,bhid)=1;M为惩罚系数,此时取较大值;平均覆盖率误差是PINC和PICP的差值,用dACE(ωhid,bhid)表示.

ESGA优化ELM隐藏层输入权重与偏置具体流程可概括如下:

(1) 生成mc个待优化隐藏层输入权重及偏置组合(ωhid,bhid),构成初始种群.

(2) 根据适应度函数ffit(ωhid,bhid)计算结果进行个体评价,其中适应度最高的mcfit个个体(ωhid,bhid)保留为精英个体.

(3) 除精英个体外,通过选择、交叉、变异等遗传操作构建新的子代种群,并计算子代个体适应度.

(4) 用保留的精英个体替换子代种群中适应度最低的个体,并将精英个体更新为子代种群中适应度最高的mcfit个个体.

(5) 若达到最大迭代次数,则退出循环,输出最优个体对应的隐藏层权重与偏置参数;否则,返回步骤(3).

在ESGA的每一次迭代中,对于每个个体对应的ELM隐藏层输入权重与偏置,利用分位数回归法得到ELM隐藏层输出权重最优值与预测区间,然后计算个体适应度.个体适应度越大,说明相应ωhid和bhid的取值越优,ELM的区间预测性能越优.

2.2.3预测区间生成通常情况下,历史数据中仅包含随机变量的观测值,而不含取值区间上下限,无法通过直接训练ELM对变量的取值区间进行预测.因此,采用分位数回归理论[25]生成光伏出力预测区间.

对于随机变量yrand,分布函数用F(yrand)表示.yrand的第τ分位数定义为

F-1(τ)=inf{yrand:F(yrand)≥τ}

(13)

式中:τ是位于0～1之间的数;inf{·}表示变量的下确界.

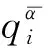
(14)

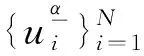
(15)

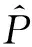
3 光伏功率区间预测流程

3.1 数据获取

基于数据驱动的光伏功率预测需要分析大量历史数据,通过模型训练来构建光伏功率与外部因素之间的关系.已有研究表明光伏功率特性存在季节性变化特征,即不同季节对应的光伏功率预测模型有差异[26].确定待预测日的日期后,需要分别从光伏站和气象站获取此季节各个时刻的光伏功率数据与气象历史数据,构成历史样本单元.

3.2 数据预处理

获得历史样本单元后,需要对数据进行预处理,得到可供模型训练的数据集.第一,剔除存在缺失或异常数据点的历史样本单元,以免对模型训练造成不利影响.第二,使用Spearman相关系数量化气象因素对光伏功率的影响程度,从中筛选出与光伏出力相关性较高的气象因素作为ELM的输入.第三,基于Spearman相关系数值,根据式(10)～(11)计算待预测日样本单元与历史样本单元间的加权欧氏距离;对于待预测日的每个时刻,选取与其相距最近的若干个历史样本单元,共同构成ELM的训练集.

3.3 模型训练

确定训练集后,需要进行模型训练.首先,应确定ELM的结构.通过相关性分析确定n个与光伏出力具有较高相关程度的气象因素后,相应地,ELM输入层的神经元个数为n;因ELM的输出是光伏功率上下限,故输出层神经元个数为2;隐藏层神经元个数的选取需要保证预测模型的回归性能稳定,不能过少,同时也应当避免过多,否则会加重计算负担,且对提升ELM预测性能无益.交叉验证法[27]是一种常用的确定神经网络结构的方法,采用此法确定ELM的隐藏层神经元个数:将ELM训练集样本随机均分为5个部分,对同一隐藏层神经元个数,依次取其中4个部分进行训练以确定ELM区间预测模型,并将最后一部分评估最终区间预测性能,然后将5次预测区间评估指标取均值.分析不同隐藏层神经元数量下预测区间评估指标均值,便可以确定隐藏层神经元数目优化结果.优化ELM结构之后,为了获得使模型预测性能最佳的ELM参数,使用 ESGA 和分位数回归对ELM进行参数寻优,确定ELM隐藏层输入权重与偏置的最优值,形成ELM预测模型.

3.4 区间预测

得到ELM预测模型后,输入待预测日各时刻经相关性分析筛选后的气象因素预报值,通过分位数回归,获得相应置信水平下光伏功率的预测区间.

4 算例分析

4.1 数据介绍

为验证所提光伏功率区间预测方法的适用性,选取2018年澳大利亚昆士兰大学露西亚校区的光伏出力数据与气象站数据进行算例分析.光伏装机容量为433 kW,监测的气象因素包括风向角、风速、温度、相对湿度、海平面气压、降雨量和太阳辐照度.光伏功率和气象数据的采样间隔均为1 min.光伏在夜晚出力恒为0,仅对白天光伏出力大于0的时刻进行光伏功率区间预测,选取时间步长为15 min[27].在指定光伏功率待预测日后,通过对之前若干邻近日光伏出力起止时刻的拟合分析,可确定待预测日中光伏出力大于0的时间段.

剔除历史数据中数据缺失或异常的样本后,分别计算四季光伏功率与各项因素的Spearman相关系数.根据相关系数绝对值的计算结果,太阳辐照度与光伏功率相关系数绝对值为最高水平,始终维持于0.96以上;四季相对湿度与光伏功率相关系数绝对值分布于0.46～0.66;温度与光伏功率相关系数绝对值分布于0.39～0.60,略低于相对湿度;其他因素如风向角、风速等与光伏功率的相关系数绝对值总体维持较低水平,低于0.2,因此该类因素的影响忽略不计.

由于光伏出力特性与天气类型相关[28],为测试所提预测方法在各种天气类型下是否均能实现高性能的光伏功率区间预测,选择2018年7月1日(阴雨天)、8月3日(多云天)和9月10日(晴天)的数据,分别在PINC为95%、90%、85%和80%的情况下预测光伏功率区间,并计算指标值评估预测结果.2018年夏季(6～8月)与秋季(9～11月)数据中分别剔除7月1日、8月3日与9月10日数据后,作为3次区间预测中ELM训练集的待选集.对于待预测日的每一个样本单元,计算其与待选训练集中每一个样本单元的加权欧氏距离,选取其中相似度最高的50个样本单元,组成ELM训练集.

4.2 预测结果

考虑到光照时间,对于7月1日、8月3日、9月10日3个典型日,确定ELM训练集后,需要通过交叉验证选取ELM隐藏层神经元数量.交叉验证结果如图3(a)～3(c)所示.由于交叉验证时ELM隐藏层输入权重与偏置的生成是随机的,所以得到的预测区间并非最优区间,但评估指标随ELM隐藏层神经元个数增加所呈现的变化趋势可以为隐藏层神经元个数的选取提供重要依据.由图3可知,在各情况下,当隐藏层神经元个数达到20后,ELM的预测性能趋于稳定.因此,在算例分析中选用的隐藏层神经元节点数为20.

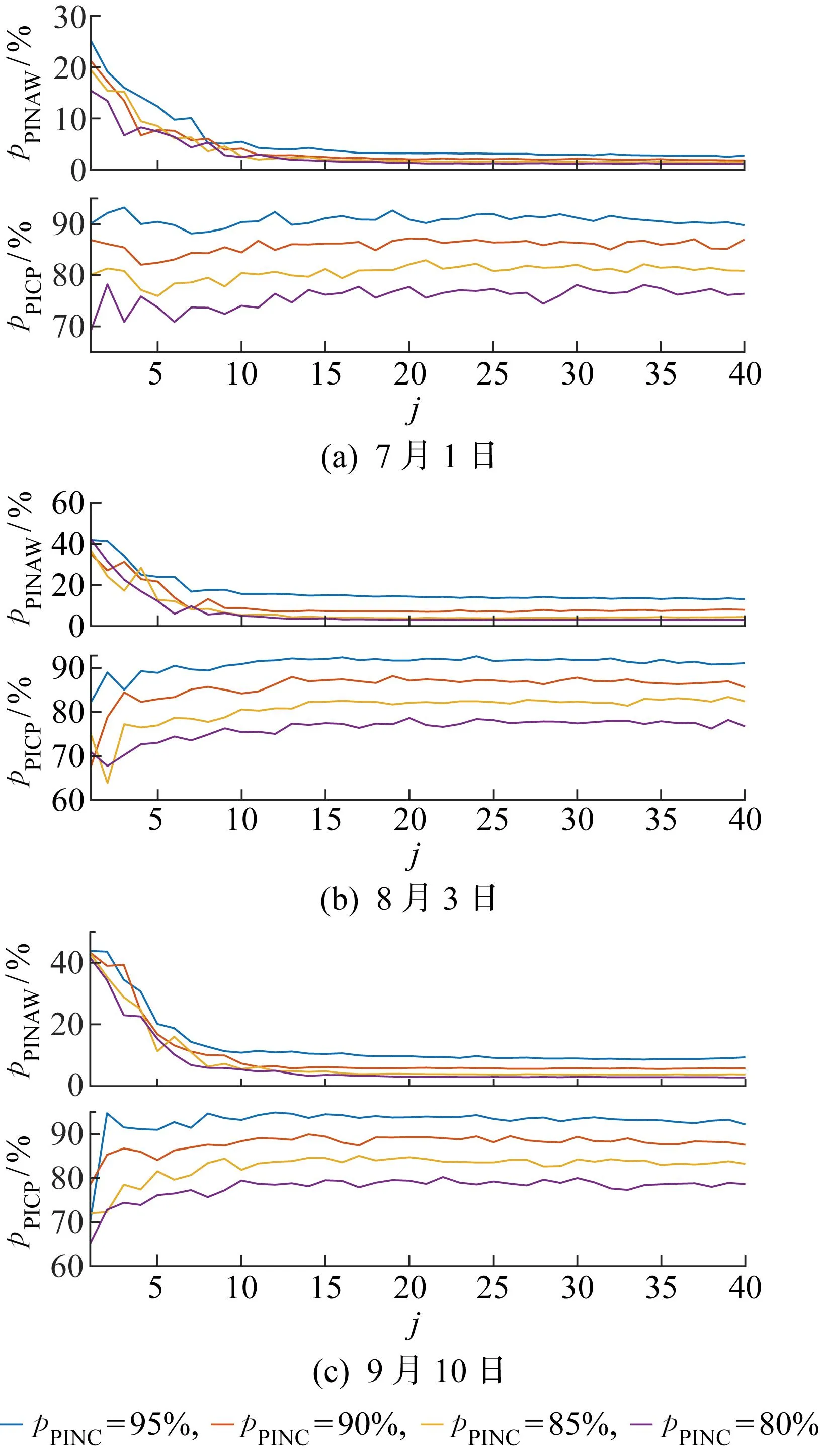
图3 交叉验证结果Fig.3 Results of cross validation

4.2.1阴雨天区间预测结果 7月1日6:30—17:00 在PINC分别为95%、90%、85%、80%的4种场景下的光伏电站功率区间预测结果如图4所示.7月1日的预测区间评估指标值如表1所示.

图4 不同PINC下7月1日预测区间Fig.4 Prediction intervals on July 1 at different PINCs

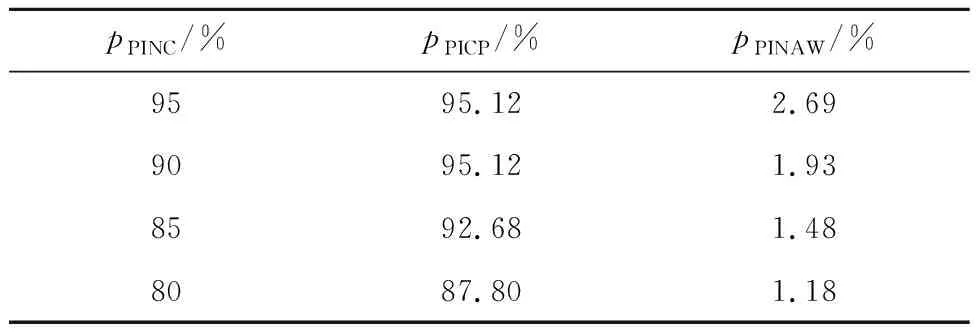
表1 7月1日预测区间评估指标Tab.1 Assessment of prediction intervals on July 1

4.2.2多云天区间预测结果 8月3日 6:45—17:15 在PINC分别为95%、90%、85%、80%的4种场景下的光伏电站功率区间预测结果如图5所示.8月3日的预测区间评估指标值如表2所示.

图5 不同PINC下8月3日预测区间Fig.5 Prediction intervals on August 3 at different PINCs

表2 8月3日预测区间评估指标Tab.2 Assessment of prediction intervals on August 3

4.2.3晴天区间预测结果 9月10日 6:15—17:30 在PINC分别为95%、90%、85%、80%的4种场景下的光伏电站功率区间预测结果如图6所示.9月10日的预测区间评估指标值如表3所示.

图6 不同PINC下9月10日预测区间Fig.6 Prediction intervals on September 10 at different PINCs

表3 9月10日预测区间评估指标Tab.3 Assessment of prediction intervals on September 10

4.2.4光伏功率区间预测结果分析从图4～6可以看出,光伏功率在不同天气类型下呈现出不同特性.阴雨天太阳辐照度较小,光伏功率也较小;多云天的光伏功率也可能具有较大峰值,但由于云层移动和遮挡,光伏功率曲线存在剧烈波动;晴天的光伏功率曲线较为平滑,且峰值较大.在3种天气类型下,预测区间上下限的变化趋势和实际光伏功率变化趋势均能保持一致.随着PINC减小,图4～6中预测区间覆盖率降低,且预测区间宽度也变小.表1～3中PICP与PINAW的数值更加直观地描述了这一现象.数据显示,在3种天气类型下,本文方法得到的光伏功率区间预测结果均能满足可信度要求,即PICP均高于PINC.以8月3日为例,PINC为95%及90%对应的预测区间能够完全覆盖预测时间段内实际的光伏功率点,PICP高达100%,而95%预测区间是4种置信水平下最宽的,PINAW达到12.87%,意味着预测结果可信度高,但较为保守.将PINC由95%减小为80%,实际的PICP也在逐渐减小;在牺牲预测区间可信度的同时,预测区间准确度提高,PINAW最小可以低至3.03%.在PINC取值不同的情况下,预测区间的可信度均满足置信水平要求,PICP明显高于PINC.

4.3 不同区间预测方法结果对比

为验证本文光伏功率区间预测方法的优越性,使用其他预测方法对同一算例进行光伏功率区间预测.各方法说明如下:

(1) 方法 I 为本文所提光伏功率区间预测法.

(2) 方法 II 使用普通欧氏距离指标对ELM训练集进行选取,即式(10)中距离权重恒为1,其他步骤均与方法I相同.

(3) 方法 III 不含基于加权欧氏距离指标的ELM训练集选取这一步骤,其他步骤均与方法 I 相同.

(4) 方法 IV 为ELM模型的隐藏层输入权重与偏置随机生成,其他步骤均与方法I相同.

方法 I 与方法 II、方法 III、方法 IV 的对比可以分别体现出加权欧氏距离指标、ELM训练集选取以及隐藏层输入权重与偏置优化对预测区间性能的影响.考虑到方法 IV 中ELM隐藏层输入权重与偏置的随机性,使用方法 IV 进行10次ELM训练,并取10次预测区间评估指标的期望值与其他方法的结果进行对比.

由于历史数据样本庞大,为避免训练时间过长,同时为了控制训练集相同,以排除无关因素的影响,方法 IV 的训练集由本文提出的加权欧氏距离指标确定.方法 III 的训练集在历史样本单元中随机抽样生成,且训练集样本规模与其他方法相同.不同方法区间预测结果对比如表4所示.

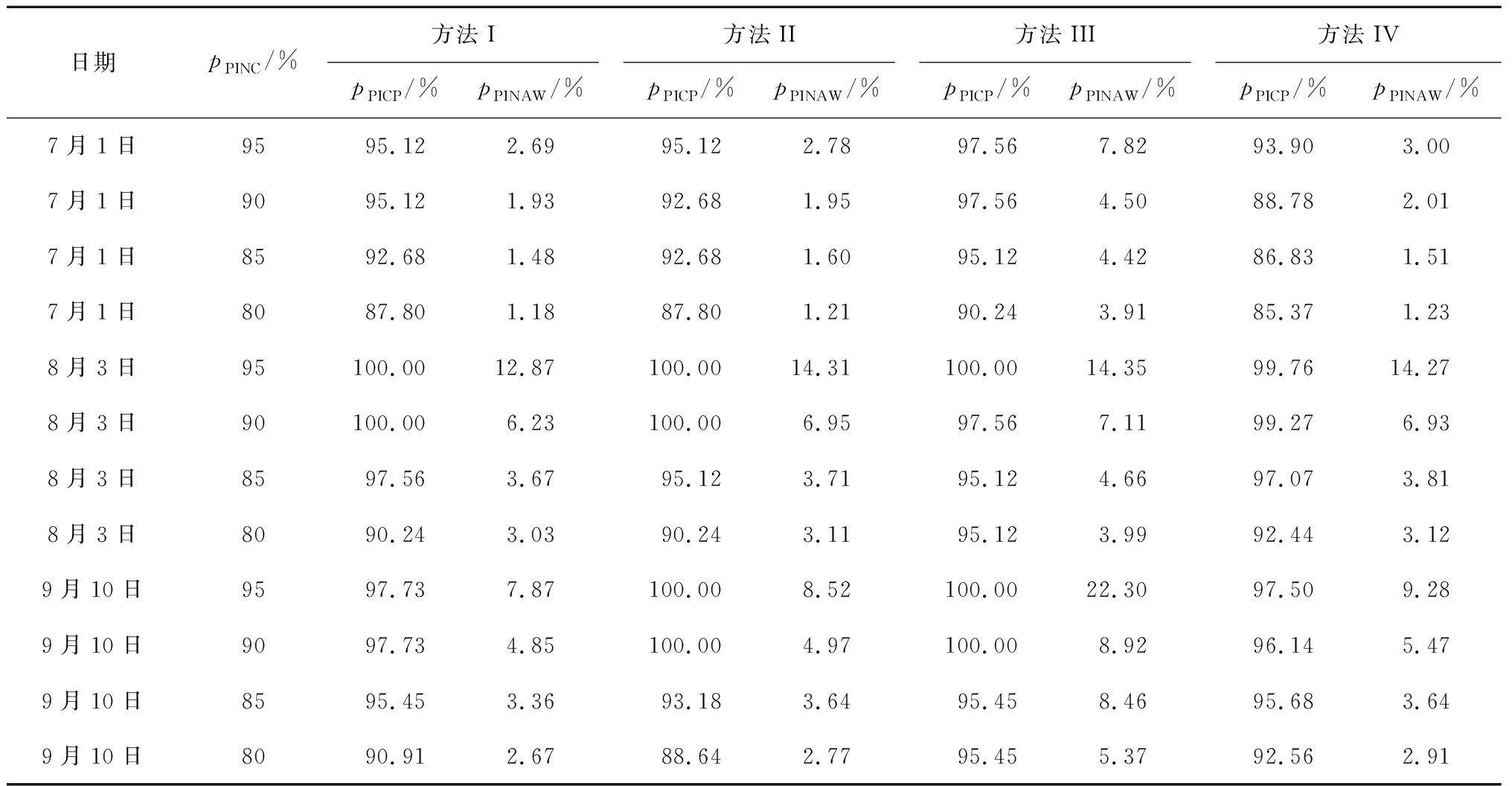
表4 不同方法区间预测结果对比Tab.4 Comparison of interval prediction results obtained from different methods

方法I和方法II在各种情况下的对比结果显示,两种方法得到的预测区间PICP较为接近,但加权欧氏距离指标与普通欧氏距离指标相比,采用前者选择出的ELM训练集可获得更窄的PINAW,即可有效提高光伏功率区间预测的准确度.这是因为权重的设置充分考虑不同气象因素与光伏功率之间的相关性大小,选择出的ELM训练集与待预测样本相似程度更高.

从方法I和方法 III 的对比可得出,两者的PICP均能满足置信水平要求,某些情况下方法III结果的PICP甚至略优于方法I.但从准确度角度来看,方法 I 结果的PINAW在不同情况下均明显小于方法 III.此对比结果说明,ELM训练集筛选可以大大提高预测准确度.

从表4数据中可以看出,在可信度与准确度两方面,方法 I 得到的预测区间评估指标在各个情况下均优于方法 IV 结果相应指标的期望值,说明ELM隐藏层输入权重与偏置的寻优可以降低随机生成参数给预测结果带来的不稳定性,有效提高预测区间的可信度与准确度.