溯本清源 格物致知

文／武妍

例1【苏科版数学教材七（下）80页第2题】用不同的代数式表示图1中草坪的面积。由此，你能得到怎样的等式？试用整式乘法法则说明这个等式成立。

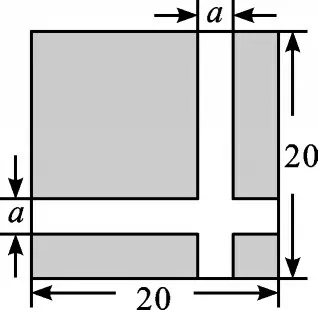
图1

【解析】观察图形可知，草坪的面积等于大正方形的面积减去两条路的面积，但要注意有重叠部分。故可得S=20×20-2a×20+a·a=400-40a+a2。

将图中的两条路平移至两边后，可得草坪的面积为S=（20-a）2。

利用完全平方公式对（20-a）2展开，可得400-40a+a2。

∴等式（20-a）2=400-40a+a2成立。

【点评】本题考查了完全平方公式的几何背景。观察得出等式并明确完全平方公式是解题的关键。

变式如图2，两个正方形边长分别为a、b，且满足a+b=10，ab=12，则图中阴影部分的面积为________。

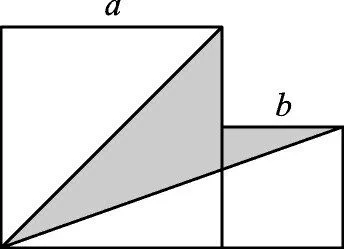
图2

【解析】将a+b=10两边平方，得

在课前准备阶段，利用虚拟共享实训平台发布变速箱拆装实训的相关演示动画和讲解视频，使学生提前对拆装对象有更加直观的了解，同时通过演示动画和讲解视频熟悉拆装的操作规范和注意事项，做到有目的、有效果的课前准备。

将ab=12 代入，得a2+b2+24=100，即a2+b2=76，

则两个正方形面积之和为76。

【点评】我们还可将图中阴影部分切割成两个三角形，分别表示出两个三角形的面积再求和。本题充分体现了割补法求面积的巧妙之处。

例2【苏科版数学教材七（下）90页第10题】

观察下列式子：

探索以上式子的规律，试写出第n个等式，并说明第n个等式成立。

【解析】两个连续偶数的积与1 的和等于这两个偶数中间的奇数的平方，即2n（2n+2）+1=（2n+1）2（n为正整数），左边=4n2+4n+1=右边，所以等式成立。

【点评】本题考查数字的变化规律，通过观察所给的式子，利用整式运算即可求解。

变式观察下列算式：

①1×5+4=32，②2×6+4=42，③3×7+4=52，④4×8+4=62，……

请你观察规律解决下列问题：

（1）填空：____×_____+4=20152。

（2）写出第n个式子（用含n的式子表示）并证明。

【解析】（1）由以上4个等式可以看出规律：每一个等式中第一个数字等于序号数，第二个数字比第一个大4，等式右边的底数比第一个数大2，指数始终为2。因此，2013×2017+4=20152。

（2）由（1）可知第n个等式为n（n+4）+4=（n+2）2。

∵左边=n2+4n+4=（n+2）2=右边，

∴n（n+4）+4=（n+2）2成立。

【点评】本题是教材原题的翻版，大部分同学可迅速发现规律并证明，证明时可分别求解左右两边，证明等号左右两边相等即可。