废弃矿井巷道围岩蠕变稳定性分析*

2024-03-26胡昌顺杨彦群

现代矿业 2024年1期

胡昌顺李宁杨彦群

（1.安徽理工大学土木建筑学院；2.安徽理工大学矿业工程学院；3.山西焦煤集团有限责任公司）

蠕变特性是岩体的重要力学性质之一，其长期强度与工程的稳定性密切相关。随着我国煤矿不断向深部开采，高应力、高温及高水压力使得开采环境劣化，煤岩体的稳定性进一步降低。近年来，随着我国煤炭行业供给侧改革的不断推进，中西部地区废弃矿井数量增加，导致大量的地下空间资源没有得到充分利用。对遗留地下空间进行储水、储油等方式，面临的最大威胁就是深部复杂地质条件下的煤岩体长期蠕变破坏现象。

近年来国内很多专家对深部巷道围岩稳定性问题进行了深入研究，并提出了行之有效的支护设计方案。经来旺等［1］通过对软岩巷道围岩质点应力状态进行分析，得到了“强表抑蠕”新原理，并提出双层网壳锚喷高强支护技术；王卫军等［2］提出“可接长锚杆+刚性长螺纹钢锚杆+锚网+W 钢带+喷射混凝土”的支护方案；贾晓亮［3］分析了巷道底鼓原理，提出“构筑反底拱+底板注浆+底板锚杆”联合支护方案；丁增等［4］通过蠕变试验与数值分析，得到深部巷道蠕变机理；崔巍等［5］提出了“锚索+锚杆+喷射混凝土+注浆”联合支护方案；吴标等［6］通过分析原支护情况下巷道变形及破坏机理，提出锚杆锚索+二次锚注耦合支护方案；谭文兵等［7］对巷道采用不同支护方式进行模拟，得到优化锚网喷支护方案。然而考虑不同支护结构下的深部高地应力巷道蠕变作用数值模拟研究则较少。对于废弃矿井地下空间利用，特别是储水、储油及储气等利用方式，需要围岩在长时间的服务期内保证稳定，因此对废弃矿井大巷进行蠕变下的变形分析及支护模拟尤为关键。通过研究深部巷道围岩蠕变破坏的机理和规律，进而采取合理的支护措施保证巷道空间的稳定安全，最终建立可靠的地下空间再利用方案。

本文以某废弃矿井深部-650 m 的水平巷道为背景，通过数值模拟分析锚杆+预应力锚索+衬砌组合、锚杆+预应力锚索+钢拱架组合和衬砌3 种支护环境下的围岩受力和支护结构协同变形过程，对深部巷道围岩蠕变效应下支护稳定性进行研究，为废弃矿井地下空间安全利用提供理论依据。

1 数值模拟过程

1.1 巷道蠕变破坏分析

对于废弃矿井大巷储水等利用形式，巷道破坏的因素应主要考虑岩体的长期强度和安全强度。岩石的蠕变曲线如图1所示，如果围岩应力值低于安全强度，则不会发生蠕变，如曲线b所示；若在接近长期强度的较高应力值下，则发生不稳定蠕变，变形发展迅速直至破坏，如曲线c 所示；当应力值在安全强度和长期强度之间时，如曲线a 所示，则首先发生OA段围岩的短期变形响应，包括弹性和塑性变形。然后产生AB和BC2 个区段的衰减和稳态蠕变［8-10］。因此，对于废弃矿井大巷来说，通过不同的支护组合设计使得围岩处于曲线b 及曲线a 的前2 个阶段，则能够很好地对围岩蠕变进行控制，保证地下空间长期利用的安全和稳定。

1.2 数值模拟模型与参数确定

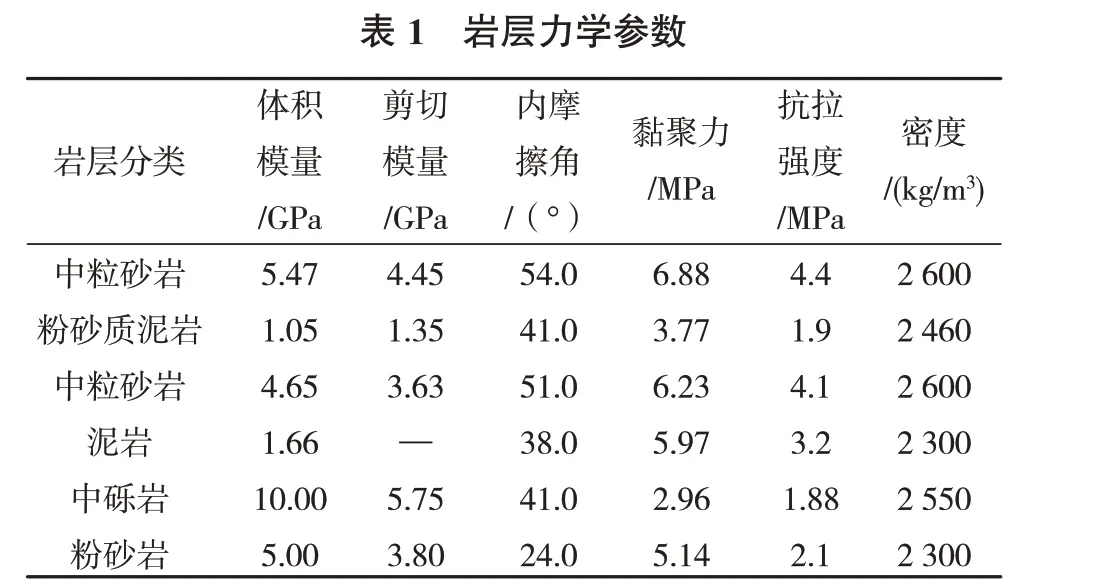
根据现场的钻孔综合柱状图，得到巷道周边岩层的力学参数如表1所示。最终建立如下数值模型：尺寸为30 m×10 m×29 m，共划分了69 600 个单元格，由上至下模型分为6层，各层厚度由上至下依次为4，3，3，8，1.5，9.5 m。

依据工程实际环境，巷道及其所在岩层为泥岩，其能够体现较强的蠕变特性，故采用Burgers-Mohr本构模型研究巷道所在岩层的围岩蠕变变形破坏机理，其中Kelvin 体弹性模量及Maxwell 体弹性模量分别取2.5 GPa 和1.6 GPa，黏性系数分别取730 GPa·h和220 GPa·h。其余各岩层性质因蠕变效应不明显，故采用摩尔-库伦本构模型进行模拟。

1.3 支护方案确定

本计算模型中支护结构采用FLAC3D内置liner、cable 及beam 单元。锚杆+预应力锚索+衬砌支护方案布置方式：顶板以及左右两帮中部沿纵深布置排间距为1 m、长度4 m 的锚杆，巷道左右帮部与半圆拱交界处沿纵深布置排间距1 m、长度10 m、预应力为90 kN 的锚索，巷道表面采用衬砌支护。锚杆+预应力锚索+钢拱架支护方案布置方式：沿纵深布置排间距1m 的钢拱架，并在顶板和左右帮中部沿纵深布置间距1 m、长度4 m 的锚杆，帮部四角处沿纵深布置排间距1 m、长度10 m、预应力为90 kN的锚索。衬砌支护方案布置方式：巷道表面采用衬砌支护。

2 模拟结果分析

2.1 围岩变形分析

选取2 a时间窗进行分析，对拱顶、左帮中点及左部交界处进行位移和应力监测，得到2 a 后巷道蠕变变形情况、3 种支护条件下的水平及竖直方向位移云图（图2、图3），进而反映出长期蠕变后围岩的受力情况。

从图2 可知，巷道水平位移云图左右对称，在衬砌支护方案下，帮部与交界处蠕变量为30～40 cm，水平位移在帮部表面对称扩散。在锚杆+预应力锚索+衬砌支护条件下，帮部与交界处蠕变量为5～10 cm，两帮部围岩位移变形分布呈弧形对称特点。在锚杆+预应力锚索+钢拱架支护条件下，位移量过大，说明巷道已完全失稳破坏，故不做分析。

从图3 可知，在2 a 蠕变过程中存在巷道拱顶下沉和底鼓的现象。在衬砌支护方案下，拱部蠕变量为15～17.9 cm。在锚杆+预应力锚索+衬砌支护方案下，拱部蠕变量为2～3 cm。相比之下，锚杆+预应力锚索+衬砌支护的支护效果更好，顶底板整体的位移量相对衬砌支护较小，巷道表面位移量较为均匀。

综上所述，3种支护方案在2 a时间窗的蠕变作用下，围岩变形的控制效果对比鲜明。作为纯刚性的衬砌支护未能很好地控制变形，而锚杆+预应力锚索+钢拱架支护虽有锚杆和锚索材料的加强支护，但仍未达到理想效果。锚杆+预应力锚索+衬砌支护能够很好地控制围岩的变形，实现地下空间的长期利用。

2.2 围岩应力动态分析

虽然在废弃矿井地下空间利用过程中，由采动引起的大范围应力重分布不再发生，但是蠕变过程引起的围岩小范围移动及造成的应力重分布依然存在。围岩的应力水平决定了蠕变的速率及巷道是否会发生失稳。因此，本模拟得到了蠕变2 a 后的垂直和水平方向应力云图（图4、图5）。

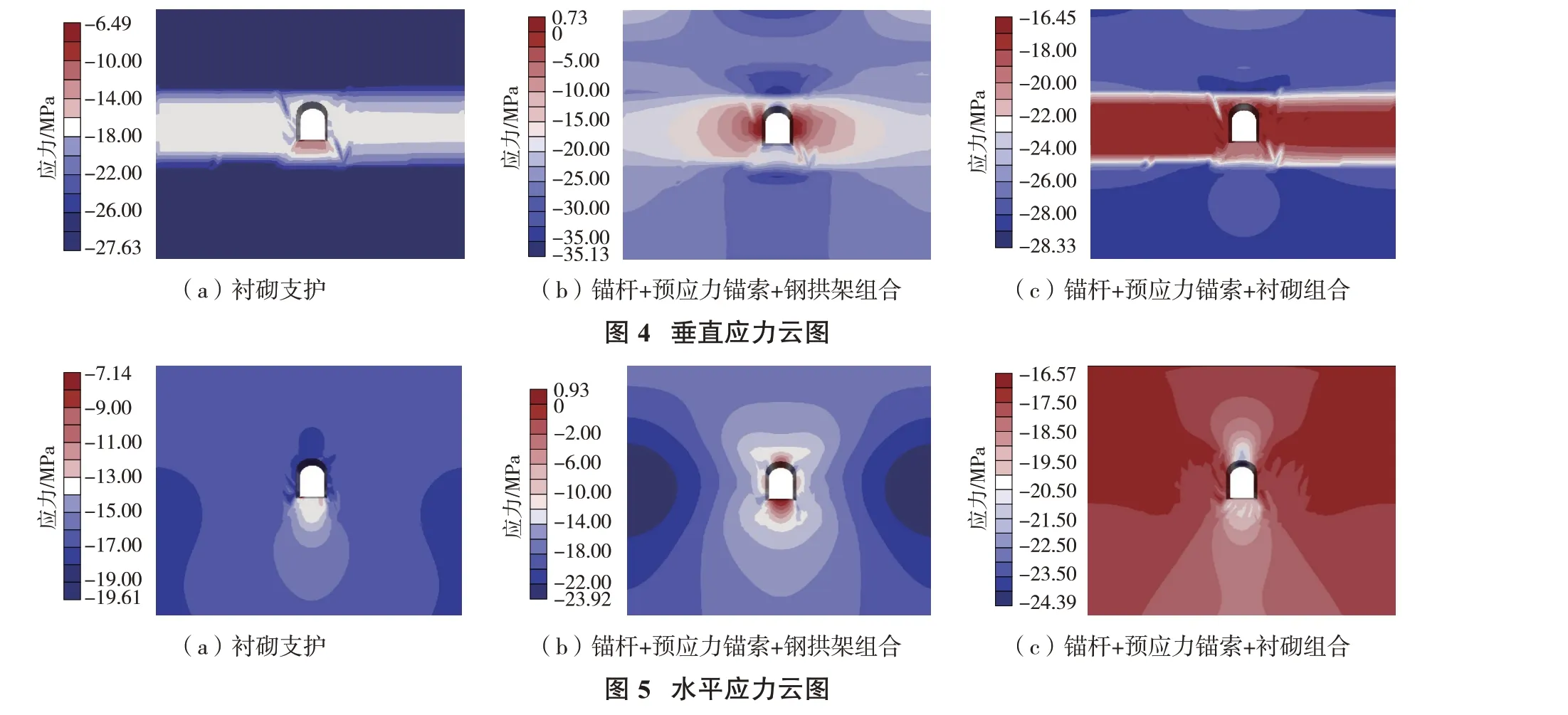
从图4 可知，随着蠕变的开始，巷道变形量出现了明显的增大，应力也得以释放，各支护方式下的应力分布都有不同程度的变化。衬砌支护方案在巷道拱部表面存在较高应力集中现象；锚杆+预应力锚索+衬砌支护方案在巷道附近应力分布较均匀，蠕变期间巷道围岩应力均为压应力且状态稳定；锚杆+预应力锚索+钢拱架支护在巷道围岩表面存在部分拉应力，极易产生拉破坏。此结果也验证了钢拱架支护方案产生过大变形而破坏的情况。

从图5可知，支护结构使得巷道所处岩层范围内水平应力更加均匀。但锚杆+预应力锚索+钢拱架支护的应力状态并不稳定，与垂直应力一样出现一定范围拉应力，进而造成了较大的位移。

综上所述，蠕变过程中浅部围岩首先破坏，然后集中应力向深部围岩转移。从衬砌支护的应力分布可以看出，单一的支护材料并不能充分抑制蠕变，锚杆+预应力锚索+钢拱架支护在左右帮部也未能有效控制应力状态。而锚杆+预应力锚索+衬砌支护则削弱了应力集中现象，改变了支护体的力学性质，有效控制了围岩的大变形。

2.3 围岩蠕变过程分析

3 种支护方式的顶板点、交界点、左帮点的位移、应力、最大主应力与最小主应力的差值情况如图6～图8 所示。从图6、图7 可以看出，衬砌支护与锚杆+预应力锚索+衬砌支护位移曲线变化趋势为先增大后趋于平稳，蠕变速度也趋于平缓，与其监测的应力曲线相对应，其中锚杆+预应力锚索+衬砌支护最为平稳。锚杆+预应力锚索+钢拱架支护由于支护强度的不足以及长期蠕变影响，岩层逐渐由弹性转变为塑性，最终导致巷道失稳。从图8 可以看出，巷道蠕变动力取决于最大主应力与最小主应力差值（σ1-σ3）的变化，随着蠕变时间的增加，锚杆+预应力锚索+衬砌支护最大主应力与最小主应力差值在部分监测点已为零，衬砌支护的最大主应力与最小主应力差值虽不为零，但差值非常小，保持在长期强度与安全强度之间，巷道发生可控的稳定蠕变。锚杆+预应力锚索+钢拱架支护中σ1数值剧增，σ3数值降低至很小数值，导致围岩一定范围内的（σ1-σ3）变得很大，超过其长期强度值，蠕变过程可能以加速方式直至破坏状态，且荷载越大其失稳过程越快。