对平行线中“拐点”问题的探索与思考

文／江苏省太仓市沙溪镇岳王学校 刘夏天

在学习平行线相关性质时，我发现有一类题目经常出现。在平行线之间或者外部添加一个“拐点”，将这个点与两条平行线上的点连接，会出现很多角，这些角区别于我们所学的同位角、内错角与同旁内角，但它们之间又有一定的潜在关系。因此，我想将这些关系整理下来，与大家分享。

类型1 已知，如图1，AB//ED，求∠ABC、∠BCD、∠CDE三个角之间的数量关系。

图1

该类型与上一篇文章《平行线中的魔法》的问题1 是一样的。拐点C在两条平行线之间，我们可以过点C，构造AB、ED的平行线CF，如图2，使∠BCD分成∠BCF与∠FCD，随后可以发现∠BCF、∠FCD分别与∠ABC、∠CDE是内错角的关系，利用平行线的性质，可以得到∠BCD=∠BCF+∠FCD=∠ABC+∠CDE。

图2

类型2 已知，如图3，AB//ED，求∠ABC、∠BCD、∠CDE三个角之间的数量关系。

图3

该类型中，拐点C也在两条平行线之间，但点B、C、D之间的位置关系与类型1 稍微有些不同，我们仍然可以用类型1的方法，过点C构造平行线FC，如图4，但此时∠BCF、∠FCD分别与∠ABC、∠CDE是同旁内角的关系，可以得到∠BCF+ ∠ABC=180°，∠FCD+ ∠CDE=180°。因 此，∠ABC+ ∠BCD+ ∠CDE=∠ABC+∠BCF+∠FCD+∠CDE=180°+180°=360°。

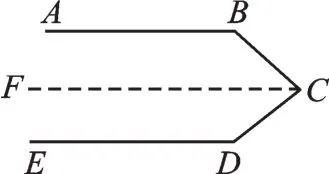
图4

类型3 已知，如图5，AB//ED，求∠ABC、∠BCD、∠CDE三个角之间的数量关系。

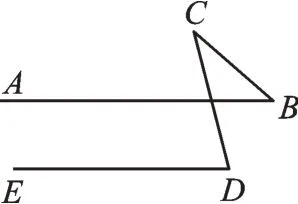
图5

该类型中，拐点C在两条平行线之外，当然，我们也可以用类型1 与类型2的方法，作平行线来解决，但我认为有更简单的方法。此图形中有一个现成的三角形，不妨设AB与CD的交点为点F，利用平行线的性质，可得∠CDE=∠CFA，而∠CFA又 是△CFB的 外 角，可 以 得 到∠CFA= ∠ABC+ ∠BCD，因 此，∠CDE=∠ABC+∠BCD。

以上三个类型的基本题型，就是我通过对平行线中“拐点”问题的探索与思考后，整理出来的。经过这番整理与总结，我感觉自己对这类题目有了更深的理解。

教 师 点 评

在学习几何的过程中，对问题进行总结与提炼，并归纳成基本题型，是对大家抽象思维和概括能力的锻炼，也能让大家在做题时有更灵活的思维。期待同学们能够在练习的过程中发现更多的基本图形，并能够自我创新，对基本题型进行改编，进一步提升数学素养。