基于COMSOL 的剪切速率对超声波流量测量影响分析

2024-03-25刘升虎王建志

石油化工应用 2024年2期

刘升虎，魏一，王建志

（1.西安石油大学陕西省油气井测控技术重点实验室，陕西西安 710065；2.中国石油天然气股份有限公司华北油田分公司第三采油厂，河北沧州 062450）

随着全球能源需求增长和老油田开发进入中后期产量减少的矛盾越来越突现，EOR（提高采收率）技术已经成为老油田提高可采储量的主要技术[1]。聚合物驱油是提高石油采收率最常用的方法。早在20 世纪末，我国利用聚合物驱的采油量就位居世界第一。注聚效果往往是决定油田产量的主导因素[2]。聚合物的流量影响着驱替效果，流速过快，会导致聚合物溶液在高渗透率渗流速度过快；对于油田现场，若提高注入速度，则有可能导致过高的注入压力，因此，对注聚流量进行测量至关重要[3]。但国内外对于注聚流量的研究较少，尤其是超声波测注聚流量，哪些因素会对超声波测注聚流量的效率和结果造成影响是目前学者需要关注的问题，不能忽略的因素要对结果进行相应的优化和补偿，提高测量结果的准确性。本文探讨的是聚合物剪切速率的不同对于流体流态和超声波测量的影响，分析仿真结果为后续其他影响因素的研究打下基础。

1 超声波流量测量原理

全球超声波流量计主要应用领域分别为水、废水、石油天然气、化学品、能源行业、造纸行业和食品与饮料行业等[4]。从全球所有行业的超声波流量计使用情况来看，化学品、石油天然气和能源行业是超声波流量计的主要消费领域，占到全部使用量的一半[5]，在石油行业中其多用于测量井下注水与油水两相的流量。超声波时差法的实现原理是分别测量超声波在流体中顺流传播时间和逆流传播时间，并将顺流传播时间与逆流传播时间做差从而获得传播时间差，根据传播时间差与被测流体流速、流量之间的关系来实现流量测量[6]。其本质是超声波在流体中传播时，传播速度受到流体流速的影响，通过计算顺流和逆流的传播时间差再代入公式得到流体的瞬时流速，最后计算流量。超声波流量计的核心传感器是换能器，是一种能将电信号转换为声信号或者将声信号转换成电信号的装置[7-8]。具体操作见图1，将A、B 两个超声换能器按照“Z”字排列在管道外侧，测量顺流和逆流时超声波在流体中的传播时间。

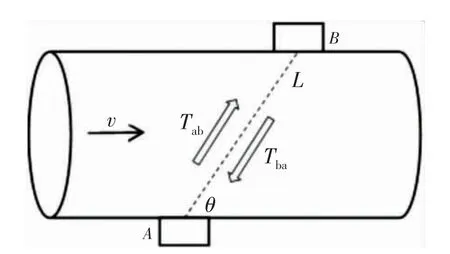
图1 超声波流量测量原理图

顺流飞行时：

逆流飞行时：

式中：c-超声波在介质中的声速，m/s；v-流体流速，m/s；θ-飞行距离与流体流向间的夹角，°；L-飞行距离，m；Tab-顺流飞行时间，s；Tba-逆流飞行时间，s。

根据两式可以推导出流体流速：

从而计算出瞬时流量：

式中：Q-流量，m3/s；S-管道横截面积，V。

2 剪切速率

利用剪切应力和剪切速率的关系可将流体划分为牛顿流体和非牛顿流体，剪切应力和剪切速率之间关系是线性为牛顿流体，非线性为非牛顿流体。根据非牛顿流体黏度受外力改变的特性，可大致将其分为三类：非时变性流体、时变性流体和黏弹性流体[9]。幂律模型是在研究非牛顿流体时常用的基本经验模型。

幂律流体本构方程为：

式中：μa-表观黏度，Pa·s；K-稠度系数，Pa·sn；n-流变指数；γ-剪切速率，s-1。

表观黏度是剪切速率的函数，n=1 时，剪切应力和剪切速率呈线性关系，符合牛顿内摩擦定律，为牛顿流体；n＞1 时，K 随剪切速率的增大而增大，为剪切变稠流体；n＜1 时，K 随剪切速率的增大而减小，为剪切变稀流体[10]。流变测试表明，聚合物溶液有剪切变稀的特性，表观黏度μa随剪切速率γ 的变化符合幂律模型[11]。

3 基于COMSOL Multiphysics 仿真分析

3.1 超声波流量测量模型构建

本文采用COMSOL Multiphysics 6.1 模型搭建和仿真，使用的模型为时差法超声波流量计在测量过程中常用的外夹式，通过仿真来分析聚合物不同剪切速率对流体流态和超声波传播的影响。为了提高计算效率方便结果对比，只显示一半管道，管道管径为50 mm，长度为300 mm，换能器与管道的夹角为45°，模型两端设置吸收层用于截断计算域，超声波流量测量模型见图2。

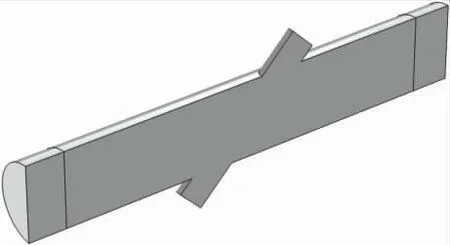
图2 超声波流量测量模型

在声学部分的网格构建过程中网格划分需要手动设置，在利用“对流波动方程，时域显式”模型求解时内部时间步进大小由CFL 条件严格控制，在设置自由四面体网格单元时要控制最大单元和最小单元的大小，将其设置为1/2 波长和2/3 波长之间的任意值，以此来获得一些空间分辨率。研究背景流时的网格划分和研究声学时的网格划分见图3。

图3 不同研究的网格划分

3.2 不同剪切速率下的流体流态分析

油田中注入的聚合物为聚丙烯酰胺颗粒与水溶液搅拌混合后的溶液属于单相流，而单相流仅有层流和紊流两种形态，因此，在物理场设置中选择“层流”，右侧为流体入口，左侧为流体出口，平均流速为10 m/s。因为在COMSOL 材料库中没有聚合物，所以管道中的聚合物流体需自行设置，在流体属性中本构关系选择非弹性非牛顿，非弹性模型选择幂律，参数设置根据聚合物本身的性质进行添加。聚合物黏度较大在流速很大的情况下也呈现为层流状态，图4 和图5 分别为聚合物在剪切速率为1、200 s-1的背景流速幅值和聚合物在剪切速率为1、50、100、200 s-1的背景流速曲线。

图4 不同剪切速率背景流速幅值

图5 不同剪切速率背景流速曲线

通过对比剪切速率分别为1、200 s-1的背景流速幅值和1、50、100、200 s-1的背景流速曲线可知，在其他数据不变的情况下，改变聚合物的剪切速率，其流体流态会逐渐发生变化，且剪切速率越大流体流态越趋向于湍流。

3.3 不同剪切速率下超声波接收声压大小分析

超声波部分用COMSOL 中“对流波动方程，时域显式”物理场来模拟超声波的传播，将流体模型的解应用到超声波部分需要添加背景流体流动耦合多物理场和映射研究，设置管道上侧的换能器为发射器，管道下侧的超声换能器为接收器，超声换能器的超声波发射频率为2.5 MHz，在管道两端设置声阻抗来截断计算，图6 是在7E-6 时刻的声速、声压、声强和超声波发射器及接收器的声压波形（剪切速率为1 s-1），需要对比不同剪切速率下的接收器声压最大值，进而得出剪切速率与接收器声压之间的关系。

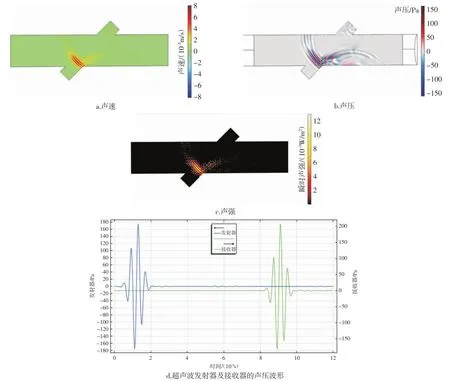
图6 在7E-6 时刻的声速、声压、声强和声压波形（剪切速率为1 s-1）

仿真实验选择的剪切速率分别为1、10、20、50、100、150、200 s-1，温度为20 ℃时，对应的接收器声压最大值分别为208.38、209.94、210.35、210.68、210.80、210.83、210.85 Pa。聚丙烯酰胺水溶液的剪切速率与超声波接收器声压最大值关系见图7。

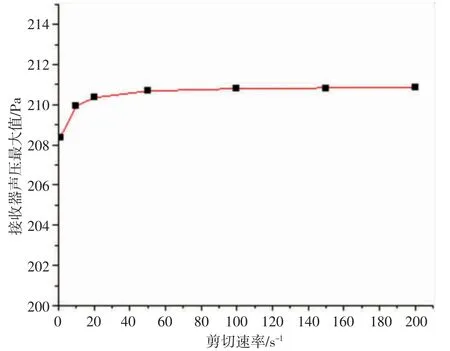
图7 聚丙烯酰胺水溶液剪切速率与超声波接收器声压最大值关系图像

由图7 可知，相同温度条件下溶液剪切速率和接收器声压最大值不是线性关系，剪切速率在1～50 s-1变化时对接收器声压最大值影响较大，在剪切速率超过50 s-1后对于接收器声压最大值的影响逐渐减小，图像趋于水平，测量数据的最大值与最小值相差1%，差距过小且各数据间没有明显的规律可循，因此，聚丙烯酰胺水溶液剪切速率对于超声波接收器声压最大值的影响可以忽略。