Recent advances in protein conformation sampling by combining machine learning with molecular simulation

Yiming Tang(唐一鸣), Zhongyuan Yang(杨中元), Yifei Yao(姚逸飞), Yun Zhou(周运), Yuan Tan(谈圆),Zichao Wang(王子超), Tong Pan(潘瞳), Rui Xiong(熊瑞), Junli Sun(孙俊力), and Guanghong Wei(韦广红)

Department of Physics,State Key Laboratory of Surface Physics,and Key Laboratory for Computational Physical Sciences(Ministry of Education),Shanghai 200438,China

Keywords: machine learning,molecular simulation,protein conformational space,enhanced sampling

1.Introduction

Proteins, the fundamental building blocks of life, are involved in every cellular process,driving a vast range of functions, and are also central to the mechanisms of various human diseases.The structural complexity of proteins, dictated by their amino acid sequences, is fundamental to their multifunctional roles across biological processes.[1,2]Protein misfolding or even minor alterations in protein sequence can profoundly disrupt cellular activities, leading to diseases such as Alzheimers,Parkinsons,and cancer.[3,4]Thus,the exploration of protein conformational ensembles stands as a cornerstone in biomedical research,pharmaceutical advancements,and an indepth and comprehensive understanding of life at the molecular level.Despite the remarkable power of experimental protein structure determination techniques such as NMR spectroscopy,x-ray crystallography,and cryo-electron microscopy(cryo-EM),[5-7]a substantial portion of protein structures remains unsolved.Furthermore, the recent discovery of intrinsically disordered proteins (IDPs) as important physiological and pathological function carriers poses a challenge.[8-11]Their structural diversity and dynamic conformational landscapes make experimental characterization of IDPs’ conformational ensembles a mostly unresolved task.

Theoretical and computational methodologies have emerged as indispensable tools in exploring the conformational properties of proteins,particularly the dynamic conformational ensembles of IDPs.[12-16]In a groundbreaking proofof-principle study a decade ago,[17]Shawet al.presented atomic-level microsecond molecular dynamics (MD) simulations showing how 12 fast-folding proteins fold to their native structures.Over the past decades, extensive computational studies have been conducted on proteins with more complex conformational landscapes.[18-20]These studies have been advanced by methodological and technical developments such as GPU-accelerated MD algorithms,[21,22]specially designed force fields,[18,23,24]and enhanced sampling methods including temperature replica exchange,[25]accelerated MD,[26,27]and metadynamics simulations.[28,29]Despite these achievements, computational studies continue to face challenges in efficiently sampling the vast conformational space of proteins,particularly IDPs.Consequently,there is an urgent demand to pioneer new strategies that expedite the computational exploration of protein conformational landscapes.

In recent years, machine learning methods, particularly neural networks, have been successfully applied in computational molecular science,[30-33]such as predicting protein-ligand[34]and protein-protein interactions.[35,36]AlphaFold,[37]introduced in 2018 and significantly improved by 2020,has made groundbreaking advancements in the field of protein structure prediction,[38,39]a challenge that has stumped scientists for decades.This breakthrough proves the capability of machine learning in solving complex scientific problems.Hybrid methods that combine MD simulations with machine learning have demonstrated the potential to achieve enhanced sampling of the conformational landscape with higher efficiency.[40,41]Such advancements underscore the synergy between computational biophysics and machine learning, and pave the way for an in-depth understanding of protein folding,conformational landscapes,and functions.

In this review, we delve into recent progress in machine learning-based strategies that synergize molecular simulations with machine learning to enhance the exploration of protein conformational landscapes.These strategies broadly fall into three categories.The first encompasses methods where machine learning refines the selection of reaction coordinates or the most promising sampling direction.The second category of techniques utilizes autoencoder based neural networks to generate samples from the unexplored region of prior simulations.The third category of methodologies trains invertible encoders by a combination of MD samples and energy functions to generate Boltzmann weighted conformations.The advantages and limitations of these methods are also discussed.

2.Heuristic and machine learning algorithms for the enhanced exploration of the conformational landscape

Computational simulations stand as a preeminent and powerful tool for revealing the molecular mechanism of protein structural transformations by exploring the energy landscapes.However,for structured proteins,challenges rise when their energy landscapes comprise metastable states separated by high barriers that confine the simulation within the restricted terrain of the landscape.[42,43]For IDPs, the situation is further complicated by an exponentially increasing number of metastable states,which drastically magnifies the complexity of the energy landscape and the demand for computational resources.[44,45]To expedite the exploration of proteins’ conformational space, a number of enhanced sampling methods have emerged which fall into several categories as reviewed in Refs.[46,47].A pivotal group of enhanced sampling techniques, including umbrella sampling,[48]steered molecular dynamics (SMD),[49]and metadynamics,[50]bias the molecular potential along one or more collective variables (CV)to facilitate the exploration along slow coordinates.However,they rely on the appropriate selection of pre-defined CVs that should accurately embody the physical processes being studied.[51-53]

A number of efforts have been made to develop machine learning based methodologies to determine the optimal choice of CVs without prior knowledge of the system.[54-56]These methods require a short trajectory from an unbiased MD simulation.Neural networks are trained based on the MD trajectory to transform protein conformations into dimension-reduced latent coordinates as CV candidates (Fig.1(a)).As one of the pioneer works, Pandeet al.developed a variational autoencoder(VAE)which comprises two hidden DenseNet layers for the encoder and two layers for the decoder (Fig.1(b)), and trained the network based on a 170-ns-long all-atom simulation on the alanine dipeptide.[57]The VAE transformed the conformational space of alanine dipeptide, described using two dihedrals (Ψ,Φ), into a one-dimensional latent space.The latent coordinate was able to separate all three major conformations of the dipeptide.For the 35-residue FIP WW domain, it was necessary to first perform a time-structure based independent component analysis(tICA)[58,59]to reduce the extensive conformational space into a more manageable two-dimensional independent component (IC) space.Subsequently, the VAE network further transformed the IC space into a single-dimensional latent space.The latent coordinate was then adopted as the CV for well-tempered metadynamics simulations that simultaneously sampled folded,unfolded,and misfolded states.Although the network architecture employed is relatively straightforward and remains untested on larger proteins,this research stands as a pioneering effort,offering a valuable opportunity to engineer network architectures for the latent reduction of protein conformational spaces and the optimization of CV selection for enhanced sampling techniques.

By substituting the DenseNet architecture within the VDE network with more sophisticated and advanced architectures, more complicated systems can be investigated.The LINES method[60]employed a state-of-the-art flow-based machine learning model (Fig.1(c)) to learn a dimensionpreserving transformation from conformational space to latent space.When combined with molecular potential,a welltrained normalizing flow can identify reaction coordinates associated with the slow degree of freedom in the system.By establishing a bias potential via a tabulated grid decomposition of the reaction coordinate values and performing biased MD simulations,Liuet al.simulated the unbinding of cyclobutanol fromβ-cyclodextrin and obtained a more precise prediction of binding affinity compared to conventional MD.The LINES method had also been applied to the selection of CV for simulating the unfolding and refolding processes of CLN025, a Chignolin variant.Later, the same group utilized the LINES approach to study the binding of Galectin 9 with the 109-residue lgV domain of an immune regulation receptor protein,TIM3.Their simulations,boosted by LINES-derived bias potential, accurately identified the binding site and revealed the physical interactions underlying the binding process.[61]However, LINES can only predict a one-dimensional reaction coordinate, thus limiting its application to proteins whose conformational change consists of a series of intermediate conformations.

One of the shortcomings of the machine-learning-based bias potential is the absence of physical interpretations for the latent parameters.To address this limitation, Tiwaryet al.developed an iterative scheme that combines the deep learning framework of VAE with physical intuitions.[62]This method was named the reweighted autoencoded variational Bayes for enhanced sampling(RAVE).After generating the latent interpretation of the conformational space through VAE,it screened through various linear combinations of input order parameters that were user-built from experimental data and/or chemical intuition,so as to determine a CV whose MDsampled distribution was closest to the distribution of the latent coordinate (Fig.1(d)).The usefulness and reliability of RAVE were demonstrated by applying it to two model potentials (the Szabo-Berezhkovskii potential and a three-state potential) and a hydrophobic buckyball-substrate system in explicit water.It is noted that the applicability of RAVE on biomolecules such as proteins has not yet been explored.

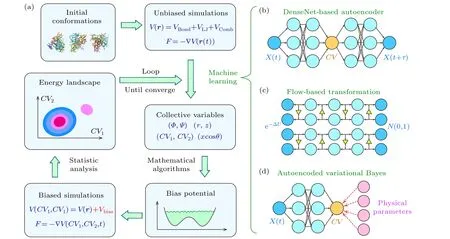
Fig.1.Schematic diagram showing the machine-learning aided optimization process of collective variables.(a)The workflow diagram depicting the integration of machine learning for collective variable optimization within enhanced sampling simulations.(b)-(d)Schematic of the neural network architectures designed for learning the optimized collective variables from simulation data.

These outlined works have provided useful methodologies for optimizing the selection of collective variables(CVs),thereby enhancing the exploration efficiency in model potentials and simple systems.However, these methods[57,60-62]have limitations in terms of the number of latent coordinates(usually equivalent to the number of CVs) that the networks are designed to encode.The few number of CVs may limit the application of these methods on large proteins with complex conformational landscapes.

One of the primary obstacles preventing simulations from effectively sampling the entire conformational landscape is the frequent entrapment in local minima, which results in the excessive simulation time consumed in already sampled regions.[63,64]Various heuristic and machine learning algorithms have been developed to prioritize and enhance the exploration of less-sampled regions.Methods like structural dissimilarity sampling (SDS),[65]self-avoiding conformational sampling (SACS),[66]and complementary coordinates MD(CoCo-MD),[67]reduce the dimension of the energy landscape of sampled conformations by principal component analysis (PCA), and select seed structures from the dimensionalreduced landscape.Adaptive sampling methods, such as parallel cascade selection MD (PaCS-MD),[68]employ Markov state models to cluster all sampled conformations into microstates and then restart parallel simulations from those microstates.Shuklaet al.developed the reinforcement learning based adaptive sampling(REAP)algorithm[69]which enables an on-the-fly estimation of the relative importance of a predefined set of CVs.The REAP-based simulations include three iterative steps: (i) run a series of short MD simulations, (ii) cluster the protein conformations in the predefined CV space,and(iii)pick seed structures from these clusters based on a reward function measuring the relative importance of each order parameter(Fig.2(a)).The REAP methods are applied to explore the energy surface of alanine dipeptide and the 42-residue Src Kinase.However, the functionality of REAP is limited by its underlying assumption that new regions of the landscape will tend to show new extrema along the prioritized CVs, thus its performance is poor when sampling systems characterized by energy landscapes with minimal symmetry.[70]This limitation has been mitigated by incorporating multiagent reinforcement learning(MARL)which learns simultaneously from different regions of the energy landscape through coordinated agents.[70]

Fig.2.Flowcharts of two different machine-learning aided enhanced sampling methods.(a)The workflow diagram of the REAP methods.(b)The workflow diagram of training a machine-learning based coarse-grained potential for enhanced sampling.

Later, a similar, but CV-free approach was employed by Zhang and Gong, named frontier expansion sampling(FEXS).[71]After each MD cycle,the authors performed PCA on all sampled structures,decomposed all conformations into a number of sets utilizing Gaussian mixture model (GMM)and Bayesian information criterion (BIC), and determined the convex envelope of each Gaussian model using a convex hull algorithm.The identified points within the convex set were thus esteemed as the boundaries, or frontier, of the presampled regions, and served as the starting structures for further simulations.The method was evaluated across three protein systems: Chignolin,maltodextrin binding protein(MBP),and the bovine pancreatic trypsin inhibitor(BPTI).It should be noted that although FEXS expands the sampling space,it sacrifices the Boltzmann distribution,because simulations restarting around the frontier points artificially boost the sampling probability of these regions.

Another strategy to accelerate the sampling of the conformational landscape through machine learning is to train a coarse-grained potential using all-atom simulation data.[72-74]Coarse-graining simplifies the molecular representations, reducing the level of detail and allowing for a broader and quicker exploration of conformational space.Popular coarsegraining approaches include MARTINI[75,76]and SARIH.[77]Clementiet al.reformulated coarse-graining as a supervised machine learning problem (named the CGNet) with the loss function built up by the standard terms of statistical estimator theory(bias, variance, and noise).[78]These terms have welldefined physical meanings and can be used in conjunction with cross-validation to select model hyperparameters (Fig.2(b)).On the basis of this work,Fabritiiset al.replaced the DenseNet architecture in CGNet by a more sophisticated graph neural network(GNN)framework,[79]and studied the folding of twelve fast-folding proteins[17]using the modified CGNet approach.For each protein, a separate neural network potential was trained and 32 individual coarse-grained simulations were performed using the trained potential.The simulations captured the native structure and reconstructed the reference free energy surface.In addition,the transferability of the GNN was demonstrated by training a multi-protein model using the reference simulation data of all twelve proteins,and applying it to 36 mutants of five selected proteins, given that the mutations did not affect the native structure of the protein.These simulations recovered the native conformations for those mutated proteins.

3.Autoencoders trained using molecular simulation trajectories for the exploration of protein conformational diversity

In order to further expand the conformational diversity of proteins, protein conformation generator models can be trained based on prior MD simulation trajectories.[80-83]These models contain neural network-based encoders that map protein conformations generated by prior MD simulations into dimension-reduced latent spaces (Fig.3(a)).The encoders are paired with reversed networks, i.e., the decoders, that,in principle, hold the capability to generate new, physically plausible protein conformations from random points in the latent space (Fig.3(b)), thereby complementing MD-sampled conformations.[84,85]

As a pioneer work, Degiacomi designed an autoencoder that maps coarse-grained models of protein conformations(encompassing backbone andβ-carbon atoms) into a twodimensional latent space.[85]Their network, composed of an encoder and a decoder each incorporating five DenseNet layers, was separately trained for each protein system using all-atom simulation trajectories.The training process minimized a loss function that assesses the structural similarity between simulation-produced and decoder-reconstructed conformations.Utilizing this network, latent representations of the HIV-1 capsid protein were learned based on a microsecondlong simulation of its unbound state.Through a 200×200 grid search in the latent space, several new, plausible conformations were identified by the decoder, which exhibited a lower RMSD from the bound state than that of the best model available within the simulation.Later, the same group refined the autoencoder model by substituting the five DenseNet layers constituting the encoder/decoder by six convolutional layers.[86]Additionally, the molecular potential of generated conformations was integrated into the loss function, ensuring the physical plausibility of the new conformations.This refined autoencoder was deployed to study the 438-residue MurD protein.The network was trained using two separate simulations that respectively covered the closed and open state conformations of the protein.The trained decoder predicted the transition state and a possible state transition path by interpolating the latent space between existing data points.To obtain physical interpretations for the latent space coordinates,Hayet al.utilized a simple,pre-defined low-dimensional conformational landscape to guide the network training.[87]As a proof-of-principle test, their method was tested on L-Ala13peptide and the 176-residue CaM protein,and was able to predict,with useful accuracy,conformations that were not present in the training data.It is important to note that only the top two principal components are selected as the latent space coordinates.However, this methodology may, in principle, be used with an arbitrary representation of the conformational landscape, which can consist of structural parameters of choice such as contact matrix, backbone dihedrals or a combination of specific physical parameters.

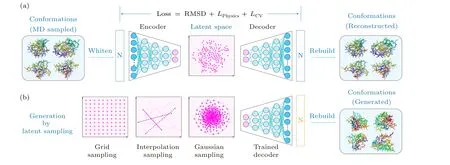
Fig.3.Illustration of the autoencoder frameworks designed for generating protein conformations.(a)The autoencoder architecture including an encoder and a decoder.(b)The workflow diagram of protein conformation generation using a well-trained decoder.

It is noted that all methodologies reviewed above have mostly been applied to structured proteins.Their application to unstructured proteins has been rarely explored, due to the highly dynamic conformations coupled with a complicated energy landscape.Recently,Zhouet al.tested the possibility of employing generative autoencoders that learn from short MD simulations to generate conformational ensembles of IDPs.[88]The heavy atom coordinates of an IDP were mapped into a latent space with the dimension reduced to 75%of its sequence length.Three proteins, Q15, Aβ40, and Chiz with sequence lengths of 15,40,and 64,were selected to test the efficiency of the autoencoder.The latent representations of protein conformations were fitted to a multivariate Gaussian model and decoded to generate full conformational landscapes.The generated conformations partially reproduced the small-angle x-ray scattering (SAXS) profiles and nuclear magnetic resonance(NMR)chemical shift data.However,these conformations exhibited a significant number of bond length and bond angle violations which should be refined by energy minimization,and reconstruction became more challenging as the IDP size increased.Later,Chenet al.improved the capability of the network for generating conformations of larger proteins,by substituting the autoencoder network with a more sophisticated VAE architecture.However,the performance of this improved network on IDPs (RS1, Aβ40, PaaA2, R17 andα-synuclein)remained lower compared to that on structured proteins(Ubiquitin and BPTI).Moreover, the quality of the generated conformations was heavily dependent on the diversity and quality of the samples obtained from preceding MD simulations.[89]

Overall, the protein conformational generators still have limitations in terms of the dependence of generated conformations on the quality of preceding MD simulations[88]and the difficulty in obtaining physical interpretations for latent coordinates.[90,91]Nevertheless,these methods possess the capacity to produce plausible protein conformations,albeit with a low probability, which could supplement those obtained from simulations.These generated structures may serve as new initial configurations for further simulations, potentially yielding a more comprehensive exploration of the protein conformational landscape.

4.Invertible network models for one-shot generation of protein conformations with correct Boltzmann weights

The decoder model of the aforementioned autoencoders,after being well-trained on simulation trajectories, is capable of generating physically realistic protein conformations not included in the training set.However, it falls short of providing the Boltzmann weight of the produced conformations,consequently lacking the capability to predict the energy landscape.One of the possible strategies to address this limitation is to use an invertible encoder network whose inverse inherently serves as a decoder.The encoder is trained to perform a coordinate transformation of the Boltzmann-weighted conformation distribution into a more navigable distribution,such as the Gaussian distribution.[92,93]Consequently, the encoder’s inverse naturally facilitates the transformation of Gaussiandistributed latent points into protein conformations with the correct Boltzmann weight.

One of the pioneering works in this field was the Boltzmann generator which was designed to generate unbiased oneshot equilibrium samples of representative condensed-matter systems and proteins, a groundbreaking contribution credited to No´eet al.[92]In their network model,the all-atom structure of a protein conformation was first decomposed into(i)main chain heavy atoms, represented by decorrelated and normalized Cartesian coordinates, and (ii) other atoms, represented by normalized internal coordinates (bond length, angles, and torsions with respect to parent atoms).Following this, the normalized coordinates were processed through a normalizing flow-based network,[94]comprising a number of real-valued non-volume preserving(RealNVP)layers.[95]The whole network transformed the Boltzmann-weighted protein conformations into a Gaussian-distributed, dimension-preserving latent space.The training of the Boltzmann generators was performed by a combination of train-by-energy and trainby-sample strategies.Specifically, a Gaussian sampling was conducted in the latent space to generate real-space samples whose free energies are evaluated by the Kullback-Leibler(KL) divergence[96](train by energy), and minimized using the adaptive stochastic gradient descent method (Adam).[97]Conformations generated by MD simulations were fed to the reverse of the generation network to produce latent coordinates whose distribution was compared with standard Gaussian distribution through a maximum likelihood (ML) method (train by sample).The generator was applied to generate low-energy structures of condensed matter systems and protein molecules in one shot, as shown for model systems and a millisecondtimescale conformational change of the BPTI protein.Additionally,a reaction coordinate(RC)loss could be added to promote the sampling of high-energy states in a specific direction of configuration for the calculation of the free-energy profile along a predefined RC.

It is imperative to note that to ensure inversibility, the Boltzmann generator does not diminish the dimension of the protein conformational space.Consequently,when applied to larger molecular systems,this approach precipitates an explosion of network parameters, leading to an increase of computational cost and difficulty in reaching equilibrium.For instance, a model with 768 hidden nodes per layer applied to a 106-residue bromodomain protein necessitates an overwhelming 959776800 learnable parameters.A reduction in the node number to 512 per layer may slightly reduce the parameter number to 629777440,but at the expense of the model expressivity.[93]One of the promising methods to reduce the model size while making minimal concessions in terms of model expressivity is the incorporation of coarse-grained representations.For instance, Lillet al.[93]developed a hierarchical normalizing flow-based generator that differs from the original Boltzmann generator in that, the protein conformations were described using the SIRAH coarse-grained model.Additionally,the RealNVP network was replaced by a rational quadratic neural spline flows(RQNSF)network which is more expressive and more accurate in predicting the conformational density.The applicability of the method has been tested on the one-shot configurational sampling of 106-residue bromodomain proteins,and on the folding/unfolding dynamics of the chignolin protein.

Although the development of the one-shot generation of protein conformations with correct Boltzmann weights is still at an early stage, it represents a direction of development in the field of ML-based protein conformational sampling.The Boltzmann generators and their subsequent refinements underscore a pivotal shift towards designing machine learning models that are capable of not only producing diverse and physically accurate protein structures,but also assigning their correct statistical weights.Although the application of these methods to more complex molecular systems,including IDPs,is still challenging, the continued evolution of these generative models holds the promise of revolutionizing the prediction accuracy and efficiency of protein conformational space and energy landscape.

Fig.4.Flowchart of the energy-function based invertible neural networks for the generation of Boltzmann weighted protein conformations.

5.Conclusion

This review has summarized recent advances in computational strategies that integrate machine learning with molecular simulations to aid the exploration of protein conformational landscapes.These strategies include the refinement of CV selections or the most promising sampling direction using machine learning,the generation of unsampled protein conformations based on unequilibrated simulations,and the one-shot generation of conformations with correct Boltzmann weights utilizing flow-based networks.These methods not only provide a promising pathway towards more efficient sampling of the vast conformational space of proteins,but also open a possibility for examining the impacts of mutations and other perturbations on protein structures and functions.

Yet, these methods are not without their limitations.Firstly, the need for a careful balance between model complexity and computational resources becomes increasingly apparent.Innovative solutions to reduce the dimensionality and parameter load,without compromising the accuracy of predictions,are essential for the application of these models to more complex protein systems.Secondly, there is a growing demand for models that can reliably handle the structural diversity and complex conformational landscape of biomolecules.Thirdly, the accuracy of these models, especially in the context of IDPs,depends heavily on the range and quality of conformations sampled in preceding MD simulations which are taken as training sets.As the field progresses, the pursuit of more accurate, efficient, and universal methods is crucial for the in-depth understanding of protein conformational spaces,and will inevitably contribute to the broader objectives of computational biology,such as drug discovery,enzyme design,and the unraveling of the molecular basis of heath and diseases.

Acknowledgments

Project supported by the National Key Research and Development Program of China (Grant No.2023YFF1204402),the National Natural Science Foundation of China (Grant Nos.12074079 and 12374208), the Natural Science Foundation of Shanghai (Grant No.22ZR1406800), and the China Postdoctoral Science Foundation(Grant No.2022M720815).