Anomalous spin Josephson effect in spin superconductors

Wen Zeng(曾文) and Rui Shen(沈瑞)

1School of Physics and Electronic Engineering,Jiangsu University,Zhenjiang 212013,China

2Jiangsu Engineering Research Center on Quantum Perception and Intelligent,Detection of Agricultural Information,Zhenjiang 212013,China

3National Laboratory of Solid State Microstructures and School of Physics,Nanjing University,Nanjing 210093,China

4Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China

Keywords: tunneling junction,spin supercurrent,0-π transition,anomalous spin Josephson effect

1.Introduction

The exciton condensates are composed of the electronhole pairs which are charge neutral while their spin may either be singlet or triplet.[1,2]The key issue to realize the stable exciton condensates is to prevent the electron-hole recombination.[3,4]Many strategies have been proposed to do so, such as the exciton condensates realized in the doublelayer systems,[5-8]where two monolayers are spatially separated by an insulator layer.The insulator is supposed to be high enough to prevent the electron-hole recombination.Recently,Sunet al.[9,10]suggested that the stable spin-polarized triplet exciton condensates could be realized in the graphene monolayer growing on a ferromagnetic material or under an external magnetic field,where the electron-like spin-up states are below the hole-like spin-down states,[9]which prevents the electron-hole recombination and means the exciton condensates in the ferromagnetic graphene system are stable.These stable exciton condensates are termed as the spin superconductor states.[9,10]Analogous to the Andreev reflection in charge superconductors,[11-16]Lvet al.[17]studied the Andreev-like reflection in the normal metal/spin superconductor(NS)junctions based on the ferromagnetic graphene,where an incident spin-up electron is reflected as a spin-down electron and the spin 2×(¯h/2) is injected into the spin superconductor.This spin-flipped Andreev-like reflection leads to the spin current when a spin voltage is applied across the junction.

Inspired by this, in this paper we investigate the spin Josephson effect in the device consisting of two weakly coupled spin superconductors with noncollinear spin polarizations.Both the out-of-plane spin polarization configuration and the in-plane spin polarization configuration are considered, as shown in Figs.1(a) and 1(b), respectively.We show that the repeated spin-flipped Andreev-like reflections at the NS interfaces lead to the Andreev-like bound states,which are responsible for the dissipationless spin supercurrent.This spin supercurrent is driven by the macroscopic phase differenceφs,which origins from a spin current flowing through the junction under the drive of an external device or from a variation of an external electric field thread the ring junction device.[9]As the condensed electron-hole pairs in spin superconductors are charge neutral,the charge current in our model is zero.For the Josephson junctions with out-of-plane spin polarizations,the possibleπ-state spin supercurrent can be generated due to the Fermi momentum-splitting Andreev-like reflections at the NS interfaces.The anomalous spin supercurrent is absent and the phase of the spin supercurrent is determined by the Fermi level and the junction length.For the Josephson junctions with in-plane spin polarizations,the misorientation angle of the inplane polarizations acts as an effective superconducting phase,leading to a finite spin superconducting current at zero phase difference, which is termed as the anomalous spin Josephson effect.Furthermore,the symmetry analysis shows that the appearance of the anomalous spin Josephson current is possible when the combined symmetry of the spin rotation and the time reversal is broken.

Fig.1.Schematic of the spin Josephson junctions with the length of the normal region being L.The red arrows denote the directions of the spin polarization of the triplet exciton condensates.The red and blue wavy lines denote the left-propagating spin-up electron and the rightpropagating spin-down electron, respectively.(a) The spin Josephson junction with out-of-plane spin polarization.The spin polarization of the triplet exciton condensate in the left spin superconductor is along the z axis and the spin polarization of the triplet exciton condensate in the right spin superconductor lies in the y-z plane with the polar angle θm.(b)The spin Josephson junction with in-plane spin polarization.The spin polarization of the triplet exciton condensate in the left spin superconductor is along the x axis and the spin polarization of the triplet exciton condensate in the right spin superconductor lies in the x-y plane with the azimuthal angle φm.

The remainder of the paper is organized as follows.The model Hamiltonian and the scattering approach are explained in detail in Section 2.The numerical results and discussion are presented in Section 3.Finally,we conclude in Section 4.

2.Model and formulation

2.1.Model Hamiltonian

The model Hamiltonian for the spin superconductor with the spin polarization alongzaxis is given by[9,17]

where the spin rotation matrix is given by

withτ0being the identity matrix in the pseudospin space,θmandφmbeing the polar angle and the azimuthal angle,respectively.

We consider the spin superconductor/normal metal/spin superconductor junctions in thex-yplane,where the spin polarizations of the two spin superconducting regions are noncollinear,as schematically shown in Fig.1.The junction is described by the Bogoliubov-de Gennes(BdG)Hamiltonian,[22]which is given by

whereℋL=ℋS(nL)Θ(-x),ℋR=ℋS(nR)Θ(x-L) andℋN=ℋS|Δ→0Θ(x)Θ(L-x)withnL(R)being the spin polarization for the left(right)spin superconductor andΘ(x)being the Heaviside step function.The superconducting pair potential isΔs=Δe-iφs/2forx ＜0 andΔs=Δeiφs/2forx ＞L,whereφsis the phase difference across the junction.

2.2.Transfer matrix

The scattering states of the spin superconductor with spin polarizationncan be obtained by

Due to the spin-flipped Andreev-like reflection at the NS interface,[17]the incident and reflected states are connected byψ¯σ=SψσwithSbeing the transfer matrix,ψσ(ψ¯σ)being the spin-σ(spin-¯σ)component in Eq.(7)(¯σ ≡-σ).The transfer matrices at the left and right interfaces can be directly obtained by matching the left and right propagating states in Eq.(7),respectively,which are given by

withν= + (-) for the left (right) interface.S(0)νis the Andreev-like transfer matrix forθm=0,which is given by

wherek=kFcosαis the longitudinal wave vector in the normal region withkF=µ/(¯hvF) being the Fermi wave vector andα=arcsin(¯hvFky/µ)∈[-π/2,π/2]is the incident angle.

The total spin Josephson current density can be obtained by[24,25]

wherekBis the Boltzmann constant,Tis the temperature,and the energy variable in the determinant is replaced by iωnwithωn=(2n+1)πkBT(n ∈Z).

3.Results

In the following calculations, we setΔ=1 meV as the energy unit.The superconducting coherence length isξ=¯hvF/Δ ≈360 nm,which is set as the length unit.

3.1.Josephson junction with out-of-plane spin polarization

The Josephson junction with the out-of-plane spin polarization is schematically shown in Fig.1(a),where the spin polarization in the left superconducting region is along thezaxis and the spin polarization in the right superconducting region lies in they-zplane with the polar angleθm.The Andreevlike transfer matrices at the NS interfaces are given by

whereEℓis the positive root of Eq.(15)andWis the width of the junction.

The supercurrent-phase relations at differentθmare shown in Fig.2(a)forkFL=0.1.The spin Josephson current decreases with the increase ofθm,and drops to zero when the spin polarizations in the left and right superconducting regions are antiparallel,i.e.,θm=π.In this antiparallel configuration,the spin polarizations of the spin-triplet electron-hole condensations in the left and right spin superconductors are opposite,the Andreev-like process between two NS interfaces can not form a closed loop.Consequently,theφs-dependent Andreevlike levels are absent,leading to the zero spin supercurrent.

ForkFL= 2, the spin supercurrent is reversed and theπ-state Josephson junction appears, as shown in Fig.2(b).This 0-πphase transition is attributed to the Fermi-momentum splitting Andreev-like reflections at the NS interfaces.At the Fermi surface,the right-propagating spin-up electron with the wave vectorkFis converted into a left-propagating spin-down electron with the wave vector-kFdue to the Andreev-like reflection, leading to the wave vector differenceΔk=2kF.An additional phase shift 2kFLis accumulated in a closed Andreev loop.The total scattering phase acquired by the electrons in this closed Andreev loop is 2kFL±φs-2arccos(E/Δ),[26]which should be quantized according to the quasiclassical Bohr-Sommerfeld quantization condition,[27,28]i.e., 2kFL±φs-2arccos(E/Δ)=2πn(n ∈Z).Consequently, the state of the junction can be controlled by the phase factor cos(kFL).The spin supercurrent can be expressed asj∝cos(kFL)sinφs.For 2nπ+π/2＜kFL ＜2nπ+3π/2,the spin supercurrent is reversed.

The critical spin current defined byjc=max|j(φs)|as a function of the junction lengthLis shown in Fig.2(c).Due to the additional phasekFL, the critical spin current is proportional to cos(kFL), which exhibits an oscillation behavior as the junction length increases.Forµ=0.5Δin Fig.2(c),the oscillation period can be estimated asTL=π/kF=2πξ.The critical spin current as a function of the polar angleθmis shown in Fig.2(d).Theθm-dependent critical spin current is symmetric due to the rotation symmetry,i.e.,jc(θm)=jc(-θm).The critical spin current reaches its maximum value atθm=0 and becomes zero atθm=±π.

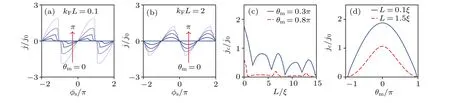
Fig.2.(a), (b) The current-phase relation for the Josephson junctions with the out-of-plane spin polarization.The red arrows indicate the curves with the increasing deviation of the relative angles θm, which change from 0 to π with a step of π/4.(c)The critical spin Josephson current density jc as a function of L for θm=0.3π(solid)and θm=0.8π(dashed).The Fermi level isµ=0.5Δ.(d)The critical spin Josephson current density jc as a function of θm for L=0.1ξ (solid)and L=1.5ξ (dashed).Both j and jc are renormalized by j0=µΔW/(2π¯hvF).

3.2.Josephson junction with in-plane spin polarization

The Josephson junction with in-plane spin polarization is schematically shown in Fig.1(b),where the spin polarization in the left superconducting region is along thexaxis and the spin polarization in the right superconducting region lies in thex-yplane with the azimuthal angleφm.The Andreev-like transfer matrices are given by

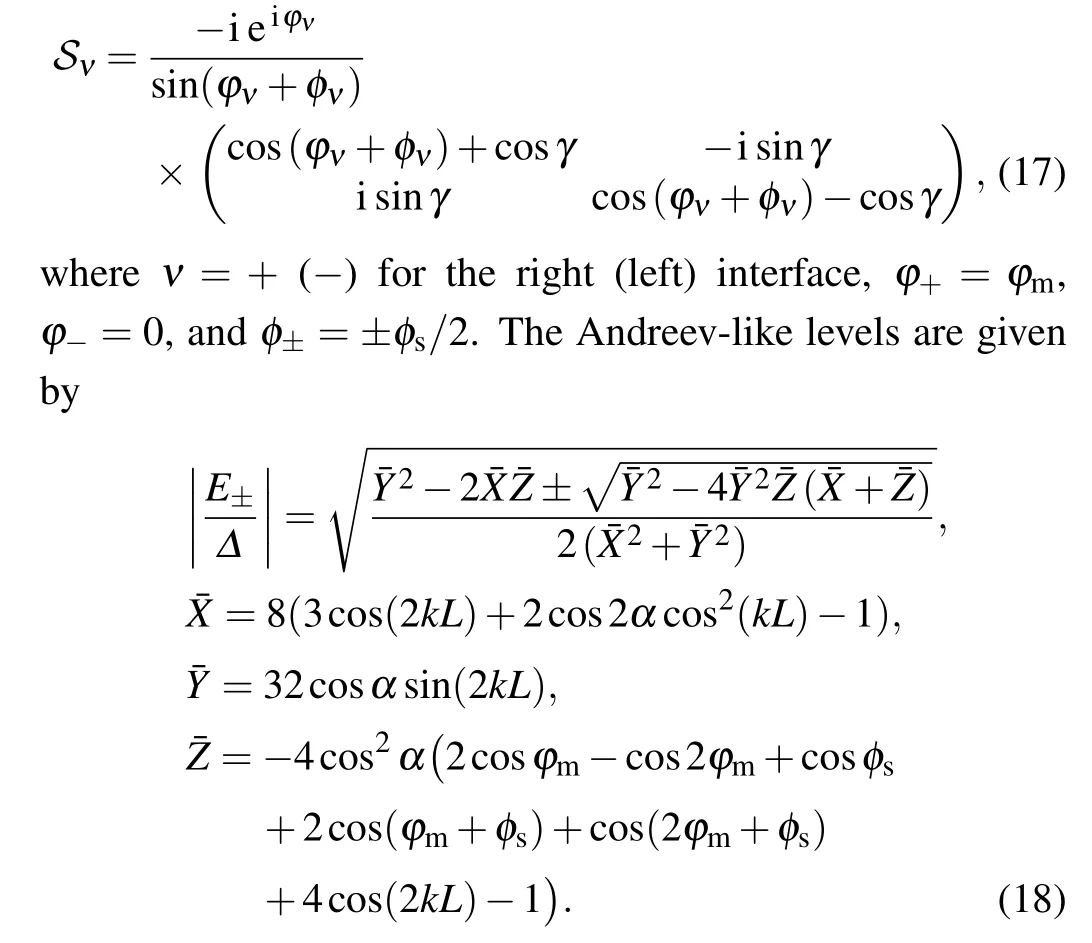
The zero-temperature spin Josephson current obtained by Eq.(16)is shown in Fig.3(a)atkFL=0.1.Due to the spin rotation symmetry,the spin supercurrent for the Josephson junctions with parallel in-plane spin polarization (φm=0) is the same as that for the Josephson junctions with parallel out-ofplane spin polarization(θm=0).For the antiparallel in-plane polarization(φm=π),the spin Josephson current is absent due to the absence of theφs-dependent Andreev-like levels.

Forφm̸=0 andφm̸=π, the anomalous spin Josephson currentj|φs=0appears, as shown in Fig.3(a).For simplicity,we present the spin Josephson current for the one-dimensional(1D)case withky=0

which can imply the qualitative properties of the twodimensional Josephson junctions.Equation (19) shows that the anomalous spin Josephson current atφs=0 is proportional to cos(kFL)cos2(φm/2)sinφm.The spin Josephson current can be reversed by the additional phase factor cos(kFL).ForkFL=2, the reversed spin Josephson current obtained from Eq.(16)is shown in Fig.3(b).

Fig.3.(a),(b)The current-phase relation for the Josephson junctions with the in-plane spin polarization.The red arrows indicate the curves with the increasing deviation of the relative angles φm,which change from 0 to π with a step of π/4.(c)The critical spin Josephson current density jc as a function of L for φm =0.3π (solid) and φm =0.8π (dashed).The Fermi level is µ =0.5Δ.(d) The critical spin Josephson current density jc as a function of θm for L=0.1ξ (solid)and L=1.5ξ (dashed).Both j and jc are renormalized by j0=µΔW/(2π¯hvF).

The critical spin currentsjcas a function of the junction lengthLand the azimuthal angleφmare shown in Figs.3(c)and 3(d), respectively.TheL-dependent oscillation is determined by the additional phase factor cos(kFL) due to the Fermi-moment splitting.For a fixedL, theφm-resolvedjcis symmetric,as shown in Fig.3(d).

The anomalous spin Josephson currentj|φs=0as a function ofLis shown in Fig.4(a).Forφm=0 andφm=π, the anomalous Josephson effect is absent.Forφm̸=0 andφm̸=π,j|φs=0oscillates with the increase ofLand has the same oscillation period asjc.Forµ=Δin Fig.4(a), the oscillation period is aboutπξ.j|φs=0as a function ofφmis shown in Fig.4(b).Theφm-resolved anomalous spin Josephson current is asymmetric and satisfies the relation

due to the symmetry of the BdG Hamiltonian, which is explained in detail in Subsection 3.3.

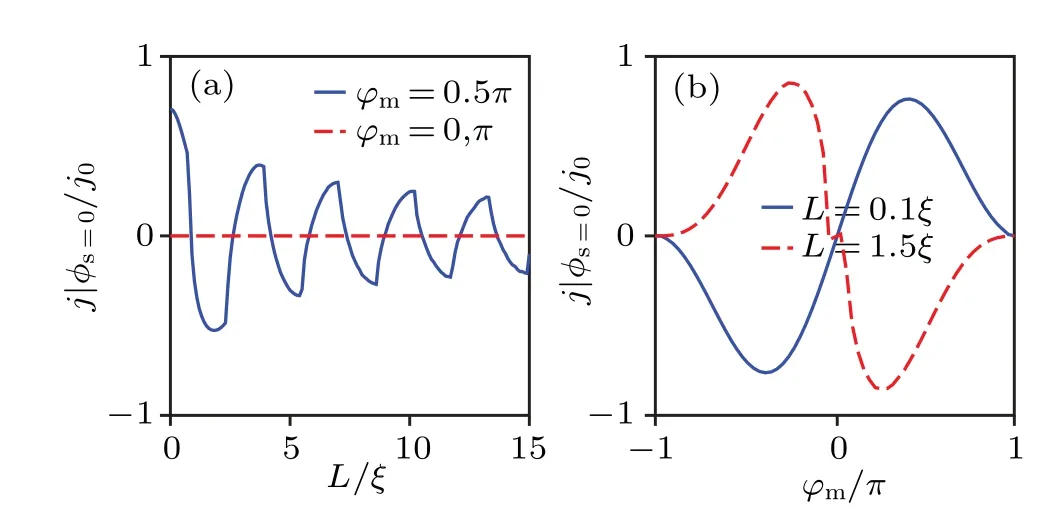
Fig.4.(a) The anomalous spin Josephson current density j|φs=0 as a function of L for φm=0.5π (solid)and φm=0,π (dashed).The Fermi level is µ =Δ.(b) The anomalous spin Josephson current j|φs=0 as a function of φm for Lm =0.1ξ (solid)and L=1.5ξ (dashed). j|φs=0 is renormalized by j0=µΔW/(2π¯hvF).

3.3.Symmetry analysis

The Hamiltonian of the spin superconductor with out-ofplane spin polarization can be written as

where ¯η=-η,T= iσyτzCis the time-reversal operator withCbeing the complex conjugation.For thek-independent Hamiltonianℋ′(φs,θm),considering the combined symmetryP=σyTwithσybeing the spin rotation symmetry andTbeing the time-reversal symmetry,one finds that

Due to the spin degeneracy in pristine graphene,hη(k)remains unchanged underP.Consequently, with the help of Eq.(6),the BdG Hamiltonian for the Josephson junctions with the outof-plane spin polarization holds the relation

The symmetryPis broken and the BdG Hamiltonian holds the relation

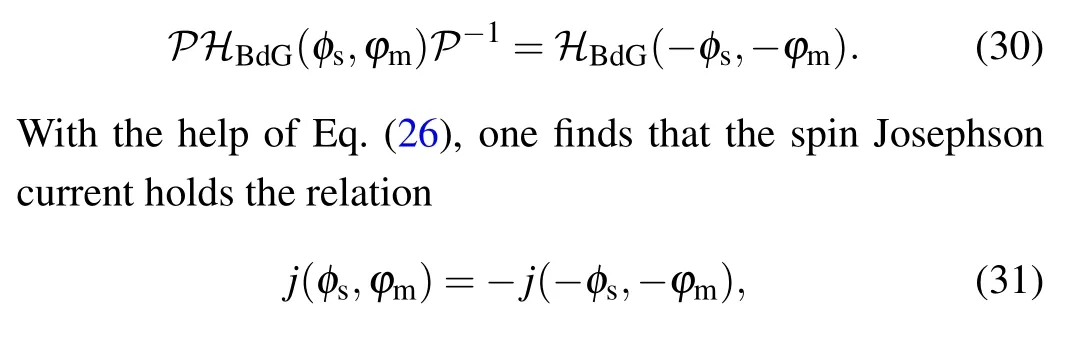
leading to the presence of the anomalous spin Josephson current.The anomalous spin Josephson current is an odd function ofφmsatisfyingj|φs=0(φm)=-j|φs=0(-φm), as shown in Fig.4(b).

In fact,the anomalous Josephson effect is possible when the symmetriesT,DandPare all broken,[31,32]whereD=σyRxzTis another combined symmetry withRxzbeing the mirror reflection about thex-zplane.We note that the symmetriesTandDare always broken in our model for both the out-ofplane spin polarization and the in-plane spin polarization.The combined symmetryPplays a key role in our model: For the Josephson junction with out-of-plane spin polarization,the absence of the anomalous spin Josephson current(j|φs=0=0)is protected byP.For the Josephson junction with in-plane spin polarization, the breaking ofPleads to the presence of the anomalous spin Josephson current.

4.Conclusions

To conclude,we theoretically investigate the spin Josephson effect in the spin superconductor/normal metal/spin superconductor junctions, where the spin polarizations of the left and right spin superconducting regions are noncollinear.For the Josephson junctions with out-of-plane spin polarization,the possibleπ-state spin supercurrent can be generated due to the Fermi momentum-splitting Andreev-like reflection at the normal metal/spin superconductor interface.For the Josephson junctions with in-plane spin polarization, the anomalous spin supercurrent appears and is driven by the misorientation angle of the in-plane spin polarization.The symmetry analysis shows that the appearance of the anomalous spin Josephson current is possible when the combined symmetry of the spin rotation and the time reversal is broken.

Acknowledgement

Project supported by the National Key R&D Program of China(Grant No.2022YFA1403601).