Enhanced measurement precision with continuous interrogation during dynamical decoupling
2024-03-25JunZhang张军PengDu杜鹏LeiJing敬雷PengXu徐鹏LiYou尤力andWenxianZhang张文献
Jun Zhang(张军), Peng Du(杜鹏), Lei Jing(敬雷), Peng Xu(徐鹏),Li You(尤力), and Wenxian Zhang(张文献),3,†
1Key Laboratory of Artificial Micro-and Nano-structures of Ministry of Education,and School of Physics and Technology,Wuhan University,Wuhan 430072,China
2State Key Laboratory of Low-Dimensional Quantum Physics,Department of Physics,Tsinghua University,Beijing 100084,China
3Wuhan Institute of Quantum Technology,Wuhan 430206,China
Keywords: quantum sensing, continuous interrogation, quantum magnetometer, dynamical decoupling,Heisenberg limit
1.Introduction
As one of the most studied control methods, dynamical decoupling (DD) can actively suppress noise to preserve coherence of a quantum system,[1,2]e.g., in trapped ions,[3-7]solid-state spins,[8-15]superconducting quantum circuits,[16-18]and ultracold atomic gases.[19-22]Despite its successes,DD has found only a few usages in precision measurement of a DC signal.[23]While unwanted and unknown stochastic noises are suppressed by periodically refocusing a quantum state to the initial one with DD,[19,24]a DC (or low frequency AC) signal sensed from phase interrogation by a quantum state provides no net accumulated phase.[25]Such a dilemmatic situation is unfortunate,especially since the effect of achieving beyond standard quantum limit (SQL) precision could obviously benefit from entangled or squeezed quantum states that are otherwise easily decohered.[26-32]
This work studies the application of DD to precision measurement by suppressing noise while reaping up a gain from continuous sensing of a weak DC (or low frequency AC) signal.[25]To explain our idea, let us recall an athlete in a 5-10-5 shuttle run.After start, his/her displacement increases while running forward.When he/she comes around after touching the turn-around lines, however, the displacement with respect to the initial line decreases and eventually becomes zero upon returning back to the start line, although the net distance covered continuously grows after repeated line touchings at both ends.Analogously, the interrogated signal and the accompanying noise accumulate during the first half of a DD cycle, but are both compensated for by the complementary second half period.To obtain a net phase accumulation of a DC signal, one could simply flip the signal’s phase but not that of the noise during the second half as illustrated in Fig.1, provided the signal was known.Such a simple (alternately repeated) phase flip could help to recover the DC signal by allowing the consequent interrogation to last for many DD cycles while the noise remains suppressed.We refer the above described manipulation protocol as the phase relay method(PRM).If implemented this way,DD,which has been demonstrated successfully for high frequency AC signal measurements in a variety of physical systems,[4,14,15,19,24,33-38]will also be applicable to the measurement of DC (and lowfrequency AC)signals.
2.Continuous interrogation during DD
We illustrate the PRM by applying it to measure a weak DC magnetic field using an atomic spinor Bose-Einstein condensate through Ramsey interferometry.[39]The condensate is assumed to consist ofN=1000087Rb atoms, which comes with a strong repulsive spin independent interaction in addition to a weak ferromagnetic spin exchange interaction.For small or moderate sizedNand with the condensate in an optical trap,its Hamiltonian under the single spatial mode approximation reduces toH=-c′2J2+γB·J,after constant terms are dropped,[40,41]wherec′2denotes the spin exchange interaction strength with the collective condensate spinJ=∑Ni=1Fifrom spinFiforith atom,γthe atomic gyromagnetic ratio,andBthe total magnetic field which possibly includes a fixed known bias fieldB0,a fixed weak but unknown DC magnetic fieldb0(the signal to be measured),and stray stochastic magnetic fieldb(noise)to be suppressed by DD.We consider the simple case of the bias and the signal field along the samezaxis direction, while the stray field is randomly directed with random amplitude(|b|<bcupto a cutoff amplitudebc).
2.1.Noise suppression with uniaxial DD
The condensate spin decoheres by the stray magnetic field,which eventually limits the optimal achievable sensitivity of the magnetometer.Although the dephasing noise model may give analytical results as derived in Appendix B,we consider a more realistic stray-field model.Including the stray magnetic field,the Hamiltonian becomes
wherebx,y,z ∈[-bc,bc]and a bias fieldB0≫b0,cis required.To suppress decoherence from the stray field, many DD schemes can be applied.[2,42-50]We adopt a uniaxial DD protocol which is robust and easy to implement experimentally.[51]
Here we emphasize that the spin exchange termc′2J2is the natural ingredient of the spinor BEC, and thus it can not be excluded from the Hamiltonian (1), even though it has no contribution to the results of our calculation.Specifically,we consider a ferromagnetic interactionc′2<0,which ensures the validity of the single mode approximation utilized in deriving the system Hamiltonian.
By denoting theπ-pulse alongx-axis byX, the evolution operator for a unit cycle becomesU2τ=XUτXUτ=exp(-i2τ¯H), whereUτ= exp(-iτH) withτthe duration between pulses and ¯Hthe time averaged Hamiltonian over a whole cycle.Under the magic conditionτ=2mπ/(γB0)(form=1,2,3,...),the uniaxial DD is capable of efficiently suppressing decoherence from the stray magnetic field, because the effective coupling between the condensate spin and the stray magnetic field is reduced by a factor of(bz/B0),leading to ¯H ≈-c′2J2+(bz/B0)γbyJy.[51]Further suppression of the stray magnetic field is achieved if a refined uniaxial DD protocol,the balanced uniaxial DD(BUni-DD)[X¯UτX¯UτXUτXUτ],is employed,whereUτ(¯Uτ)denotes free evolution with a positive (negative) bias field.The latter leads to the BUni-DD periodT=4τand the magic conditionγB0τ=2mπremains needed.It is easy to find that the average Hamiltonian further improves to ¯H ≈-c′2J2+O((bc/B0)2).
2.2.Phase relay method
To estimate the signal field amplitude with Ramsey interferometry,the condensate spin is initially prepared to align alongx-direction.During the interrogation timet,it processes along the direction of the bias and signal field sum which provides an accumulated time phaseφ=γ(B0+b0)twithB0=|B0| andb0=|b0|.By measuring precisely this phaseφat timet, the signal field can be determined.Experimentally, this is accomplished by measuringJy, they-component of the collective spin, which oscillates with time as shown in Fig.1.The estimated phase between 0 and 2πis extracted by fitting the observed data to a sinusoidal function.For longer interrogation time, this phase will exceed 2π.Consequently,one would hope to keep track of indexing the number of oscillation cycles in order to continuously interrogate a monotonically increased phase instead of a zigzagged one chopped into[0,2π].During interrogation,the stray magnetic field stochastically disturbs the measured phase and introduces an uncertainty Δφ, which leads to an uncertainty in the signal Δb0.Such effects from the stray magnetic field can be suppressed by periodically executed DD pulses,for example,with instantaneousπrotations of the spin alongx-axis, or spin flips.As numerical results verified in Fig.1,effects of the noise are indeed suppressed significantly.Unfortunately,the interrogated phase from the bias plus the signal field is also refocused by the above DD pulses, i.e., the net phase accumulation after complete cycles of DD diminishes,making it difficult to estimate the signal field.
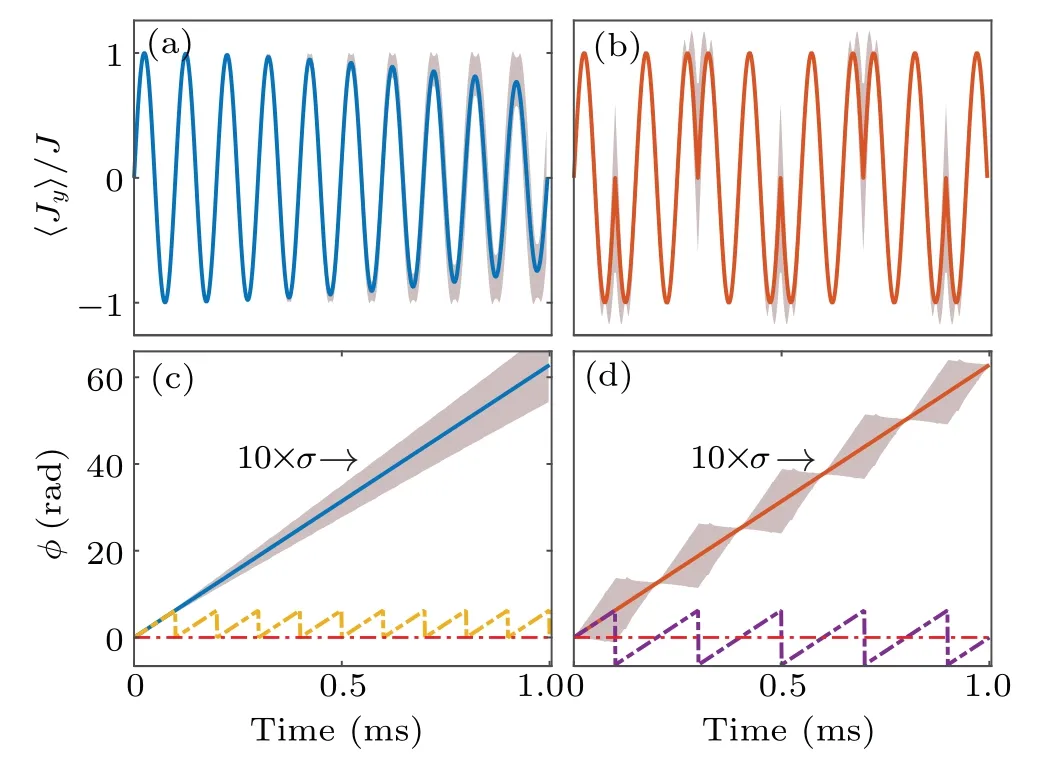
Fig.1.Phase relay method.(a)Numerically simulated mean(blue solid line)and the standard deviation(gray shaded region)for observable Jy without DD.(b) The same as in (a) but with DD shown by the red solid line (mean) and the gray shaded region (one standard deviation).The applied pulse interval is τ =0.1 ms.The standard deviation is found to be strongly suppressed after one DD cycle T =4τ.(c)Phase φ extracted directly from the simulation(a) (yellow dash-dotted line)and with hypothetical accumulation taking into account the indexed number of oscillations(blue solid line).The standard deviation of the phase (shaded in gray) is multiplied by 10 for better viewing.The phase increases linearly and the standard deviation grows monotonically with time.(d)Phase extracted directly from the experimental observable(b)(purple dash-dotted line) and after applying the PRM (red solid line).The standard deviation of the phase(shaded gray)is multiplied by 100.Similarly,the phase after PRM increases linearly and the standard deviation is strongly suppressed after each DD cycle.
While BUni-DD protocol discussed above suppresses the stray magnetic field,the signal field is also suppressed unfortunately as the accumulated phase nearly zeros out after each DD cycle.However,the signal field differs from the stray magnetic field because it is by definition nonzero and we further note that the pulse interval for the DD pulse sequenceτis exactly known.These features(knowledge)provide us an opportunity to continuously accumulate the phase associated with the signal by the phase relay method(PRM),inspired by the 5-10-5 shuttle run.
We now examine the interrogated phase accumulation associated with the signal in the first DD cycle,over a period of 4τ(see Fig.2).For the sake of clarity, we neglect the stray magnetic field at this stage.During the first quarter,the phase of the signalφs(τ)=γb0τaccumulates linearly.Att=τ,an instantaneousXpulse then flips the condensate spin and the phase changes to-φs(τ).During the second quarter,the signal’s phase evolves linearly back to 0, i.e.,φs(2τ)=0.This phase pattern repeats in the third and the fourth quarters as in the first and the second quarters,respectively.The total interrogated phase during a whole DD cycle vanishes.
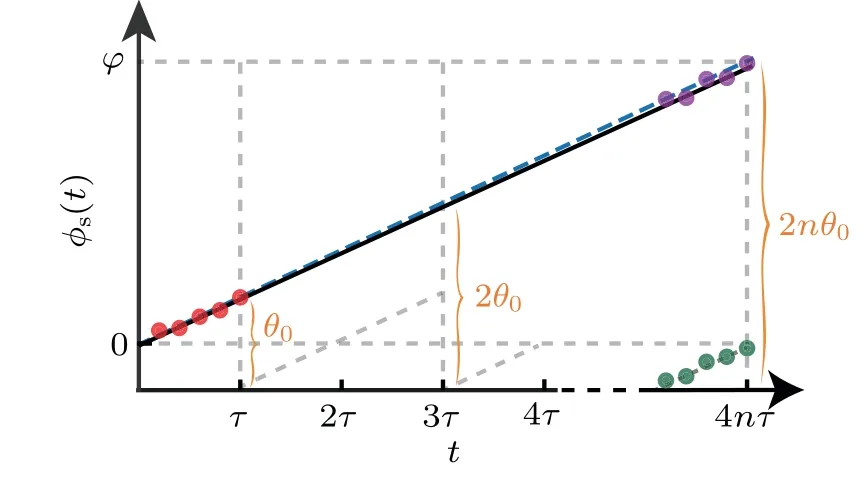
Fig.2.The PRM protocol.A roughly estimated phase-shift θ0 is obtained by linear least square fitting (red dots) to a few data points extracted from preliminary measurements of the observable during the first quarter period.One then extracts estimated phases φs(t) (green dots)and shifts them according to θ0 and the cycle indexing number n(purple dots), during the whole BUni-DD sequence.The blue dashed line illustrates the relayed phase based on the preliminary estimated θ0.An improved estimate for θ0 is obtained by a least square linear fit to all the relayed data from many BUni-DD cycles(black line).The slope of the fitted black line denotes a refined estimate of the signal field b0.
As shown in Fig.2,an immediate method to continuously interrogate the signal phase during the BUni-DD cycle is to shift the phase duringt ∈[τ,3τ]by a fixed amountθ0and by 2θ0during the last quartert ∈[3τ,4τ] respectively, providedθ0=γb0τfrom the signal fieldb0was known.For thenth DD cycle,the required phase shift of the first quarter becomes(2n-2)θ0,the second and the third quarter(2n-1)θ0,and the fourth quarter 2nθ0.In practice,we would first obtain a crude estimate to the phase shiftθ0by running a few preliminary experiments without DD pulses, then followed by optimizations, and finally determineθ0more precisely.One plausible approach is shown in Fig.2 which obtains the shifted phase data(by varyingθ0)during the first and the last quarters of the whole DD sequence, and optimizes with least square fitting.Afterwards,a refined and more accurateθ0may be determined and likewise the signal field is determined more precisely.
Including the stray magnetic field, our numerical simulations confirm that the PRM remains effective.For practical implementations, the PRM protocol can be summarized explicitly by the following steps.
(i) Take a few measurements of〈Jy〉 to obtain〈Jy〉(t) at short time.
(ii) Extract the phaseφs(t) from the experiment data, fit linearly the phase-time curve,and find out a crude estimate for the phase-shiftθ0,which is similar to the adjustment of fire in military.
(iii)Take more measurements of〈Jy〉(t)at the beginning,in the middle,and at the end of the BUni-DD sequence.
(iv)Extract phasesφs(t)from the larger data set,and relay/shift measured phases accordingly with the knowledge of the cycle indexing numbernandθ0.
(v)Optimizeθ0with a least-square linear fit.
(vi)Derive the signal fieldb0.
With the PRM,the phase relays continuously during a DD cycle,as shown schematically in Fig.1,which can be further optimized by least square fitting the data over many DD cycles.Consequently, the net phase from the bias and signal fields continuously integrates while the stochastic contributions from noise are averaged out after repeated DD cycles,thus the measurement precision of a weak DC signal is enhanced.
3.Heisenberg limit magnetometer with spin squeezing
To evaluate the achievable precision after an interrogation timet, we calculate the signal-field sensitivity for measuring the weak magnetic field according to

We consider an SSS with averaged spin point along thexaxis,while the squeezing direction is along they-axis,orthogonal to the averaged spin.Such a state is readily prepared experimentally in a spinor87Rb atomic condensate.[28,52,53]We setω0=γB0=2π×10 kHz corresponding to a bias field ofB0=14.3 mG(γ=0.70 MHz/G).The cutoff field is taken to be at a nominal laboratory noise levelbc=0.1 mG (with an angular frequency 2π×70 Hz).As for the signal,we assumeb0=1.6µG,which serves to demonstrate quantum enhanced precision.The pulse interval of BUni-DD isτ=0.1 ms, satisfying the magic conditionω0τ=2π.After repeated simulation runs with random stray magnetic fieldbof uniformly distributed componentsbx,y,z ∈[-bc,bc], we compute the observable〈Jy〉and its standard deviation,extract the phase,derive the signal’s phase and its standard deviation, and finally determine the sensitivityη(Fig.3).

Fig.3.Precision measurement of a weak DC magnetic field with DD.(a),(b) The average condensate spins (solid lines) and their standard deviations(gray shaded areas)for initial coherent spin state(CSS)versus squeezed spin state (SSS).(c), (d) The signal’s phases φs extracted with PRM from simulated experimental observables in(a)and(b),respectively with b0=160µG in (c) and b0 =1.6 µG in (d).The bias and the cutoff fields are assumed to be B0 =14.3 mG and bc =0.1 mG, respectively.The small standard deviations are multiplied by 50 in order to be clearly visible.(e)The signal field’s sensitivities under DD for CSS(green circles)and SSS(purple triangles),respectively approaching the SQL(black solid line)and HL(red solid line).For comparison,we present the sensitivities without DD pulses for both CSS(blue squares)and SSS(red diamonds)as well in the same figure.The DD pulses are seen to strongly suppress noise and significantly improve sensitivity.



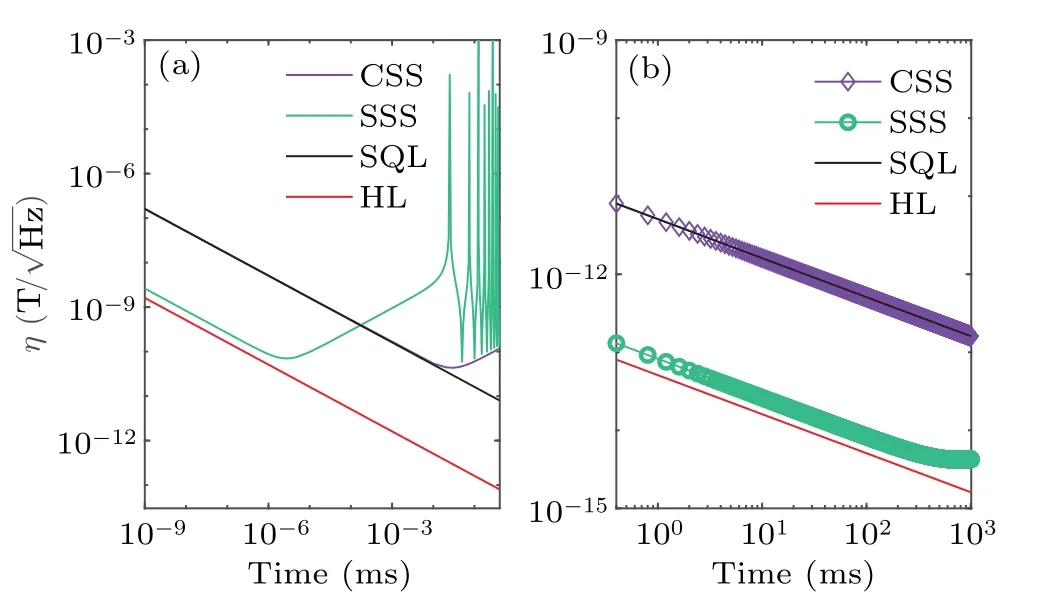
Fig.4.Sensitivity at short and long times for CSS(purple line)and SSS(green line).The cutoff field assumed bc =0.1 mG.Both states decohere quickly without the application of BUni-DD(a)but maintain their coherence for longer times with the application of BUni-DD (b).The black and the red lines denote SQL and HL,respectively.
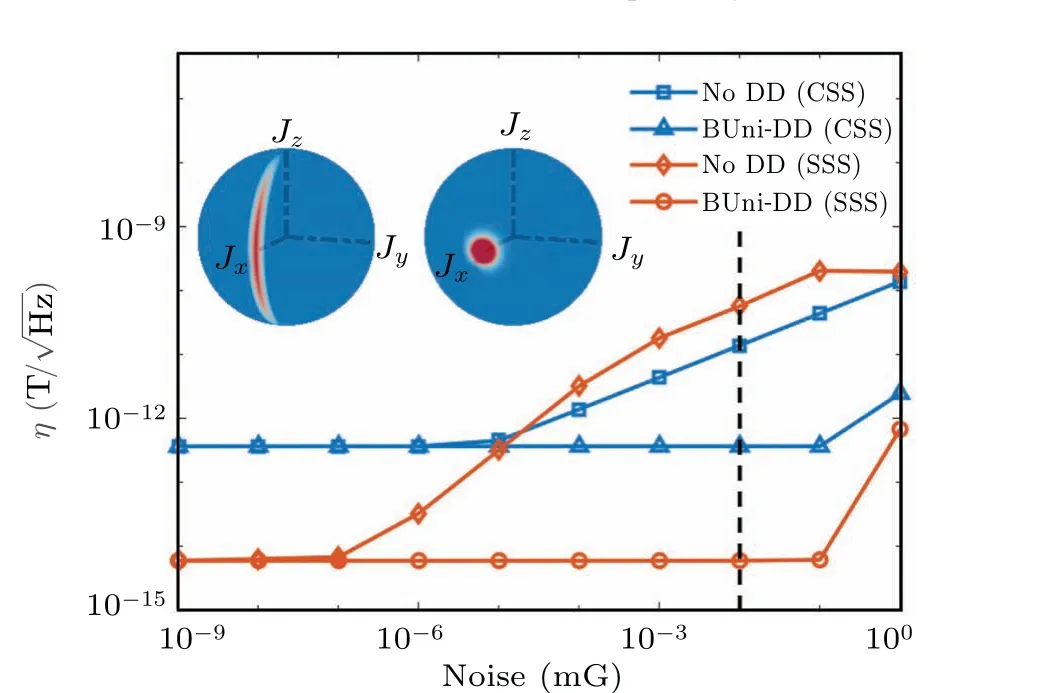
Fig.5.Optimal sensitivities within 200 ms of interrogation time at different noise levels.The optimal sensitivities detected by an initial CSS with (without) DD pulses are denoted by blue triangles (squares); the ones detected by an initial SSS with (without) DD pulses are shown with orange circles (diamonds).As long as the stray magnetic field is lower than the noise threshold ~0.1 mG,noise is strongly suppressed and sensitivities with DD are independent of the noise strength.For comparison, the noise thresholds without DD pulses are numerically found to be ~10-6 mG for an initial CSS and ~10-8 mG for an initial SSS.The vertical line marks a laboratory noise level of 0.01 mG.[19]


4.Discussion and conclusion
In conclusion, we propose the PRM which enables continuous interrogation during DD and enhances the system’s coherence during quantum measurements.With this PRM,we numerically show that the sensitivity of a spinor-BECbased magnetometer approaches the SQL with an initial CSS and the HL with an SSS.Remarkably, the simulated optimal sensitivity with only 10000 atoms enters the regime of a fewwithin 200 ms interrogation time, indicating the great potential of enhanced quantum metrology utilizing the spin squeezing and the metrologically-useful-quantum entanglement.The PRM applies not only to the investigated spinor-BEC magnetometer,[19,20]but also to other quantum sensor systems suffering severe decoherence, such as nitrogen vacancy centers in diamond,[8-10,12,13,15]trapped ions,[4-6]and superconducting quantum devices.[16,17]
Three concerns are experimentally related.(i) At a first glance,the relative stability of the bias fieldb0/B0is roughly 0.01%.Although such a highly stable magnetic field has been realized in recent experiments, where the bias magnetic field is of the order of~1 G and stabilized to a range from 10µG to 0.1 mG,[7,52,53]we note that the magnetic field stability is actually characterized by the stray magnetic field.Thus the ratiobc/B0is about 1%, which is quite easy to realize.(ii) The rapid reversion of the bias field (in the order of~1 µs) was achieved in experiments without introducing adiabatic Landau-Zener transitions between atoms in different spin components.[56]Therefore we may neglect the short reversion time of the bias field during our numerical simulations.(iii) To measure〈Jy〉 in a spin-1 BEC experiment, one may employ continuous measurement using magneto-optical imaging techniques,[55]or projective measurement using the Stern-Gerlach technique after an additionalπ/2 pulse which rotates the condensate spin tozdirection.[52]
For the purpose of a concise illustration of PRM, we have assumed several idealizations for the magnetic field sensitivities to reach the HL.Specifically, the sensitivity calculations do not take into account any dead time during statepreparation and measurement stage, and assume hard pulses with instantaneous and perfect rotation.Therefore, the sensitivities achieved in practical experiments are not as prominent as predicted here.Nevertheless,our results point out the possibility to suppress noises with DD for a DC magnetometer using PRM.It is worthwhile to design more robust pulse sequences accounting for pulse width and shape,in order to meet practical requirements.
Appendix A:Parameter estimation and sensitivity
Under the single mode approximation,[40]the Hamiltonian for the magnetometer based on atomic spin-1 Bose-Einstein condensate is given by

With the (to be estimated) signal magnetic fieldb0assumed static and pointed along thez-axis, the Hamiltonian in the absence of stray field reduces toH0=-c′2J2+γb0Jz.To estimateb0, a polarized initial stateψ(0), e.g., a coherent spin state (CSS) with its average spin alongx-direction taking the maximum collective spin value〈Jx〉=Jis prepared.It evolves underH0for an interrogation timetand becomesψ(t)=exp(-i[-c′2tJ2+φsJz])ψ(0), whereφs=γb0tis the accumulated dynamical phase from the signal fieldb0.One can determineb0by measuring a dependent observable, for instance,〈Jy〉, which gives〈Jy〉(t)=Jsin(φs).According to parameter estimation theory,the value ofb0can be estimated from the measured〈Jy〉(t)through the relation
The sensitivity for such a magnetometer is defined as

an optimal sensitivity that scales as 1/J,which is beyond SQL and approaches to the Heisenberg limit(HL).The scaling with respect toJmanifests the quantum enhancement to measurement precision by using SSS.
Appendix B:Free evolution in dephasing noises
To facilitate analytical derivation, we consider the dephasing model in which the stray field distributes uniformly within[-bc,bc]only alongz-direction.The system Hamiltonian becomesH=-c′2J2+γbzJz+γb0Jz, wherebzdenotes thez-component of the stray magnetic field.
It is easy to calculate straightforwardly the evolution of〈Jy〉 for an initial CSS with spin initially polarized alongxdirection,which follows

Acknowledgements
Project supported by the NSAF (Grant No.U1930201),the National Natural Science Foundation of China (Grant Nos.12274331, 91836101, and 91836302), the National Key R&D Program of China (Grant No.2018YFA0306504), and Innovation Program for Quantum Science and Technology(Grant No.2021ZD0302100).The numerical calculations in this paper have been partially done on the supercomputing system in the Supercomputing Center of Wuhan University.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry
