Three-dimensional magnetic reconnection in complex multiple X-point configurations in an ancient solar–lunar terrestrial system

Xiang-Lei He(何向磊), Ao-Hua Mao(毛傲华),2,†, Meng-Meng Sun(孙萌萌),Ji-Tong Zou(邹继同), and Xiao-Gang Wang(王晓钢),2

1School of Physics,Harbin Institute of Technology,Harbin 150001,China

2Laboratory for Space Environment and Materials Science,Harbin Institute of Technology,Harbin 150001,China

Keywords: magnetic reconnection,multiple X-points,complex magneto-plasma system

1.Introduction

Magnetic reconnection processes have been extensively observed and studies in space, astrophysical, and laboratory plasmas,particularly for explosive events such as solar flares,coronal mass ejections, magnetic storms and substorms, disruptive instabilities in toroidal fusion plasmas,etc.[1-6]An important development in magnetic reconnection studies is the fast reconnection dynamics in the collisionless regime[7-9]on a multiple scale as small as electron skin-depth.[10,11]On the other hand,progress is also made in the front of reconnection processes with complex field configurations,such as 2D multiple X-point reconnection models for space and laboratory plasmas,[12,13]and particularly 3D reconnection processes with multiple nulls and complex separatrix structures.[14-16]In fact, many celestial bodies[17-20]and galaxy clusters[21,22]in the universe have or ever had magnetic fields with various 3D configurations.Thus,for big planets(such as Jupiter and Saturn) with moons having remarkably durable magnetic fields,a typical 3D complex magnetic geometry can be formed in the moon-planet-IMF system.The energy/matters transport and evolution processes in such magnetic field configurations are essential to astrophysical research subjects.While magnetic reconnection physics around a single X-point has been extensively investigated and remarkable progress has been made,[1,23]however geometrical features and dynamical characteristics of 3D magneto-plasma systems with complex configurations are still open issues.

To our Earth-Moon-IMF system,although on the present lunar surface, only a negligible magnetic intensity of＜0.2 nT,[24]～10-5of that on the Earth, is detected, it is indicated that there had been a substantial lunar magnetic field billions of years(Ga)ago,by study of magnetized lunar rock samples.[25]It has been found that many Apollo samples carry significant remnant magnetization, indicating that the ancient lunar dynamos operating 4.25-2.5 billion years ago(Ga)had a substantial surface field of 5µT-100µT,comparable to that of today’s Earth.[25]Particularly,because the Earth-Moon distance～4 Ga ago is shorter than the present value of～21.6 Earth-radius (RE),[26]the interaction would be stronger than today’ value.Such Earth-Moon interactions were first studied in a model of parallel and antiparallel dipoles coupling in the Earth-Moon system,[27]where the ancient Moon was located 18REaway from the Earth.For simplification however,the IMF effect is reduced to a perfect paraboloid magnetopause surrounding the geomagnetosphere.The Earth-Moon fields then form various reconnection configurations in such a modeling geomagnetosphere to provide pathways between the Earth and the ancient Moon.

In this work, therefore, we develop the model into a 3D system open to the IMF environment of a typical moonplanet-IMF configuration to investigate complex geometry magnetic reconnection.The rest of this paper is organized as follows.The model and simulation setting are introduced and described in Section 2.Temporal evolutions of the Earth-Moon-IMF system in various IMF orientations,as well as features of magnetic reconnection for typical Earth-Moon relative positions, are revealed and analyzed in Section 3.The simulation mainly focus on representative reconnection processes of north or south IMF orientations with only brief descriptions for others.Then in Section 4, prospects and some conclusions are drawn and the prospects are also discussed.

2.Methods and simulation setups

The temporal evolution of the Earth-Moon magnetic field system in the IMF environment is modeled by a global 3D magnetohydrodynamics (MHD) model widely applied to space and astrophysical plasma physics, such as in coronal heating,[28]coronal mass ejection,[29]particularly geomagnetosphere-IMF coupling,[30-32]etc.A detailed description of the model and its numerical solver can be found in Ref.[33].Characteristic parameters,such as the Earth-Moon distance (DEM=18RE), fierce solar wind conditions due to the “faint young Sun”,[34]and especially ancient Earth field and Moon field～3 Ga-4 Ga ago[27]are selected in the simulation of this work.The magnetic field configurations are assumed to be generated by Earth-Moon dipoles,either parallel or anti-parallel in the north-south direction, in a steady IMF.And the respective intensities on Earth surface and Moon surface are approximately the same as～Bsurf=31.2µT,almost at a level on the present Earth surface.

Without loss of generality,the initial state can be assumed to be force-free with a constant pressurep=psw=nswTsw.The number density of the Earth’s geomagnetosphere plasma is however approximately inversely proportional to the fourth power of the geocentric radius as[35]

withr=(x2+y2+z2)1/2,n0=104cm-3andnsw=5 cm-3are the number densities of solar wind plasma and ionosphere plasma atr ≈RErespectively, withrbeing the geocentric radius.Clearly,ther-4distribution is extended only tora=6.67RE,slightly lower than the geostationary orbit,wherenE(ra)=nsw=5×10-4n0.Meanwhile,we choose the inner simulation boundary atr=rb=3RE, withnE(rb)≈10-2n0.It should be pointed out that at the Moon position ofr～18RE,the plasma densitynM≈0.1 cm-3≪nswis obviously submerged in the background solar wind densitynsw.Thus,under the force-free assumption for the initial distribution,the isothermal stateT=Tsw= const.can be used, except for a small region ofrb(=3RE)≤r ＜ra(=6.67RE) whereT(r)/Tsw= (nsw/n0)(r/RE)4, withT(ra) =Tsw,T(rb) =Tsw(rb/ra)4≈4×10-2Tsw.

withra=6.67,rb=3, andnsw=5×10-4(Tsw=4×10-4andpsw≈2×10-7).

The simulation domain is a 3D cubic box ofLx0≤x ≤Lx1,-Ly0≤y ≤Ly0,and-Lz0≤z ≤Lz0withLx0=-70,Lx1=30,Ly0=Lz0=50.And in general, the meridian plane ofy=0 is selected as a representative unless otherwise specified.The solar-wind/IMF flow into the domain through the boundary atx=Lx1.Thus, boundary conditions are adopted as a solarwind/IMF driving boundary atx=Lx1, free boundaries atx=Lx0,y=±Ly0, andz=±Lz0.Besides, fixed boundary conditions arer=3REas in Eq.(1), and 3 of lunar radius(RM)from the Moon center.

3.Results and discussion

Instead of two particular Moon positions at the noon and the midnight on the meridian plane in Ref.[27],in this work,we observe three typical local time(LT)positions of the Moon when it orbits the Earth, i.e., 0 LT(the midnight), 12 LT(the noon),and 6 LT(the dawn,symmetric to the dusk),as shown in Fig.1.Contributions at the 18 LT position (the dusk) are the same as that at the 6 LT.Also,the geocentric solar ecliptic(GSE)coordinates are adopted with the origin in the center of the Earth.

The initial magnetic field configuration in the meridian plane ofy=0 is exhibited in Fig.2.Taking the 0-LT case for example,the surface fields at the equator is assumed to beB0≡|BRE0|=|BRM0|,[27]whereBRE0is the surface field of the Earth andBRM0is that of the Moon.

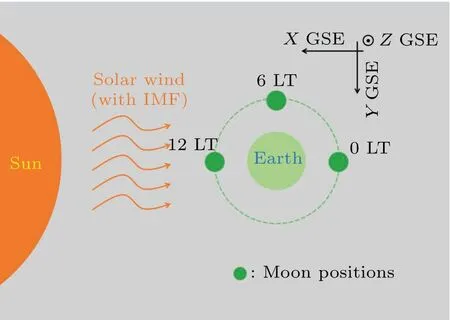
Fig.1.Schematic diagram of the three representative positions in the simulation.

We then exhibit simulation results for three typical Moon positions with various Earth-Moon dipole alignments and different IMF orientations.For both antiparallel and parallel dipoles, quasi-steady-state configurations of the Earth-Moon system are reached in the 3D simulation for three typical Moon positions.In each case,the influence of the IMF orientation is also investigated.We first discuss reconnection features for the Moon at 0-LT and 12-LT positions, which are corresponding to midnight and noon, respectively, because of the similarity to the 2D geometry due to the symmetry about the meridian plane ofy=0.The reconnection process for the Moon at the 6-LT position(case dawn)is investigated in a full 3D picture.The case for the Moon at the 18-LT position (case dusk) is similar to the case dawn due to the mirror symmetry.

By analyzing the characteristics of magnetic nulls and separatrices, major features of magnetic reconnection in the Earth-Moon-IMF system, such as the current sheet and inoutflow structures, can be acquired.The temporal evolution and plasma-magnetic configurations of the system are then investigated in detail for various dipole alignments,IMF orientations,and relative positions of the Earth and the Moon.

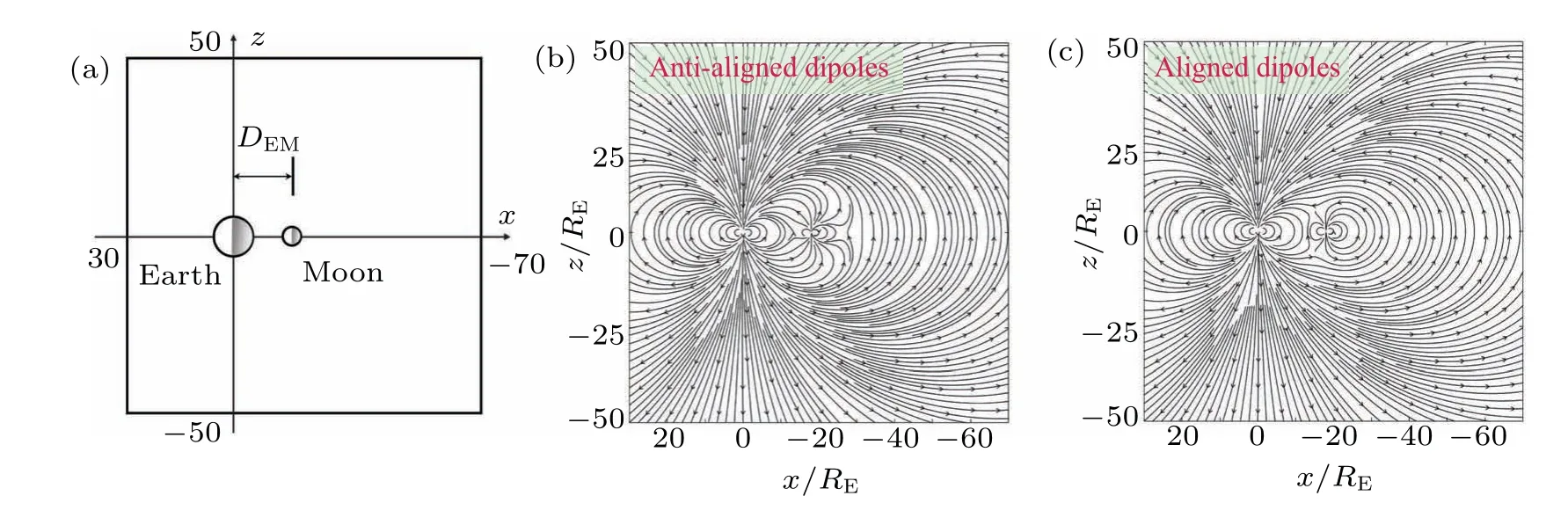
Fig.2.(a)Cross-section of meridian plane for 0-LT case,and initial magnetic field distribution for(b)antiparallel dipoles and(c)parallel dipoles.

3.1.Magnetic reconnection for the Moon at 0-LT position

In order to clearly show the characteristics of reconnection configurations and plasma, we mainly describe the process in a 2D approximation.

Magnetic reconnection in the 2D geometry has been extensively studied.[1,36,37]Clearly,in the case midnight,the 2D projection onto the meridian is always of a 2D X-point geometry.The 3D simulations show that there are three typical reconnection configurations in the Earth-Moon system:(i)the X-line structure,(ii)the triple current sheet structure,and(iii)the A-B null pair structure.Each reconnection geometry is investigated in detail at a quasi-steady-state(QSS)with certain typical examples.

Now, we take a specific case for example.In Fig.3,we plot QSS magnetospheric configurations on the meridian plane (y=0), with antiparallel Earth-Moon diploes being in the southward IMF at 0 LT.A typical magnetosphere with a parabolic shape is formed and clearly observed by the dayside compression in the nightside drag of the IMF.Clearly,positioning behind the Earth,the Moon cannot affect dayside reconnection at the geomagnetopause.For a southward IMF,dayside geomagnetopause reconnection occurs on the subsolar point(B1 marked in Fig.3(b)),in accordance with conventional observations as well as theoretical and numerical models without the lunar magnetic field.Nevertheless,in the geomagnetotail region,reconnection sites and features are totally changed.Instead of at the near-Earth or far neutral lines,with a significant lunar magnetic field, magnetic reconnection appears in more places between the Earth and the Moon,on the equatorial (z=0) plane (B2 marked in Fig.3(b)) and at the cusps of the Moon(B3 for the upper,marked in Fig.3(b)).

Then, we first investigate reconnection features at the equatorial plane site and show them in detail in Fig.4.It is found that by the reconnection currentJy(Fig.4(a)) and the plasma flowvdistribution(Fig.4(b))with the inflow component ofvx(Fig.4(c))and outflow component ofvz(Fig.4(d),the features are very similar to those in conventional geomagnetotail reconnection with no lunar field.

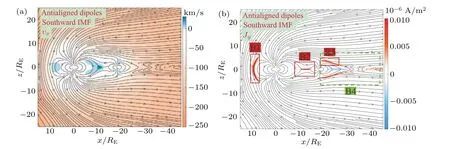
Fig.3.QSS reconnection configurations in case midnight, with antiparallel dipoles and southward IMFs.Magnetic field lines (in black)projection,as well as(a)x-component velocity vx and(b)y-component current density Jy (both by color bars)on the meridian plane.

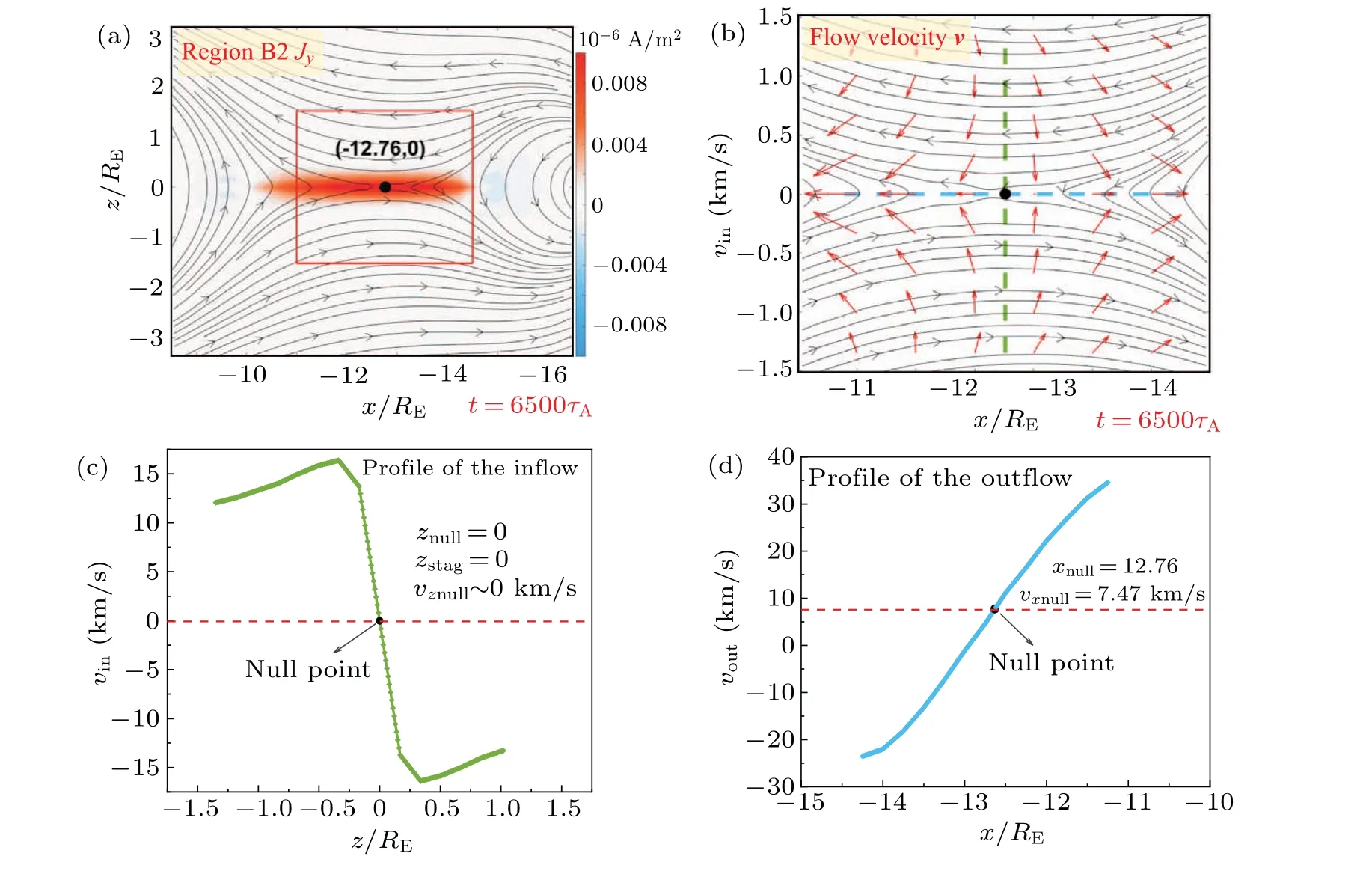
Fig.4.Locally enlarged region around B2 marked in Fig.3(c),for(a)reconnection current Jy and(b)plasma flow v distributions on equatorial(z=0)plane;also for velocity profiles of(c)inflow and(d)outflow,along green and blue dotted lines marked in panel(b).

It can be found that the X-point(in 2D case)on the equatorial (z=0) plane is located at (x,z)=(-12.76,0), marked by the red dot in Figs.4(a) and 4(b).A reconnection currentJycan be observed mostly distributed along thexdirection to support the magnetic reconnection process.And the plasma flow forms a typical inflow-outflow structure as shown by arrows on the meridian plane.The moonward outflow can bring most of materials from the Earth’s atmosphere to the Moon at a speed of～20 km/s, indicating that the reconnection has promotes the implantation of the lunar atmospheric proposed by Green.[27]Furthermore,one can calculate the reconnection rate by||Ey||≈1.63×10-6at the X-point, for estimating the magnetic flux transport.

On the other hand, instead of a reconnection site in the lunar magnetotail on the equatorial plane, the other two reconnection sites of case midnight with antiparallel dipoles and southward IMFs appear in lunar cusps as shown in Fig.5 for a local enlargement of the lunar magnetotail.

It can be seen that a triple current sheet configuration(ofJy)is formed with the+ydirection in two high latitude regions and the-ydirection near the equatorialz=0.Such a triple current sheet structure has been observed in coronal helmet streamers[38]and advance tokamak scenarios with reversed magnetic shear.[39]Here,however,the magnetic configuration with triple current sheets in the Earth-Moon system is different from the previous one, for the central current sheet with neither magnetic separatrix nor reconnection.In the lunar cusp region as shown in Fig.5(a),the closed lunar field lines are reconnected with the antiparallel magnetic field of the geomagnetosphere.Some newly reconnected field lines then turn to open and sweep tailward with the plasma flow,others however become connecting both the Earth and the Moon.As a consequence,the nightside closed lines of the lunar field are kinked by the separatrices (marked by red lines in Fig.5(b))of cusp region reconnection.A distant neutral line might be formed as the central current sheet extends over 90REor even farther away.It is however far beyond the simulation domain and with little influence on the magnetic flux transfer discussed in this work.

Unlike the antiparallel dipole geometry, reconnection in the parallel dipole geometry in case midnight occurs in the high latitude lunar cusp region, with no triple current sheet formed in the tail region.

Table 1.Antialigned dipoles at 0 LT.

Table 2.Aligned dipoles at 0 LT.

Thus, magnetic reconnection processes with various dipole alignments and IMF orientations in case midnight are simulated and summarized, and the results are listed in Table 1, and the results of aligned dipoles are listed in Table 2.Their contributions to magnetic flux transport are discussed later.

3.2.Magnetic reconnection for Moon at 12-LT position

In comparison with case midnight, for case noon with the Moon at 12 LT, the magnetospheric shape is much more complicated as shown in Fig.6.For the antiparallel dipoles,the magnetic reconnection site appears in the area between the Earth and the Moon (B2 marked in Fig.6(b)), the lunar cusp region (B1 marked in Fig.6(b)), and the geomagnetotail (B3 marked in Fig.6(b)).

Fig.6.QSS reconnection configurations in case noon,with antiparallel dipoles and southward IMFs.Magnetic field lines(in black)projection,as well as(a)x-component velocity vx and(b)y-component current density Jy (both by color bars),are shown on the meridian plane.

In this case, unlike the case midnight, 3D features of reconnection configurations in the dayside are more significant.We then focus on the null pairs as a specific example.As observed by the Cluster spacecraft,[40,41]the null pair can be connected by a separator of the intersection of separatrices(called fans orΣ-surfaces)bounded by spines(γ-lines).[42,43]Taking region B1 marked in Fig.6(b)for example,the null pair structure is exhibited in Fig.7 with the antiparallel dipoles and the southward IMF for case noon.As shown in Fig.7(a), a BA-B null structure is formed in the lunar cusp region with the nulls (all on the meridian plane,y= 0, due to the symmetry) connected by an intersection (marked by a purple line in Fig.7(b))of their fans.The fan of the A-type null(the green dot) is in green and that of the right B-type null (the orange dot) in Fig.7(a) is in orange as shown in Fig.7(b).Topologically, the fansΣAandΣBare bounded by the spinesγBandγArespectively.And the structure connecting the left Bnull and the A-null shows a similar structure.We then adoptE‖=E·B/|B|2～10-19at the midpoint of the separator to estimate the reconnection rate,which is nevertheless found to be much slower than that inX-line reconnection at subsolar point in case midnight.2

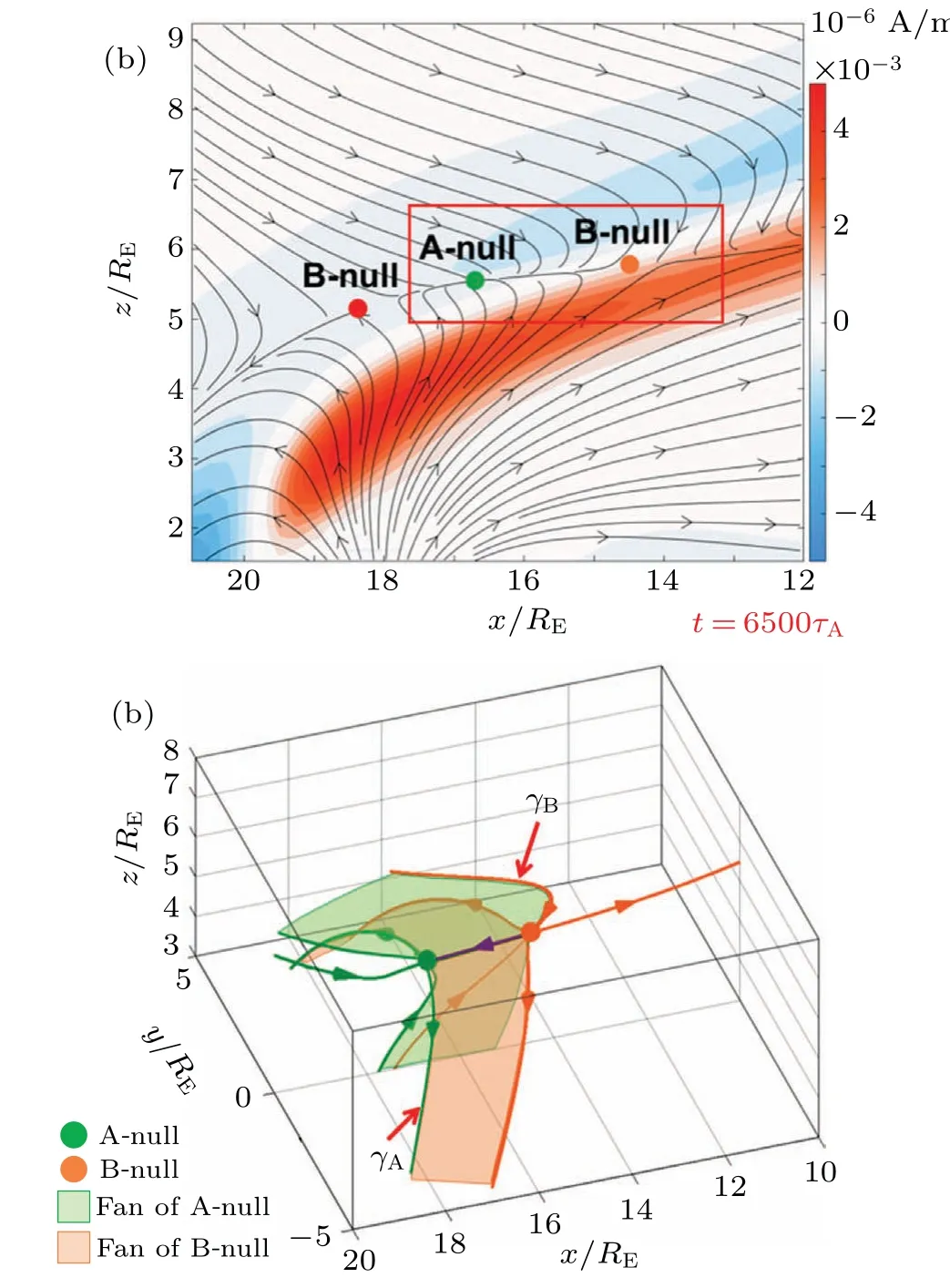
Fig.7.(a)Local enlargement of Region B1 marked in Fig.6(b);(b)3D structure of A-B null pair inside red box in panel(a)and its fan.

Reconnection in the area between the Earth and the Moon,for case noon,is greatly influenced by the IMF orientation.For example,the reconnection(B2 marked in Fig.6(b))inflow, for the southward IMF, is almost in thexdirection,while for the northward IMF, the reconnection inflow is almost in thezdirection, similar to that in case midnight with both southward IMF and northward IMF.And for case noon with the parallel dipoles,reconnection occurs at lunar magnetopause,lunar cusp regions,Earth’s cusp regions,or geomagnetotail according to various IMF orientations.Moreover,for the southward IMF, reconnection in the Earth’s cusp region leads to an increase of the closed lunar magnetic flux while it has no influence on the lunar flux when the IMF orientation is northward.Besides, reconnection appears in the geomagnetotail for case noon with various dipole alignments and IMF orientations,similar to conventional geomagnetotail reconnection for today’s geomagnetosphere, without the triple current sheets configuration.

We then summarize the reconnection processes and their features at different sites for case noon, with various dipole alignments and IMF orientations,in Tables 3 and 4.

Table 3.Antialigned dipoles at 12 LT.

Table 4.Aligned dipoles at 12 LT.

3.3.Magnetic reconnection for Moon at 6-LT and 18-LT positions

Furthermore, the case for the Moon at the dawn side of the Earth at the 6-LT position(case dawn)is also investigated,while the case for the Moon positioning at the dusk side of the Earth(18 LT,case dusk)is symmetric to the former.

No or negligible reconnection is detected on the dawn side and dusk side of the Moon for case noon and case midnight.However, in case dawn/dusk, reconnection occurs not only at the magnetopause, magnetotail, and cusp regions of the Moon, but also notably on lunar dusk and dawn sides.The distributions ofx-component current,Jx, on the dawndusk(x=0)plane with different IMF orientations are shown in Fig.8.For the southward IMF (Fig.8(a)), a current sheet flowing along thexdirection can be clearly observed between the Earth and the Moon(region A1),indicating magnetic flux transferring to the Moon by reconnection on the current sheet.And in the vicinity of the Moon, the high latitude current sheets symmetric about the equatorial (z=0) plane can generate reconnection in the lunar cusp region.For the northward IMF (Fig.8(b)), reconnection occurs at the dusk (region B1)side and the dawn(region B2)side of the Moon.The duskside(between the Earth and the Moon)reconnection rate is greatly weakened due to antialignment of the dipoles,while the dawnside reconnection rate is on the same order of magnitude as that of conventional X-line reconnection.

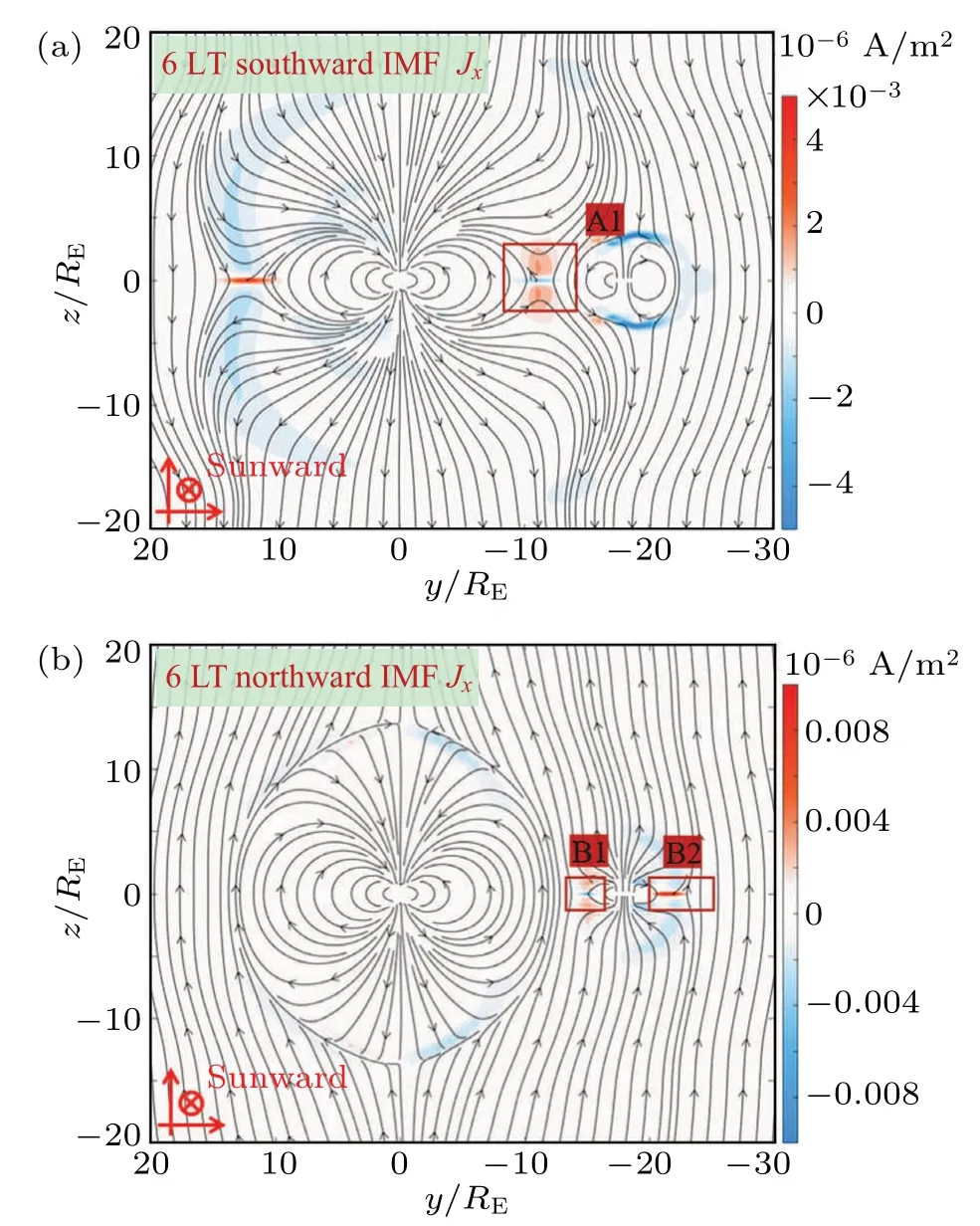
Fig.8.QSS magnetic configurations with antiparallel dipoles at dawndusk cross-section x=0.Patterns of magnetic field lines(in black)and x-component current Jx (denoted by color bar)are shown for(a)southward IMF and(b)northward IMF.

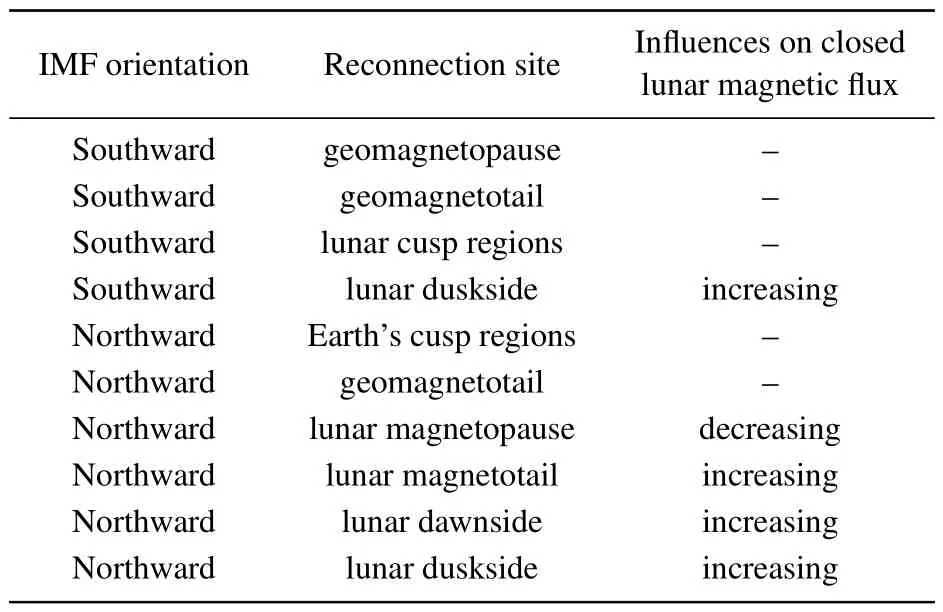
Table 5.Antialigned dipoles at 6 LT.

Table 6.Aligned dipoles at 6 LT.

Besides,around the Earth in case dawn/dusk,the feature of reconnection on the meridian (y=0) plane is very similar to that in conventional reconnection in today’s geomagnetosphere.Nevertheless,such a kind of reconnection has almost no influence on the lunar flux transfer concerned.

Features of reconnection processes at various typical sites and their contributions to magnetic flux transports are then summarized in Tables 5 and 6.Due to the mirror symmetry,the contributions in case dusk are similar to those in case dawn.

4.Conclusions and perspectives

As a complex 3D system, the ancient solar-lunar terrestrial magneto-plasma system existing in the epoch when the Moon still possessed a global magnetic field substantially differs from the present-day geomagnetosphere.Specifically,the 3D magnetic reconnection process,magnetic configuration evolution of the ancient Earth-Moon-IMF system and corresponding reconnection dynamics are studied in a 3D MHD model with the various alignments of Earth-Moon dipoles and IMF orientations.The coupled quasi-steady-state magnetospheres are formed under different IMF conditions corresponding to various multiple X-points at various locations,including the geomagnetopause, the Earth’s cusp region, the geomagnetotail, the lunar magnetopause, the lunar cusp region, the lunar magnetotail, and the area between the Earth and the Moon.Such geometries and processes can provide an effective pathway for facilitating the Earth-to-Moon transport of energy and materials, creating a possible mechanism and holding significant importance in understanding the origin and the evolution of the atmospheric and the soil constituents for coupled astrophysical systems with similar transport process.

Based on our research,there are three typical magnetic reconnection structures found in the simulation, i.e.the X-line,the triple current sheets,and the A-B null pair structures.The X-line structure occurs mostly in the area between the Earth and the Moon and the geomagnetopause with the southward IMF.The meridian cross-section of the X-line structure is a typical X-point geometry with a clearly inflow-outflow configuration.The A-B null pair structure appearing mainly at the lunar cusp region is more stable with a much lower reconnection rate than that for the X-line.The A-null and the B-null are linked by a separator line as an intersection of the fans(Σsurfaces).Besides, a larger spatial scale magnetic reconnection structure is formed in the lunar magnetotail at 0 LT when the dipoles are antiparallel, with a triple current geometry of two reconnection currents along the+ydirection at the lunar cusp and the other aligning tail current in the-ydirection.Furthermore, for case dawn/dusk, reconnection on the lunar dusk side and dawn side may be significantly strengthened,thereby making a great influence on the closed lunar flux.The results of the complex multiple X-point configurations demonstrate a fresh and critical reconnection topology for 3D asymmetric system.With such a topology, the magnetic field line configuration and the magnetic flux transfer process are different from the present-day Earth,offering a valuable idea for comprehending other asymmetrical coupled systems.

Therefore, based on our 3D MHD simulations, it can be proposed that magnetic reconnection may have a great influence on coupling and evolution of Moon-planet-IMF system and play a substantial role in their magnetic environments.For such astrophysical systems, the coupled magnetosphere can protect their ionospheres and atmospheres from eroding by high-energy particles and solar wind, resulting in a habitable environment that can lead to life.And on the other hand, as a key mechanism of the significant energy transfer process such as magnetosphere storms and substorms,the magnetic reconnection exhibits an intricate spatial configurations and temporal dynamics, potentially intensifying the extreme space weather events.For example,in the solar system,Jupiter,Saturn,and their major moons exhibit global magnetic fields,[44-46]indicating the possibility of analogously coupled magnetospheres and reconnection processes.Consequently,due to the existence of multiple X-point structures,some fastgrowing events on these planets may show increasing complexity.Our work may also be of potential relevance in guiding the search for exoplanet life and the exploration of planets in the solar system.Further investigations for other dipole alignments and IMF orientations, as well as complex 3D reconnection geometries are subjects of future studies.

Acknowledgements

The authors thank Z.W.Ma and his team in the Institute for Fusion Theory and Simulation,Department of Physics,Zhejiang University,for providing the original 3D MHD code.

Project supported by the National Natural Science Foundation of China (Grant Nos.11975087, 42261134533, and 42011530086), the National Magnetic Confinement Fusion Energy Research and Development Program of China (Grant No.2022YFE03190400), and the Heilongjiang Touyan Innovation Team Program,China.