Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

Xiaoxia Li(李晓霞), Qianqian He(何倩倩), Tianyi Yu(余天意),Zhuang Cai(才壮), and Guizhi Xu(徐桂芝)

1Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province,Hebei University of Technology,Tianjin 300130,China

2State Key Laboratory of Reliability and Intelligence of Electrical Equipment,Hebei University of Technology,Tianjin 300130,China

3School of Life Science&Health Engineering,Hebei University of Technology,Tianjin 300130,China

Keywords: hyperbolic-type memristor,Hopfield neural network(HNN),asymmetric attractors,image encryption

1.Introduction

The nervous system, comprising a vast network of interconnected neurons,[1,2]is one of the most complex systems in the human body.Neurons communicate and transmit electrochemical signals to accomplish various physiological functions,including perception,cognition,and motor control.Numerous physical and biological experiments have demonstrated a wide range of dynamic phenomena associated with neural activity within the nervous system.[3,4]For instance,several neurological disorders,such as epilepsy,[5]psychiatric diseases,[6]and Alzheimer’s disease,[7]have been found to correlate with the dynamics of the nervous system.[8,9]Hence,it is crucial to study chaotic dynamics in neural networks to better understand and address neurological diseases.Various neural network models[10-14]have been developed to explore and replicate the dynamic activities of biological neural systems.The Hopfield neural network(HNN)[15]is a widely employed computational model of the neural system.It not only captures the intricate connectivity patterns of the brain’s neural network but also possesses the ability to reproduce complex electrical discharge behaviors observed in the brain.In recent years, several improved HNN models have been proposed,such as the synaptic-coupled HNN,[16]fractional-order HNN,[17]hidden chaotic HNN,[18]and multi-winding memristor HNN.[19,20]

The memristor[21]is an electronic device capable of emulating the synaptic plasticity observed in biological synapses,making it suitable for constructing various types of neural network models.Memristor-based neural network models can be classified into two categories: electromagnetic radiation neural network models[22,23]and memristive synaptic neural network models.[24,25]Among them, the electromagnetic radiation neural network model is a particular type of model that utilizes flux-controlled memristors to establish the correlation between magnetic field strength and membrane voltage in neural networks.The dynamic behaviors of neurons or neural networks are investigated in this model,focusing on the impact of external stimuli, including electromagnetic radiation and electric field stimulation.The former influences the electrical activity of neurons[26,27]while the latter can induce mode transitions in isolated neuron electrical activity.[28]In their ground-breaking work,Liet al.[29]were the pioneers in uncovering that electromagnetic radiation has the capability to suppress the electrical activity of neurons and regulate the collective dynamics of neural networks by employing the Hodgkin-Huxley neuron model.Wanet al.[30]utilized hyperbolic-type and quadratic nonlinear memristors to simulate the effects of electromagnetic perturbations and radiation on a hypernetwork neural network.Their research uncovered intricate dynamic behaviors displayed by the HNN across different coupling strengths,confirming the presence of bistable patterns.The memristive synaptic neural network model establishes connections between neurons and facilitates information transmission by leveraging the synaptic properties of memristors.Linet al.[31]demonstrated complex behaviors of spatial multistructures and spatial initial offset in a memristive Hopfield neural network (mHNN) with three memristor coupling weights.Maet al.[32]developed a multi-stable HNN incorporating two generalized memristor synapses.Indeed,the findings of their study provided evidence that the modified mHNN with dual memristor synapses displays chaotic behavior and coexists with asymmetric attractors.These two models have higher dynamism and complexity than the original neural network model and can produce various phenomena such as attractors, periodicity, chaos, chimera states,[33]and offset enhancement.[34]Currently,research on memristor synapse neural network models is still in the early stages and requires further theoretical studies and experimental validation to uncover their mechanisms and advantages.

Chaotic signals, characterized by internal randomness and deterministic properties, can be utilized for generating pseudo-random numbers[35,36]and are of great importance in the fields of image watermarking[40]and image encryption.[39,41]In the field of artificial intelligence, including machine learning, image encryption, and information security, researchers have shown a growing interest in the application of HNNs.Particularly,the generated chaotic signals from HNNs have garnered significant attention among professional researchers in the realm of image encryption.Numerous studies have indicated that image encryption techniques utilizing HNNs characterized by intricate chaotic dynamics showcase exceptional performance in terms of encryption.By employing HNNs with chaotic dynamics to generate scattering matrices, several encryption algorithms for color images have been suggested.[40-42]Yuet al.[43]presented a novel image encryption algorithm that utilizes a multiscroll mHNN for achieving secure encipherment.Currently,researchers are actively involved in the advancement of contemporary encryption techniques for sensitive data,including applications such as encrypting medical images[44]and ensuring privacy protection for medical data.[45]Because of their intricate dynamic characteristics, these encryption techniques demonstrate enhanced security efficacy in contrast to earlier schemes.Hence,the development of chaotic systems utilizing mHNNs has emerged as a prominent research area, gaining substantial attention in scientific and technological domains.

Based on the preceding discourse, this study explored the tumultuous dynamics of non-symmetrical hyperbolic-type memristors and their utilization in image encryption.This study presents the following key innovations and advancements:

(1)A new and simple hyperbolic-type three-dimensional mHNN model is proposed to explain its chaotic mechanism.

(2) Nonlinear analysis tools are used to show that compared with previous models, the introduced hyperbolic-type mHNN exhibits a coexisting bistability of chaotic attractors and periodic attractors, which is verified through Multisim simulation.

(3) Based on the hyperbolic-type mHNN, an image encryption scheme is introduced by examining the color channels (red, green, and blue) of the image.The proposed encryption scheme exhibits reduced correlation,increased information entropy,and good resistance to differential attacks and resistance robustness.

The subsequent sections of this paper are organized as follows.Section 2 provides an introduction to a hyperbolic-type mHNN model,emphasizing its bounded behavior and analyzing the stability of equilibrium points.In Section 3,traditional analysis tools are employed to investigate the coexistence and bistability phenomenon of asymmetric attractors.Section 4 presents an image encryption scheme built upon the mHNN.Section 5 outlines the design of a simulation electronic circuit to validate the system’s feasibility.Lastly,Section 6 provides a summary of the paper.

2.Hyperbolic-type memristor emulator

2.1.Math model

A memristor is a type of nonlinear resistor with memory,nanoscale structure, low power consumption, and adjustable resistance.Therefore, memristors have wide applications in simulating neurons and synapses.Two categories of memristors exist: charge-controlled and magnetic-controlled.In neural networks,the activation function for neurons often employs the hyperbolic tangent function, which is a differentiable and monotonically bounded function within the range of-1 to 1.This paper uses a hyperbolic tangent-type memristor to simulate neuron synapses,and its model is given by

The input voltage and current of the memristor emulator are represented byvandi,respectively.The internal state variable is denoted asv0.The memductance of the magnetic-controlled memristor is given byW(v0)=a-btanh(v0),whereaandbare positive real coefficients.To facilitate calculations,ais set to 1,andbis a tunable parameter,which represents the memristor’s conductance in the magnetic-controlled memristor.

A system of circuit state equations is used to describe the HNN, which corresponds tonneurons.[46]The circuit state equation for thei-th neuron incorporates the use of a tangenttype memristor to simulate neuron synapses.The model for this equation is provided as follows:

The neuron cell membrane is characterized by its capacitance(Ci)and resistance(Ri).The voltage state variable across capacitorCiis denoted asxi, while the hyperbolic tangent activation function(tanh(xi))captures the neuron’s behavior.The synaptic weight matrix(W=(wi j)),with dimensions ofn×n,represents the connection strength between neuroniand neuronj.The input bias current is denoted asIi.It is important to note that the dynamic behavior of the mHNN is highly influenced by its synaptic weight values, and investigating the dynamics of a neural network with varying synaptic weights is both valuable and significant.

Fig.1.Topology of hyperbolic mHNN connections.

In this study,we examine a neural network with three neurons as illustrated in Fig.1.The connection matrix associated with this specific connectivity structure is given by

LettingCi=1,Ri=1,n=3, andIi=0, we can obtain the dimensionless equation that characterizes the behavior of the memristive network as follows:

whereW=a-btanh(x4) represents the nonlinear synaptic weight of the model.The constantkdenotes a positive value that characterizes the strength of coupling attributed to memristors with hyperbolic characteristics.Additionally,W32is an adjustable weight parameter.From this nonlinear relationship, it can be observed that the synaptic weight associated with the second neuron is influenced by the intrinsic value of the three neurons.This configuration can make the dynamics of the brain more complex.Equation (4) models the hyperbolic mHNN as a three-dimensional autonomous nonlinear dynamical system,capturing the nonlinear synaptic weight of the model.

2.2.Bounded proof

The parametersaandbin Eq.(4)are positive real numbers that relate to the hyperbolic-type memristorW32,and both of them are positive real numbers.It can be proven that the period and chaotic trajectories obtained from Eq.(4)are both constrained within a bounded region.

Based on the method described in Ref.[47],a Lyapunov function is presented as

For all (x1,x2,x3,x4) in a sufficiently large regionD0＞0,whereV(x1,x2,x3,x4)=DandD ＞D0,the following inequality holds:

is a bounded region encompassing all solutions of Eq.(4),i.e.,the proposed mHNN.

2.3.Equilibrium points and stabilities

The memristive model, Eq.(4), exhibits symmetry with respect to the parameterb,as indicated by the transformation of(x1,x2,x3,x4,b)to(-x1,-x2,-x3,-x4,-b).

To determine the equilibrium points of the mHNN system with hyperbolic memory resistance,one can solve Eq.(4)numerically while satisfying the condition that the left-hand side is zero andW32is fixed at 3.8.The equilibrium points of the system include one point at the origin,P0=(0,0,0,0),as well as two non-zero points,P1=(η1,η2,η3,η4)andP2=(µ1,µ2,µ3,µ4).These non-zero equilibrium points can be obtained by solving the following system of equations:

Analyzing the graphical intersection of the two function curves allows us to derive the values ofy1,z1,y2, andz2.For instance, considering the valuesk=0.3,a=1, andb=0.1,we can plot the two function curves described in Eq.(18) in Fig.2,facilitating the identification of their intersection points.By examining the graph, we obtain the solutions as follows:y1=0.0064,z1=1.8445,y2=-0.0199, andz2=-1.9390.From Eq.(18), we can easily solve for two non-zero equilibrium points,denoted asP1andP2.

Fig.2.The two function curves intersect at certain points when a=1,b=0.1,and k=0.3.

Equation (4) is used to derive the Jacobian matrix at the equilibrium pointP=(x1,x2,x3,x4)The eigenvalues ofP0are solely determined by the memristor’s internal parameteraand not influenced by the internal parameterb.According to the stability criterion established by Routh-Hurwitz,for a cubic polynomial in the form ofλ3+a1λ2+a2λ+a3=0, the parameters of the equation should satisfy the conditionsa1＞0,a3＞0,anda1a2＞a3in order for the solution to be stable.It can be seen that parameteracannot satisfy the conditiona1＞0 for Eq.(19),hence,the equilibrium point’s trajectory always exhibits instability.Hence, under this condition, system (4) cannot produce hidden attractors according to its definition.

The eigenvalues for the non-zero equilibrium pointsP1=(η1,η2,η3,η4) andP2= (µ1,µ2,µ3,µ4) can be determined through numerical simulations using MATLAB.Under the conditions ofa=1 andb=0.1,based on Table 1,variations in the internal memristor parameterklead to changes in the zero equilibrium pointP0,as well as the equilibrium pointsP1andP2.Furthermore,the alterations in the internal memristor parameterkalso have an impact on the corresponding eigenvalues and the type of chaotic attractors generated.This indicates that there exist multiple unstable equilibrium points in system (4) under different conditions of the internal memory resistance parameterk, suggesting that the system is capable of generating chaotic attractors and prone to exhibiting multistable phenomena related to the initial state.

Table 1.Equilibria points,eigenvalues,and types of equilibria.

3.Complex behaviors of the hyperbolic-type mHNN

The objective of this section is to investigate the diverse dynamics observed in the hyperbolic mHNN through the utilization of various analytical tools such as bifurcation plots,two-parameter maximal Lyapunov exponent graphs, phase plane orbits, Lyapunov exponents, and attraction basins.The dynamic behaviors of the 3D mHNN model, as described by Eq.(4), were numerically simulated using the fourth-order Runge-Kutta method.The Wolf method was employed to compute the Lyapunov exponent and evaluate the system’s sensitivity to its initial state.The simulations used a time step of 1×10-3to ensure accurate representation of the dynamics.

3.1.Parameter-dependent dynamic distribution

Witha= 1 and the initial condition set to (0.1, 0, 0,0), the comprehensive dynamics of the coupling parameters were explored through the utilization of two-parameter maximum Lyapunov exponent maps.Figure 3 displays these maps for the (k,W32) and (k,b) parameter combinations, providing an insight into the global behavior.When the memristive coupling parameterkand the synaptic weightW32change simultaneously, the color-coded map of the maximum Lyapunov exponent at each iteration is obtained and shown in Fig.3(a).The dynamics of the system, such as periodic attractors,quasi-periodic,and chaotic behavior,are recorded in these two-parameter Lyapunov exponent maps.The numerical value of the maximum Lyapunov exponent is indicated by different colors in the color bar, where periodic behavior with regular attractors is characterized by one color, quasiperiodic behavior is supported by another color, and chaotic behavior with bounded random patterns is supported by yet another color.Figure 3(b)shows the two-parameter maximum Lyapunov exponent map on thek-bplane.The complex dynamics are shown to evolve on thek-W32andk-bplanes in Fig.3,capturing the transition from the region of periodic behavior to that of chaotic behavior.

Fig.3.Two-parameters maximal Lyapunov exponent graphs.

3.2.Dynamics with coexisting bifurcation modes

When the model is initialized with the initial conditions of(0.1,0,0,0)and(-0.1,0,0,0),the bifurcation parameters chosen include the memristive coupling strengthk, synaptic weightW32,and initial statex3(0).

From the dynamic map of the parameter space in Fig.3,it can be seen that when the synaptic weightW32=3.8, the model(4) is in a chaotic state.Figure 4 displays the bifurcation diagram and Lyapunov exponent plot of the state variablex2.The plots were generated using the Runge-Kutta algorithm and Wolf algorithm,with fixed memristor internal coupling parametersa=1 andb=0.1.Figure 4(a)illustrates the bifurcation diagram and Lyapunov exponent spectrum of the model under two different initial conditions.The blue spectral line corresponds to the initial condition (0.1, 0, 0, 0), while the red spectral line represents the bifurcation diagram behavior under the initial condition (-0.1, 0, 0, 0).Similarly,in Fig.5(a), the teal spectral line corresponds to the bifurcation diagram and Lyapunov exponent spectrum under the initial condition (0.1, 0, 0, 0), while the green spectral line represents the bifurcation diagram behavior under the initial condition (-0.1, 0, 0, 0).Figure 4 shows that a coexisting asymmetric bistable mode is globally present in model (4).Figure 4 reveals various complex dynamic effects associated with the memristive coupling strength in model (4), such as the presence of coexisting periodic attractors,coexisting spiral chaotic attractors, forward period doubling bifurcations, and chaotic crises.By examining the bifurcation diagram, it becomes evident that the blue and red trajectories coincide within the ranges ofk=[0,0.08] and [0.1, 0.32], suggesting the absence of coexisting phenomena.Askprogressively increases within the range ofk=[-0.1,0.6], the dynamic behavior of model(4)undergoes a transition from a periodic limit cycle to a chaotic state,facilitated by a chaotic crisis.Whenk=0.09,the system transitions from the chaotic state to an unstable coexisting periodic attractor, which then enters a chaotic state.Coexisting bifurcations appear whenk=0.32, manifested as a single vortex chaotic attractor pattern.Whenktakes on values of 0.33 and 0.4155, the red and blue trajectories sequentially converge to a period-1 limit cycle through forward period doubling bifurcations from the chaotic state.The dynamics reflected by the finite-time Lyapunov exponent spectrum in Fig.4(b)align with those exhibited in the bifurcation diagram depicted in Fig.4(a).

Fig.5.With increase in memristor coupling strength W32,different initial conditions exhibit various bifurcation behaviors: (a)bifurcation diagrams of the state variable x2;(b)Lyapunov exponents.

Fig.6.The coexisting bifurcation behavior varies depending on the initial conditions of x3(0):(a)bifurcation diagrams of the state variable x2;(b)Lyapunov exponents.

Whenk= 0.2 and the internal coupling parameters of the two memristors are held constant ata=1 andb=0.1,Figs.5(a) and 5(b) illustrate the bifurcation diagram and the first three Lyapunov exponent spectra of the model under two sets of initial conditions,while the synaptic weightW32ranges from 2 to 12.The numerical results show that asW32varies in the range of[2,12],the mHNN model undergoes complex dynamic evolution.With increasing synaptic weightW32, the trajectory initiates from a period-1 limit cycle to an unstable chaotic state atW32=2.581,during which there is no coexisting phenomenon in the mHNN model.WhenW32=5.667,a coexisting chaotic state appears,and then the green trajectory undergoes reverse period doubling bifurcation atW32=6.646,degenerating into a period-4 limit cycle before entering a period-2 limit cycle.The teal and blue trajectories experience reverse period doubling bifurcations atW32=8.563, transitioning from a period-1 limit cycle to a period-3 limit cycle before ultimately reaching a period-2 limit cycle.

Withkfixed at 0.35 andW32at 3.8,the coexisting bifurcation behaviors of model(4)are examined based on initial conditions.The initial values of the two memristorsx2=x4=0 remain unchanged, whilex1is set to±0.1, andx3(0) serves as the bifurcation parameter.This is exemplified in Fig.6(a),where the black and purple trajectories correspond to initial conditions (0.1, 0,x3(0), 0) and (-0.1, 0,x3(0), 0) respectively.As the initial value of memristorx3(0) increases from-20 to 20, model (4) shows coexisting dynamic behavior of chaotic states and period-3 attractors alternatingly appearing.The results presented in Fig.6 indicate that model(4)exhibits a bistable mode induced by initial conditions.

3.3.Coexistence of attractors and bistability

Referring to the bifurcation diagram in Fig.4, multiple coexisting windows with different attractors can be identified.Taking the memristive synaptic weightk=0.32 as an example, a pair of coexisting chaotic attractors are displayed in Fig.7(a),and the corresponding basin of attraction.Atk=0.4,Fig.7(b)demonstrates the simultaneous presence of a period-2 attractor and a chaotic attractor.Atk=0.5,Fig.7(c)exhibits the coexistence of two distinct asymmetric attractors and a periodic attractor.Therefore,the phase portraits are different under different memristive coupling strengths,and the numerical results indicate that the memristive coupling strength can induce complex dynamical effects in the mHNN model.

Fig.7.Phase portraits of chaotic attractors in x1-x3 and corresponding basins of attraction at different k values: (a)k=0.32;(b)k=0.4;(c)k=0.5.

Fig.8.Basins of attraction on two different initial value planes: (a) basins of attraction on the initial value plane of x1(0)-x3(0); (b) phase portraits on the x1(0)-x3(0)plane.

In order to gain a deeper understanding of the model’s behavior and the impact of initial conditions, the attractor domains are characterized in various dynamical states using basins of attraction on the initial value plane.Figure 8(a)illustrates the basins of attraction on thex1(0)-x3(0) initial value plane,taking the Fig.6 bifurcation diagram as an example.In this case, withx2(0)=x4(0)fixed at 0, the green and yellow regions indicate the presence of periodic and chaotic attractors,respectively.Notably,the distribution of regions for each color is independent.Therefore, the phase portraits for two typical initial conditions, (3, 0, 3, 0) and (-3, 0, 3, 0), are shown in Fig.8(b),where a coexistence of chaotic and period-2 attractors is displayed,indicating that the model(4)exhibits bistable modes.

4.Image encryption

In order to investigate the application of mHNN,a novel color image encryption scheme was developed by leveraging the chaotic attractors generated by the mHNN.The encryption method employed in this scheme was thoroughly analyzed,and the resulting test results were carefully examined to assess its performance and effectiveness.The encryption process,as illustrated in Fig.9,follows the following steps.

Fig.9.Image encryption process.

Step 1 The settings area=1,b=0.1,k=0.35 and initial conditions are(0.1,0,0,0),with a time step 0.0005 and a discard number ofN=1000.The newly proposed mHNN neural network system was continuously iterated to generate chaotic sequences(x1(i),x2(i),x3(i),x4(i),r1,r2),where(x1(i),x2(i),x3(i),x4(i))are the initial conditions for this model,andr1,r2are two random 8-bit numbers.

Step 2 The original color picturePis divided into three parts:Pr,Pg,andPb.Chaos matricesS1,S2,S3,andS4are generated with a matrix size ofm×n.Scrambling and diffusion operations are then performed onS1,S2,S3, andS4.In this paper,two different formulas for diffusion and scrambling are used in image encryption.

The scrambling operation is a commonly used encryption method,which obfuscates the spatial structure of the image by changing the position,order,or exchange pixels of the pixels,making the encrypted image difficult to be decrypted.TakingS1as an example,with its messing method is as follows:

where the floor(x) function rounds the elements ofxto the nearest integer less than or equal tox.In this context,mandnrepresent the number of rows and columns in matrixP,while rows and cols correspond to the dimensions of matrixS1.The notationS1(i,j)refers to the element located at the intersection of rowiand columnjin matrixS1.Through the scrambling operation,each elementP(i,j)in the matrixPcan be mapped to a new position(u1,v1),globally scrambledPr,Pg,andPbto the following three sequences:

The diffusion operation aims to propagate the alteration of pixel values throughout the entire image, ensuring that each pixel is influenced by neighboring pixels.This process enhances the encryption strength, making it challenging to decrypt the encrypted image.We use the input matrixPand the chaotic sequenceSto calculate the output matrixC, and calculate the matrixTiof each row.The specific operation mode is as follows:

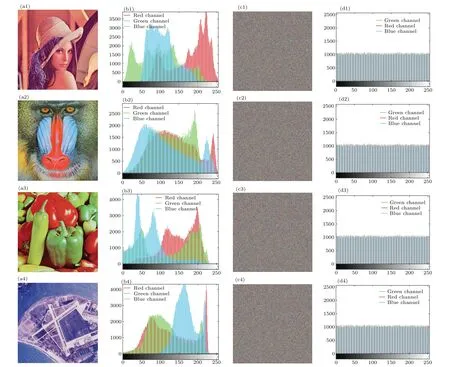
Fig.10.The image encryption results are presented as follows: (a1)-(a4)original images;(b1)-(b4)histograms of the original images;(c1)-(c4)encrypted images;(d1)-(d4)histograms of the encrypted images.

Step 3 Image decryption is the reverse process of encryption.

To showcase the effectiveness of the devised image encryption scheme, four representative images were chosen.These images include the Lena color image and three other color images (4.2.03, 4.2.07, and 2.1.05) sourced from the USC-SIPI data set.The selected images respectively represent human figures,animals,food,and remote sensing scenes,as illustrated in Figs.10(a1)-10(a4).These images possess varied content and share a common resolution of 512×512 pixels.Following encryption, the information becomes entirely concealed,rendering it visually impossible to discern the original image details.

4.1.Histograms

Histogram analysis is employed to assess the effectiveness of image encryption algorithms,illustrating the distribution of various pixel intensity values within the image.This necessitates achieving an even distribution of pixels with distinct intensities in the histogram,thereby bolstering resilience against statistical attacks.The assessment of the encryption system’s resistance to statistical attacks can be made by comparing the histograms of the original and encrypted images.Figure 10 presents the original color image and its corresponding encrypted image after being converted into three RGB channels.Additionally, the histograms of both images are displayed for comparison and analysis.Histogram analysis demonstrated a substantial enhancement in the uniformity of the encrypted image’s histogram in comparison to the original image.This observation suggests that the encryption system exhibits robustness against statistical attacks.

4.2.Correlation coefficient and entropy analysis

Analysis of the correlation between adjacent pixels evaluates the level of correlation between neighboring pixel values within an image.Typically,the original image exhibits a high correlation coefficient, approaching 1.To augment the confidentiality of the encryption algorithm in encrypted images, it is preferable for the correlation coefficient between adjacent pixels to approach zero in all three directions.This signifies the absence of significant correlation and strengthens the level of confidentiality.

Correlation analysis serves as a technique for assessing the confidentiality performance of encryption algorithms.A correlation coefficient approaching zero between adjacent pixels in the encrypted image signifies the encryption algorithm’s effective disruption of pixel correlation.Consequently,this enhances the confidentiality performance of the encryption system.The correlation between pixel pairs can be calculated using the formula provided below:

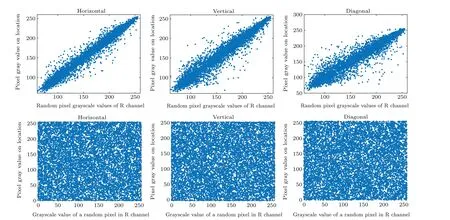
Fig.11.The correlation between the red(R)component of the plain Lena image and its corresponding cipher was analyzed in the horizontal,vertical,and diagonal directions.

Table 2.Correlation coefficients and information entropy values of the original and encrypted images in three RGB channels.

Here,nxandmxrepresent neighboring pixels,Ndenotes the total number of pixels, and ¯mand ¯ncorrespond to the average values of pixelnxandmx.Figure 11 displays a random selection of 10000 adjacent pixel pairs taken from the three channels of both the original and encrypted images.The correlation coefficients between the RGB channels of the original and encrypted images are presented in Table 2 for comparative analysis.According to the analysis, the correlation coefficients of the original image are close to 1,while the encrypted image exhibits correlation coefficients approaching zero in all directions.This indicates that the proposed encryption system possesses a robust level of security.

Information entropy serves as a critical metric for assessing the randomness of encrypted image pixels.A high information entropy in encrypted images indicates excellent randomness properties within the encryption system.When computing information entropy for a color image,the image is decomposed into its three RGB channels.Each channel can be treated as an 8-bit gray-scale image,with an ideal information entropy value of 8 after encryption.Thus,a higher information entropy value indicates a more random pixel distribution and better encryption performance.Table 2 presents the measured information entropy of both the original and encrypted images in this experiment.The research findings indicate that encrypting the image significantly enhances its information entropy,approaching the theoretical maximum value of 8.These results provide strong evidence for the effectiveness of the encryption method employed,as well as the heightened level of randomness achieved within the encrypted image.

4.3.NPCR and UACI

The examination of subtle variations in the original image and their impact on the encrypted image enables the exploration of potential vulnerabilities that can be exploited to crack the encryption.To evaluate the robustness of encryption algorithms against differential attacks,metrics such as the number of pixel change rate (NPCR) and unified average change intensity (UACI) can be utilized.These metrics are valuable for assessing the effectiveness of encryption algorithms in resisting differential attacks.For two original images that have slight differences, the NPCR and UACI of the corresponding encrypted imagesPandFcan be defined as follows:

whereP(i,j)andF(i,j)represent the encrypted data obtained from different pixels in the encrypted image.The variablesmandndenote the total number of pixels in the image.In the case of 8-bit images,the threshold for NPCR and UACI is defined as follows:

Table 3 presents the NPCR and UACI results for four test images.The results indicate that the designed encryption scheme exhibits certain advantages in terms of resisting differential attacks.

Table 3.UACI and NPCR values of test images.

4.4.Robustness to noise and data loss

During the transmission or storage of images, they are vulnerable to noise or data attacks that can result in the distortion of image information.This requires encryption algorithms to be robust and resist such noise attacks and data tampering during information transmission.To conduct the counter-evidence experiment,we chose Lena as the test image and introduced various types of noise and data loss to evaluate the resilience of the image encryption algorithm.Figure 12 shows the test results of resistance to noise attacks and data loss.The encrypted image was subjected to various densities of Gaussian, salt-and-pepper, and multiplicative noise.After decryption, the encrypted image with missing data in certain regions was successfully restored to its original form.From Fig.12, we demonstrate that although certain pixel values in the decrypted image have altered,the encryption scheme successfully retains the approximate information of the original image.This indicates that the proposed encryption scheme exhibits resilience against noise attacks and data loss,thereby ensuring enhanced security.

Fig.12.Robustness analysis: (a1) encrypted image with 0.05% Gaussian noise added; (b1) encrypted image with 1%salt-and-pepper noise added;(c1)encrypted image with 1%multiplicative noise added;(d1)encrypted image with one-sixteenth data loss;(a2),(b2),(c2),and(d2)are the decrypted images corresponding to(a1),(b1),(c1),and(d1),respectively.

5.Analog circuit design

In this section, we utilized simulated operational amplifiers, analog multipliers, resistors, capacitors, and diodes to design and implement the mHNN.Our initial step involved designing a circuit module(Fig.13(a))to approximate the hyperbolic tangent function.[48]The circuit module for approximating the hyperbolic tangent function(Fig.13(a))comprises two operational amplifiers(U1,U2),two diodes(D1,D2),and four resistors(RA,RB,RC,RD).This circuit topology is simpler compared to the hyperbolic tangent function circuit modules designed in previous literature.[49]The practicality of implementing the hyperbolic tangent function is demonstrated by the input-output relationship of the approximate circuit module,which can be represented asv=tanh(vi).This is achieved by utilizing two 1N4007 diodes and setting the four resistors to specific values:RA=0.9 kΩ,RB=0.5 kΩ,RC=0.5 kΩ,andRD=0.5 kΩ.In accordance with scientific and technical writing conventions, a circuit module for the hyperbolic-type memristor was designed as described in Ref.[50],as depicted in Fig.13(b).The memristor emulator module demonstrates a defined input-output relationship,which can be expressed as

whereRk=R/k(kΩ),Ra=gR/b(kΩ),Rb=R(Ra+R)/(aRa-R)(kΩ),and the gain of the multiplierM,denoted byg,is set to 1.

Figure 13(c) illustrates the circuit diagram of the hyperbolic-type mHNN, which consists of three capacitors and one hyperbolic-type memristorW.This configuration incorporates four dynamic components associated with the state variablesx1,x2,x3, andx4, as described by the mathematical model in Eq.(4).The circuit equations are derived from the circuit schematic depicted in Fig.13:

Given fixed values ofR(10 kΩ)andC(100µF),the remaining resistor values can be computed using the element values from the synaptic weight matrix,Eq.(3),in the following manner:

Figure 14 depicts the phase trajectory obtained from the Multisim system simulation circuit, confirming the existence of coexisting bistable modes in the hyperbolic-type mHNN model.This validation is based on specific parameter values:k=0.35,a=1,b=0.1,Rk=R/k=10/0.35=28.5714 kΩ,Ra=gR/b=10/0.1=100 kΩ,andRb=R(Ra+R)/aRaR=10(100+10)/100-10=1 kΩ.

Fig.13.The circuit implementation schematic of the hyperbolic-type memristor HNN: (a) tanh(·) circuit module; (b) memristor emulator module;(c)main circuit module.

Fig.14.The experimental results illustrate phase plane plots showing the coexistence of chaotic and periodic attractors.

6.Conclusions

This paper introduces a novel circuit simulation of a three-neuron Hopfield model using hyperbolic memristors and demonstrates its effectiveness in image encryption.Nonlinear analysis techniques, including two-parameter maximum Lyapunov exponent plots, bifurcation diagrams, attractor basins,and phase trajectory diagrams, reveal the presence of asymmetric attractors and bistability in the system model.The designed color image encryption algorithm outperforms existing methods in correlation,information entropy,resistance to differential attacks, noise robustness, and data loss prevention.To support the validity of the results, an improved modular circuit design method is employed to create the analog equivalent circuit of the proposed model, which is rigorously validated using the Multisim environment.This validation process provides strong evidence for the accuracy and reliability of our numerical findings.

Therefore, future research can further explore the application of memristive neural networks in areas such as data security, communication systems, and pattern recognition.It is necessary to conduct in-depth investigations into circuit hardware implementations based on memristors,such as dedicated memristor chips or integrated circuits,to fully harness the potential of memristive neural networks in various practical applications.In conclusion, this study not only demonstrates the effectiveness of the proposed circuit simulation method in image encryption but also establishes a foundation for further exploration of memristive neural networks in various applications.By expanding the scope of applications and addressing security issues, the prospects for chaotic system applications will be further enhanced.

Acknowledgements

Project supported by the National Nature Science Foundation of China (Grant Nos.51737003 and 51977060) and the Natural Science Foundation of Hebei Province (Grant No.E2011202051).