Singular optical propagation properties of two types of one-dimensional anti-PT-symmetric periodic ring optical waveguide networks

Yanglong Fan(樊阳龙), Xiangbo Yang(杨湘波), Huada Lian(练华达), Runkai Chen(陈润楷),Pengbo Zhu(朱蓬勃), Dongmei Deng(邓冬梅), Hongzhan Liu(刘宏展), and Zhongchao Wei(韦中超)

Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices,School of Information and Optoelectronic Science and Engineering,South China Normal University,Guangzhou 510006,China

Keywords: anti-PT-symmetric,waveguide networks,bidirectional transparent

1.Introduction

In quantum mechanics, the Hermitian Hamiltonian determines the real eigenvalues.However, in 1998, Benderet al.[1,2]discovered that non-Hermitian Hamiltonians with parity-time (PT) symmetry can also exhibit real eigenvalues.In 2007, El-Ganainyet al.[3-5]introduced the concept ofPT-symmetry from mechanical systems to optical systems by constructing an optical system,in the paraxial approximation,with a refractive index that satisfies the conditionn(x)=n*(-x).PT-symmetric optical systems exhibit many peculiar optical properties,including coherent perfect absorption lasers(CPA-laser),[6,7]unidirectional invisibility,[8]birefringence,[4]new solitons,[5,9,10]nonreciprocal behavior,[4,11,12]optical switches,[13]optical bistability,[14]and so on.

In 2013,Geet al.[15]constructed an anti-PT-symmetric optical system with the refractive index of the material satisfyingn(x)=-n*(-x), following the construction method ofPT-symmetric optical systems.The system demonstrated novel properties, such as a flat total transmission band, spontaneous phase transition of the scattering matrix, and continuous laser spectra, which were distinct from those of classical systems.[15]Additionally, in 2016, Penget al.[16]experimentally constructed an anti-PT-symmetric optical system in a hot atomic vapor cell and demonstrated that it can achieve linear or nonlinear interactions between two spatially separated beams.Anti-PT-symmetric optical systems are intriguing and novel artificial optical structures that exhibit many extraordinary optical properties,[16-20]such as refractionless light propagation,[16]coherent perfect absorption lasers (CPA-laser),[17]chiral mode conversion,[18]flat broadband light transport,[19]and coherent optical switching.[20]

However, most of the research on optical anti-PTsymmetry has focused on photonic crystals.In 1998, optical waveguide networks were proposed as a new type of photonic bandgap (PBG) structures.[21]Optical waveguide networks exhibit higher structural symmetry and greater flexibility compared to photonic crystals, and they also provide more convenient methods for measuring phase and electromagnetic wave amplitudes.[21-23]Various interesting optical properties and phenomena have been demonstrated in optical waveguide networks,such as extremely wide PBGs,[23,24]comb-like transmission spectra,[25,26]and ultra-strong photonic localization.[27,28]These discoveries provide new possibilities for optical communication and sensing, and are expected to promote the development of new types of optoelectronic devices.Therefore, optical waveguide networks are also suitable for constructing optical anti-PT-symmetric structures.

In recent studies, Xuet al.[29]discovered extremely strong and weak transmission phenomena in one-dimensional three-material anti-PT-symmetric optical waveguide networks using the method of searching for weak and strong extremum spontaneous symmetry breaking points.Chenet al.[30]defined extreme mode points of anti-PT-symmetric optical waveguide networks and found that they exhibit extremely strong transmission and reflection phenomena near these points.However, it is unknown whether anti-PTsymmetric optical waveguide networks can exhibit other optical propagation properties similar to those of anti-PTsymmetric photonic crystals.Additionally, since the imaginary parts of the refractive indices of the materials in an anti-PT-symmetric optical system are the same,two systems composed entirely of gain or loss materials can be constructed,and the electromagnetic wave transmission properties of these two systems will be significantly different.What are the similarities and differences in the singular light transmission characteristics of the two systems composed of gain or loss materials? How can these characteristics be controlled? These questions have garnered significant interests.

To address the above issues,in this paper we propose two types of one-dimensional (1D) anti-PT-symmetric periodic ring optical waveguide networks(APTPROWNs).It is found that in the gain system,there is a phenomenon of electromagnetic (EM) wave ultra-strong transmission and bidirectional reflection,while in the lossy system,there is a phenomenon of equal transmittance and reflectance.In both the systems,a new type of total reflection phenomenon occurs.Moreover, when the imaginary part of the refractive index of the waveguide is less than 10-5, both the systems exhibit bidirectional transparency with transmittanceT →1 and reflectanceR ＜10-8in certain wavelength ranges.When the imaginary part of the refractive index of the waveguide is equal to 0, the systems exhibit bidirectional transparency throughout the entire wavelength range.In addition,this study found that by adjusting the number of unit cells and the length ratio of the upper and lower arm waveguides in the unit cell, these singular optical transmission properties can be effectively controlled.This paper not only deepens the understanding of the transmission properties of anti-PT-symmetric optical systems, but also provides new ideas for designing novel optical devices with singular properties,which has potential practical applications.

The structure of this article is as follows.Section 2 introduces the two types of 1DAPTPROWNs, and the network equations, generalized eigenfunction method, and scattering matrix theory used to calculate the system’s transmittance and reflectance.Section 3 describes the four singular optical propagation properties that are discovered in this study, which include ultra-strong transmission and bidirectional reflection, a new type of total reflection,size-adjustable equal transmission and reflection, and bidirectional transparency bands.Finally,Section 4 summarizes the research findings and discusses the future development of anti-PT-symmetric optical systems.

2.Model,theory and method

2.1.Model

This paper designs two types of 1DAPTPROWNs, as shown in Fig.1.Figure 1(a)illustrates 1DAPTPROWNs composed of gain material, which include three types of waveguides: gray waveguides with refractive indexn0, red waveguides with refractive indexn1, and orange waveguides with refractive indexn2.Figure 1(b)shows 1DAPTPROWNs composed of loss material, which include three types of waveguides: gray waveguides with refractive indexn0,blue waveguides with refractive indexn3,and green waveguides with refractive indexn4,

wherenais the imaginary part of the refractive index.The two ways for achieving a complex refractive index in a material are by modulating the material density[27]or by doping gain or loss quantum dots.[31]

Fig.1.Structural schematic diagrams of 1DAPTPROWNs with N unit cells: (a) a system composed of gain material, (b) a system composed of loss material.

2.2.Network equations and generalized eigenfunction method

The optical waveguide networks studied in this paper consist of three types of waveguide segments made of different materials.However,each waveguide segment is composed of a single material.Thus, we can utilize the network equation for a single material[32]to perform calculations:

The functions coth and csch represent hyperbolic cotangent and hyperbolic cosecant,respectively,zi,j=inijω/c,qdenotes the number of waveguides between adjacent nodes,dqrepresents the length of the waveguides between nodesiandj.

In a network withNunit cells, there are 2N+1 nodes,and the network equations allow for deriving 2N+1 equations describing the wave functions at each node.At the input and output ports, the transmission and reflection coefficients are treated as generalized wave functions, and two additional equations are written.Solving for the eigenvalues of the coefficient matrix that describes the transformation between the wave functions at each node allows us to obtain the transmission coefficienttandrreflection coefficient of the network.Finally,the transmission and reflection rates of the system can be calculated by taking the square ofT=|t|2andR=|r|2,respectively.

2.3.Scattering matrix theory

In conventional optical scattering structures, symmetric reflection and transmission spectra are typically observed.However,in anti-PT-symmetric optical systems,new scattering phenomena can arise due to the combination of real and imaginary parts of the refractive index, which have different symmetries.The transmission matrix interconnects the amplitudes of the electromagnetic waves on both sides of the scatterer,while the scattering matrix links the incoming and outgoing waves.Although mathematically equivalent,the scattering matrix is more relevant to anti-PT-symmetry,making it more convenient for analyzing reflection and transmission spectra in anti-PT-symmetric systems.The scattering matrix of an electromagnetic wave is defined as[33,34]

whererN,L,rN,R,andtNare the left reflection coefficient,right reflection coefficient, and transmission coefficient, respectively,of the system containingNunit cells.

In anti-PT-symmetric optical systems,the left reflection coefficient is the complex conjugate of the right reflection coefficient,[15]that is,

Obviously,it can be inferred that

LetrN,L=a+ib,thenrN,R=a-ib.Substituting it into Eq.(6)yields

The eigenvalues of the scattering matrix have an analytical form indicating that the system has two phases.When|tN|＞b,bothsN-1andsN-2are real,and|sN-1|̸=|sN-2|,resulting in amplification and attenuation of the system’s transmittance.This phase is referred to as the anti-PT-symmetric phase.[15]When|tN|＜b, bothsN-1andsN-2are complex, and|sN-1|=|sN-2|,resulting in two scattering eigenstates of the system with equal scattering intensity.This phase is known as the anti-PTsymmetric broken phase.[15]At|tN|=b, the system transits from the anti-PT-symmetric phase to the anti-PT-symmetric broken phase,or vice versa,which we refer to as the anti-PTsymmetric breaking point.It has been observed that there are significant differences in the optical transmission properties of the system between the anti-PT-symmetric and anti-PTsymmetric broken phases.

3.Results and discussion

3.1.Ultra-strong transmission and bidirectional reflection

Previous studies[32,35,36]have shown that there is a conservation relation among transmittanceT,left reflection coefficientRL,and right reflection coefficientRRinPT-symmetric systems:

According to the generalized conservation relation, it can be deduced that when the transmittanceT=0,the left and right reflection coefficients satisfyinPT-symmetric systems, while no similar conservation relation can be derived in the anti-PT-symmetric system studied in this paper.However, in the 1DAPTPROWNs composed of gain waveguides,there exists an ultra-strong transmission and double reflection phenomenon in which both the transmittance and the left and right reflection coefficients tend to infinity simultaneously.This phenomenon is caused by the resonance between electromagnetic waves and the system.When electromagnetic waves are incident at the resonance frequency, a strong resonance effect occurs after the propagation through the system.In our studied system,this resonance effect is manifested as the long confinement of reflected and transmitted electromagnetic waves and eventually results in ultra-strong transmitted and double-reflected electromagnetic waves under the extremely amplified effect of local gain.

In Figs.2(a) and 2(b), we can see that whenω ＜0.316955πc/d,|s1|̸=|s2|, the system is in the anti-PTsymmetric phase; whenω ＞0.316955πc/d,|s1|=|s2|, the system is in the anti-PT-symmetric broken phase, andω=0.316955 is a broken point for the anti-PT-symmetric of the system.

Fig.2.Ultra-strong transmission and bidirectional reflection properties of gain material 1DAPTPROWNs with four cells: (a)spectral diagram of S matrix eigenvalues, (b) spectral diagram of transmission and reflection rates, (c) spectral diagram of phase for transmitted wave, left reflected wave,and right reflected wave.

The system exhibits the phenomena of ultra-strong transmission and bidirectional reflection in the broken anti-PTsymmetric phase, where the absolute value of the scattering matrix eigenvalues is|s1|≫|s2|≈1.5.Figure 2(c)shows that the phase of the transmitted electromagnetic wave and the reflected electromagnetic wave on the right side increases byπ,while the phase of the reflected electromagnetic wave on the left side decreases byπ:

In Fig.3,we investigate the effects of the number of unit cells and the ratio of the arm lengths of the upper and lower arms in the unit cell on the resonance frequency, transmittance, and reflectance of the system.In Fig.3(a), when the aspect ratio of the upper and lower arms of the unit cell remains constant and the number of unit cells increases,the system’s resonant frequency continuously red-shifts.This is due to the propagation path of electromagnetic waves within the system increases.In Fig.3(b), when the aspect ratio of the upper and lower arms within each unit cell increases while keeping the number of unit cells constant, the system’s resonant peak frequency also experiences a red-shift.This is a result of the enlargement of the unit cell’s size,which leads to a decrease in the system’s resonant frequency.However,there is no clear correlation between the transmittance at the resonant frequency and the number of unit cells or the length ratio of the unit cell arms.This optical characteristic finds practical applications for manufacturing photonic energy storage devices with high sensitivity and efficiency and in the development of optical filters.

Fig.3.Transmission spectra near the resonance point of gain material(na =-0.005) 1DAPTPROWNs with different unit cell numbers (a)and different length ratios(b).

3.2.New type of total reflection

The total reflection generated in our designed 1DAPTPROWNs is very different from traditional total reflection.While traditional total reflection occurs at the interface between two different media,the total reflection in our network is generated by quantum superposition effects at the entrance of the optical waveguide network.Furthermore,traditional total reflection requires certain conditions such as the incident angle being equal to or greater than the critical angle,and the incident light transmitting from a medium with higher optical density to a medium with thinner optical thickness.However,our designed network’s total reflection does not require any additional conditions.These differences highlight the novelty of our total reflection phenomenon.Additionally, the average energy flux density of the new total reflection is different from the traditional total reflection,with the former being only very small but not equal to 1,unlike the latter whose value is equal to 1.A novel total reflection phenomenon is observed in the 1DAPTPROWNs,which exhibits a transmittance ofT →1 and left and right reflectance ofRR=RL≈1.Figures 4 and 5 provide a more detailed analysis of this total reflection behavior in the anti-PT-symmetric system.

Figures 4(a)and 4(b)show that the new type of total reflection occurs at a specific frequency in the broken anti-PTsymmetric phase.Atω=0.333πc/d, the eigenvalues of the scattering matrix|s1|=|s2|≈1.04, and the left and right reflection coefficientsRR=RL≈1, while the transmission coefficientT →1.As seen in Figs.4(c)and 5(c),there are two types of phase changes for transmitted and reflected waves:

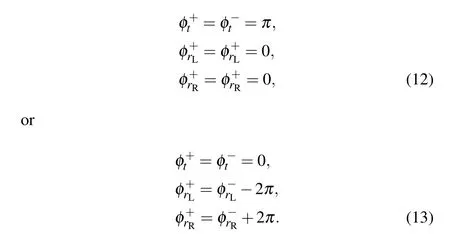
To summarize, the total reflection generated by 1DAPTPROWNs designed in this study exhibits significant differences from traditional total reflection in terms of its environment,mechanism,conditions,and average energy flow density value.These differences highlight the unique characteristics of the new total reflection generated by the anti-PT-symmetric network.

Fig.4.The total reflection characteristics of gain material (na =-0.005) 1DAPTPROWNs with four cells in the frequency range of [0.32πc/d,0.35πc/d].(a) Eigenvalue spectrum of the S matrix.(b)Spectra of transmittance and reflectance.(c)Phase spectra of transmitted wave,left reflection wave,and right reflection wave.

In Fig.6, we investigate the effects of the number of unit cells and the length ratio of the upper and lower arms of the ring resonators on the novel total reflection.In Fig.6(a),it

Fig.5.The total reflection characteristics of gain material (na =-0.005) 1DAPTPROWNs with four cells in the frequency range of [0.49πc/d,0.51πc/d].(a) Eigenvalue spectrum of the S matrix.(b)Spectra of transmittance and reflectance.(c)Phase spectra of transmitted wave,left reflection wave,and right reflection wave.

Fig.6.Transmission spectra of gain material (na =-0.005) 1DAPTPROWNs near the anti-resonance point for different unit cell numbers(a)and different length ratios(b).

is observed that the resonant frequency is independent of the number of unit cells,but the transmittance at the resonant frequency exponentially decreases with the increase of the number of unit cells.This is because the novel total reflection is an essential characteristic of 1DAPTPROWNs, which is related to the structure of the unit cell rather than the number of unit cells.Increasing the number of unit cells strengthens the anti-resonance effect of the system, leading to a continuous decrease in transmittance.In Fig.6(b), it is shown that the resonant frequency of the novel total reflection continuously red-shifts with the increase of the length ratio.Increasing the length ratio can also reduce the transmittance at the resonant frequency of the novel total reflection,but the decay rate is much slower than that of increasing the number of unit cells.This optical characteristic holds promise for practical applications in the fields of optical communication and optical switching.

3.3.Size-tunable equal transmittance and reflectance

We discuss the general properties of phase transitions in one-dimensional anti-PT-symmetric systems, which are independent of whether the system is composed of gain or loss materials.In Fig.1(b),we flip the sign of the imaginary part of the waveguide refractive index,transforming the system composed of gain materials into one composed of loss materials.The new system undergoes a time reversal compared to the original system,and the phase transition occurs at exactly the same position.As the 1DAPTPROWNs is composed of loss materials at this point,there is no gain mechanism for electromagnetic waves,making it impossible to produce ultra-strong transmission and bidirectional reflection.In this case,the resonance and loss of the system reach a balanced state,resulting in an equal transmittance rateT, left reflection rateRL, and right reflection rateRR, known as the phenomenon of equal transmission and reflection.

Fig.7.The equal-transmission-and-reflection point of loss material(na=0.005)1DAPTPROWNs with four cells: (a)eigenvalue spectrum of s matrix,(b)spectra of transmittance and reflectance,(c)phase spectra of the transmitted wave,left and right reflected waves.

In Fig.7(a), we observe that the phase transition of the new system is the same as that of the original system, with a point of anti-PT-symmetry breaking for the new system.The frequency position of the point of equal transmission and reflection occurs at the anti-PT-symmetric phase in Fig.7(a).Atω=0.3121πc/d, the transmission rateTand the left and right reflection ratesRLandRRare equal for the system.At the equal-transmission-and-reflection point, the phase of the transmitted wave and the reflected waves on the left and right sides do not undergo a sudden change and are continuous.

In Fig.8, we show the effects of different unit cell numbers and waveguide length ratios on the equal-transmissionand-reflection point.In Fig.8(b),we can see that the position of the equal-transmission-and-reflection point shifts to the red with increasing unit cell numberNand length ratiod2/d1.Its magnitude decreases with increasingNand increases with increasingd2/d1.The size-tunable equal transmittance and reflectance property can be used in the manufacturing of optical modulators.

Fig.8.The positions and magnitudes of equal-transmission-andreflection points in lossy material 1DAPTPROWNs with different unit cell numbers(a)and different length ratios(b).The blue triangle represents the frequency position and the red rectangle represents the values of transmittance and left/right reflectance.

3.4.Bidirectional transparent band

We realize that the system’s phase transition position is independent of the use of gain or loss materials.However,when the local gain or loss is zero,the system always remains in the anti-PT-symmetric phase.[10]In Fig.9, we gradually reduce the imaginary part of the material refractive index and observe that when it decreases to 0.0001, the system generates bidirectional transparent bands withT=1 andR ＜10-8in some frequency bands.These bands are represented by the gray parts of Figs.9(d)-9(f).As the imaginary part of the refractive index decreases,we also observe that the frequency range of these bidirectional transparent bands continuously expands.

In Fig.10,we plot the transmission and reflection spectra of 1DAPTPROWNs with a refractive index imaginary part ofna=0.It is found that when the refractive index imaginary part of the material that makes up the waveguide network becomes zero, a bidirectional transparent band with a transmission rate ofT=1 and a reflection rate ofR ＜10-8is formed throughout the entire band.

In addition, we investigate the robustness of the bidirectional transparency band in the systems.In Fig.11, we vary the ratio of the length of the primitive cell waveguide and find that the bidirectional transparency band still appears under different waveguide length ratios.Moreover,as the waveguide length ratio decreases,the wavelength of the bidirectional transparency band shifts towards the blue end, and the range of the bidirectional transparency band in the long-wavelength region gradually increases while that in the short-wavelength region gradually decreases.These results indicate that the system has good robustness.This discovery holds potential applications in the field of optical stealth.

Fig.10.The transmission and reflection spectra of 1DAPTPROWNs with a single cell and a material refractive index imaginary part of na=0.

Fig.11.Transmittance and reflectance spectra of 1DAPTPROWNs with a single unit cell of different waveguide length ratios, with the imaginary part of the refractive index of the material na = 10-7 for different waveguide length ratios: (a) d2/d1 = 2.08, (b) d2/d1 = 2.04,(c)d2/d1=2.02,(d)d2/d1=2.00,(e)d2/d1=1.96,(f)d2/d1=1.92.

4.Conclusion

We have investigated the transmission properties of 1DAPTPROWNs, and found some novel properties such as ultra-strong transmission and bidirectional reflection, new type of total reflection, size-tunable equal transmittance and reflectance, and bidirectional transparent bands.These findings have practical applications in creation of highly sensitive and efficient photonic energy storage devices, optical switches,and optical filters,further deepening our understanding of anti-PT-symmetric optical systems.Furthermore, the research provides new ideas and methods for solving challenges and problems in fields such as quantum information processing, optical communication, and optical sensing.Future studies could explore the transmission properties of anti-PT-symmetric optical systems with different structures and sizes,as well as their interactions with other physical systems,such as in nonlinear optics and topological physics.These studies can promote the development of optical science and provide potential solutions for developing advanced,efficient,and multifunctional optical devices.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.11674107,61475049,11775083,61774062,and 61771205).