Diffraction deep neural network-based classification for vector vortex beams

Yixiang Peng(彭怡翔), Bing Chen(陈兵), Le Wang(王乐), and Shengmei Zhao(赵生妹),2,3,†

1Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications(NJUPT),Nanjing 210003,China

2Key Laboratory of Broadband Wireless Communication and Sensor Network Technology,Ministry of Education,Nanjing 210003,China

3National Laboratory of Solid State Microstructures,Nanjing University,Nanjing 210093,China

Keywords: vector vortex beam,diffractive deep neural network,classification,atmospheric turbulence

1.Introduction

The vector vortex beam (VVB) has attracted significant attention due to its intrinsic diversity of information and has found great applications in both classical and quantum optics.[1,2]Unlike a scalar vortex beam,a VVB also has a polarization state,which varies in space.[3]It adds an information dimension to greatly increase the communication system’s capacity.Therefore, the design and demonstration of reliable techniques for the classification of VVBs are highly desirable.For example,convolutional neural networks(CNNs)and principal component analysis were used to classify the specific polarization patterns of VVBs in Ref.[4].

Unlike a CNN, which relies on the high performance of electronic components, such as CPUs and GPUs, and has increasing energy requirements for parallel computing execution,an all-optical deep learning framework was proposed by Linet al.in 2018 to create a deep learning system with almost zero energy consumption and zero latency.[5]Here, the neural network was physically formed by multiple layers of diffractive surfaces that worked in collaboration to optically perform an arbitrary function, and it was named a diffractive deep neural network(DDNN).It has provided a powerful tool for optical processing.Nowadays, all-optical signal processing of vortex beams with DDNNs has been demonstrated,including orbital angular momentum (OAM) generation, OAM identification, OAM conversion, OAM logical operation and OAM optical signal processing communication (OAM-shift keying, OAM multiplexing and demultiplexing, and OAMmode switching).[6-10]Additionally, a DDNN was applied in adaptive optics to quickly extract the characteristics of the distorted intensity caused by oceanic turbulence in time.[11-13]However, works about DDNNs for the VVB’s classification are less far discussed.

In this paper, we propose a classification scheme based on a DDNN to classify VVBs distorted by atmospheric turbulence (AT).VVBs with continuously changing polarization states on the equator of the higher-order Poincar´e sphere(HOPS) are selected as targets for classification.A DDNN is designed and trained to capture the category feature of the distorted intensity distribution.VVBs can be classified when a different polarization feature is input to the trained DDNN.Numerical simulations and an experiment are carried out to test the classification accuracy rate.Here, the polarization properties of VVBs are used as the category features, so that the classification of VVBs can be performed for continuously changing polarization states.

There are some advantages to using the proposed scheme for VVB’s classification.(i) The proposed classification scheme is demonstrated to have a higher classification accuracy than CNNs for both simulations and experiments.(ii)Compared to the classification method with a CNN, the proposed scheme is simpler with a quick training convergence,and the classification accuracy is higher,especially for strong AT.(iii) In comparison to commonly used pattern recognition algorithms,such as a support vector machine(SVM),[25]the proposed scheme exhibits a higher classification accuracy from weak AT to strong AT,without dimensionality reduction on high-dimensional data.(iv) The proposed classifier will have almost zero energy consumption and zero latency when it is physically fabricated.

2.Theory

A schematic diagram of the DDNN-based classification scheme is shown in Fig.1.A VVB passes through a phase screen that simulates AT, and its wavefront is distorted by AT.A polarizer set to the horizontal polarization direction is placed in the path of the distorted VVB, where the polarizer is a material that allows only light waves oscillating in one direction to pass through.Here,only the horizontal polarization component of the distorted VVB is passed.The extracted feature is then input to the trained DDNN, which performs the diffraction calculations on the input and obtains the classification results on the detection plane.The detection plane is divided into multiple square regions, with each region corresponding to one VVB.

Fig.1.The concept diagram of the DDNN-based classification scheme.

In general,a VVB[14,23]can be mapped geometrically by using the HOPS and expressed as

whereα ∈[0,π],β ∈[0,2π],LGℓprepresents the Laguerre-Gaussian(LG)mode,pis the number of the radial index andlis its topological charge.The unitary vectors ˆeRand ˆeLrepresent the right and left circular polarization vortices.

The thin-sheet phase screen model is used to simulate AT aberration[16]in this paper.The random phase screen matching the fluctuations of the index of refraction can be evaluated as the Fourier transform of a complex random distribution with a varianceσ2:

Here,Φn(kx,ky)is the spectrum of fluctuations in the index of refraction;it can be expressed as[15]

where FFT is the fast Fourier transform,Ris anN×Narray of complex random numbers,Φn(kx,ky) is the spectrum of fluctuations in the index of refraction,C2nis the structure constant of the index of refraction representing the strength of turbulence,L20is the outer scale of turbulence that is the largest eddy size formed by injection of turbulent energy,kl=3.3/l0,l0is equal to the inner scale of turbulence andki(i=x,y) is the wavenumber in directioni.

It is known that the right/left circular polarization can be expressed by the Jones vector representation[17,18]as

Hence,the horizontally polarized component of the VVB is

where|ψ〉His the horizontally polarized component of|ψ〉.Further,with the assumption that there is no birefringence introduced by the atmospheric turbulence,the polarized component of the VVB can be treated independently.[20-22,24]That is,the horizontally polarized component and the vertically polarized component can propagate separately through the atmospheric turbulence.Hence, the horizontal component of the distorted VVB caused by turbulence should be equal to the horizontal component of the VVB that propagates through the turbulence.Then the distorted feature(the horizontal polarization component)is extracted as

whereAis the amplitude component of the LG mode;the Fourier expansion form of eiφturb is equal to∑µBµ(θ)exp(iµφ).[19]Here,αis set toπ/2.The feature has different orders of AT interference itemµ,which leads to the distortion of the VVB.

Following the Rayleigh-Sommerfeld diffraction theorem,each pixel on the diffractive layers of a DDNN is a DDNN node and can be considered as a secondary source of a wave.[5]Hence, the Fresnel diffraction theory can be used to simulate the forward propagation of the feature beam between the diffractive layers of the DDNN.[11]Then the forward propagation of the DDNN can be described as

whereul(x,y)is the input light field of thel-th diffraction layer in the spatial domain.FFT-1represents the reverse Fourier transform.The output of the(l-1)-th diffraction layer in the frequency domainUl-1(fx,fy)=FFT(ul-1(x,y)·tl-1(x,y)),where FFT is the Fourier transform and the transmission coefficient of the nodetl(x,y)=al(x,y)exp(jφl(x,y)) is composed of amplitude and phase modulation parameters.In the paper, five diffraction layers are adopted, and they are set to the amplitude modulation, i.e., the training parameters areal(x,y).Based on the Fresnel diffraction theory, the transform functionH(fx,fy) can be expressed as exp(jkz)exp（-jλz（f2x+f2y））, wherezrepresents the separation distance between the diffractive layers andkis the wavenumber.

During the training process, the Adam gradient descent optimizer is adopted, which works with the error backpropagation algorithm.The cross-entropy is selected as the loss function and is described as

where ˆyandyrepresent the output of the DDNN and the ground truth, respectively.Specifically,yrefers to the premade category tags, while ˆyrepresents the Softmax logistic regression of the beam energy value on the regions of the detection plane, which can be expressed as ˆy=Softmax(|ud1(x,y)|2,|ud2(x,y)|2,...).The value ofidepends on the number of categories.Due to the interference from other regions on the detection plane,a summation strategy for the pixel values of the region’s light intensity is used to amplify the differences.Therefore, the energy distribution percentage(EDP)can be expressed as

whereudt(x,y)indicates the category to which the current feature belongs.

3.Results and discussion

To demonstrate the proposed DDNN-based classification scheme for VVBs,we present the experiments in this section.

The random phase screen model is used to simulate AT, and distorted VVBs with different polarization states are generated by LabVIEW 2020.The refractive index structure constantC2nfor AT is set from 1×10-15m-2/3to 1×10-12m-2/3, representing weak, medium and strong turbulence.The dataset consisted of 22000 paired data, the distorted VVB caused by AT and their ground truth, in which 20000 are used for the training and 2000 are used for the testing.Each diffractive layer has 200×200 pixels(nodes).The DDNN used the Adam optimizer to train with 50 epochs; the learning rate is 0.01.The training is based on the TensorFlow 2.7 framework.

Fig.2.The experimental setup of the VVB classification scheme based on a DDNN.HWP: half-wave plate, PBS: polarization beam splitter,SLM:spatial light modulator,CCD:charge-coupled device camera,L1-L5: amplitude-modulated diffraction layers.

Figure 2 shows the experimental setup of the proposed DDNN-based classification scheme for VVBs.The laser emits a Gaussian beam with a beam waist of 0.35 mm and a wavelength of 633 nm.The Gaussian beam passes through a polarizer to produce linearly polarized light.A half-wave plate(HWP) and a vortex retarder are used to generate a series of VVBs with continuously changing polarization states located at the equator of the HOPS.The required VVBs are generated by rotating the HWP while fixing the vortex retarder.Then,a phase screen simulating atmospheric turbulence is loaded on the spatial light modulator(SLM1).After the VVB is reflected from SLM1, its wavefront is distorted.Then, a polarization beam splitter (PBS) is used to extract the horizontally polarized part of the VVB, which is used as a category feature in our proposed scheme.The horizontally polarized part of the VVB is used as the incident beam to the trained DDNN,where L1,L2,...,L5 are the five predicted amplitude distributions of the five diffraction layers in the trained DDNN:L1 is the input layer, L5 is the output layer, and L2, L3, L4 are the hidden layers.The distributions of the five diffractive layers are obtained by simulation,and they can be solidified and fabricated by a device such as a 3D printer.Because it is the amplitude modulation for each diffraction layer in the work that cannot be realized in our lab at this moment,we record the extracted feature with a charge-coupled device (CCD) at first, then we pass it through the trained DDNN, and we can obtain information on the light field intensity of the classification from the output of the trained DDNN.It should be noted that the phase screen data employed on SLM1 are not static but rather change when it is updated,even if the strength of AT is not changed.The reason is that there is a complex random number used in the generation of the phase screen data.

Figure 3 shows the prepared VVB, where figure 3(a)shows the VVB of the polarized state with continuous variation on the equator of HOPS, and figure 3(b) displays the beam intensity distribution after feature extraction.At this time, SLM1 is not loaded with atmospheric turbulence phase screens.The results show that the intensity distribution of the features changes, corresponding toβvariations whenαis fixed.Hereα=π/2 andℓ= 1.By feature extraction,VVBs with similar intensity distributions can be distinguished for identification and classification.

Figure 4 shows the demonstration of the extracted features of different polarized components and their classification on the detection plane.The AT strengthC2nis set to 1×10-13m-2/3.It can be seen that under the medium turbulence strength,the EDP of the DDNN on the detection plane is still maintained above 95%.It is indicated that distorted VVBs can be classified by the designed DDNN.

Fig.3.(a) VVB with continuously changing polarization states located on the HOPS equator.(b)Feature distribution obtained by the VVB after feature extraction.

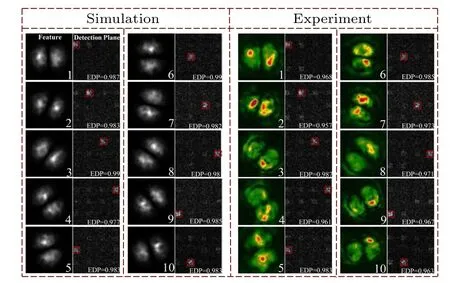
Fig.4.The demonstration of the extracted features of different polarized components and their classification.The AT strength C2n is 1×10-13 m-2/3.

We further present the EDP on the detection plane under different AT strengths in Fig.5.Here,α=π/2 andβ= 0.The results show that EDP decreases as the turbulence strength increases, because the interference in other areas of the detection plane is increased when the turbulence strength increases.Compared with the simulation results,the EDPs are reduced for the experimental results.For weak AT,the EDP for the simulation is 0.99, while it is reduced to 0.987 for the experiment whenC2n=1×10-14m-2/3.For medium AT, the EDP for the simulation is reduced, say, to 0.987 and the EDP for the experiment is reduced to 0.968 whenC2n=1×10-13m-2/3.For strong AT,the EDP for the simulation is reduced greatly to 0.863,while it is 0.831 for the experiment whenC2n=1×10-12m-2/3.

Fig.5.The demonstration of the extracted features and their classification under different AT strengths.

Figure 6(a) presents a more intuitive and comprehensive representation of EDP for each category under different AT strengths, where the EDPs of different classes under different AT strengths are displayed.It can be seen that the EDPs remain above 95%from weak to medium strength turbulence, but for strong turbulence they range between 80% and 85%.Figure 6(b) shows the classification accuracy of different classes under different AT strengths.The results show that the accuracy can remain above 95%for different strengths of turbulence,from weak to strong.

Figure 7 shows the comparison with the results using a CNN,[4]where figure 7(a) shows the classification accuracy of disturbed VVBs based on a DDNN and a CNN under different AT strengths, and figure 7(b) shows the training loss of the VVB classification scheme based on a DDNN and a CNN.Here, the CNN-based VVB classification scheme used an RGB color encoding strategy in the values of Stokes parameters to visualize the polarization patterns of VVBs.In comparison, our approach simplifies the complexity of feature extraction, where only a single polarization direction is used.Importantly, DDNN processes in optical fields, so that the proposed classification scheme can be used in the optical path without any energy consumption or latency.The results in Fig.7 show that both approaches exhibit good average accuracies in the weak and medium strength turbulence.For strong turbulence,sayC2n=1×10-12m-2/3,the average accuracy is 0.964 for the proposed scheme, while it is 0.956 by using a CNN; the proposed scheme can achieve better average accuracy.At the same time,figure 7(b)shows that the training loss of our DDNN approach has a faster convergence trend than that based on a CNN.The loss function approaches zero at 14 epochs for the proposed scheme, while it is still at 4.035 for the method using a CNN.

Fig.7.(a) The classification accuracy of disturbed VVBs based on a DDNN and a CNN.(b) The training loss of the VVB classification scheme based on a DDNN and a CNN within 50 epochs.

Table 1 further compares the accuracy of the proposed scheme with the pattern recognition algorithm under the same conditions.Here, a support vector machine,[25]which has been widely applied in image recognition and feature extraction,[26-28]is adopted.The results show that the accuracy obtained by the proposed scheme is much higher than that using the SVM.The classification accuracy is 0.96,while it is only 87%when=1×10-12m-2/3.

Table 1.The classification accuracy by using the proposed scheme and SVM.

4.Conclusion

We have proposed a vector vortex beam classification scheme based on a DDNN in this paper, where the VVB has a continuously changing polarization state.A DDNN is designed and trained, and the horizontal polarization direction of the input distorted beam is adopted as the classification feature, where the distortion is caused by AT simulated using the random phase screen model.The numerical simulation and experimental results show that the proposed scheme can accurately classify VVBs in various turbulence conditions,even in strong turbulence.The EDPs remain above 95%from weak to medium strength turbulence,and range between 80%and 85% for strong turbulence.It is indicated that the proposed DDNN-based classification scheme is highly resilient to environmental disturbances.In comparison with the CNNbased and SVM-based classification approaches,the proposed scheme has advantages in feature extraction,data preprocessing,performance and physical realization.The horizontal polarization direction of the input distorted beam is used as the classification feature in the proposed method.Hence,it is simple but has some limits on the input distorted beam,for example, only the equator of HOPS VVBs can be distinguished.With more information extracted from the designed DDNN,the V-OAM detection method,V-OAM correction and demultiplexing method can be studied based on DDNNs.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.62375140 and 62001249)and the Open Research Fund of National Laboratory of Solid State Microstructures(Grant No.M36055).