Electronic effects on radiation damage in α-iron:A molecular dynamics study

Lin Jiang(江林), Min Li(李敏), Bao-Qin Fu(付宝勤), Jie-Chao Cui(崔节超), and Qing Hou(侯氢)

Key Laboratory for Radiation Physics and Technology,Institute of Nuclear Science and Technology,Sichuan University,Chengdu 610064,China

Keywords: radiation damage,electronic effects,molecular dynamics simulation,α-iron

1.Introduction

Ferritic steel is a common structural material used in current fission reactors and a candidate structural material for next-generation fission reactors.Additionally, reducedactivation ferritic/martensitic steel is widely regarded as a promising structural material for the first wall and cladding material of future fusion reactor.In reactor’s high neutron irradiation environment,these structural materials undergo significant changes in their microstructure and mechanical properties,severely degrading their performances and affecting reactor safety.[1]Considering that the matrix material of these steels is mainlyα-iron (α-Fe), it is of great significance to study the irradiation damage behavior ofα-Fe and clarify its radiation damage mechanism.

Material damage under neutron irradiation results from the diffusion, aggregation, and cluster growth of point defects.These point defects can be the neutron transmutation products or produced by the primary knock-on atoms(PKAs).PKAs originate from the energy transfer caused by neutrons when they penetrate a material,leading to a collision cascade and creating Frenkel pairs(FPs)(vacancies and self-interstitial atoms(SIAs)).The PKA-induced collision cascade can be divided into ballistic, thermal spike, quenching, and annealing phases.[2]The spatial scale and temporal scale of the entire process are on the order of picoseconds and nanometers, respectively, making it hard to observe directly in experiment.This is why simulation studies have become indispensable for the relevant researches.Among them, molecular dynamics(MD) is particularly suitable for studying the cascade evolution because it can track the motion of each atom in the system and match the spatial and temporal scales of the collision cascades.It also considers the multi-body effect and can accurately describe the formation of stable defects and defect clusters in detail on an atomic scale.Thus,MD is widely used for simulating the defect evolution in collision cascades.[3-10]

However, earlier MD simulations of cascade damage often neglect the influence of electronic effects.In fact, in the collision cascade process, in addition to the interaction between the energetic atoms and the surrounding atoms,there is an energy exchange between the atoms and the electrons.Two theories are commonly used to describe the atom-electron interaction: electronic stopping(ES)and electron-phonon coupling(EPC).The ES is derived from the atomic collision theory,which proposes that high-energy atoms experience inelastic collisions with electrons while moving ballistically in the target medium.[11]The EPC is based on the thermal conductivity theory,which assumes that the atoms oscillate near their equilibrium positions and exchange energy with the electron gas.[12]

The two-temperature MD (2T-MD) model can incorporate the aforementioned electronic effects into MD simulations.[5,13,14]For example, Duffy and Rutherford[5]simulated the cascade damage inα-Fe by using the 2T-MD model and setting the cutoff energy (Ecutoff).Both ES and EPC were considered for atoms with kinetic energy higher thanEcutoff,while only EPC was employed for atoms with kinetic energy lower thanEcutoff.Their results revealed that the EPC reduces the defects in the thermal spike phase and residual defects at the end of the simulation time while shortening the relaxation time.[6]However,applying both ES and EPC to high-energy atoms simultaneously by Duffy and Rutherford[5]is not appropriate because although ES and EPC have different theoretical foundations, they both describe the energy exchange between atoms and electrons and therefore should not be applied simultaneously to high-energy atoms.According to this,Cuiet al.[2]investigated cascade damage in tungsten(W)by using a model that introduces different electronic effects into atoms with different kinetic energy.Zhouet al.[15]used this model to simulate collision cascades in zirconium (Zr)and found that EPC reduces the defects in the thermal spike phase but increases residual defects while promoting the occurrence of subcascades and inhibiting the formation of large defect clusters.Unlike W,EPC has no significant effect on the spatial distribution of defects in Zr.[2,15]It was observed that the influence of electronic effects varies among different materials and their influence on cascade damage inα-Fe still need further detailed investigation.This work presents MD computational models with different electronic effects for simulating the cascade damage inα-Fe and systematically assessing the influence of ES and EPC on defect generation and recombination, the size distribution of residual defect clusters and subcascade formation.This work would help in understanding the formation mechanism of radiation damage and guiding the development of radiation-resistant materials.

2.Simulation method

2.1.MD computational models

Figure 1 illustrates the process of collision cascade caused by a PKA,creating two types of energetic atoms: high-energy recoil atoms, which can continue to move ballistically in the material and even directly collide with the lattice atoms, resulting in atomic displacement, and epithermal atoms, which have higher kinetic energy than lattice atoms but are not sufficient to displace atoms directly.Instead,they exchange energy with lattice atoms through vibrations.In the ballistic phase of the cascade,the PKA and high-energy recoil atoms dominate,resulting in directly knocking lattice atoms out of their positions and producing supersonic shock waves.In the thermal spike phase, the epithermal atoms in the damaged area exchange energy with the surrounding atoms,leading to atomic displacement and further expanding the damaged region.The supersonic shock wave reduces to the sonic shock wave in the propagation process.[16-18]Considering the definition of ES and EPC and the dynamic behavior of energetic atoms generated in the cascade process, this study establishes an MD computational model including electronic effects,by using ES to describe the energy dissipation when the PKA and highenergy recoil atoms interact with electrons and applying EPC to describe the energy exchange among epithermal atoms,lattice atoms(thermal atoms),and electrons.

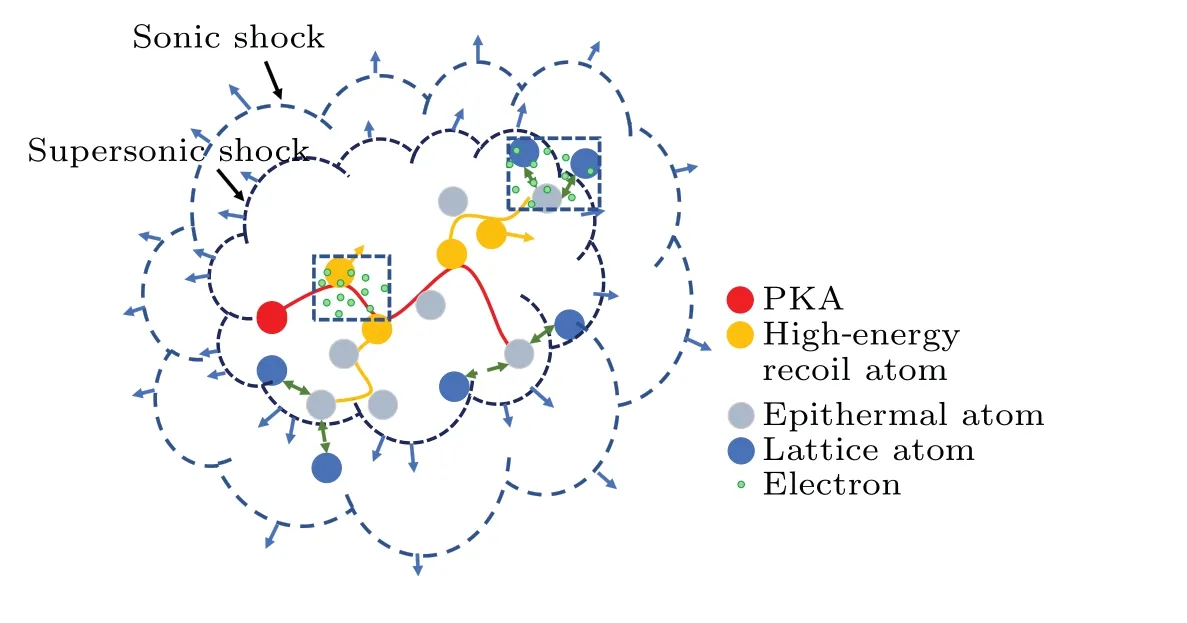
Fig.1.Schematic diagram of collision cascade.

Reference [19] described in detail the specific method,while the main idea is presented here.In a conventional MD simulation approach without electronic effect (without-ESEPC),the force acting on atomiis given by

whereUTrepresents the total potential energy of the system andxirefers to the position of atomi.When taking electronic effect into account,beside the influence of surrounding atoms, atomiwill experience the forceFeiexerted by electrons.Equation(1)can then be rewritten as follows:

For the PKA and high-energy recoil atoms, the forceFeion atomiwith velocityvidue to ES can be expressed as follows:

whereρdenotes the density of the target material,mrepresents the atomic mass, andSe(vi) refers to the electronic stopping power and can be calculated by using the SRIM program.[20]

By using EPC,the energy exchange between phonons and electrons can be expressed as follows:[19]

whereTi(t) is the atomic temperature,Tethe electron temperature, which is set to be a given temperature in this study,τEPCthe characteristic coupling time of the energy exchange between phonons and electrons,tthe time,methe electron mass,κthe thermal conductivity,εFthe Fermi velocity,ΘDthe Debby temperature,Lthe Lorentz number,nthe free electron density,ethe electron charge,kBthe Boltzmann constant,and Z the valence number.Thus,when using EPC to describe the force of electrons on epithermal and thermal atoms, the following force can be used:

The thresholdEcutoffis used to distinguish whether atomiwith kinetic energyEk,iis a high-energy recoil atom or an epithermal atom,and the value ofEcutoffis selected to be 10 eV.[21,22]If only the effect of ES on high-energy recoil atoms(with-ES)is considered,equation(2)is expressed as follows:

2.2.MD simulations

All MD simulations are performed by using the GPUaccelerated MD package MDPSCU.[23]The choice of atomic potential has an important effect on the simulation results.Thus,two embedded atom potentials,M07 potential[24,25]and M03 potential,[26]are employed for describing the interaction between Fe atoms,to explore the influence of different potentials.The M03 potential accurately reproduces the properties of small SIA clusters and dislocations, making it suitable for simulating cascade damage in Fe.[27-30]Moreover, the M07 potential further optimizes the M03 potential by accurately predicting the relative stability of C15-type clusters and has been widely used in various cases.[31-34]Table 1 presents the Fe properties calculated by using the two potentials and compared with experimental orab initioresults.

In this study,three simulation boxes of different sizes(Table 2) are constructed to simulate cascade damage caused by PKA with different energy inα-Fe, and periodic boundary conditions are adopted in all three directions.After sufficient relaxation at 300 K, thermal equilibrium is reached.Subsequently, a selected Fe atom near the center of the box is denoted as the PKA, and kinetic energy is assigned to PKA to initiate the simulation of cascade damage.The PKA directions are set to be〈100〉,〈110〉,and〈111〉,while the values of PKA kinetic energy(EPKA)are set to be 1 keV,5 keV,10 keV,and 30 keV,respectively.A variable time step is used in the simulation to ensure that all atomic displacements within a time step do not exceed the given threshold.Because the collision cascade takes place faster than the relaxation time of the material,the system is initially far from thermal equilibrium.To dissipate the excess energy from the system,the atoms in the outermost 1.5a0thickness of the box are coupled with a Berendsen thermostat.[40]In this study,the Wigner-Seitz method[41]is employed for analyzing the SIA and vacancy produced in the cascade damage process, and the residual defects of the same type which are within the third nearest neighbor distance are considered as the same cluster.For large clusters, dislocation analysis is performed by using the dislocation extraction algorithm[42,43]in the OVITO[44]program.To ensure the statistics of the simulation results,20 independent simulations are carried out under the same conditions.

Table 1.Values of lattice parameter (a0), cohesive energy (Ecoh), melting point (Tm), single vacancy formation energy (Efor1 vac), single SIA formation energy(Efor〈110〉),and displacement threshold energy(Ed)calculated with M07 potential and M03 potential and compared with experimental or ab initio results.

Table 2.Three simulation boxes for collision cascade simulation.

3.Simulation results

Herein, three MD simulation models (without-ESEPC,with-ES,and with-ESEPC)are employed to simulate the collision cascade inα-Fe and explore the role of electronic effects in cascade damage.Previous researches pointed out that the EPC characteristic coupling timeτEPCaffects the simulation results.[2,15,45,46]Thus, parameter sensitivity analysis ofτEPCis also performed.Unless otherwise stated,τEPCwas set to be 1 ps.In this section, the cascade damage caused by 30 keV PKA in the〈100〉direction is specifically introduced.The influence of cascade energy and PKA direction will be analyzed in detail later.

3.1.Role of electronic effects in cascade damage

Figure 2 shows the evolution of cascade damage obtained by using the M03 and M07 potentials.As shown in the figure, for both potentials, the number of thermal spike defectsNpeakis the highest when neglecting electronic effects and the lowest when considering both ES and EPC, indicating that electronic effects can inhibit defect generation in the thermal spike phase(Fig.2(a)).However,figure 2(b)reveals that comparing with neglecting electronic effects,the number of residual defectsNsurvivalconsistently decreases when incorporating only ES and increases when considering both electronic effects, although different interatomic potentials are employed.This phenomenon indicates that the application of ES reduces the generation of residual defects, whereas EPC has the opposite effect.For the same computational model, the application of the M03 potential consistently produces moreNpeakandNsurvivalthan the application of the M07 potential,which is attributed to the lower defect formation energy, displacement threshold energy,and melting point of the M03 potential,making it more likely to generate defects.Specifically,in Fig.2(b),neglecting electronic effects,the use of M03 potential obtains a 50%higherNsurvivalthan the use of M07 potential.However,considering ES and EPC, the difference decreases to 30%.This reveals that the introduction of electronic effects reduces the simulation discrepancy between different potentials.

In order to clarify the effects of ES and EPC on cascade damage,the same simulations are performed at first,but electronic effects are activated at different times (ta).Here, 0 ps is the onset of the cascade,tbtis the transition time from the ballistic phase to the thermal spike phase,andtpeakis the time when most defects are produced without applying electronic effects.Figure 3 illustrates the simulation results.Figures 3(a)and 3(b) demonstrate that the ES only affects the ballistic phase, when high-energy recoil atoms lose energy due to the inelastic collision with electrons and thus reduce the energy available for displacing atoms,resulting in a decrease inNpeak.Defect recombination primarily takes place during the quench phase,while the ES exclusively affects the ballistic phase.As a result,the ES does not affect the defect recombination,ultimately leading to a decrease inNsurvival.In contrast to ES,the EPC has no significant effect on the ballistic phase but can result in rapid energy dissipation in the defect region during the thermal spike phase, causing a significant reduction inNpeak.Figure 3(c)indicates that the incorporation of EPC reduces defect recombination during the annealing phase, ultimately resulting in the increase ofNsurvival.This can be attributed to the ability of EPC to transfer energy from the atomic subsystem to the electronic subsystem, thereby slowing down the speed of the atoms and lowering the temperature of the atomic subsystem.

Fig.2.Cascade damage evolution under different MD models:(a)number of FPs NFP versus time,and(b)number of residual defects Nsurvival.

Fig.3.Number of FPs NFP versus time when activating the electronic effects at different values of ta: (a)0 ps,(b)tbt,(c)tpeak.The initial states of all simulation systems are identical.The pink square indicates activation time ta.tbt means the transition point from the ballistic phase to the thermal spike phase,while tpeak refers to the time when the most defects are produced without electronic effects applied.

3.2.Influence of electronic effects on defect clustering

Fig.4.Size distribution of defect clusters: (a)SIA,(b)vacancy.

The size distribution of residual defect clusters after the collision cascade is exhibited in Fig.4, which indicates that the ES reduces the occurrence of large SIA clusters while EPC promotes the formation of single defects and small defect clusters but considerably inhibits large cluster formation(Figs.4(a)and 4(b)).This is because EPC results in rapid loss of atomic velocity in the defect recombination stage,thus precluding the defects from forming large clusters.larger maximum defect cluster than using the M07 potential,but when considering the ES and EPC, similar results can be obtained by using the two potentials,which demonstrates once again that the electronic effects can reduce the simulation discrepancies of different potentials.However, when using the M03 potential, introducing ES results in a 58-SIA cluster,which is significantly larger than the maximum cluster (containing 38 SIAs)when neglecting the electronic effects.This special case will be further analyzed later.The results of the dislocation analysis of these large clusters reveal that with the M07 potential used, no dislocation loop is formed, but with the M03 potential adopted, a 58 1/2〈111〉 SIA-type dislocation loop is formed.

Table 3.Largest defect cluster under different MD models.

Table 3 lists the maximum cluster sizes,which are consistent with the results in Fig.4.Moreover,when neglecting electronic effects, using the M03 potential obtains a significantly

Fig.5.Evolutions of cascade damage with τEPC: (a)number of FPs NFP versus time,(b)number of residual defects Nsurvival versus τEPC,size distribution of(c)SIA clusters and(d)vacancy clusters.

3.3.Effect of characteristic coupling time(τEPC)

It is challenging to determineτEPCexperimentally, however, it is estimated at several picoseconds.Thus, it is necessary to analyze the sensitivity of parameterτEPC.Additionally,this study aims to further clarify the effect of EPC on cascade damage in Fe.The With-ESEPC computational model is employed,andτEPCvalues are 1 ps,5 ps,and 10 ps,respectively.

Figure 5 illustrates the simulation results.As observed in Figs.5(a) and 5(b), a smallerτEPCvalue, which represents stronger energy exchange between phonons and electrons,leads to smallerNpeak,shorter relaxation time,and largerNsurvival, which are consistent with previous observations in Fe,[45]W,[2]and Zr.[15]This is because the strong EPC results in rapid loss of atomic velocity, thereby shortening the relaxation time and reducing defect recombination.The size distributions of the defect clusters obtained by using the two potentials(Figs.5(c)and 5(d))again reveal that EPC increases the number of single defects and small defect clusters but inhibits the formation of large defect clusters.This phenomenon becomes more pronounced with the application of stronger EPC.Moreover, the maximum defect cluster sizes in Table 4 also reflect this trend.

Table 4.Largest defect clusters with different τEPC applied.

4.Discussion

4.1.PKA energy

Figure 6 exhibits the number of residual defectsNsurvivalobtained with different values ofEPKAin the〈100〉 direction by using the M07 potential.As observed in the figure, the relationship betweenEPKAandNsurvivalcan be described by a power law function in all the three computational models:[4,47]

whereAandBare the fitting parameters.Figure 6 demonstrates that for all PKA energy, the introducing of ES can reduceNsurvivalcompared with the neglecting of electronic effects.However, the considering of both ES and EPC increasesNsurvival.B-values of 1.09,0.94,and 1.04 are measured from data fitting with the without-ESEPC,with-ES,and with-ESEPC models, respectively, pointing out that the difference inNsurvivalobtained from different computational models increases withEPKA.Similar trends are observed in the simulations using the M03 potential.Thus,electronic effects should not be neglected in the MD simulation of cascade damage,particularly high-energy cascade damage.

Fig.6.Numbers of surviving FPs Nsurvival versus PKA energy EPKA under different MD models with M07 potential applied,with dotted lines denoting fitting curves of data points.

4.2.PKA direction

Fig.7.Cascade damage evolutions induced by 30-keV PKA with different directions with the M07 potential applied: number of FPs NFP versus time in(a)〈100〉,(b)〈110〉,(c)〈111〉directions,(d)number of residual defects Nsurvival versus PKA direction.

In the above simulations of cascade damage inα-Fe,only a single〈100〉 direction is considered, which is based on an earlier study,[48]indicating that the PKA direction has no significant effect on cascade damage in high-energy cascades.[49]However,it is necessary to investigate whether this holds true when considering the electronic effects.Figure 7 illustrates the consistent effects of ES and EPC in the〈100〉,〈110〉,and〈111〉 direction using the M07 potential.Figures 7(a)-7(c)show a similar defect evolution in different directions under the same computational model.Additionally,figure 7(d)illustrates a consistent phenomenon of residual defects.It is evident that the PKA orientation has a limited effect on cascade damage.This observation is further validated by employing the M03 potential.

4.3.Subcascade formation

The above results have shown that the electronic effects can affect the formation of residual defect clusters.The defect cluster formation is closely related to the defect evolution in damaged region.In general,large defect clusters often emerge in cascades having compact damage distribution.[50]To analyze the morphology of the damaged region in the thermal spike phase, the two-point density correlation function[51]is used(Fig.8).The results reveal three types of morphologies.The first type is the unfragmented cascade,in which the entire damaged region is compact, forming a single large thermal spike region.In this case, the large SIA and vacancy defect clusters are more likely to form after defect recombination.The second type is the connected subcascade, which consists of multiple interconnected damaged regions that are separated in the subsequent quenching phase.The third type is the unconnected subcascade, which is characterized by several independent damaged regions where large-sized defect cluster formation is difficult after defect recombination.Connected and unconnected subcascades are commonly known as subcascades.The PKA energy of 30 keV used here is close to the threshold energy of subcascade formation.

Fig.8.Three cascades: (a) unfragmented cascade, (b) connected subcascade,(c)unconnected subcascade.Red and blue spheres represent SIAs and vacancies,respectively.

Thus,based on the features of the two-point density correlation function for cascade damage in Fe(Fig.9(a)), 20 independent simulations are performed when 30-keV PKAs are introduced in the〈100〉 direction (Fig.9(b)).It is revealed that with the two potentials,the number of unfragmented cascades decreases with the successive introduction of both ES and EPC, while the number of unconnected subcascades increases,suggesting that both ES and EPC can promote subcascade formation,thus inhibiting large cluster formation,which is consistent with Fig.4.Moreover, subcascade formation is more strongly influenced by electronic effects when using the M03 potential rather than the M07 potential.

Fig.9.(a) Two-point density correlation function C(r) of three cascades,with r denoting the distance between displaced atoms and Rmax the maximum size of the damage region;(b)ratios of the three cascades for three different MD models.

A subcascade is produced when one or more high-energy recoil atoms produce additional damaged regions through long-range migration.It has been suggested that electronic effects, particularly ES,will only continuously reduce the kinetic energy of these high-energy recoil atoms and eventually reduce the size of the damaged region formed by the cascade without significantly changing the geometry of the damaged region.The influence of electronic effects on the cascade damage configuration is investigated by comparing the simulation results with electronic effects with those without electronic effects in identical initial conditions(i.e.,identical positions and velocities of all atoms,including the PKA).Figure 10 reveals that at the very early stage of the cascade(around 0.02 ps),almost no difference among the three models is observed, with all exhibiting long-range migration of high-energy displaced atoms.At about 0.03 ps, the difference starts to emerge.For the without-ESEPC model,the displaced atom has higher energy and smaller forward scattering angle when colliding with lattice atoms.For the with-ES model, the displaced atom has a decrease in energy and a larger forward scattering angle upon colliding with lattice atoms.Consequently, distant damaged regions appear.In the thermal spike phase,two thermal spike regions are observed for the without-ESEPC model,while three for the with-ES model and with-ESEPC model.Our multiple independent simulations,including using different potentials,show a similar phenomenon that the ES scatters lattice atoms at a large angle,thus increasing the probability of subcascade formation.The comparison between the with-ES model and the with-ESEPC model shows that the introduction of EPC can only reduce the size of the damaged region without significantly changing its configuration,which is attributed to the rapid energy dissipation in the damaged region by EPC in the thermal spike phase.

Fig.10.Cascade evolutions in simulation systems with the same initial state: (a) without-ESEPC, (b) with-ES, and (c) with-ESEPC.Black arrows denote the motion direction of the high-energy recoil atom,and red and blue spheres refer to SIAs and vacancies,respectively.

Fig.11.Formation of a large SIA cluster induced by connected-type subcascade,with green box locating the position of 58-SIA cluster,and red and blue spheres denoting SIAs and vacancies,respectively.

Subcascades are classified as connected type and unconnected type because connected subcascades may promote the formation of large SIA cluster.[52]This is demonstrated by the presence of the 58-SIA cluster in Fig.11 and listed in Table 3,with the ES-introduced M03 potential used.Interconnected damage regions,namely,connected subcascades,occur in the ballistic phase (0.16 ps) and thermal spike phase (0.51 ps).At the end of the simulation time, a 58-SIA cluster is produced near the center of one of the damaged regions,the formation of which can be reasonably explained by the shockwave model.[53]The model proposes the formation of large cluster by the shockwave front pushing atoms into low-density regions,i.e.,the center of a particular damaged region.However, the presence of large SIA cluster in connected subcascades requires a relatively high shockwave intensity.In this work, the PKA energy is set to 30 keV, which is close to the threshold for subcascade formation.Thus,only the individual case (Fig.11) is observed.At higher PKA energy, the electronic effect becomes more significant and the probability of this phenomenon is higher.

5.Conclusions

In this work, the influences of two electronic effects, ES and EPC, on cascade damage in Fe are explored by different MD computational models.The simulation results exhibit that the ES and EPC reduce the energy of the displaced atoms and thus reduceNpeakin the thermal spike phase.Specifically,the ES causes atoms to lose kinetic energy in the ballistic phase through inelastic collision with the electrons,causing the number of defects to decrease in the thermal spike phase without affecting defect recombination.This, in turn, leads to a decrease inNsurvival.Moreover, the EPC lowers the atomic energy in the thermal spike phase and reducesNpeakas well,but it also reduces defect recombination in the quenching phase,causing an increase inNsurvival.The magnitude of this effect is more pronounced for smaller characteristic time of EPC,which promotes the phonon-electron energy exchange.The electronic effects become more prominent at higher PKA energy and facilitate subcascade formation,which can influence the residual defect cluster formation.Notably, the EPC hinders the formation of defect cluster, significantly increasing the number of single and small defect clusters.However, the ES scatters the lattice atoms at large angles,making the damaged region more discrete and thus increasing the probability of subcascade formation, but the EPC only reduces the damaged region in the thermal spike phase.Moreover, compared with neglecting the electronic effects,taking both ES and EPC into account makes the number of defects and the size distribution of defect clusters obtained at different potentials closer.The findings highlight the importance of electronic effects in understanding and predicting the material’s behavior under irradiation.

Acknowledgements

Project supported by the National MCF Energy Research and Development Program of China (Grant Nos.2022YFE03200200 and 2018YFE0308101), the National Natural Science Foundation of China (Grant No.12105194), and the Natural Science Foundation of Sichuan Province, China (Grant Nos.2022NSFSC1265 and 2022NSFSC1251).