Bearing capacity of circular footings on multi-layered sand-waste tire shreds reinforced with geogrids
2024-03-25MahmoudGhazaviEhsanKhosroshahi
Mahmoud Ghazavi,Ehsan Khosroshahi
Faculty of Civil Engineering, K.N.Toosi University of Technology, Tehran, Iran
Keywords: Geogrid Sand Waste tire shred Bearing capacity Waste tire shred optimization Tire shred aspect ratio
ABSTRACT
1.Introduction
Hundreds of millions of waste tires are discarded and stored each year,which is harmful to the environment.In the United States,more than 390 million tires are discarded annually(Zahran and El Naggar,2020).In Iran,13 million tons of tires become out of use and are sent to landfills annually(Hatami and Amiri,2022).In Canada,about 33 million tires are used each year(Wolfersdorff and Plaumann,2022).Million tons of tires become waste and cause serious problems to the environment due to their shape and size.In addition,they are flammable and can produce toxic fumes causing diseases if being ignited (Fiksel et al.,2011).Furthermore,the accumulation of waste tires in landfills might pollute aquifers.Therefore,some viable solutions have been proposed to reuse the waste tires (Lo Presti,2013).The waste tires can be used as a fuel called tire-derived fuel (TDF) for plants and as tire-derived aggregates(TDAs)for civil projects(Zahran and El Naggar,2020).TDA or tire shreds mixed with soil are used for many applications due to their low specific weight,compressibility,and high tensile strength(Humphrey,1999;Ghazavi,2004;Moghadam et al.,2018).Tires can be used for reinforcement in road construction (Bosscher et al.,1997;Heimdahl and Drescher,1999),as an additive to improve asphalt properties(Cao,2007)and to increase the bearing capacity of foundations(Hataf and Rahimi,2006;Yoon et al.,2004),;for soil erosion prevention,slope stability improvement (Poh and Broms,1995;O’Shaughnessy and Garga,2000),and backfill materials behind retaining structures (Lee et al.,1999;Reddy and Krishna,2015;Contreras-Marín et al.,2021).
For the feasibility of using shred-soil mixture in the above applications,it is necessary to evaluate the shear strength parameters and compressive properties of the mixtures.To this end,Foose et al.(1996)conducted direct shear tests on soil-tire shreds mixtures and found that adding tire shreds to the soil can increase the shear strength and the internal angle of friction from 34°to 67°.Yoon et al.(2004) carried out a series of plate load tests.They used the treads and sidewalls of the waste tires to reinforce the soil and found that when the soil was looser,the reinforcement effect on reducing settlement was more significant.Meles et al.(2014)conducted several large-scale one-dimensional (1D) compression tests to evaluate the compressive properties of TDA.Their results indicated that as the specific weight of TDA and tire shreds increased,their compressibility was reduced.Ghazavi and Amel Sakhi (2005a) performed California bearing ratio (CBR) tests on sand-tire shred(STS)mixtures at two compaction degrees and with various shred contents and aspect ratios.They reported that there would be a unique length for a specific width of the shreds,for which the CBR becomes maximum.Ghazavi and Amel Sakhi(2005b) conducted large direct shear tests on STS mixtures to determine the optimal dimensions and content of the tire shreds to achieve the maximum shear strength parameters.They concluded that the normal stress,sand matrix unit weight,shred content,shred width,and shred aspect ratio (length to width) are the primary parameters affecting the shear strength of STS mixtures.Prasad and Raju (2009) performed triaxial and CBR tests on sandrubber grain mixture samples with different weight percentages.Their results showed that the optimal rubber grain content is 5%-6%by weight.Edinçliler and Cagatay(2013)conducted CBR tests to assess the effect of rubber grains on soil behavior.They found that the rubber grains reduce the pavement layer thickness under traffic loads.Yoon et al.(2008) adopted waste tires called “tire cells” to reinforce sand.They reported that the bearing capacity is reduced for sands with increasing the unit weight.Hataf and Rahimi(2006)carried out laboratory tests on a circular footing with a 15 cm diameter located at an STS mixture with two different shred widths and found that the optimal tire shred content is 40% by volume.However,they did not use the unit weight of sand matrix and thus their results are questionable.Hataf and Rahimi (2006) and Yoon et al.(2004) used a single size of strip footing and ignored the matrix unit weight for tire-reinforced mixtures,which can result in unreliable outcomes.Furthermore,they did not use scale effects,therefore their results may be unrealistic.This shortcoming will be considered in the current study.
Waste tire shreds have been used in practical projects around the world.For example,as indicated by Dickson et al.(2001),Humphrey (1999),Humphrey et al.(2000),and Shalaby and Khan(2005),tire shred-sand mixtures are used in road construction as a layered bed.In practice,the road base is filled with 3 m of STS mixtures and overlying sand with 1 m thickness as a cap layer(Dickson et al.,2001).In the work of Dawyer(2008),the tire shreds were used in practical projects under the roadbed and road construction.These projects were administrated and supervised by New York State Department of Transportation (NYSDOT),USA.For example,more than one million of tires were used in several projects from 2005 to 2008(Dawyer,2008).Also,the estimated cost of filling each cubic meter with tire shreds and a mixture of STSs was 80-95 USD (Dawyer,2008).
The effect of replacing soil with STS mixture in reducing seismic-induced movements has been discussed in the literature(Anastasiadis et al.,2012;Pitilakis et al.,2015).Recently,Ghazavi and Kavandi (2022) determined shear modulus and damping characteristics of uniform and layered sand-rubber grain mixtures using cyclic triaxial test apparatus and reported reasonable stiffness and damping specifications for sand-rubber mixtures.
The high compressibility of tires is neglected in numerical studies,leading to an overestimated soil settlement.Therefore,the bearing capacity of the system can be improved by mixing the material with geosynthetics without any changes in the damping characteristics(e.g.Manohar and Anbazhagan,2021).Many studies have evaluated the effect of TDAs and tire shreds in the form of grains,fibers,strips,and shreds in soil-tire material mixtures on the soil shear strength and bearing capacity of foundations.However,fewer studies have been reported on simultaneous application of these mixtures and geosynthetics such as geogrid.Manohar and Anbazhagan (2021) conducted a series of unconsolidated undrained triaxial shear tests on sand-rubber mixtures reinforced with geosynthetics and found that the reinforced mixtures have a significantly improved shear strength.
In the current study,the effect of single and multi-layered STS mixtures on the bearing capacity of a circular footing has been investigated experimentally.These tests examine the effect of various parameters including shred aspect ratio,tire shred content,soil cap thickness,thickness of each STS layer,and thickness of pure sand layer between the STS mixtures.Furthermore,geogrid layers have been placed at the interfaces of STS and pure sand layers.In addition,the dimensions of geogrid layers and their positions were studied.
2.Materials
2.1.Sand
The grain size distribution of sand is used in this research,as shown in Fig.1.The physico-mechanical properties of the sand are listed in Table 1.

Table 1 Engineering properties of sand used in the current study.
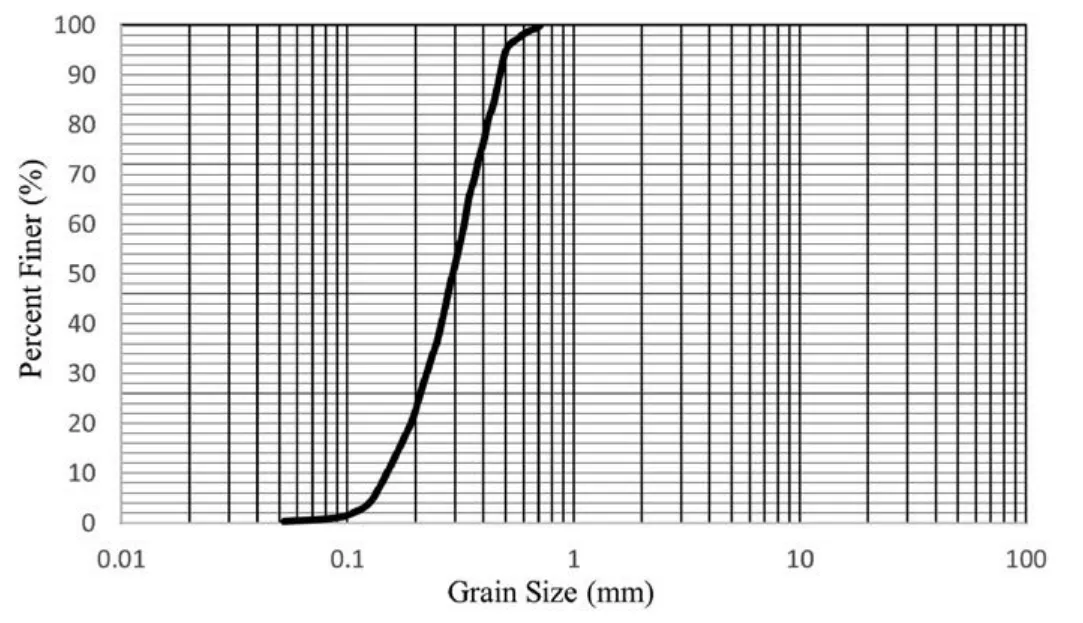
Fig.1.Size distribution of sand.
2.2.Tire shred
In this study,waste tire shreds were cut into rectangular shapes with widths (B) of 2 cm,3 cm,and 4 cm.A special cutter was employed to prepare these specified widths.For 2 cm width shreds,the aspect ratios(i.e.ratio of length to width)were 1,2,3,4,5,and 6.For 3-cm width shreds,the aspect ratios were 1,2,3,4,and 5.For 4-cm width shreds,the aspect ratios were 1,2,3,and 4.Therefore,15 tire shreds with different dimensions were used.Fig.2 shows the shreds with different widths and aspect ratios.The tire shreds adopted in this study are similar to those used by Ghazavi and Amel Sakhi (2005a,2005b).They reported that the tire shreds has a specific gravity of 1.3,failure tensile strength of 1115 kPa,and elasticity modulus of 23.53 MPa.Also,the matrix unit weight in this study is 15.5 kN/m3.The definition of the matrix unit weight is given by Ghazavi and Amel Sakhi(2005a,2005b)and Ghazavi and Kavandi (2022).

Fig.2.Tire shreds with various widths,used in the current study: (a) B=4 cm,(b)B=3 cm,and (c) B=2 cm.
2.3.Geogrid
Biaxial geogrid CE161 made of high-density polyethylene(HDPE) was used in this study (Ahmad et al.,2022).Its properties are given in Table 2.The tensile strength of the geogrid is relatively low,making it a proper choice to study the scale effect on the reinforcing material.

Table 2 Properties of geogrids (Ahmad et al.,2022).
3.Setup and procedure
3.1.Testing equipment
The physical modeling was conducted in a cubic box measuring side length of 1000 mm.The front face of the box was transparent Plexiglas,and other faces were made of steel.The steel footing in the experiments was circular with 30 mm of thickness and 100 mm of diameter.The use of this diameter was due to laboratory limitations,and the use of larger footing diameters can create boundary condition effects.The boundary conditions are negligible when the loading box width is more than 6 times the footing diameter(Yetimoglu et al.,1994).The static loading system consisted of a 2-ton pneumatic jack,a load cell,and two linear variable differential transformers(LVDTs)on both sides of the footing plate.The loading box was inside a rigid frame,and the loading jack was mounted on the same frame.The load applied on the steel plate and its settlement were measured using the load cell and LVDTs.The testing apparatus is shown in Fig.3.
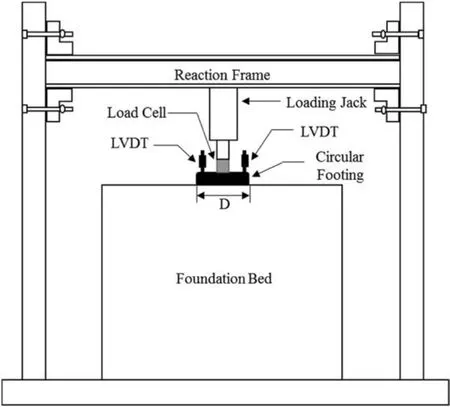
Fig.3.Schematic view of testing apparatus. D is the footing diameter.
3.2.Scale effects
The scale effects should be taken into account for extending the laboratory-scale results to practical cases.Obtaining precise design parameters requires large-scale experiments,which can be expensive and time-consuming.The laboratory limitations make such tests unfeasible.For example,increasing the diameter of the footing can cause boundary condition effects.However,the results of small-scale tests can properly be extended to actual practical scales,albeit they cannot be used directly.The scale factorNis used to compare the laboratory model and the prototype,which can be calculated by
Some physico-mechanical properties are the same for the modeland prototype,including soil unit weight,relative density,internal angle of friction.Therefore,these parameters are not influenced by the scale effects(Gaudin et al.,2007).IfD/D50is above 50 or 100,the scale effects of soil grains and shear bands can be neglected(Taylor,2018),whereD50is the mean grain size of the soil.In this study,D50was 0.3 mm and theDwas 100 mm.Thus,the ratio ofD/D50is 333,and the scale effects of soil grains and shear bands can be ignored.The primary basis of the tire shred’s effect on the footing-bearing capacity is the friction between the soil grain and tire shreds,interlocking effect,and shear band formation.Also,Ghazavi and Amel Sakhi,(2005a,2005b) found similar optimal dimensions for increasing the shear strength parameters of the STS mixtures by conducting CBR and large-scale direct shear tests.The scale factor for the footing modulus of elasticity is defined as 1/N(Dhanya et al.,2019).In this study,a steel plate as the footing was used with an elasticity modulus of 200 GPa,and the elasticity modulus of a real footing (reinforced concrete) is 28 GPa.Thus,Emodel/Eprototypebecomes approximately 7;therefore,a scale factor of 7 was used for this study.According to Wood (2017),the scale effects of bending stiffness should be accounted for to achieve a similar settlement and stress for the laboratory model and prototype.Thus,Eq.(2) is used for the scale factor of stiffness (k) as
where α is 0.5 for sand(wood,2004),and therefore the scale factor for stiffness is√----N;and forN=6-7,the stiffness of the prototype was approximately 2.5 times the stiffness of the laboratory model.
The scale effects of the tensile strength should be considered for geogrid,for which the scale factor isN2for geogrid (Ghazavi and Nazari Afshar,2013;Langhaar,1962).The geogrid used in this study is appropriate,which has a low tensile strength of 6.1 kN/m.ForN=6-7,a geogrid with a tensile strength of more than 200 kN/m can be used;for example,the geogrid that Wulandari andTjandra (2006) employed with a tensile strength of 240 kN/m.Materials with higher tensile strength than geosynthetics and polymers,such as bamboo (Amarnath Hegde,2016;Saha and Mandal,2020),can be employed for geogrid.Therefore,the results of this study could be used for real-scale applications.Table 3 shows the scale relation for parameters involved scale effect in this study.

Table 3 Scale relation for contributing parameters in scale effect analysis.
3.3.Testing procedure and sample preparation
In this research,a matrix unit weight of 15.5 kN/m3was considered for the sand portion in the STS mixtures to compare results for footing load-settlement data corresponding to various shred contents of a certain mixture.It is noted that the matrix unit weight is defined as the sand weight divided by the matrix sand volume (Foose et al.,1996;Ghazavi and Amel Sakhi,2005a,b;Ghazavi and Kavandi,2022).Tire shreds were used in different percentages of 5%,8%,10%,12%,and 15%by weight.For mixing soil and shreds,a small layer of sand(usually between 1 cm and 2 cm)is first poured and the shreds are randomly poured in percentages by weight of each layer.After that,this procedure was repeated to reach a desired thickness for the STS mixture.As an example,Fig.4 shows how the shreds are placed on the sand surface.To achieve an expected density of sand and STS mixtures,an 18-kg hammer with dimensions of 20 cm×20 cm was used.The hammer was dropped from 30 cm height several times to compact the sand and STS mixtures.To achieve the expected and controlled compaction degree,sand layers and sand-shred mixture layers were pounded every 10 cm to reach the prescribed thickness.After preparing the soil bed,a circular steel footing was placed on the soil surface and loaded by a pneumatic jack and load cells.The footing settlement was also recorded by LVDT.
3.4.Testing schedule
In this study,a total of 116 tests were performed,of which 15 tests were repeated under the same conditions to make sure that the results were indicative and repeatable.By observing the results,it was concluded that the differences among these repeated tests were negligible.The primary parameters were footing diameter(D),settlement (S),shred width (B),shred length (L),soil cap thickness(u0),thickness of each STS layer(h),thickness of the pure sand layer between the STS mixtures(u),geogrid width(b),and the number of geogrid reinforcement layer (N).Fig.5 shows the geometry of the foundation and variables while using a single STS layer.
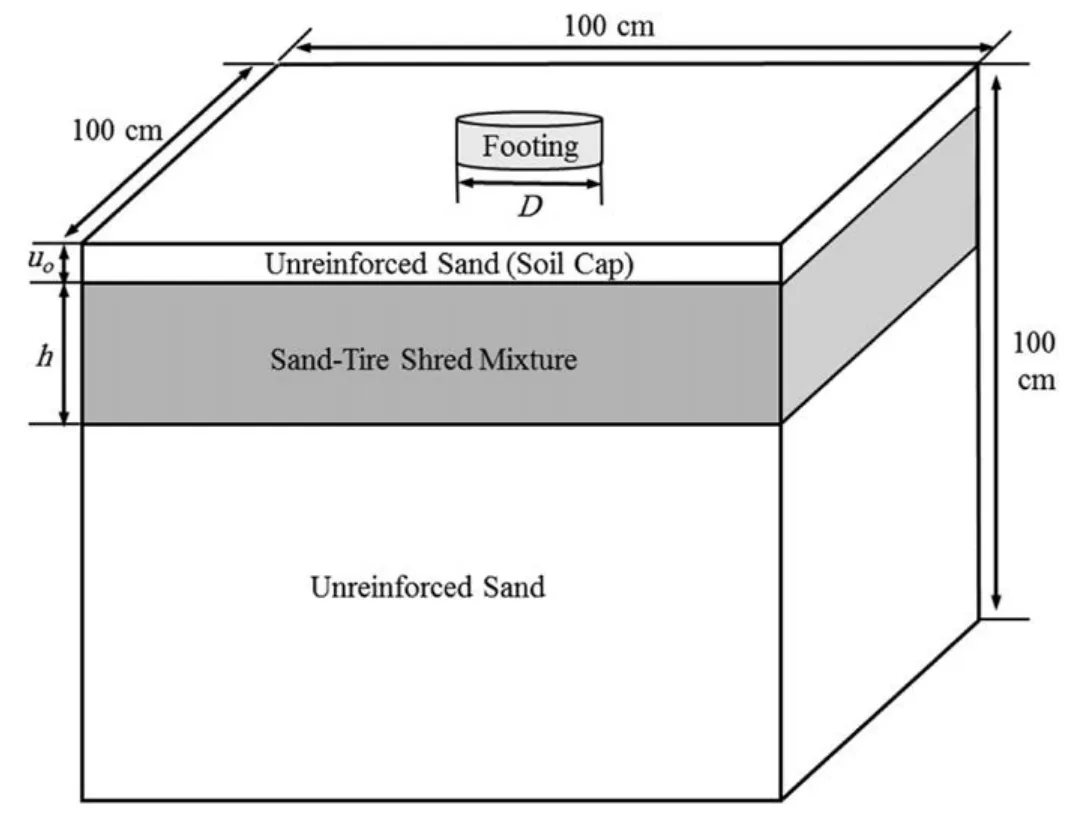
Fig.5.Foundation bed geometry.
Six series of tests,i.e.A,B,C,D,E,and F,were conducted.Details are given in Table 4.Test series A was performed on fully unreinforced sand as the reference tests for comparison of their results with those obtained from reinforced soil tests.The dimensions(aspect ratios) and the optimal shred content in the STS mixtures were determined in test series B.In this series,tire shreds with widths of 2 cm,3 cm,and 4 cm,different aspect ratios,and various shred contents were used.Test series C was performed to determine the optimal soil cap thickness(u0)located beneath the loaded footing.Test series D was carried out to find the optimal thickness of the STS layer (h).Multi-layered STS mixtures were used in test series E to assess the effect of layering and the optimal thickness of the pure sand layer between the mixture layers (u).Finally,test series F was carried out with geogrid layers for sand reinforcement.The variables using multi-layered mixtures and the geogrid placement positions are illustrated in Fig.6.As shown In this figure,the geogrid (I)is placed first,and then for subsequent tests,layers(II),(III),and(IV)are added.The applied pressure-settlement variations are plotted for various cases.Because peak points are not observed in the curves,the intersection tangent method is used to obtain the bearing capacity of the footing (Cerato,2005;Lutenegger and Adams,1998;Trautmann and Kulhawy,1988).
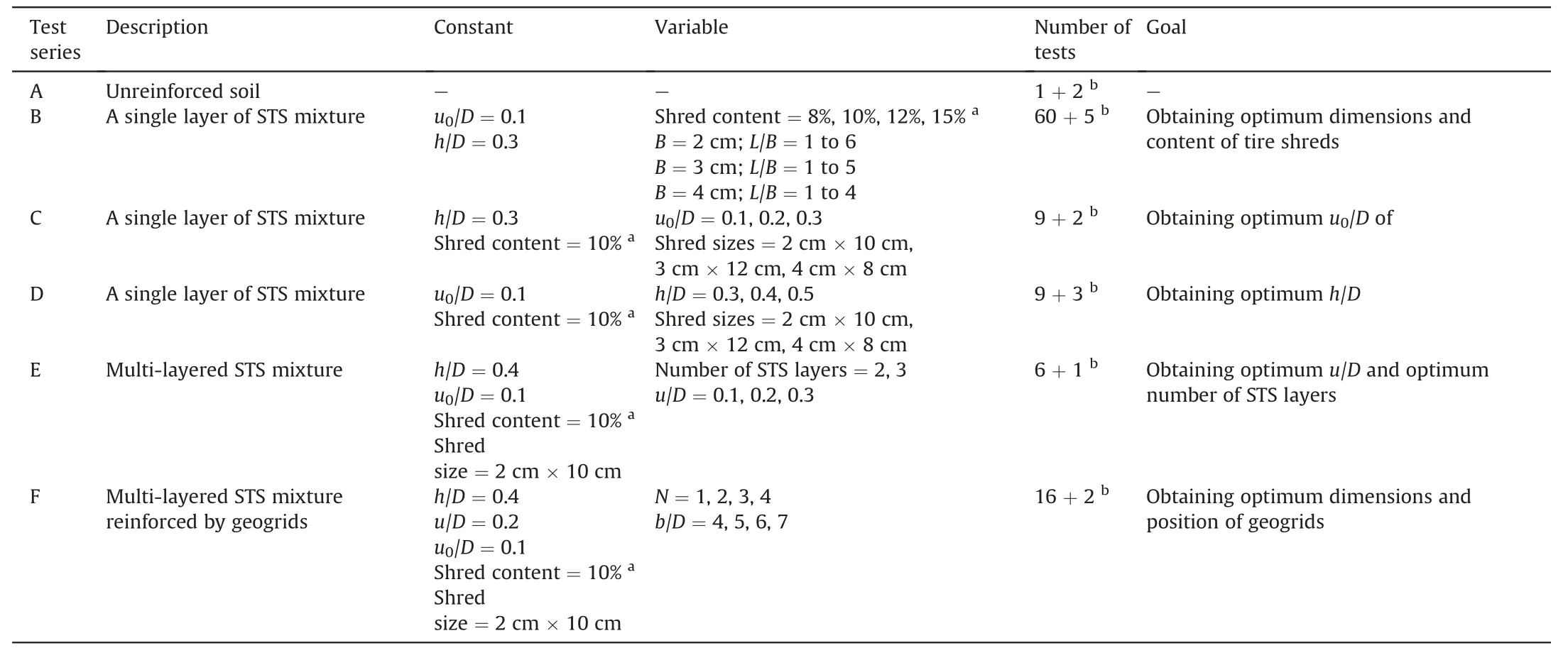
Table 4 List of performed test series.
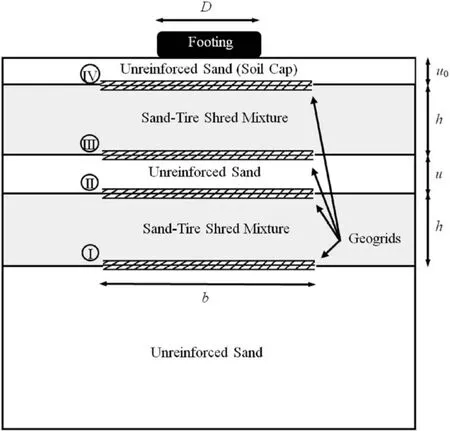
Fig.6.Schematic view for experiment setting and geogrid placement positions(not in scale).
4.Results and discussion
4.1.Optimal shred content and aspect ratio
Test series B comprising 65 tests was performed to determine the optimal tire shred content in the STS mixture and the optimal aspect ratio corresponding to widths of 2 cm,3 cm,and 4 cm for tire shreds.The soil cap thickness(u0)and the STS mixture thickness(h)were assumed to be 0.1Dand 0.3D,respectively,in these tests.The bearing capacity ratio (BCR),defined as the ratio of the bearing capacity of the footing on reinforced soil to that of the footing on unreinforced soil,was employed to compare the results of using different percentages of tire shreds.
TheBCRvariation as a function of tire shred content for 2 cm width shreds is depicted in Fig.7a.As observed,the optimal dimension was 2 cm × 10 cm,the tire shred content in the STS mixture was between 5%and 15%by weight,and the optimal shred content was 10%for 2 cm shred width and aspect ratios of 1,2,3,4,5,and 6.Fig.7b and c shows theBCRvariation versus shred content for 3 cm and 4 cm width shreds,respectively.As seen in Fig.7b and c,the optimal dimensions are 3 cm × 12 cm and 4 cm × 8 cm,respectively,similar to that by Ghazavi and Amel Sakhi (2005a,2005b).Furthermore,the optimal content of the 3 cm and 4 cm shred widths was 10% by weight for all aspect ratios.Using more percentages of tire shreds in the STS mixture than the optimum content,segregation occurs between tire shreds and sand grains,which causes compressibility and increases the footing settlement.Therefore,greater shred contents than 10% by weight in the STS mixture leads to a decrease of footingBCR.
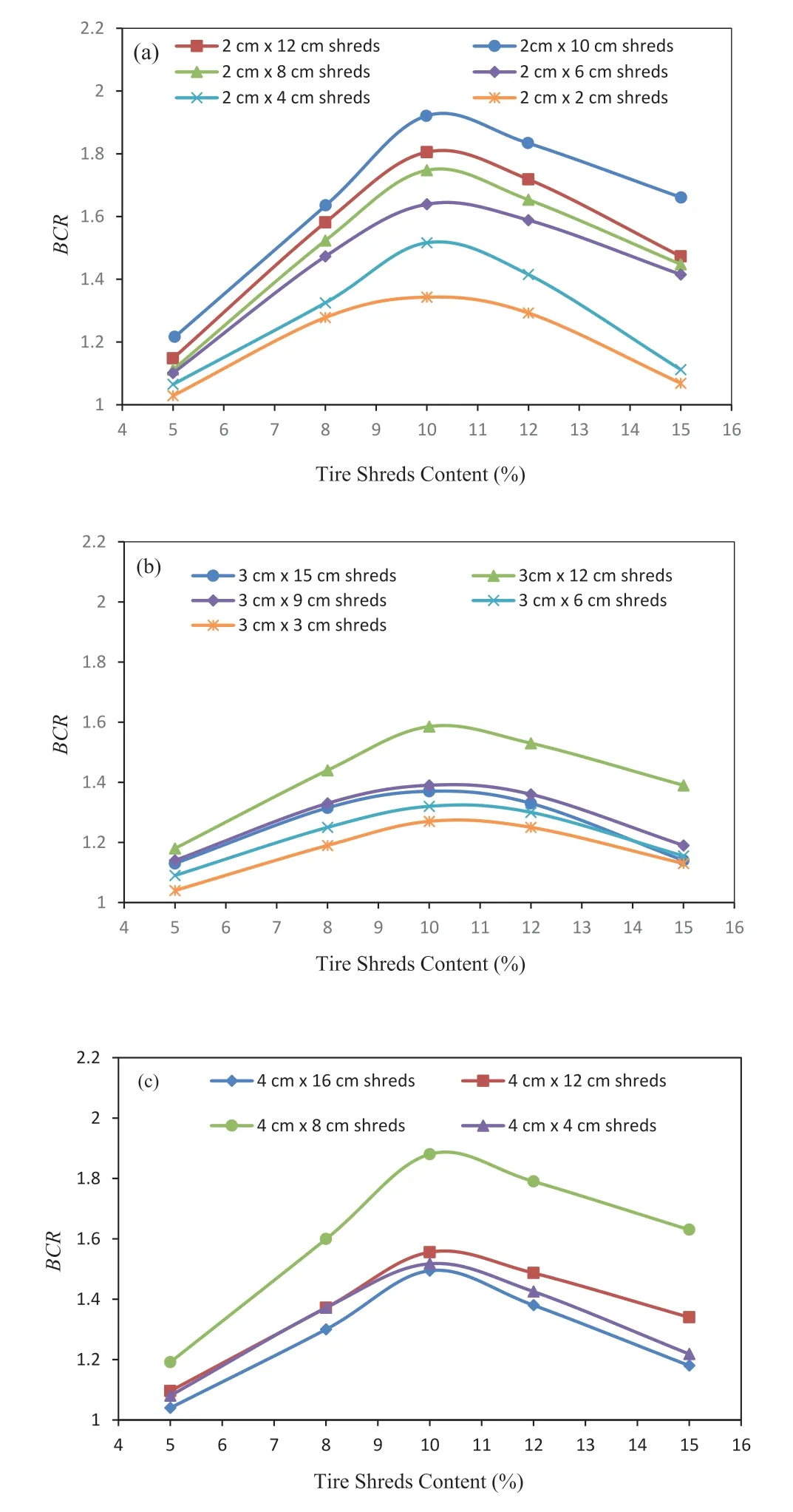
Fig.7.Variation of footing BCR versus tire shred content for shreds with width of (a)2 cm,(b) 3 cm,and (c) 4 cm.
Fig.8 shows a three-dimensional (3D) view of shred width,optimal aspect ratio corresponding to each shred width,and obtainedBCRvalues.In Fig.8,the red line is in the 3D space of coordinates and mapped on two planes(the green line is on the“BCR-(L/B)opt”,and the blue line is on the“B-(L/B)opt”plane.As observed,the greatest footingBCRvalue of 1.91 was achieved for the STS mixture containing 2 cm × 10 cm shreds.For 3 cm and 4 cm tire shred widths,the optimumBCRvalues are 1.88 and 1.58 for 4 cm × 8 and 3 cm × 12 cm shreds,respectively.The increased bearing capacity for the circular footing may be attributed to the soil-tire shred shear interaction.The shear interaction creates a tensile force in tire shreds while they have a low modulus of elasticity.This causes a better interaction between sand grains and shreds.In reality,it suggests that tire shreds deform elastically and experience elongation after loading.Such deformation leads to a much better interaction with sand grains.Furthermore,the sand grains may penetrate slightly into the shred pieces,resulting in mobilization of the friction between the sand and tire shreds as well as interlocking.In this case,an axial load is induced in the tire shreds that can be combined with passive forces caused by creating failure surfaces and makes more resistance of the STS mixture against the applied loading than using pure sand.With increasing loading,gradual formation of failure surfaces occurs,and shreds can function as “anchors,” thereby developing the failure surfaces.In addition,the presence of tire shreds expands the shear local bands and can improve theBCR,as indicated by Ghazavi and Amel Sakhi (2005a,b).

Fig.8.The 3D view of optimum aspect ratio,the width of shred,and BCR variations(red line is in the space coordinate and mapped on the two planes).
It can be concluded that there is only one length for each shred width that provides the maximum bearing capacity of footing,as Ghazavi and Amel Sakhi(2005a,2005b)achieved this result for the shear strength and CBR of the STS mixture.
For shreds shorter than the optimum length,sufficient friction between the shreds and sand was not achieved,also the produced axial load in shreds was reduced.In other words,tire shreds provided a shorter anchored length.Hence,the shorter tire shreds showed a lower increase in footing-bearing capacity.Due to the bending of longer tire shreds than the optimum length under loading,a smaller contact area was obtained between the shred and sand,and thus using the STS mixture will have a smaller increase in the bearing capacity (Ghazavi and Amel Sakhi,2005a).
Ghazavi and Amel Sakhi (2005a,2005b) plotted the optimal aspect ratio(L/B)optfor various shred widths(B)using the CBR and large-scale direct shear tests on STS mixtures:
Since the tire shreds used in the current study are the same as those used by Ghazavi and Amel Sakhi(2005a,2005b),the results for optimal aspect ratios with different widths of shreds were similar.
4.2.Optimal thickness of the soil cap
Bosscher et al.(1997)reported that the best performance of the STS mixture is achieved when a soil cap covers it.They used tire shreds under the highways and the thickness of the soil cap was between 30 cm and 100 cm.In this research,the effect of soil cap thickness (u0) was investigated and its optimal value was determined.To this aim,11 tests(series C)were conducted in which the mixture thickness (h) was 0.3D,and the soil cap thickness (u0)varied between 0.1Dto 0.3D.Mixtures of 10% by weight with 2 cm×10 cm,3 cm×12 cm,and 4 cm×8 cm shreds were used for these tests.Fig.9a-c shows the applied pressure-settlement variations for 2 cm × 10 cm,3 cm × 12 cm,and 4 cm × 8 cm shreds,respectively.As seen,the optimum value for footing-bearing pressure was achieved when the soil cap thickness was 0.1D.
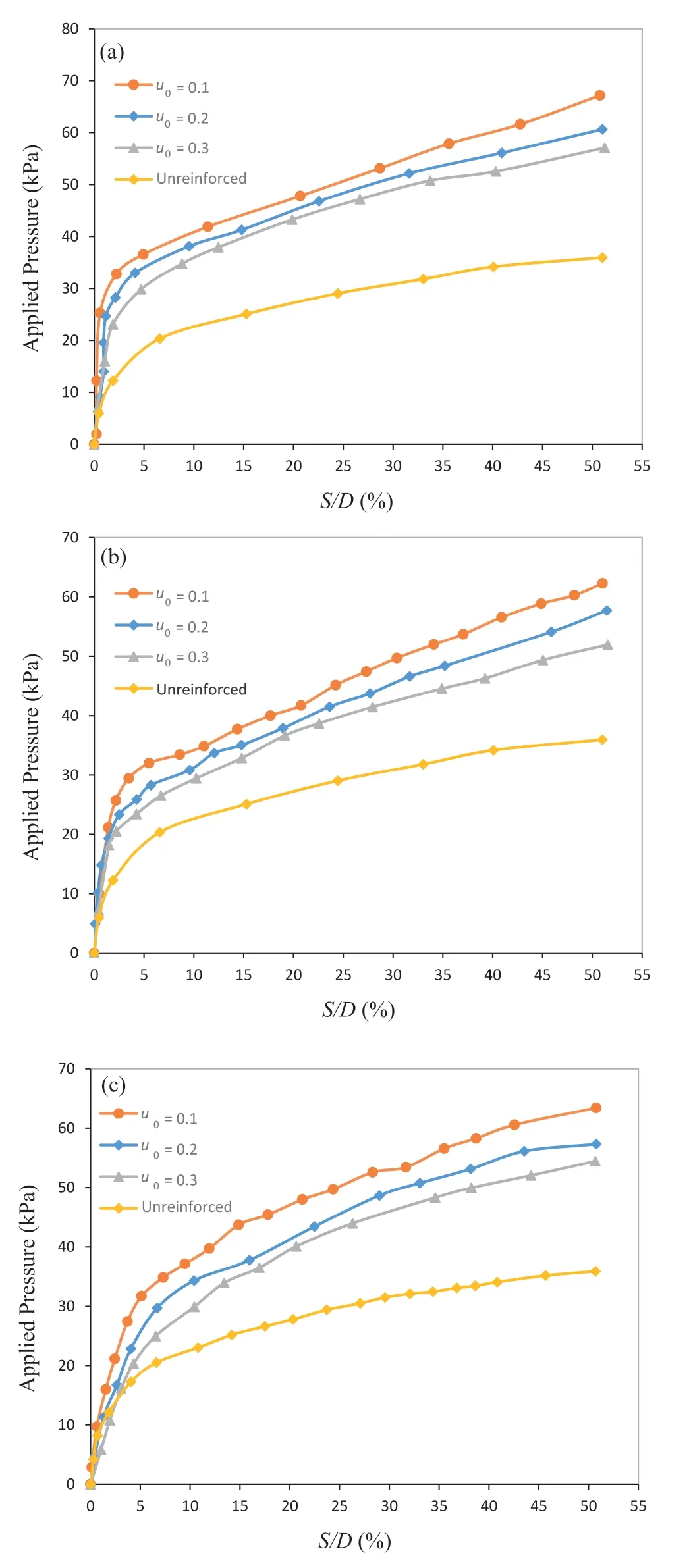
Fig.9.Variation of pressure-settlement ratio for footing on sand-shred with 10%shred by weight and h/D=0.3 for(a)2 cm×10 cm shreds,(b)3 cm×12 cm shreds,and(c)4 cm × 8 cm shreds.
4.3.Optimal thickness of the STS mixtures
The optimal thickness of the STS mixture layer was investigated using 12 tests (series D).In these tests,the shred content was 10%by weight,the soil cap thickness was 0.1D,and optimal dimensions of each shred width(2 cm×10 cm,3 cm×12 cm,and 4 cm×8 cm)were used.Three different thicknesses of 0.3D,0.4D,and 0.5Dwere considered for the mixture layer.Fig.10a-c demonstrates the applied pressure-settlement curve for the three shred dimensions.In all cases,the optimal thickness of the mixture layer was 0.4D.
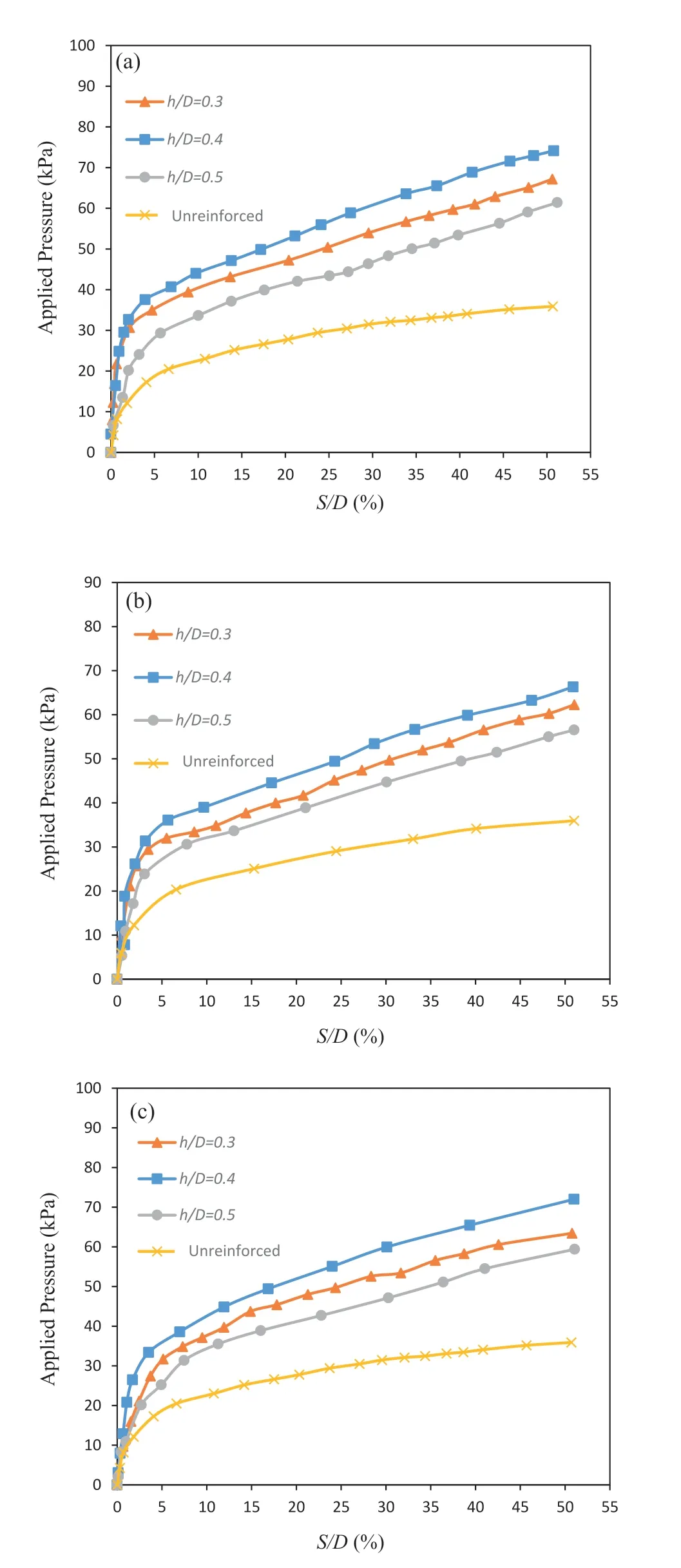
Fig.10.Variation of applied pressure-settlement ratio with 10% by weight shreds and u0/D=0.3 for(a)2 cm×10 cm shreds,(b)3 cm×12 cm shreds,and(c)4 cm×8 cm shreds.
TheBCRvariation as a function ofh/Dis depicted in Fig.11 for optimal dimensions of each width of tire shreds (2 cm × 10 cm,3 cm × 12 cm,and 4 cm × 8 cm).Therefore,the maximumBCRresulting from a single layer of the STS mixture was obtained by 2.38 where the shred width was 2 cm,the aspect ratio was 5,the soil cap thickness was 0.1Dand the STS mixture thickness was 0.4D.
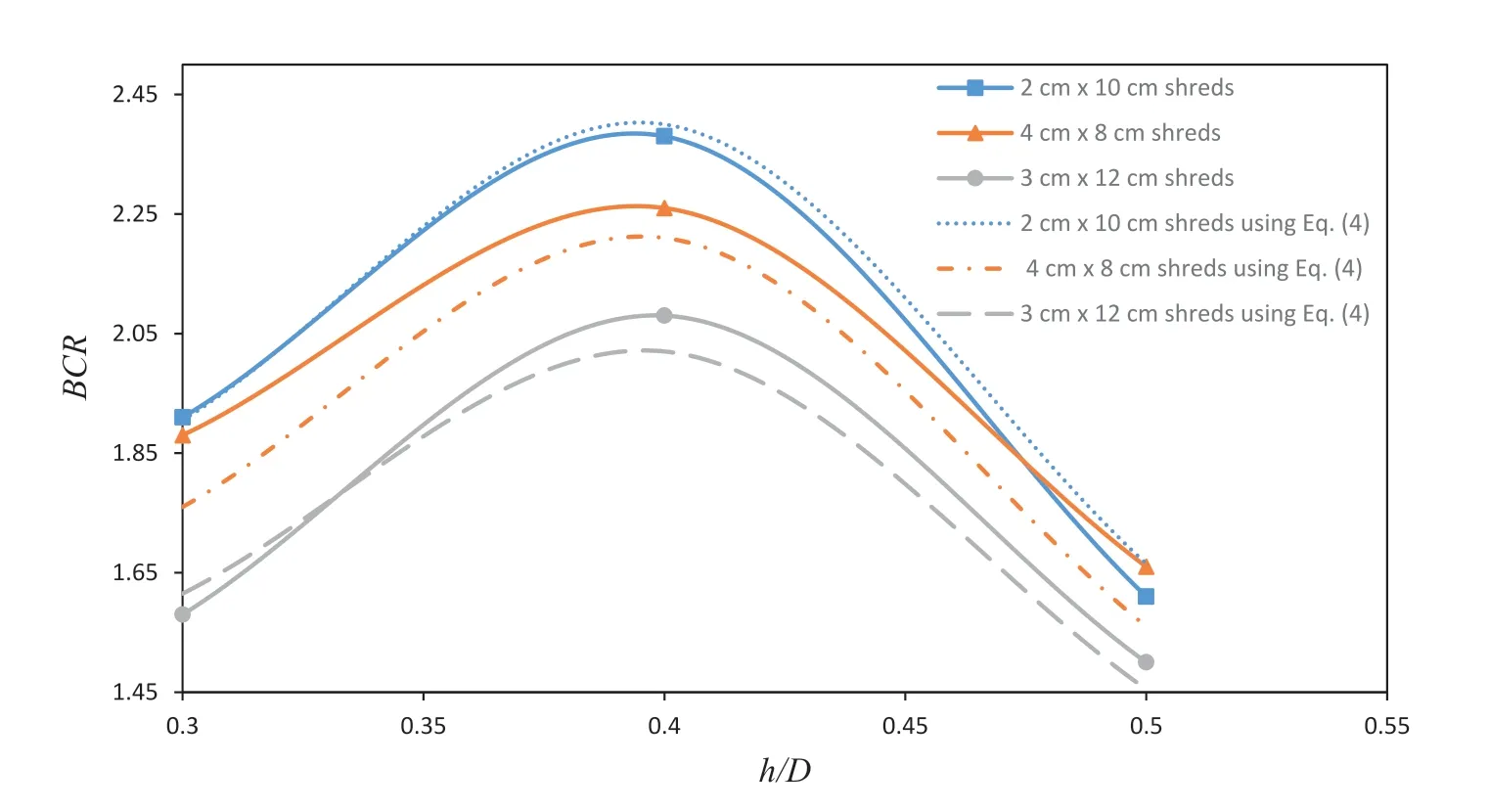
Fig.11.Variation of measured and predicted footing BCR values with different thicknesses of the STS mixture (h/D) with the shred content of 10% by weight.
By investigating the variation of pressure-settlement for footing on a layer of sand-shred mixture (using 10% by weight shreds
mixing with sand and optimum thickness of soil cap that is 0.1D),we have
whereBis the shred width for various (L/B)opt(B=2 for 2 cm × 10 cm shreds,B=3 for 3 cm × 12 cm shreds,B=4 for 4 cm×8 cm shreds).Using other widths of the shreds and various thicknesses of STS mixture,it is possible to find the(L/B)optfrom Eq.(3),then using Eqs.(4)-(7) to calculate theBCR.Fig.11 shows the difference between the curve obtained from the results of laboratory tests and the mathematical calculation of Eqs.(4)-(7).In this regard,it is possible to use different thicknesses of STS mixture for different widths of shreds,which is helpful for laboratory tests and real projects.
For mixture layers thicker than 0.4D,the footing-bearing pressure was lower than the optimum,since increasing the thickness of this layer more than the optimum value reduces the bed elasticity modulus.Thus,it makes the foundation bed more flexible and the footing experiences more settlement.Furthermore,the layer of the STS mixture acts like a shear and bending beam;by applying pressure,bending occurs in this layer and the lower part of the layer experiences tension.Indeed,tire shreds can tolerate this tension.Furthermore,the tire shreds in the mixture can propagate the stress laterally rather than vertically,as indicated by Fazeli Dehkordi et al.(2021) for footings on geosynthetic-reinforced soil.When increasing the thickness of the layer gradually,due to the low elastic modulus of the tire shreds,the stiffness of the layer decreases and it offers a lowerBCRcompared to the optimum value.The solution is to use multi-layer for the STS mixture,which will be investigated in the subsequent sections.
4.4.Multi-layered STS mixtures
Test series E (seven tests) was performed to evaluate the effect of multi-layered STS mixtures.The pressure and settlement were measured for two and three layers of the mixture in these tests.A layer of pure sand with thicknesses of 0.1D,0.2D,and 0.3Dwas used between the mixture layers.Fig.12 plots the footingBCRas a function of soil cap thickness where 2 cm×10 cm shreds with 10%by weight were used in a 0.4Dthick STS mixture.As Fig.12 shows,the footing performance was improved for two and three layers of the STS mixture compared to the single layer,and the optimal thickness of the pure sand layer between the tire-reinforced layers(u) was 0.2D.
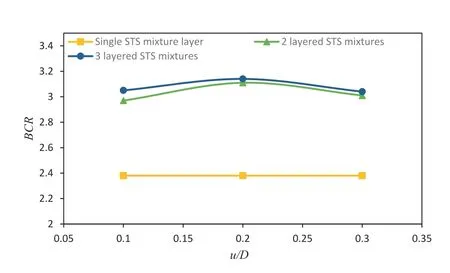
Fig.12.Variation of footing BCR with different thicknesses of pure sand layer between STS layers (u/D) with 2 cm × 10 cm shreds and content of 10% by weight.
Concerning the practical and economic conditions,the best choice is to use the limited number of layers of STS mixture (two layers are assumed in this study),but there is little difference between the increased strength provided by two and three layers of STS mixtures.Furthermore,increasing the STS layers can cause footing rotation,as observed by the authors.Therefore,it can be concluded that the effective depth of the footing and applied loading was in the range of 1-1.5D.Using two-layered STS mixture(optimum mixtures with a thickness of 0.4Dand 10%by weight of 2 cm × 10 cm shreds),a 0.2Dthick pure sand layer located in between the STS mixtures can increase the footingBCRby 3.11.
4.5.Geogrid reinforcement effects
Test series F consisting of 18 tests was carried out to investigate the effect,optimal positions and width of geogrid layers.Two STS mixture layers were used,as described in Section 4.4.There were 1,2,3,and 4 geogrid layers placed at the interfaces of the STS mixture and pure sand layers.Fig.13 illustrates the footingBCRvariation versus the number of geogrid layers with widths of 4Dto 7D.As observed in Fig.13,the optimal width of the geogrid was 5Din all tests and this result is compatible with previous experimental and numerical research (Rostami and Ghazavi,2015;Useche-Infante et al.,2022).As observed in Fig.13,geogrid layer IV (the uppermost interface of the STS mixture and pure sand layer) did not contribute to the variation of the footing-bearing capacity because it was not within the failure zone.This is consistent with the results from Useche-Infante et al.(2022).Therefore,the best load-carrying characteristic for footing is achieved when two mixtures of STS(optimum STS mixture with the thickness of 0.4Dand 10% by weight of 2 cm × 10 cm shreds) are reinforced by three layers of geogrid (I),(II),and (III).The geogrid layers were at the bottom of the interfaces of the STS mixtures and pure sand layers,which led to the highest footingBCRof about 4.
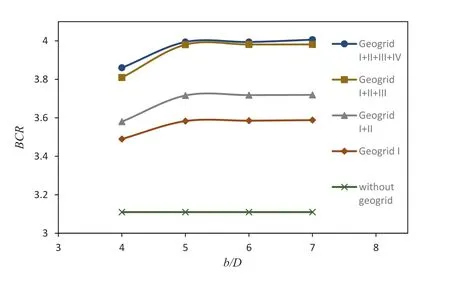
Fig.13.Variation of footing BCR versus geogrid width (b/D) in two layers of STS mixture (h/D=0.4, u/D=0.2,and shred contents=10% by weight).
Geogrid layers placed at the interfaces of STS mixtures and pure sand layers could significantly increase the footing-bearing capacity since geogrid restrains sand grains and rubber against lateral movement and causes a better interaction for STS.Due to the geogrid membrane,a horizontal passive component is created that either prevents pull-out or spreads the applied load laterally rather than vertically(Beyranvand et al.,2021;Fazeli Dehkordi et al.,2021;Hegde and Roy,2018;Shadmand et al.,2018).Furthermore,it seems that when the geogrid reinforces the mixture substrate,the shreds in contact with geogrid layers create a slightly passive horizontal force as well(Beyranvand et al.,2022).All of these lead to increase of the footing-bearing capacity.
5.Conclusion
This study investigated the effect of different sizes of tire shreds,their content in single or multi-layered STS mixtures,and also the effect of geogrid used at the interfaces of STS and pure sand layers,on improving the circular footing load-carrying capacity by performing laboratory tests.Based on the chosen materials,footing geometry,and testing procedure used in the current study,the main conclusions are drawn as follows:
(1) For the tire shreds with sizes of 2 cm×10 cm,4 cm×12 cm,and 3 cm×12 cm,the optimal aspect ratios were about 5,4,and 2 for 2 cm,3 cm,and 4 cm shred widths,respectively.The optimal content of the tire shreds in the STS layer was 10% by weight,regardless of tire shred size.
(2) The optimum thickness of the soil cap was obtained by 0.1D.Thicker caps decrease the footing-bearing pressure.The optimum thickness of STS layer to achieve the maximum bearing capacity was 0.4Dand using a single layer of STS mixture improves the footingBCRvalue by about 2.38,when considering the optimum values of tire shreds content,shred width,aspect ratio,thickness of soil cap and STS mixture.
(3) Multi-layered STS mixtures can improve the footingBCRby about 3.11.This increase in the bearing capacity was obtained using the limited number of STS mixtures(two layers in this study),considering the optimum values of STS and pure sand layers thickness,tire shred content,shred width,and aspect ratio.Using more than two layers of STS mixture cannot increase the bearing capacity of the footing.
(4) The use of geogrid layers reinforcing the STS mixtures also significantly improved the supported footingBCR.The optimal dimension of the geogrid in this study for reinforcing the STS mixtures was 5D.By increasing the width of geogrids,there is no improvement in bearing characteristics.
(5) The greatest footingBCRvalue was achieved using two STS mixtures when three layers of geogrid were placed at the interfaces of the STS mixture and pure sand.Increasing the bearing capacity of the footing was not considerable when geogrid was placed at the uppermost interface(STS mixture and soil cap interface).
Generally,using this reinforcing system is suitable for loose sand.The use of geogrid layers reinforcing multi-layered tire-shred mixtures leads to a significant increase in the footing-bearing capacity,in addition to the use of tire shreds for environmental consideration purposes.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
杂志排行
Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Using deep neural networks coupled with principal component analysis for ore production forecasting at open-pit mines
- Sliding behaviors of the trapezoidal roof rock block under a lateral dynamic disturbance
- Real-time arrival picking of rock microfracture signals based on convolutional-recurrent neural network and its engineering application
- Failure characterization of fully grouted rock bolts under triaxial testing
- Nonlinear constitutive models of rock structural plane and their applications
- Mechanical behaviors of backfill-rock composites:Physical shear test and back-analysis
