基于分区和滑动时间窗策略的配电网线路参数辨识
2024-03-24李晨涛欧颖雅季天瑶张禄亮
李晨涛,欧颖雅,季天瑶,张禄亮
(华南理工大学电力学院,广东广州 510006)
0 引言
配电网是电力系统不可或缺的重要组成部分。电网的众多应用包括最优潮流计算、故障定位以及状态估计等,都需要电网准确的线路参数[1-3]。但天气、运行等不确定性导致线路参数总是存在一定的偏差。为确保这些应用能表现最佳性能并保障电网稳定,需要对线路进行精确参数辨识。相比输电网,配电网没有足够的冗余数据并且复杂的拓扑使配电网参数辨识任务比输电网更具挑战性;分布式电源让配电线路阻抗辨识也面临新的巨大挑战[4]。
目前,许多学者在国内外进行了配电网线路参数辨识研究,主要分为使用同步测量相角装置(Phasor Measurement Unit,PMU)或微型同步测量相角装置(Micro Phasor Measurement Unit,μPMU)的同步测量方法和使用非同步测量的非同步测量方法。文献[5]通过PMU 测量数据运用抗差最小二乘法辨识参数。文献[6]基于测量误差建立误差-变量模型,并用最大似然估计进行求解。文献[7]基于μPMU 数据分析推算差值来计算得到线路参数。文献[8-10]结合同步测量和非同步测量进行线路参数辨识。尽管这些研究都依赖于PMU 或μPMU 并要求全节点部署,但由于PMU 价格昂贵和通信条件受限,PMU 的实际部署仅限于配电网的少数区域,因此实际应用受到限制[11]。
使用非同步数据的辨识方法提升了参数辨识适用性。文献[12]利用末端智能电表数据进行拓扑和参数的联合辨识,适用于隐节点度大于3 的网络。文献[13]建立了两阶段辨识模型,使用牛顿-拉夫逊法求解线路参数,但结果受数据选择影响。文献[14]在考虑了测量误差的情况下进行了参数辨识。文献[15]考虑了在数据缺失情况下的参数辨识。文献[16]使用逆潮流方程对线路参数进行辨识。文献[17]通过忽略功率中的二阶项,提出了线性解耦潮流(Linear Coupled Power Flow,LC-PF)模型,将电压与节点功率线性化,当电压和功率误差不大时,该LC-PF 模型能够准确反应电压与节点功率的关系。
目前,关于拓扑识别的方法已经比较成熟,文献[18-23]对配电网拓扑进行了准确辨识。为提高线路参数辨识的准确性,本文在假设已知配电网准确拓扑的前提下,基于智能电表所测得数据,使用LC-PF 模型[17]对配电网线路参数进行初始辨识;然后将辨识问题定义为一个最小二乘问题,将线路参数和相角设定为决策变量,利用高斯-牛顿法[24]对线路参数进行精确求解。
1 配电网线路参数辨识框架
本文旨在使用智能电表所提供的量测数据,对线路参数进行准确辨识,配电网线路参数辨识的框架如图1 所示。在已知配电网拓扑的基础上,初始辨识阶段使用LC-PF 模型来识别节点阻抗矩阵的实虚部,并通过降噪和对称处理获得线路初始参数。为提升精确辨识阶段的效率和准确性,将网络分区并应用高斯-牛顿法在不同时间窗内连续辨识。记录并更新辨识过程中的最优值并将其作为下一时间窗的初值,辨识结束后进行离群值检测以排除异常数据,以准确得出线路参数。
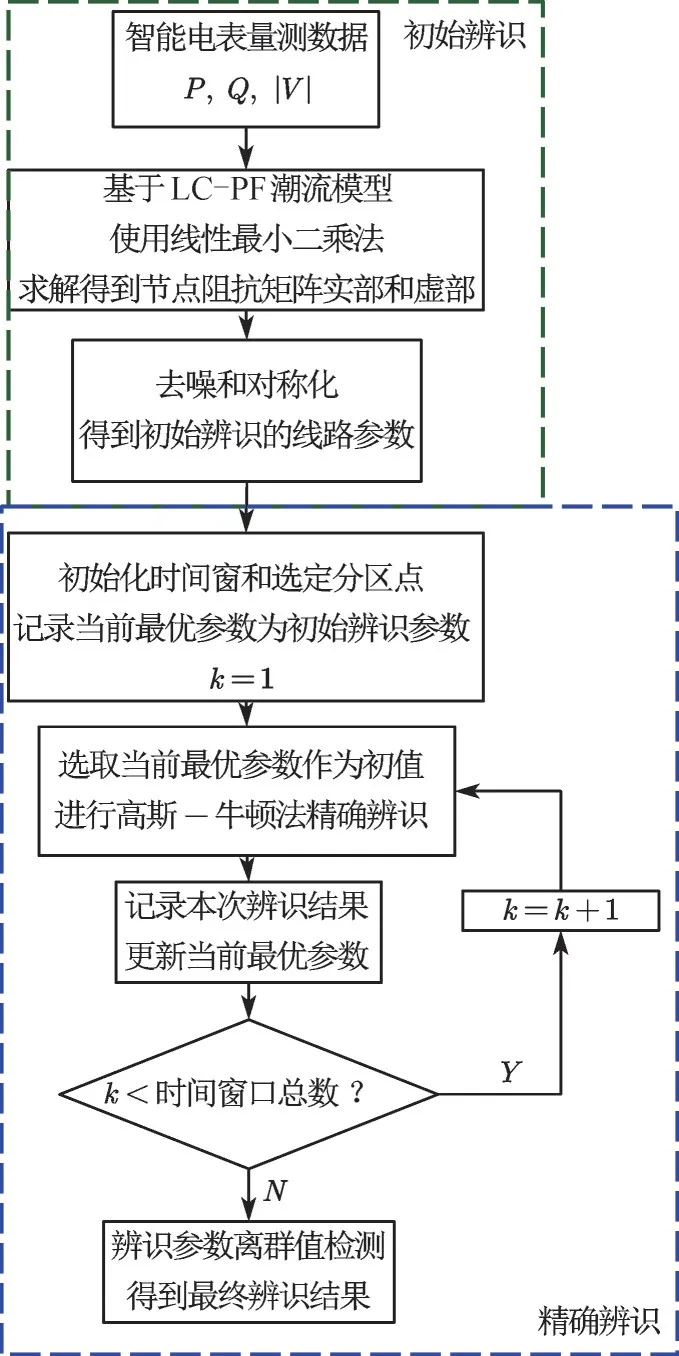
图1 线路参数辨识框架Fig.1 Framework for line parameter identification
图1 中,P,Q和|V|分别为节点有功、无功功率及电压幅值,k为当前时间窗口数。
2 基于数据驱动的配电网线路参数辨识
2.1 基于LC-PF模型的线路参数初始辨识
一个含N个节点的配电网可以用图论中的一个图G来描述,图G可以表示为:
式中:V为配电网的节点集;E为配电网的支路集。
eij为节点i和j之间连通情况,当节点i和j之间有支路直接连接时eij=1,否则eij=0。将潮流公式线性化,可得到LC-PF 模型[21]:
式中:|V|,θ,P和Q分别为节点电压幅值向量、相角向量、有功和无功功率向量,其中,|V|=,θx,px和qx分别为节点x的电压幅值、相角、有功和无功功率,x∈V;Z为配电网的节点阻抗矩阵。
式(2)中节点电压幅值与功率向量线性相关。已知|V|,P和Q,就能解出节点阻抗的实部和虚部,进而得到线路参数的初始辨识值。使用高冗余度数据集进行回归分析以确保线性最小二乘法稳定性,减少数据误差影响。假设用t组数据进行线性回归,且该时间内拓扑和线路参数未发生变化,则:
使用线性最小二乘法求解节点阻抗矩阵:
节点阻抗矩阵是满矩阵,故[R e(Z) Im(Z)]也是满矩阵。这相比直接解稀疏的节点导纳矩阵可减少过拟合,增加求解精度。获得节点阻抗矩阵后,求逆得到节点导纳矩阵,并进行去噪与对称化以确保对称性和符合拓扑,以得到线路的初始参数:
式中:Yinitial#为对称化处理后的节点导纳矩阵;Yinitial为初始辨识得到的节点导纳矩阵。
2.2 使用高斯-牛顿法进行精确辨识
由于智能电表无法提供相角信息,线路参数和相角需作为变量识别并构建辨识模型。
潮流量测数据可以表示为节点电压相位角、电压幅值大小和线路参数的函数,如式(8)所示:
式中:PQt0为t0组潮流测量值向量,PQt0∈ℝ2Nt0;h(v,u)为潮流计算函数向量,h(v,u)∈ℝ2Nt0;v为t0组数据的相位角、每条线路的电导和电纳,;u为t0组电压幅值
为准确辨识线路参数,需得到1 组v使潮流测量值残差平方和最小化,于是参数辨识问题可描述为:
式(9)为一个最小二乘问题,本文使用高斯-牛顿法[24]进行求解,其修正迭代可表示为:
式中:Jk=∂h/∂vk为h第k次迭代时的雅可比矩阵。
式(10)中存在求逆,当t0较大时,求解过慢,在精确辨识中应选择适当的数据集进行求解。假定有t0组数据的负荷处于不同情况,则式(9)有2Nt0个独立测量值,其中(N-1)t0个电压相位角和2m个线路参数将作为未知数,要得到唯一可行解需要满足:
同时还应保证一定的冗余度,多选几组数据进行求解,t0值一般选择5~10。
为确保快速稳定迭代,本文采用文献[13]求伪潮流方法,使用式(3)直接解相角,提高计算速度。
3 滑动时间窗和网络分区策略
在精确辨识阶段,仅用部分数据可能导致辨识不准确。随着配电网节点增加,雅可比矩阵的维度和求逆复杂度上升,影响辨识效率。本文利用滑动时间窗减小不恰当数据选取的影响,并通过分区策略减小雅可比矩阵维度,以缩短计算时间并提升辨识效率。
3.1 滑动时间窗策略
假设每个时间窗大小为t0,共有t个时刻的量测数据,t0⊂t。如图2 所示,为更充分利用数据,固定时间窗大小为t0,在当前时间窗内进行精确辨识后,时间窗有重叠的向后移动,直至数据结束,共有n=t-t0+1 个时间窗口数。最后综合所有时间窗的结果得到最终的辨识参数。

图2 时间窗示意图Fig.2 Schematic diagram of time window
3.2 网络分区
本文借鉴基于马尔科夫链和概率图模型中条件独立性的节点解耦的分区方法[23],在每次精确辨识中实现对各个子区域的独立辨识,提高辨识的效率。
文献[25]指出,在电力系统状态条件独立时,可进行网络解耦分区。若已知电压幅值,则节点功率与邻近线路的电导电纳及相邻节点和自身相角相关。故已知节点状态时,该节点可用于网络的解耦和分区。
假设某个节点的状态已知,将其作为分区点后对网络进行解耦分区,分别辨识每个区域的线路参数和相角。在每个区域内构建出该区域的雅可比矩阵,需注意,分区点的功率同时受不同区域参数的影响,分区点的功率不应该参与式(10)的迭代过程,构建雅可比矩阵时不应考虑分区点的功率;然后利用式(10)求出每个区域内的线路参数和相角,完成精确辨识。
如图3 所示是一个8 节点系统,当节点5 的状态已知时,以节点5 作为分区点,将8 节点系统划分为区域1 和区域2。节点5 作为分区点,其功率不作为参数带入式(10),θ5作为参数带入区域1 的精确辨识迭代过程;虽然在区域2 中,θ5也会影响p6和q6,但因θ5在区域1 内计算得到,所以在区域2 内将节点5 看作该区域的平衡节点进行精确辨识。在区域1 和2 的雅可比矩阵J1=∂h1/∂v1和J2=∂h2/∂v2中,h1,v1,h2和v2的表达式分别为式(12)、式(13)、式(14)和式(15)所示;

图3 8节点系统分区示意图Fig.3 Schematic diagram of 8-bus system partitioning
式中:h1和h2分别为分区计算时的区域1 和2 中的潮流向量;v1和v2分别为分区计算时的区域1 和2 中的相位角和每条线路的电导和电纳向量。
利用高斯-牛顿法在2 个区域分别迭代求解线路参数和相角值。由于分区点的功率未参与精确辨识,分区点数量不宜多。本文分区点选取基于:(1)优先T 型节点,增加区域数减少分区点;(2)平衡各区域节点数,降低雅可比矩阵阶数简化计算。
3.3 精确辨识初始值选取
2.2 节使用高斯-牛顿法进行精确辨识时,采用初始辨识参数作迭代初值及全局最优参数。通过比较潮流偏差以更新全局最优参数,较小潮流偏差的当前参数更新为新的全局最优,并用作下一时间窗迭代初值。此过程持续至最后一个时间窗,优化迭代初值以提升辨识准确度和加快迭代速度。
3.4 离群值检测
假设线路参数在辨识期间不变。若坏数据导致某时间窗参数与其他辨识结果偏离,进行离群检测以排除错误辨识。对电导电纳参数执行离群值检测,定义离群值为超出3 倍中位数绝对偏差M的数值:
式中:X为进行离群值检测的向量;median(X)为向量X的中位数;erfcinv 为逆补余误差函数。
检测到线路电导和电纳参数的离群值后,将该离群值删除,对其余时间窗下辨识的参数求平均值后,得到最终的参数辨识结果,以减少数据不良的影响。
4 算例分析
本文在IEEE 33 节点[24]和PG&E 69 节点[25]系统中对所提出的线路参数辨识方法使用Matlab 进行了仿真验证,并在不同情形下进行了方法性能测试。
本文负荷数据使用文献[13]中的爱尔兰用户数据,并对数据进行相同处理,得到每隔15 min 采样1 次的负荷功率数据。
IEEE 33 节点和PG&E 69 节点系统拓扑如图4和5 所示。33 节点系统中基于节点13 分为3 个区,使用24 小时电表数据,共96 点。69 节点系统按节点3,34 和58 分为6 个区,使用48 小时数据,共192点。为了提高计算效率,本文t0的大小选择为5。

图4 IEEE 33节点系统分区示意图Fig.4 Schematic diagram of IEEE 33-bus system partitioning
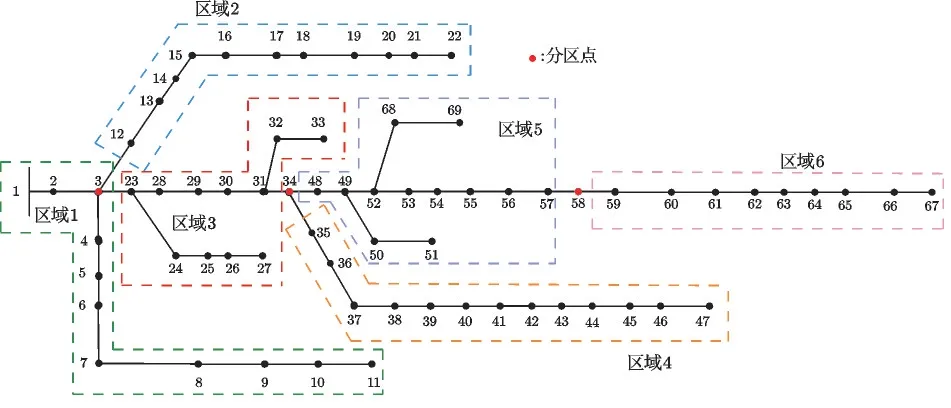
图5 PG&E 69节点系统分区示意图Fig.5 Schematic diagram of PG&E 69-bus system partitioning
本文使用绝对百分比均值误差(Mean Absolute Percentage Error,MAPE)(量值为EMAP)来评估此参数辨识方法的总体辨识性能,使用相对误差(Relative Error,RE)(量值为ER)来评估每条线路的参数辨识结果,如式(17)所示:
式中:Ki,real为第i个参数的真实值;为在第j个时间窗下第i个参数的参数辨识值;ERi为第i个参数的相对误差。
4.1 典型案例分析
为了符合真实的测量情况,在33 节点系统设置0.5%功率误差和0.05%电压幅值误差,线路初始辨识的电导MAPE 值为7.24%,电纳MAPE 值为9.19%,接近真实参数。这为后续精准辨识提供好的初始值,以规避陷入局部最优,其辨识结果如图6(a)和图6(b)所示。经过初始辨识,在92 个时间窗下进行精确辨识,进行离群值检测后,精确辨识的结果为:电导MAPE 为0.44%,电纳MAPE 为0.61%,辨识的结果如图6(c)和图6(d)所示,辨识的结果非常接近真实值,在一定程度上体现了本方法的有效性。在i5-1135G7 CPU 和16GB RAM 的计算机中,经13.04 s 后完成辨识。
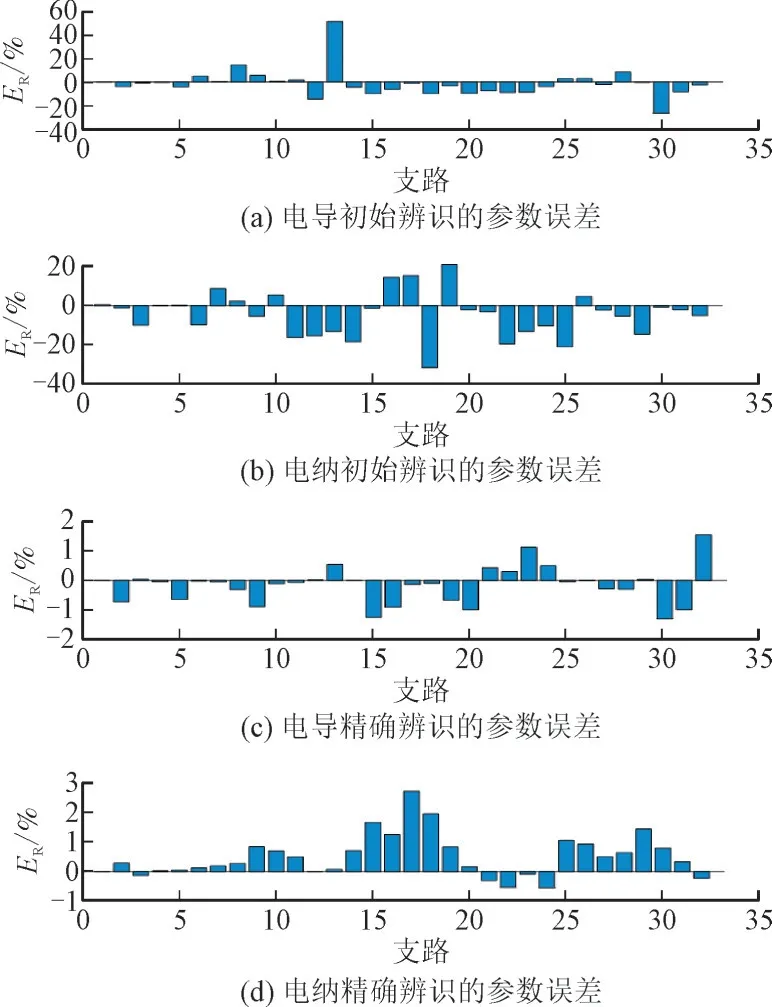
图6 线路参数辨识误差Fig.6 Diagram showing errors of line parameter identification
4.2 功率噪声的影响
实际测量的量测误差通常是测量范围的0.5%~1%。为测试不同噪声水平下线路参数辨识的准确性,电压误差定为0.05%,功率误差介于0.1%至2%。在每种误差和两个系统中进行了50 次辨识实验,结果见表1。参数辨识精度随功率误差升高而降低,但在误差较小时相对准确。即使误差增至2%,辨识精度在两系统中依旧较高,显示出该方法的鲁棒性。
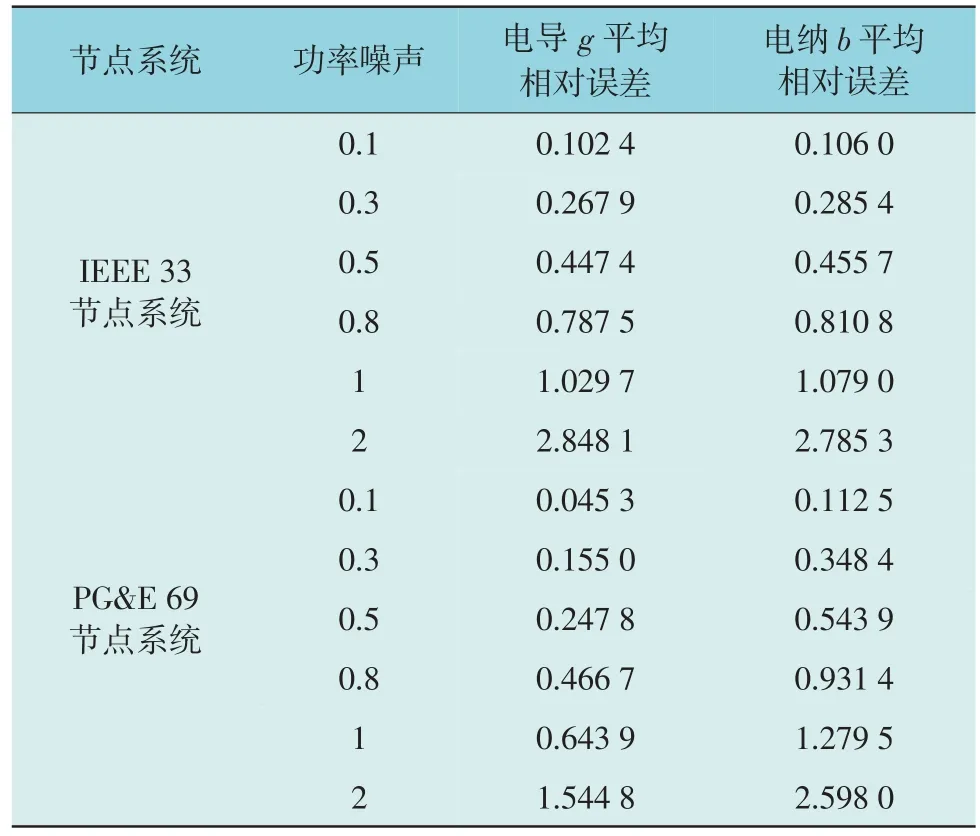
表1 不同功率噪声下线路参数平均相对误差Table 1 Mean relative errors of line parameters with different power noise %
4.3 分布式电源的影响
为评估分布式电源接入对参数辨识的影响,本文在0.5%功率误差和0.05%电压幅值误差下测试了光伏并网对所提方法的影响。33 节点系统的节点6 和节点25,69 节点系统的节点22,节点47 和节点67 接入光伏后,进行了不同渗透率下的50 次辨识,结果见表2。光伏渗透率提高,参数辨识误差几乎不变,表明本方法在具有分布式电源的配电网中具有一定可行性。
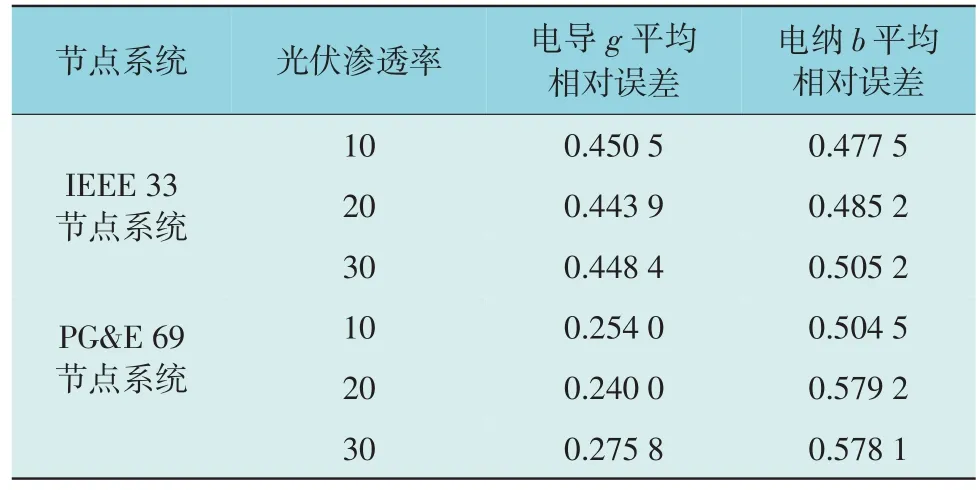
表2 不同光伏渗透率下线路参数平均相对误差Table 2 Mean relative errors of line parameters with different photovoltaic penetration %
4.4 时间窗和分区的影响
本文设置了5,10,15 的时间窗口和有无分区条件,在两个系统中测试辨识效果,结果展示在表3、图7 中。表3 表明,时间窗增大减效了参数辨识误差,但增加了计算量和辨识时间;无分区情况下的平均辨识误差小于分区情况,但耗时更长。图7显示,大时间窗改善了某些线路的辨识结果,但也存在某些线路辨识结果变差。总体上,增大时间窗提升了准确性但也加重了计算负担;而分区则缩短了辨识时间,对结果的影响较小。需综合考虑精度与时间,选择合适的时间窗和分区策略。

表3 不同时间窗和分区下线路参数平均相对误差Table 3 Mean relative errors of line parameters with different time windows and partitions

图7 分区时不同时间窗下线路参数辨识误差Fig.7 Line parameter identification errors with different time windows during partitioning
4.5 分区点数量的影响
在分区过程中,未使用分区点功率可能会影响线路参数辨识。本文测试了在不同分区点数量下两节点系统参数辨识的结果,如表4 所示。分区点增加使相对误差增大,因为一部分数据未被使用,不利于数据驱动的辨识方法。因此,分区点应遵循3.2 节提出的选择原则,以避免过多分区点对辨识结果造成影响。
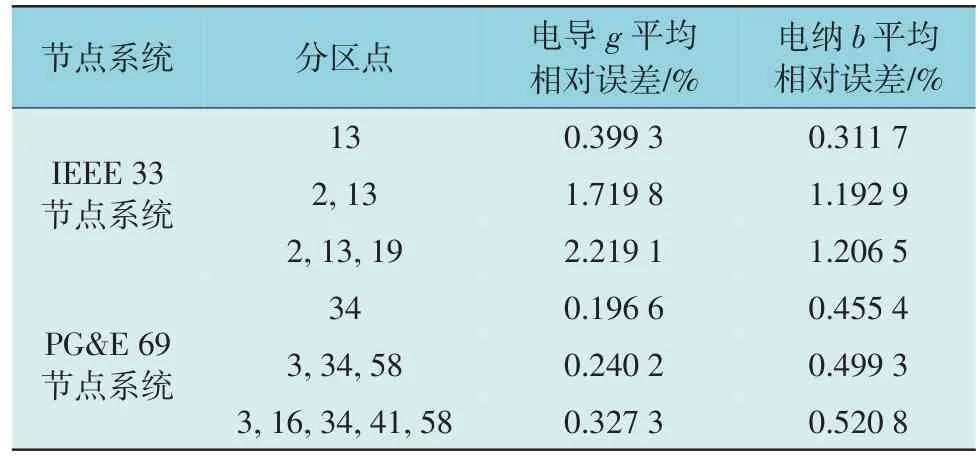
表4 不同分区点下线路参数平均相对误差Table 4 Mean relative errors of line parameters with different partitioning points
4.6 方法对比
本文从初始和精确辨识效果与文献[13]进行了对比,两个节点系统均进行了测试,设定电压误差为0.05%和功率误差为0.5%,文献[13]在精确辨识中使用10 组数据,辨识结果如图8 所示。本文方法大部分线路参数辨识结果是优于文献[13]的,尤其在69 节点系统中表现更佳。
精确辨识结果如图9 所示。由图9 可以看出,本文提出方法显著提升了辨识精度,使参数估计更接近真实值且误差更可观。相比之下,文献[13]方法较依赖所选数据质量,坏数据会导致误差较大。本文采用滑动时间窗和异常值检测策略降低了数据质量问题对辨识结果的负面影响。
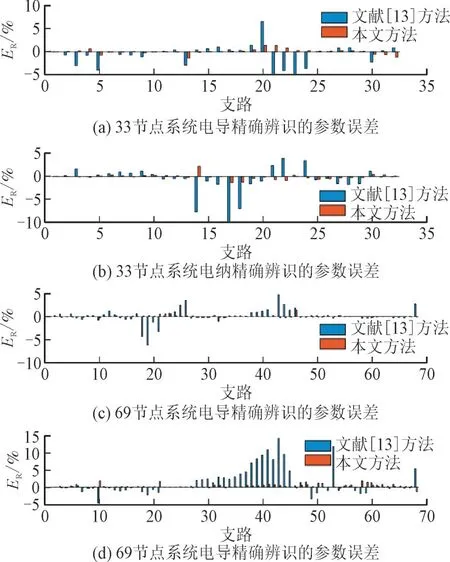
图9 不同方法线路参数精确辨识误差Fig.9 Line parameter precise identification errors for different methods
5 结论
本文提出了一种改进线路参数辨识方法,运用滑动时间窗和网络分区策略,对线路参数辨识方法进行了改进,其结论为:
1)使用LC-PF 模型对初始参数进行辨识,仿真结果表明,其初始辨识结果更加可靠,可以为精确辨识提供更好的初始解。
2)结合滑动时间窗和网络分区策略提高了辨识准确性。
3)仿真测试显示方法在精确辨识后误差小,但存在某些线路参数误差较大需进一步研究,目标是使辨识结果更贴近真实值。
