基于可观性和可计算性的配电网关键量测识别方法
2024-03-24陈培育郑骁麟程茹芸张加东
陈培育,金 尧,郑骁麟,程茹芸,张加东,徐 弢
(1.国网天津电力科学研究院,天津 300384;2.国网天津市电力公司,天津 300010;3.天津大学电气自动化与信息工程学院,天津 300072)
0 引言
与输电网不同,配电网具有拓扑多变[1]、线路参数不准确[2]、三相不平衡、分布式能源[3]大量渗透等复杂特点。由于量测装置的不足和拓扑参数的误差造成配电网的状态估计[4-5](State Estimation,SE)准确率下降[6-8],难以应对可再生能源大量并网带来的系统波动[9],因此迫切需要提高配电系统的可观性[10]和可计算性。
近年来配电网同步相量测量单元(Distribution Phasor Measurement Unit,DPMU)的应用[11-12]在全世界范围内得到广泛关注,其缺点是配置总成本较高。相比较而言,部署馈线终端单元(Feeder Terminal Unit,FTU)采集电压幅值、电流幅值、功率、开关的开断状态等信息[13]在经济上更为可行。在节点数众多、拓扑复杂的低压配电网中,对满足配电网可观性、可计算性、可靠性的量测配置进行综合评估具有重要意义[14]。目前大多数量测配置研究的目标是实现全系统的可观性增强[15-16],有学者通过对不同的状态估计算法进行比较分析,提出用于实现网络可观、提升状态估计精度的最优FTU 配置方法[17],但从经济角度来看通过增设量测设备实现低压配电网的完全可观测是不可行的。拓扑法[18-19]和数值法[20-22]是识别网络中不可观支路的2 种经典方法,部分研究热衷于探索利用数值可观性分析方法增强可观测性维度的关键量测[23],然而在低压配电网中大规模伪量测所包含的大量不确定性[24-25]会在一定程度上影响状态估计结果的准确性。由于信息熵可用来表征量测信息的不确定性[26],因此可通过引入信息熵来表征伪量测不确定性对配电网状态变量的影响。
本文针对量测冗余度较低时传统可观性分析方法对配电网量测部署的指导作用不足的问题,提出基于可观性和可计算性的配电网关键量测识别方法。案例分析表明,所提方法能够在不同网络拓扑结构、差异化伪量测精度和不同状态估计算法下,提供最优的量测配置方案。研究的创新之处在于:(1)拓展了可观性的应用场景;(2)可适配多种状态估计算法;(3)量化了伪量测的引入对于状态感知的影响,为低冗余度配电网增设量测提供了指标参考。
1 可观性分析
1.1 基于线性旋转变换的线性模型
数值法通过分析增益矩阵分解的零主元来确定配电网络是否可观[21],本质上是分析秩与状态变量之间的定量关系,通过记录零主元的位置和支路节点关联矩阵来识别不可观支路。配电系统中线路的阻抗比普遍较高,从而限制了系统有功功率和无功功率的自然解耦,为此引入利用线性旋转矩阵的配电系统可观性解耦数值模型[20],以实现修正有功及无功功率的解耦分析、降低计算复杂度的目的。结合交流潮流方程得到线性旋转变换过程表达式为:
式中:Ui,Uj分别为线路首节点i和末节点j的电压幅值;θij为节点i,j之间的电压相角差;Pij,Qij分别为节点i,j之间的原始有功功率和无功功率;P′ij,Q′ij分别为经过线性旋转变换后节点i,j之间的修正有功功率和修正无功功率;φ为线路阻抗角;X,R,Z分别为线路电抗、电阻、阻抗值;Tij为节点i,j之间线路的线性旋转矩阵。
由式(3)可知,当线路两端相位角差值较小时参照传统直流算法来分析线路有功和无功,可得P′ij与电压相角差线性相关,Q′ij与电压幅值差线性相关,进而可以采用有功与无功解耦模型来简化配电网的可观性分析。
1.2 数值可观性分析
本节以配电网中电压幅值的可观性为例具体说明可观性分析步骤。数值可观性分析方法流程如图1 所示。
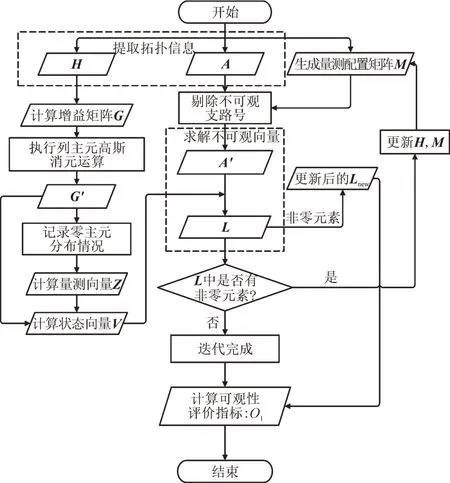
图1 数值可观性分析方法流程Fig.1 Procedure for numerical observability analysis method
图1 中,A为支路节点关联矩阵,A′为剔除不可观支路后的支路节点关联矩阵,H为量测雅可比矩阵,M为量测配置矩阵,G和G′分别为增益矩阵和上三角增益矩阵,V为状态向量,Z为量测向量,L为单次循环得到的不可观支路向量,引入非零元素得到更新后的Lnew。
数值可观性分析的步骤如下:
1)提取拓扑信息。所生成A的行数对应支路数b,列数对应节点数n。生成量测雅可比矩阵H表达式为:
2)生成量测配置矩阵M。确定当前无功功率量测配置情况,若支路包含线路无功测量,对应的元素赋值为1,不含线路功率测量时,则赋值为0。
3)计算增益矩阵G。
式中:GQ-U,HQ-U分别为无功功率对电压幅值的增益矩阵与量测雅可比矩阵。
采用列主元高斯消元法对GQ-U进行处理,得到无功功率对电压幅值的上三角增益矩阵G′Q-U。记录零主元的分布情况并将零元素设置为1,增益矩阵的处理如图2 所示。其中,f为列主元高斯消元运算函数。
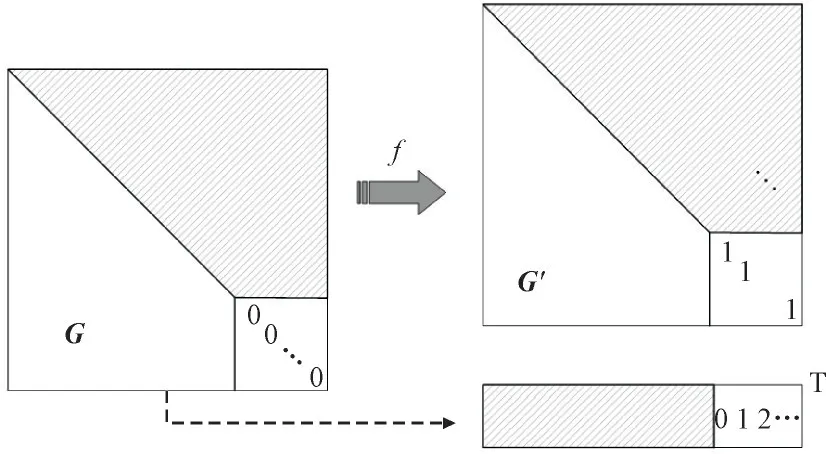
图2 增益矩阵的处理Fig.2 Gain matrix processing
4)计算量测向量Z和状态向量V。通过将G的零主元素对应的位置设置为连续的整数来生成量测向量Z,然后根据公式(6)得到状态向量V,关系表达式为:
5)求解不可观向量。通过式(7)得到不可观支路向量L。
6)计算可观性评价指标O1。移除不可观支路两端的功率注入测量值并更新M和H,重复执行步骤3)到步骤9),直至L中无非零元素时迭代结束。得到不可观支路集合与可观岛划分情况,计算可观性评价指标O1为:
式中:buno为不可观支路数。
2 可计算性评估
从可计算性评估的维度来看,伪量测值通常由历史数据预测生成或非实时量测设备获取。由于系统噪声和通讯问题,导致伪量测中包含较大的误差,但这些因素在传统可观性分析中并未被考虑,同时由于不同机理的状态估计算法在差异化的测量条件和网架结构下表现不同,因此亟需可以适配多种状态估计算法的可计算性评价指标。为此,本文提出利用信息熵来分析状态变量的概率分布、量化网络的可计算性。信息熵可直观的理解为传递信息量的数学期望,随机事件x的信息熵h(x)为:
式中:q为随机事件总数;pr(xδ)为第δ件随机事件xδ发生的概率。
假设对于给定的随机事件存在2 种情况:第1种情况下,A,B,C 3 种结果发生的概率相等,均为33.3%;第2 种情况下,只有A,B 2 种结果且A,B 发生的概率分别为80%和20%。根据式(9)得到2 种情况下PA,PB的信息熵曲面图如图3 所示。其中,第1 种情况的信息熵为1.585 bit,而第2 种情况的信息熵则较小为0.722 bit。这是由于在第2 种情况下随机事件传递的信息量较少,事件结果A 为真实结果的几率较大,所以随机事件的不确定性也相对较小。随机事件的状态分布越集中,信息熵的数值越小,其对状态变量分布的离散程度越敏感。
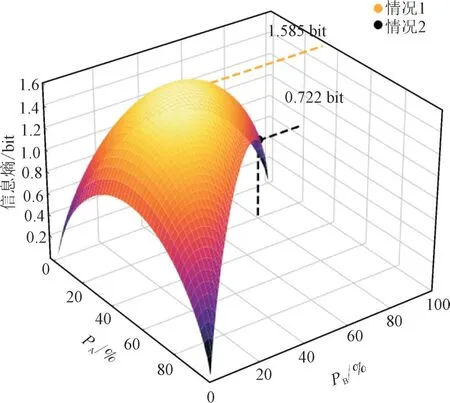
图3 2种情况下PA,PB的信息熵曲面图Fig.3 Surface chart of information entropy for PA,PB in two scenarios
系统信息熵hsys表达式为:
3 配电网关键量测识别
电力系统内的量测可大致分为关键量测和非关键量测。如果一个可观测系统由于移除某个量测而变得不可观,这样的量测被定义为关键量测[27]。但这个概念更适用于输电网中识别网络内测量配置的薄弱点,可针对性的增强状态感知系统的能力。对于量测冗余度很低的配电网来说,为了以合理的经济成本部署额外的量测使网络透明度最大化,还需要进一步缩小关键量测的范围。基于以上考虑,本节提出基于O1和O2的配电网两阶段关键量测识别方法。第一阶段使用数值可观性分析方法计算存量量测下的可观岛划分情况及可观性指标;第二阶段对可观岛边界量测进行测试,计算基于节点信息熵的可计算性指标,最后给出最优量测配置方案。
低冗余度下的配电网关键量测识别步骤如下:
1)应用1.2 节中所提的可观性分析方法,根据当前拓扑信息和量测配置情况,得到当前网络内可观岛划分情况和不可观支路,并计算得到可观性评价指标O1。
2)使用当前存量量测信息对系统进行状态估计并执行蒙特卡洛模拟,计算2.2 节所提基于信息熵的配电系统可计算性评价指标O2。
3)将位于可观岛边界处的量测组成集合,把集合中的元素分别添加到当前网络中,然后依次进行可观性分析(此处只有支路功率量测和支路电流量测被认为是预新增量测)。
4)计算O1的提升情况,筛选出对当前配电网络可观性有贡献的支路集合,集合中的支路数目记为m,制定拟新增量测数目为v,并统计可计算性待测试组合,组合数为。
5)对新增支路量测组合的网络依次进行状态估计,分析蒙特卡洛计算结果并计算O2;筛选出对网络可计算性指标贡献度最高的v个支路功率量测组合(筛选支路功率量测组合数目与步骤4)中拟新增量测数目一致),完成关键量测识别。
4 案例分析
4.1 可计算性分析
以IEEE33 节点配电系统为例,可计算性指标验证的量测部署位置如图4 所示。

图4 可计算性指标验证的量测部署位置Fig.4 Measurement deployment points in verified experiment for computability index
常见状态估计算法包括最小二乘法和电流匹配法。其中,电流匹配法是一种结合潮流分析的状态估计算法,可根据支路功率量测或电流量测的部署情况划分功率修正分区并形成层次关系,通过计算各子区域边界的功率失配量,不断迭代修正负荷功率伪量测,最终收敛到指定的阈值,完成整个系统的伪量测修正和状态量更新[28]。为分别测试不同量测案例、不同状态估计算法对可计算性的影响,设置3 个对比案例的量测配置情况如表1 所示。

表1 3个对比案例的量测配置情况Table 1 Measurement configurations for 3 comparison cases
为测试伪量测对于状态估计精度的影响,设置不同量测参数对应误差如表2 所示。
通过执行蒙特卡洛模拟得到状态变量的概率分布。由于状态变量在数值上是连续的,为简化计算需对状态变量的值进行分箱,每个箱体代表在最小值和最大值之间可能取到的预设值,箱体大小需要根据计算时间和精度进行权衡,本文使用0.005 p.u.。在模拟1 000 次后进行特性分析统计,得到hsys和O2如图5 所示。

图5 可计算性评价指标对比Fig.5 Comparison of computability indicators
由图5 可知,当采用基于最小二乘[29-30]的状态估计算法时,新增4 个子根节点的电压幅值测量后,O2约提升了20%达到82%。由于电流匹配法更适应配电网拓扑和量测部署,同等量测条件下采用电流匹配法时无需提供子根节点电压幅值量测,所以O2在数值上最高可达82.7%。对比结果表明,应用适合实际拓扑结构的状态估计算法可以避免在测量配置上的不必要投资。
4.2 关键量测识别
本文案例采用IEEE33 节点配电系统,初始量测条件下的可观岛与功率修正分区如图6 所示。其中,图6(a)中不同颜色的区域代表不同的可观岛,图6(b)中不同颜色的区域代表不同线路功率量测修正的分区。不同量测参数对应误差参考表2。

图6 初始量测条件下的可观岛与功率修正分区Fig.6 Observable islands and power correction partitions under initial measurement conditions
由图6 可知,图6(a)中存量量测在网络内分布不均匀且不足以支撑配电网完全可观[31-32]。可观性分析表明,量测配置下网络可分解为6 个可观岛,其中含有5 条不可观支路。为方便后续执行状态估计和蒙特卡洛模拟,图6(b)进一步划分功率修正分区,6 个子区域的伪量测分别由各自首端的线路量测修正,由式(7)和式(10)计算可得原始量测条件下O1,O2分别为84.38%,43.23%。通过对可观测岛屿边界上的功率量测进行分析,发现在支路4—5,5—6,6—26,14—15,30—31 上增设量测对O1有提升作用。
对5 条支路分别增设线路功率量测,执行状态估计和蒙特卡洛模拟得到系统电压幅值分箱图和不同新增量测点位下的指标对比如图7—图8 所示。

图7 系统电压幅值分箱图Fig.7 Box plot for system voltage magnitude

图8 不同新增量测点位下的指标对比Fig.8 Comparison of indicators between different new measurement points
由图7—图8 可知,5 条支路都位于可观岛的边界,假设预增设的量测数目为1,所以对指标O1的提升效果相同,均为3.13%。另一方面,通过比较对指标O2的影响,可以发现在支路4—5 上新增线路功率测量所带来的可计算性提升最大,为14.47%,性能明显优于其他位置的量测。因此,在现有的量测条件下,支路4—5 上的线路功率量测可以被确定为关键测量。分析结果表明,支路4—5处于配电系统上游,在此区域安装精度较高的功率量测可以大幅度约束下游节点状态信息的不确定度;支路4—5 上的量测与已安装的线路功率量测具有较远的电气距离,使得不同支路量测获取的量测信息重叠度较小;支路6—26 是一个反例,其虽处于上游区域但与系统原有的支路26—27 量测相邻,使得其部署所带来的修正作用大幅降低仅为1.1%。
5 结语
为应对日益增长的分布式能源渗透和柔性负荷,采用经济可行的方法提高配电系统的状态感知能力至关重要。本文针对量测冗余度较低时传统可观性分析方法对配电网量测部署的指导作用不足的问题,提出基于可观性和可计算性的配电网关键量测识别方法。算例分析表明,即使在配电系统整体不可观的情况下,本文所提方法仍可在综合考虑不同网络拓扑结构、差异化伪量测精度和不同状态估计算法下,提供最优的量测配置方案。
