提高双向调节能力的混合储能平滑风电控制策略

2024-03-24纪坤华邓丽娜

智慧电力 2024年3期

纪坤华，王云，邓丽娜，赵耀

（1.国网上海市电力公司，上海 200120；2.国网江苏常州供电公司，江苏常州 213000；3.上海电力大学，上海 200090）

0 引言

近年来，风力发电在能源供应中的占比越来越高[1]。但是由于风电出力的随机波动性，在大规模并网过程中将会给电力系统带来安全和稳定问题[2]。在风电场出口侧配置储能系统平滑风电出力是一个有效的解决方案[3]。

利用储能平滑风电并网功率的步骤可大致分为获取风电目标出力、功率分配以及能量反馈控制[4]。目前常用的获取风电目标出力的方法有模型预测控制（Model Predictive Control，MPC）[5]、滤波方法[6-7]等。储能的选择与控制方案的设计对功率平滑效果有着重要影响[8-9]，因此储能系统间的功率分配与荷电状态（State of Charge，SOC）的优化控制已成为国内外学者的研究热点。文献[10-12]分别使用了飞轮储能、超导储能、电池储能平滑风电输出功率；文献[13]利用模糊控制根据电池电量、充电状态和俯仰角变化调节一阶滤波器参数；文献[14]使用模糊控制对应用于平滑风电的储能进行了SOC 优化。双储能系统可解决频繁充放电问题，文献[15]基于双电池储能提出了考虑放电深度和频繁的充放电转换对电池寿命的影响的平滑功率控制策略。文献[16]提出了一种考虑是否弃风、预测功率差值以及平抑风电波动3 种目标的多种工况的双储能协调控制策略。但双储能系统因其工作模式的特殊性，充放电能量不平衡问题突出，严重时降低甚至失去双向平滑能力。可以考虑风电波动分量中有不同的频率与振幅的能量型与功率型组成的混合储能（Hybrid Energy Storage System，HESS）往往更有利于平滑风电波动[17-19]。

文献[20-21]研究了自适应变分模态分解获取风电并网功率与HESS 输出功率，但电池需频繁充放电，加快寿命损害。文献[22]提出了分区控制的HESS 控制策略和基于模糊控制的充放电功率修正方法。文献[23]设计了基于模糊下垂系数算法的虚拟RC 下垂控制策略，实现母线电压和SOC 的自恢复。文献[24]中研究了超级电容与氢储能组成的HESS，将SOC 控制在合理区域内，并实现HESS 的最优功率分配。文献[25]研究了基于超级电容与燃料电池的HESS，并将超级电容组划分为2 组分别作为充电堆与放电堆，扩展其放电深度，减小超级电容的充放电次数、延长使用寿命，但电池更易受充放电切换次数影响，且滤波方法平滑风电会加大储能容量配置。因此，单一控制方式的储能充放电切换频繁，加快寿命损耗，单一种类双储能没有考虑风电波动功率中的不同频率分量，且存在能量不平衡问题，而传统混合储能中的电池储能依然需要频繁充放电。

本文提出超级电容与双锂电池组成的HESS 结构，基于MPC 获取风电目标并网功率与HESS 总输出功率；设计以超级电容SOC 为输入的模糊控制调节一阶低通滤波时间常数，实现超级电容与锂电池间的自适应功率分配。设计以锂电池双储能的充放电不平衡度为输入的模糊控制对双储能SOC 进行优化控制，仿真实验分析该控制策略的优越性。

1 风电储能联合系统

本文研究的风电储能联合系统结构如图1 所示，系统由风电场及风功率预测中心、HESS 以及控制器组成。风电场由多个风电机组组成，并将其输出整合为一个总的输出，HESS 包括锂电池和超级电容。与传统HESS 不同的是，本文将锂电池划分为2 组，分别承担充放电任务，组成双储能系统。电池储能的使用寿命主要受充放电切换次数以及充放电深度的影响，由于风电功率波动较大，应用在平滑风电领域的传统HESS 中电池储能仍需频繁充放电。而双储能系统结构中2 组储能分别承担充放电任务的工作模式可确保每组储能较长时间内保持同一状态，当其SOC 达到限值时切换状态，可大大减小电池储能的充放电切换次数。

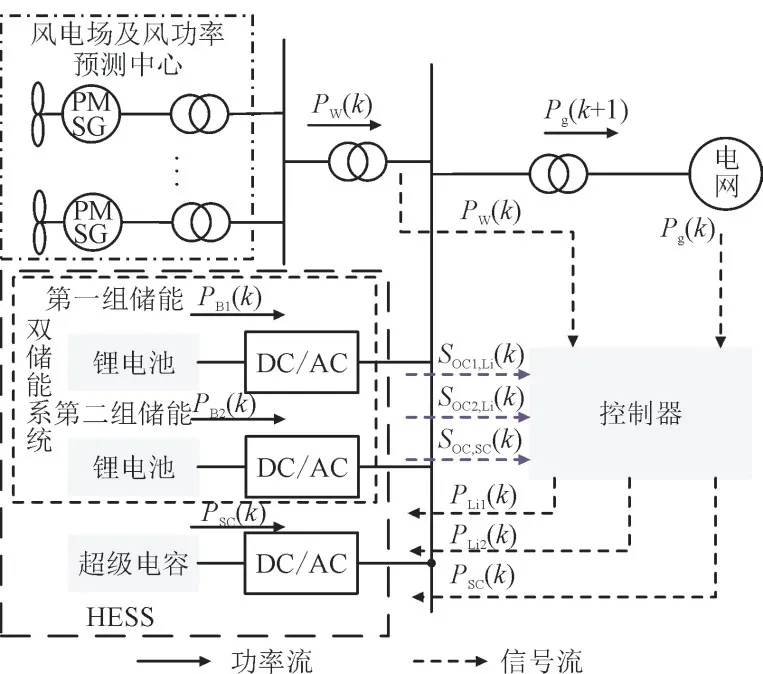
图1 风电储能联合系统结构Fig.1 Structure of wind power-energy storage hybrid system

图1 中PMSG 为永磁直驱风机，PW（k）为k时刻风电实际输出功率，Pg（k）为k时刻的并网功率，PB1（k）和PB2（k）分别为第1 组储能和第2 组储能在k时刻释放功率，PSC（k）为k时刻超级电容的功率，SOC1，Li（k）和SOC2，Li（k）分别为k时刻第1 组和第2 组锂电池储能的荷电状态，SOC2，SC为超级电容的荷电状态，PLi1（k）为在荷电状态为SOC1，Li（k）时控制器控制第1 组储能输出功率，PLi2（k）为在荷电状态为SOC2，Li（k）时控制器控制第2 组储能输出功率。

2 混合储能功率分配

2.1 风电并网目标功率获取

MPC 作为一种闭环优化控制，可有效减少风电波动性与间歇性带来的不利影响[26]。根据系统结构建立预测模型：

式中：x（k），u（k），r（k）与y（k）分别为k时刻状态变量、控制变量、可测扰动变量与输出变量；EH（k）为当前HESS 总剩余容量；PH（k）为k时刻HESS 的总输出功率指令，其值为正表示放电，为负表示充电；A，Bu，Br与C为系数矩阵；Ts为系统采样周期。

假设预测步长与控制步长均为p，输出变量可由状态变量、控制变量与扰动变量迭代得到。

建立目标函数，以HESS 在控制域内出力最小为目标，以减小储能容量配置并延长使用寿命，约束包括并网功率的波动、储能总输出功率及储能剩余容量的约束：

式中：J为控制域内的出力；j为采样数；δ为并网功率允许波动范围；PH，min与PH，max分别为储能的最小、最大输出功率；EH，max为HESS 总最大容量。

2.2 混合储能功率分配原则

由于风电的波动性较大，使用超级电容与锂电池的HESS 系统更有利于储能的健康与长期使用。功率分配时，将持续时间长、变化幅度小的波动分量分配给锂电池，将持续时间短、变化幅度大的波动分量分配给超级电容。总体控制器结构如图2所示。图2 中，Pg为系统总功率与风电并网功率及模糊逻辑2 输出功率三者之和；SOC,SC为超级电容的荷电状态。模糊逻辑控制1 实现超级电容与锂电池间的功率自适应分配，模糊逻辑控制2 实现双锂电池储能间的SOC 优化控制。

图2 功率平滑控制框图Fig.2 Block diagram of power smoothing control

图2 中PHESS为经过MPC 得到的HESS 系统总功率，ΔPb为平滑后得到的低频分量差值，Pwind为风电的目标功率，SOC1和SOC2分别为第一组和第二组储能的荷电状态，PSC为超级电容的总功率，PLi为锂电池的总功率，Tf为一阶低通滤波时间常数。

2.2.1 混合储能初级功率分配

由采用适应性较强、易于实现、灵活性较高的一阶低通滤波方法对信号分解并进行初次功率分配，将低频分量作为锂电池的参考功率，将高频分量作为超级电容的参考功率，如式（5）。

式中：PHESS（t）为经过MPC 得到的t时刻HESS 系统总功率；Pb（t）为平滑后得到的低频分量，即t时刻锂电池总功率；PSC（t）为平滑后得到的高频分量，即t时刻超级电容功率。

Tf越大，锂电池的输出功率越小且越平滑，超级电容输出的功率越大且变化越大。定时间常数的一阶低通滤波在进行功率分配时没有考虑到超级电容的SOC 及其平滑能力。

2.2.2 模糊自适应次级功率分配

超级电容的作用是平抑变化较快的波动功率，将变化相对较慢的功率分配给锂电池以减小电池的充放电切换次数，延长电池储能的使用寿命，并提升储能系统平滑风电输出功率效果。但超级电容因其价格十分昂贵，因此考虑到成本问题，通常情况下，HESS 中超级电容的容量配置较少，也正因如此，其SOC 变化也会更快，相比电池储能，其SOC更容易达到限值。若其SOC 达到限值，则锂电池储能不得不平抑变化较快的功率，其寿命将大大降低，将超级电容的SOC 维持在双向调节能力最强时有利于平滑效果的提升。因此，本文针对超级电容SOC，设计了模糊控制器调节一阶低通滤波时间常数，实现对HESS 的自适应功率分配。

3 锂电池双储能功率分配

HESS 中锂电池的使用寿命受充放电切换次数的影响较大，虽然仅平抑低频分量可一定程度上降低锂电池的充放电切换次数，但由于风电的波动性太大，在平滑时依旧会频繁切换充放电状态，降低使用寿命。因此本文将锂电池储能划分为2 组构成双储能系统，分别承担充电与放电任务。传统双储能中当其中任意1 组储能的SOC 达到设定的限值时工作模式切换，2 组储能的充放电状态同时转换，虽大大减小了储能的充放电状态切换次数，但在每一次状态切换时都会发生SOC 越限，并持续多个采样周期；且存在2 组储能充放电能量不平衡问题，储能将会频繁切换充放电状态，降低甚至失去双向调节能力，无法自我恢复。

3.1 双储能SOC优化控制

双储能策略中，只要一组储能SOC 达到限值，则两组储能同时切换充放电状态，而风电又具有较大的随机性，因此长期运行的储能较易出现充放电能量不平衡，降低双向调节能力甚至失去平滑风电的能力，故本节对锂电池组成的双储能系统进行SOC 优化。锂电池双储能的SOC 不仅受过去出力的影响，也会影响未来的平滑能力，是影响其状态切换的重要指标，当2 组储能的SOC 都很低或都很高时，其双向调节能力也将大大降低。定义双储能系统的SOC 评价指标：

式中：SOC,max和SOC,min分别为最大和最小荷电状态；Ech，Edis为该时刻双储能组充电、放电能力，其值越大，表示充/放电能力越强；S为该时刻系统充放电不平衡指标，其值大于0 时表示充电能力大于放电能力，小于0 时表示放电能力大于充电能力，S的绝对值越大表征充放电能量越不平衡，双向调节能力越低；c1，c2分别为第1、第2 组储能的充电标志，为充电组时其值为1，否则为0；d1，d2分别为第1、第2 组储能的放电标志，为放电组时其值为1，否则为0。

设计模糊逻辑控制，S与Pb为输入，ΔPb为输出，输入量与输出量的论域范围均关于零对称。当不平衡指标S小于0 且较低时，表征双储能系统放电能力大于充电能力，因此适当增大其放电功率。但当该时刻放电功率已经很大时，不予调整，当功率指令为充电时，适当减少其充电功率，由于充电功率为负，因此当模糊逻辑控制的输出ΔPb为正时可减少其吸收的充电功率；同理，当不平衡指标为正且较大时，表征系统充电能力大于放电能力，故当放电时减小其放电功率，充电时增加其充电功率，当ΔPb为负时可增加充电功率。

超级电容的调节功率由锂电池储能承担，调节过后并不影响并网功率，而锂电池SOC 优化不同，双储能调节功率需由并网功率承担，且模糊输出为输出功率增量，因此经过模糊SOC 优化控制后，需考虑并网功率是否还满足波动要求以及电池储能的最终输出功率是否满足其物理限值，并由式（8）与（9）得到最终输出功率指令。

3.2 改进储能工作模式

考虑到传统双储能控制策略的局限，本节对双储能的工作模式进行改进以解决SOC 越限问题。定义PBi，md与PBi，mc为荷电状态为SOCi（k）时第i个储能最大、最小输出功率，前者为正，后者为负，如式（10）。

式中：CLi为每组锂电池的容量；SOCi，min与SOCi，max分别为第i组锂电池SOC 的下限和上限。

经模糊自适应SOC 优化控制后，得到最终双储能输出功率指令，进而计算2 组储能在执行完该指令后是否会存在SOC 越限，从而决定2 组储能的工作模式。若其中1 组储能SOC 越限，则控制2 组储能共同承担该任务。假设第1 组储能在释放PB1（k）的功率后，其SOC 将低于其下限，该限值功率如为式（10）中PBi，md，2 组储能的输出功率调整为式（11）所示。SOC 越上限的情况类似。

式中：PB1，md（k）为第1 组储能在当前SOC 下能输出的最小功率，值为负；PB1，m（k）与PB2，m（k）分别为第1、第2 组调节后的输出功率；PB1，d（k）为当前时刻第一组储能的初级功率，且为充电功率，其值小于零。故而2 组储能共同承担充电任务。

本章所提的锂电池双储能工作模式及其切换示意图如图3。

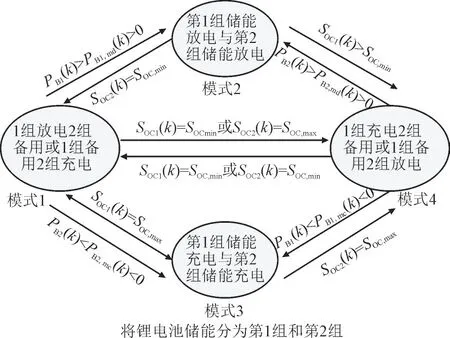
图3 锂电池双储能模式及切换示意图Fig.3 Schematic diagram of dual energy storage mode of lithium batteries and mode switching

4 算例分析

为了验证所提策略的有效性和优势，从国内某100 MW 风电场选取一典型日数据作为实验对象，并在Matlab 平台进行仿真实验。风电场混合储能联合系统拓扑结构如图1 所示，具体参数设计在表1 中给出，控制步长与预测步长均设为15 步，将风电场所有运行的风机输出功率整合为一个总的输出功率，风电场总装机容量为30～150 MW 的风电场，1 min 内的有功功率波动量不得超过总装机容量的10%[27]。表1 中PB,max和PB,min分别为锂电池最大和最小输出功率。根据表1、式（7）—式（8），分别设定双锂电池充电与放电能力相差最悬殊的场景可得充放电不平衡度S的取值范围在[-0.8，0.8]。

表1 参数设置Table 1 Parameter settings

4.1 风电平滑效果分析

本算例对该控制策略的平滑效果进行分析，由于采样间隔为1 min，故1 min 内的功率波动为相邻2 个采样间隔的并网功率差值，如式（12），定义平均波动功率为仿真时间内并网功率波动绝对值的均值，如式（13）：

式中：ΔPg(k)为k时刻相邻2 个采样间隔的并网功率差值；ΔPg,mean为并网功率波动绝对值的均值；N为充放电次数。

获取风电并网目标功率时采用4 种对比方案，分别为方案1：原始风电出力；方案2：本文所提控制策略；方案3：滑动平均法；方案4：一阶低通滤波法。储能的初始SOC 及平滑目标均相同，并网功率如图4 所示，并网波动功率及储能输出情况如表2所示，储能输出情况包括混合储能系统的总最大输出功率及以混合储能总输出的积分值。

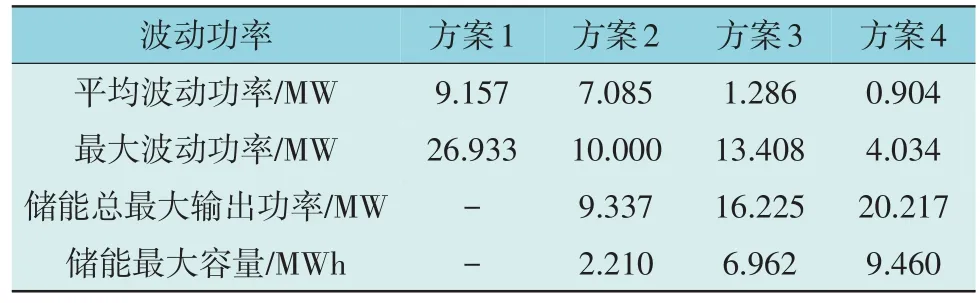
表2 风电并网波动功率及储能输出对比Table 2 Comparison of grid-connected wind power fluctuations and energy storage output among four schemes

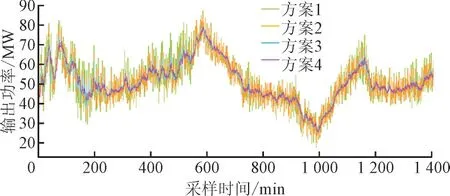
图4 风电并网功率对比Fig.4 Comparison of grid-connected wind power

未经过平滑的风电输出功率波动非常大，相比于未平滑的风电输出功率，在风电场出口侧配置储能系统能有效平抑风电功率波动。方案3 与方案4所获取的并网功率平滑效果最好，但存在过度平滑问题，波动远小于并网要求，但其所需混合储能的功率与容量大小均远高于方案2，因此需要配置更多容量的储能才可达到该平滑效果，且方案3 还存在平滑不充分的问题。而方案2 使用MPC 虽然平均功率波动较大，但由于其良好的预测性能不仅保证了并网功率始终满足并网要求，而且减少了储能的容量与功率配置。

4.2 混合储能容量配置

在本算例中，分析使用本章所提控制策略后HESS 的容量需求，为后续算例中的SOC 计算提供前提条件。首先假设超级电容与锂电池储能的容量足够大，对输出功率进行积分可得到超级电容与锂电池的能量变化情况，如图5 所示。

图5 混合储能系统容量变化曲线Fig.5 Curves for change in capacity of HESS

SOC 为剩余容量占额定容量的百分比，与初始荷电状态SOC0、输出功率及额定容量Erate有关，参见式（14）。为安全起见，SOC 需约束在限值范围内，从而得到考虑安全裕度γ（取1.05）的最小容量如式（15）。据此计算超级电容与锂电池的最小容量，图7 已给出超级电容与锂电池的容量变化曲线，因此得到超级电容的最小容量为0.21 MWh，锂电池双储能每组配置相同容量，按容量需求较大的一组锂电池的容量配置，故锂电池每组储能的最小容量为1 MWh。

式中：P(t)为t时刻功率；E(t)为t时刻容量。

4.3 混合储能模糊自适应功率分配

经MPC 得到HESS 输出功率后对功率进行模糊自适应时间常数的一阶低通滤波获得次级分配，将高频分量分配给超级电容，其余低频分量分配给锂电池储能，最终功率初级分配结果如图6 所示。对比2 类储能的功率分配情况，可以看出锂电池的总输出功率曲线明显稀疏于超级电容的输出功率曲线，超级电容的加入可以进一步减少锂电池储能的充放电切换次数，延长储能寿命。

图6 混合储能系统输出功率Fig.6 Output power of HESS

4.4 双锂电池SOC优化功率分配

为证明本文所提基于模糊控制的锂电池双储能SOC 优化的有效性，当2 组锂电池的初始SOC均为50%时双向调节能力最强，此时无法明确体现该控制的优势。为此设置2 组储能的初始SOC 接近且均处于很低的状态，即初始SOC 为15%，此时不平衡指标为0.7，即充电能力远大于放电能力，按最小容量配置，对比有无SOC 优化控制的2 组储能SOC 变化，如图7。

图7 双储能SOC变化Fig.7 Changes in SOC of dual energy storage system

无SOC 优化控制的双储能将在该情况下总切换76 次，且2 组锂电池的SOC 多在[0.1，0.2]区间变化，两组锂电池的SOC 很接近，其不平衡度也始终在0.7 附近，无法改善充放电不平衡问题，且该状态将始终持续，而采用本章设计的模糊SOC 优化控制后，双储能总切换次数仅为12 次，SOC 迅速调节至理想范围，且2 组SOC 范围在[0.1，0.9]，不平衡度由0.7 迅速恢复至0 附近，双向调节能力迅速提高至最大，由此，证明了本文设计的模糊SOC 优化控制的明显优势。

为证明本文所设计的模式切换及其相应切换原则的有效性，由图7 中SOC 变化曲线可知，无论其进行多少次充放电状态切换，都有效避免了SOC越限，2 组储能的SOC 均处于规定范围内。

为证明本文所提HESS 系统结构可大大减小电池储能充放电切换次数，在储能初始SOC、平滑目标、储能的功率与容量约束均相同时，设置对比方案5：单一类锂电池储能系统；方案6：超级电容与单一控制锂电池的HESS；方案7：超级电容与锂电池双储能系统但无SOC 优化控制，分别与本文所提策略即方案2 对比，其结果由表3、表4 给出。

表3 各方案中锂电池充放电切换次数Table 3 Charging/discharging switching times of lithium batteries with different schemes

表4 平滑能力对比Table 4 Comparison of smoothing capability

同时给出一个表征平滑能力的指标Sav，即充放电不平衡能力的平均值，如式（16）所示，平滑期间Sav愈接近0，该系统的平滑能力愈强，Sav愈接近0.8或-0.8，该系统的平滑能力愈弱。

式中：k1为充放电的次数。

由表3 和表4 可知：（1）相比于单一储能系统，混合储能系统中的超级电容可以一定程度上减少锂电池的充放电切换次数；（2）锂电池储能系统中，双储能控制方式可以大大减小其充放电切换次数；（3）考虑2 组锂电池的SOC 进行优化的控制方式（方案2）可以在极端条件（充放电不平衡）下提高其充放电能力，从而减小充放电切换次数；（4）方案2的平滑指标优于同为双储能控制方式的方案7，初期存在充放电不平衡时，方案2 的平滑能力要强于方案7，在初期充放电平衡时，方案2 与方案7 的平滑能力相当。由此证得，本文所提基于超级电容与锂电池双储能的HESS 在充放电平衡与极不平衡时都可以迅速调节锂电池双储能的SOC，减小其充放电切换次数。