灰犀牛事件对A股不同板块的冲击效应
——基于DCC-GARCH-VaR 模型的实证研究
2024-03-24靳博同
靳博同
(河南财经政法大学金融学院 河南郑州 450016)
1 引言
1.1 研究背景与研究方法
研究中国股市不同板块与中国香港股市的联动性和冲击效应,不仅有助于为跨市场投资者有效进行国际资产的行业组合配置、防范金融风险等提供重要参考,还有助于丰富金融市场相关性的理论成果,更有助于为国家监管金融行业和股市提供政策依据,为从个人到国家的金融风险控制提供借鉴意义。
本文采用多变量DCC-GARCH模型研究中国沪市与港市的联动关系。其中,将香港地区作为 “世界冲击因素 ”,分别考察上证指数各行业板块指数与恒生指数的联动性。分别比较不同行业板块指数与恒生指数条件相关系数的动态变化,分析中国股市各板块面对世界市场的冲击效应,并探讨导致这一结果的原因。
1.2 已有文献回顾
1.2.1 ARCH--DCC-GARCH模型的理论研究
ARCH(Autoregressive Conditional Heteroscedasticity)模型首次由Engle(1982)提出,用于测算平稳时间序列数据的特征;随后ARCH模型不断得到拓展: 而Engle (2002) 提出的 DCC (Dynamic Conditional Correlation)-MGARCH 模型就是本文所要使用的实证模型的基础。该模型可以输出多个变量之间的条件动态方差和条件动态相关系数,有效简化了随时间波动的条件方差及协方差矩阵的计算复杂度。
1.2.2 DCC-GARCH(GARCH-VaR)模型的实证研究
目前,现有文献进行的DCC-GARCH模型实证研究主要集中在两点:一是衡量金融传染与冲击效应,度量不同金融市场/不同行业之间的动态联动机制(杨子晖等,2019;Chittedi, K. R,2015;谷耀和陆丽娜,2006;贾凯威,2014);二是分析多种资产大类之间的动态连接性和不同资产的收益动态相关性,为资产配置与投资提供借鉴和指导(Wenting Zhang等,2022;Joyo AS和Lefen L,2019;郑振龙和杨伟,2012)
其中,在衡量金融传染与冲击效应方面,以全球不同国家的股市、外汇市场为研究对象的文章较多,但对股指中不同板块进行分析较为缺少,本文就行业板块层面进行实证研究与分析。
1.3 研究意义
本文可能的边际贡献:通过DCC-GARCH-VaR模型将研究对象深入行业板块层面,并在数据选择方面采用小样本区间,放大分析个别灰犀牛事件的冲击效应,为DCCGARCH-VaR模型在行业板块层面的研究提供参考。
1.4 文章架构
本文首先给出模型设计和数据说明;其次,根据研究目的进行实证分析;最后,得出实证结论与建议。
2 模型设定和数据说明
2.1 DCC-GARCH模型
DCC-GARCH模型的参数估计分为三步:首先,构建每个股票指数的对数收益率所构建的单变量GARCH模型;其次,用单变量GARCH模型得到的条件方差计算出标准化残差;最后,估计出动态条件相关系数。
Engle(2002)所定义的动态条件相关系数结构如下:
假设组合中各资产的权重为w,收益率为r,则t+1时刻的组合收益率为:
从而组合的波动率可以表示为:
因此,对于组合波动率的估计可以转化为估计资产组合协方差阵的估计,协方差阵的对角线即单个资产的波动率,较容易进行估计,非对角线元素只需估计资产间的相关系数。
对相关系数的估计总体有两类模型:一类是常相关系数模型,即资产间的相关系数不随时间变化,可用一个常数来衡量,如可以用历史数据的相关系数作为估计量;另一类是时变相关系数模型,认为相关系数是随时间变化的,可通过DCC模型进行建模。DCC对相关系数进行建模的方法有以下两种:
方法一:与RM方法原理类似,通过指数平滑的方法对相关系数建模,后文统称为DCC-RM模型,公式(公式中的“ε”即标准化收益)如下:
方法二:即 DCC-Garch模型,公式如下:
式(5)中:ρi,j,t为每两个资产之间的相关系数,即ρ的标准化,通过对ρ标准化从而保证相关系数绝对值小于等于1。
这两种方法最大的区别是,RM方法不满足均值回归现象(右边两个系数和为1),Garch方法在(α+β<1)的情况下满足均值回归现象,与实际相符。
矩阵形式可以表达为:
模型参数估计:
正态性假设下,上述两个模型均可通过极大似然估计法估计参数,在仅有两个资产的情况下,对数似然函数可以表示为:
基于上式,讨论DCC-Garch模型的参数估计过程。DCC-Garch
两资产情况下:
2.2 VaR模型
VaR的计算方式有多种,主要可分为三种:方差-协方差法、历史模拟法、蒙特卡罗模拟法,本文采用方差-协方差方法进行VaR值的计算。
假设所有的单个资产收益率都服从正态分布,资产组合的收益率是单个资产收益率的加权和,也服从正态分布,这种情况下,计算VaR只需对组合的波动率给出估计。如果单个资产收益率不服从正态分布,比如t分布、渐进t分布等,组合的分布就不容易刻画。因此,本文的实证都假设单个资产收益率均服从正态分布,对其他分布的建模需要用到copula等函数,不在本文的讨论之内。因此,资产组合的VaR定义为:
式(12)中:波动率和分布函数为组合的波动率和分布函数。
2.3 数据说明
本文选用香港恒生指数、上证综合指数有色金属、钢铁、煤炭、消费饮食、医药生物、国防军工等板块指数(基于申银万国一级行业分类标准)的每日对数收益率作为样本数据,收益率计算方式为:(其中,pt为某项资产在t时刻的价格)。样本区间为2022年2月24—2022年4月26日。同时,考虑到香港证券交易所和上海交易所交易日的差异,剔除上证综合各板块指数4月15日、4月18日和香港恒生指数4月4日的数据。本文数据均来自choice数据库。
3 实证分析与结果
3.1 DCC-GARCH模型假设检验
基于GARCH模型的假设,在进行模型的参数估计前,本文需要对样本数据进行正态性检验、异方差性检验、平稳性检验和ARCH效应检验。
3.1.1 异方差检验
对每个板块的收益率序列图进行观察,分析异方差现象。
由各板块的收益率序列图观察得出,收益率序列均表现出尖峰和聚类性特征,较大的波动发生在更长时期,较低的收益往往跟随着小波动值,在一定程度上表明了各个板块指数的收益率序列的波动性具有条件异方差现象。
3.1.2 Shapiro-Wilk检验
用来检验序列是否服从正态分布,由于本文采用的数据量小于5000,故采用适用于小样本正态检验的Shapiro-Wilk检验(以有色金属板块为例)。
表1的检验结果为P值>0.05,说明接受原假设,数据呈正态分布;经过检验,各个板块除了石油和军工板块数据不符合正态分布外,其余板块均符合正态分布。

表1 样本描述性统计量和Shapiro-Wilk检验结果
3.1.3 ADF检验(单位根检验)和PP检验
用来检验时间序列是否平稳(平稳为建立ARCH模型的前提,若不平稳,可能引起伪回归问题)Granger等(1974)。
结果显示:序列的ADF检验统计量和PP检验统计量都小于1%的临界值,表明至少可以在99%的置信水平上拒绝原假设。各市场股票收益率序列均通过了单位根检验,序列平稳,适合进行DCC-GARCH回归分析,避免了伪回归。
3.1.4 ARCH-LM检验(拉格朗日乘子检验)
使用ARCH-LM(拉格朗日乘子检验)结果模型分析是否存在ARCH效应。
检验结果显示,ARCH统计量表明收益率序列在1%的显著性水平上拒绝原假设,即存在显著的ARCH效应,同样说明数据存在异方差现象,与图1中所得判断完全一致。
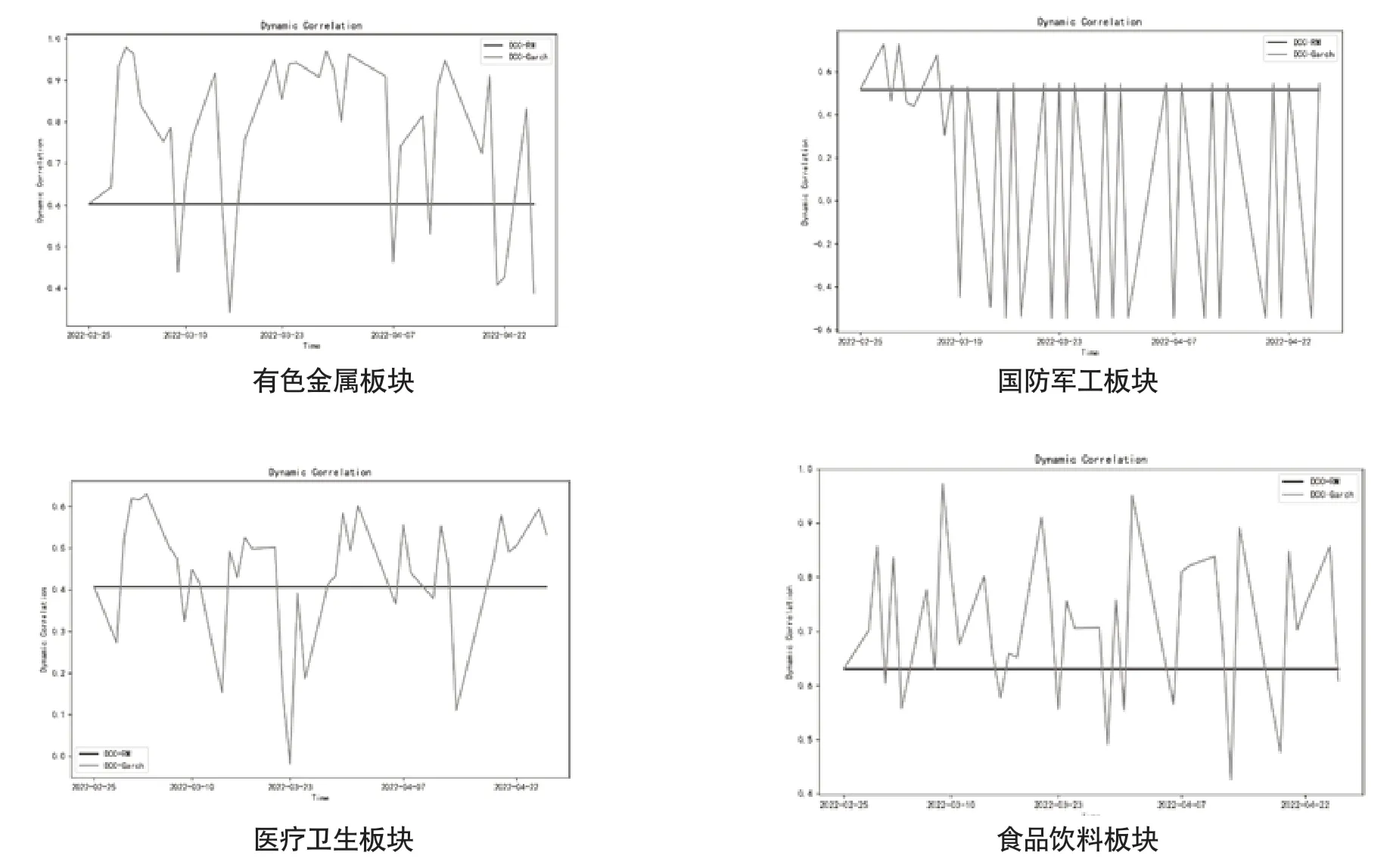
图1 各板块指数与恒生指数条件动态相关系数
3.2 DCC-GARCH模型的参数估计
表2中模型参数的估计结果显示,α、β均显著不为零,说明滞后一期的标准化残差对条件动态相关系数影响显著。β不仅显著不为零还非常接近于1,反映出相关性具有非常强的持续性特征。此外,α、β具有明显的统计显著性,由此判断各板块与恒生指数之间一定存在动态可变的条件相关系数。

表2 DCC模型参数估计表
众多实证研究结果表明,GARCH(1,1)模型可以很好地刻画金融资产收益率的特征,因此对于单变量 GARCH 模型和条件相关结构的估计中,本文采用最简洁的GARCH(1,1)和DCC(1,1)模型,利用DCC模型估计出的参数来计算上证综合指数各板块与恒生指数的动态条件相关系数如图1所示。
从图1可以看出,通过各个板块指数与恒生指数的每日对数收益率所估计出的条件动态相关性存在很大的波动性。除了国防军工板块,主要集中在0.4~0.7的范围之间,最高时的相关性接近0.95,而两者最低的相关性则低于-0.6。
资源类板块如有色金属、煤炭、钢铁板块与恒生指数的相关系数波动较大,且多为正相关,国防军工板块与恒生指数总体呈负相关关系,在恒生指数下跌时能逆势上涨,正与战争的背景相符;而医药生物板块和食品饮料板块与恒生指数的相关系数相对较缓则与板块本身的逆周期属性有关。
由图2可以看出,方差是随时间改变的,很好地验证了关于股市波动时变性的假设。从图2还可以观察到,中国香港恒生指数的波动在三月明显有一个峰值,而与峰值波动较相似的就是有色金属、钢铁、煤炭等资源类板块,军工、医药生物和食品饮料等防守型行业波动则总体较为平稳。总体来看,香港恒生指数作为反映国际金融传染效应的窗口,波动率较大,而上证指数各板块波动有所差别,基本与当时国内国际经济社会背景和板块属性相一致。

图2 板块指数与恒生指数条件方差序列
图3为置信度为1%的组合VaR值分布,总体VaR值分布集中于3%~6%。其中,在4%~6%的VaR值区间内,有色金属板块28天,钢铁板块12天,煤炭板块27天,国防军工板块16天,医药生物板块21天,食品饮料板块27天;大于6%的VaR值区间内,有色金属板块10天,钢铁板块7天,煤炭板块12天,国防军工板块4天,医药生物板块4天,食品饮料板块7天。通过板块表现比较得出,医药生物板块、食品饮料板块的总体平均VaR值较小,国防军工板块受战争背景影响,总体平均VaR值也相对较小;而有色金属、煤炭等资源行业板块的总体平均VaR值相对较大,这一情况与行业属性和上证综合指数的结构特点息息相关,展现出量化的在险价值作为风险衡量的优良指标之一,对不同行业板块的投资决策具有一定的借鉴意义。

图3 基于DCC-GARCH计算的组合VaR值频数分布
4 结论与建议
在战争、全球公共卫生事件、美元加息的世界背景下,上证综合指数作为日益开放的股票市场的波动性较为剧烈,受到的冲击效应较为明显,其各行业板块的波动率和相关系数受股市资本结构、政策等因素的影响部分出现与行业属性有所背离。与香港恒生指数相比,面对金融效应传染和风险冲击的波动相对较小,可能与香港地区作为开放程度较高的国际金融中心有一定关系。本文使用DCC-GARCHVaR模型刻画相关系数随时间的波动趋势并估计条件方差,由此计算出VaR值,对投资者进行行业选择与组合有一定的指导意义,具体如下:
(1)投资者应注重行业选择和配置,分散降低风险。
(2)虽然历史不一定会重演,但总是惊人的相似。投资者应参考和利用历史数据,并从实证角度分析,结合投资组合理论,在投资股票市场时审慎选择行业,注意考察行业的波动性及之间的相关性,避免在相关性较强的行业板进行投资。
(3)多元配置资产大类:如ETF、债券和股指期货等,投资者可以考虑债券+股票+股票指数期货等系统性风险度量指标优良的投资组合。
(4)实证结果分析表明,在俄乌冲突等灰犀牛事件发生的背景下,中国股票市场(以沪市为代表)在能源资源类行业板块的波动较大,在食品饮料行业、医药生物、国防军工行业板块的波动较小,投资者可以选择波动性较小的行业进行波段投资,以降低风险。总体来看,香港恒生指数作为反映国际金融传染效应的窗口,在波动率上的溢出效应较为显著,投资者在选择港股进行投资时应注意把控风险。
