基于Bayes-LSTM 的公路隧道围岩变形预测方法研究

刘智，李欣雨，李震，孔宪光，常建涛

（1.中交第一公路勘察设计研究院有限公司，陕西 西安 710076；2.西安电子科技大学，陕西 西安 710065）

0 引言

在公路隧道施工过程中，围岩大变形是一种常见的施工灾害，对隧道的正常施工具有较大的影响［1］，隧道的监控量测工作对隧道的安全施工具有指导作用。由于隧道围岩的地质条件差异，使其具有较大的各向异性、非均质性、非连续性，导致隧道变形的理论计算较为困难。因此，在建设过程中利用稳定性或收敛变形预测方法辅助判断围岩的变形趋势及稳定性［2］，将对支护设计提供重要参考，避免施工中安全事故的出现。

目前，国内外众多学者对公路隧道围岩变形预测展开了大量的研究。张云鹏等［3］为解决围岩大变形中出现的高度非线性时序问题，采用高斯过程回归构建隧道围岩大变形预测模型；孙柏林等［4］提出含有4 个参数的增长曲线Richards 模型，可以较好地应用于隧道开挖施工过程中的围岩变形预测；曹孟潇等［5］将神经网络预测模型与马尔科夫链结合应用于公路隧道围岩的开挖变形预测；冯永年［6］通过分析隧道围岩的收敛变形特征，基于宴家隧道典型断面开挖过程中的实测围岩收敛变形数据，建立了宴家隧道围岩收敛变形预测GM（1，1）灰色模型；廖烟开等［7］采用挤压因子法对某软岩隧道挤压性大变形等级进行预测，然后采用隧道周边应变法对挤压性大变形的量值进行预测；文明等［8］提出非线性自回归时间序列预测模型，引入动态施工影响因子作为附加的外部输入，提高了模型的预测精度和适应性；周冠南等［9］通过构建基于遗传算法的BP 神经网络智能反分析系统（GA-BP），实现了遗传算法自动搜索BP 网络参数，大大提高了反演分析的效率；刘艳明［10］针对石牛岭隧道出口右洞地表预固结处的灌木丛中发生地表塌陷问题，结合观测现象与量测数据对造成塌陷的原因进行分析，并采用曲线拟合的方法对隧道围岩未来的发展趋势进行预测；李贤等［11］通过对围岩蠕变特性的理论-位移公式计算和现场监控量测数据的回归分析，得出了中和村隧道围岩变形规律和二次衬砌最佳支护时机的参考范围。

Shi 等［12］运用了支持向量机（SVM）信息粒化方法预测围岩的变形，具有较高的精度；曹怀宇［13］在收集现有隧道围岩分类数据的基础上，运用粗糙集理论探索数据中包含的隐性知识，以实现隧道围岩的分类预测；王开洋等［14］通过物理、化学试验确定其壁岩软岩为非膨胀岩，并预测了这些软岩的挤压变形，结合原位应力的实测数据和数值模拟结果，说明了隧道区域最大主应力的分布；Pan［15］结合萤火虫算法（FA）和非线性自回归（NAR）动态神经网络方法，提出了一种用于预测动态非线性围岩变形的算法模型；黄永红［16］运用了MGM（1，3）+AR（3）模型组合，不仅可以反映序列数据发展和变化的趋势，而且可以考虑数据序列中随机波动的影响，可以拟合并进行高精度的预测。

针对围岩变形的动态预测，循环神经网络（Recurrent Neural Network，RNN）的内部节点采用递归连接的方式，使各个隐藏层之间能够相互连接，更好地实现网络状态反馈。长短时记忆网络（Long Short-Term Memory，LSTM）是循环神经网络的变体，可以解决RNN 无法处理长距离的依赖问题，能够更好地处理时序数据。

基于以上研究，本文采用LSTM 模型对拱顶沉降与周边收敛进行预测。首先针对拱顶沉降与周边收敛构建初始LSTM 模型，贝叶斯（Bayes）模型优化初始模型中的超参数，然后利用优化后的LSTM 模型预测拱顶沉降与周边收敛，最后与神经网络（Convolutional Neural Network， CNN）和支持向量回归（Support Vector Regression， SVR）模型分别进行对比，以均方根误差ERMSE评价各模型的预测精度。核心技术方法与杨背背等［17］针对滑坡位移动态预测方法相似。

1 Bayes-LSTM 模型构建

1.1 LSTM 网络基本原理

LSTM 网络是一种改进的循环神经网络，能够规避RNN 中梯度爆炸和梯度消失的问题。所有RNN 都具有一种重复神经网络模块的链式形式。在标准的RNN 中，这个重复的模块只有一个非常简单的结构，RNN 网络结构如图1 所示。

图1 RNN 网络结构Figure 1 RNN structure

图1 中：ht为t时 刻 隐 藏 层 的 状 态 值；xt为 当 前 时刻输入层的输入向量。

RNN 单元的计算公式为：

由式（1）可以看到：RNN 本时刻的隐藏层信息只来源于当前输入于上一时刻的隐藏层信息，没有记忆功能。

LSTM 也具有这种链式结构，如图2 所示。显然，LSTM 的网络结构相比于RNN 复杂了很多，从微观上看，LSTM 引入了细胞状态。同时，LSTM 拥有3 个“门”，分别为“遗忘门”“输入门”“输出门”，其能够靠一些“门”的结构让信息有选择地影响循环神经网络的每个时刻的状态，有选择性地决定让哪些信息通过。

图2 LSTM 网络结构Figure 2 LSTM network structure

LSTM 的第一步“遗忘门”决定细胞状态需要丢弃哪些信息，其决定了上一时刻的单元状态Ct-1对当前时刻单元状态Ct的影响程度，ft为遗忘门的输出，上一序列中隐藏状态ht-1与当前时刻的序列数据xt作为输入，σ为激活函数（常用Sigmoid 函数），bf为遗忘门的偏置向量，Wf为遗忘门权值矩阵。

第二步“输入门”决定给细胞状态添加哪些新的信息，由两部分组成，计算公式如下：

式中：it决定更新到细胞状态中的所需信息；Ct为t时刻新的单元状态；Wc为输入门权值矩阵；bc为输入门的偏置向量；激活函数tanh 为双曲正切函数。

首先，利用ht-1和xt通过输入门的操作决定更新哪些信息，然后利用ht-1和xt通过tanh 层得到新的候选细胞信息，随后更新旧细胞信息Ct-1为新细胞信息Ct。

第三步“输出门”根据输入的和来判断输出细胞的哪些状态特征，控制Ct对ht的影响程度，其更新公式如下：

式中：ot决定细胞状态的输出部分；bo为输出门偏置向 量；Wo为 输 出 门 权 值 矩 阵；ht为t时 刻xt对 应 单 元的隐藏层状态值。

1.2 贝叶斯优化原理

贝叶斯优化是一种近似逼近的方法，用高斯过程、随机森林等各种概率代理模型拟合超参数与模型评价之间的关系，得出效果最好的超参数组合。其适用于黑箱优化（即无需知道函数具体表达式，只需指定输入和输出即可），贝叶斯参数优化会考虑之前的参数信息，更新目标函数的后验分布，直到后验分布基本贴合于真实分布。

贝叶斯优化中的概率代理模型指通过某种概率模型替代目标函数，则后验概率的更新公式为：

式中：D={(x1，f1)，(x2，f2)，…，(xn，fn)}为已采集到的样本点；p(f)为先验分布，能够通过上述贝叶斯公式算出f的后验分布。

贝叶斯优化的代理模型主要分为以下3 类：TPE（Tree Parzen Estimator，树形Parzen 评估器），SMAC（随机森林回归），GP（高斯过程）。本文采用TPE，一种基于树状结构 Parzen 密度估计的非标准贝叶斯优化算法，相比于其他模型，其在高维空间表现的效果更好，速度有显著提高。

TPE 参数配置空间是树形的，主要对p(x|y) 和p(y) 进行建模［9］，前面的参数决定了后续要选择使用哪些参数以及参数的取值范围。

TPE 定义了如下两个概率密度：

式中：l(x)为f(xi)小于阈值y*对应的{ }xi的概率密度；g(x)为f(xi)大于阈值y*对应的{xi} 的概率密度。

通过不同的位置反复测量待优函数，可以获得更多的信息来估计待优函数的分布，从而搜索到最优的测量位置，以期得到最优函数值。为了评估位置是否最优，需要采集函数，在最佳位置采集函数拥有最大值，在TPE 中其采集函数为增益期望（Expected Improvement，EEI），即f(x)小于阈值y*的期望，其在多数情况下表现较好，公式如下：

式中：模型p是观测域上的后验高斯分布。

TPE 中 ，令γ=p(y＜y*)，并 且p(x)=，则有：

式中：l(x)求出概率较高的x，g(x)求出概率较小的x，EEI较大，l(x)和g(x)用树结构形式表示，会更加便于根据l(x)采样，得到更多的改进信息，在每一轮迭代中都会返回有最大EEI的x*。

贝叶斯优化问题包括目标函数、域空间、优化算法、结果历史记录4 个部分，如表1 所示。

表1 贝叶斯优化的主要部分Table 1 Main components of Bayesian optimization

2 基 于Bayes-LSTM 的 模 型 构 建

考虑公路隧道围岩变形的时序特征，利用python构建包含输入层、隐藏层、输出层等部分的LSTM 网络模型，如图3 所示。Python 中的Keras 是基于TensorFlow 的深度学习框架，更是一个高度模块化的神经网络库。基于Keras 框架构建三层神经网络结构。在构建过程中，利用python 中贝叶斯优化调参模块Hyperopt对LSTM 单元内隐藏层尺寸大小（units）、优 化 器（optimizer）的 选 择、学 习 率（learn_rate）、Dropout比例、迭代次数（epochs）等参数针对不同数据集进行优化，选用均方误差EMSE作为损失函数，不断训练调节超参数，直到参数满足精度要求，公式如下：

图3 Bayes-LSTM 模型Figure 3 Bayes-LSTM model

式中：yi为真实值；y^i为预测值。

试验时利用python 语言进行模型搭建与数据处理，具体步骤为：

（1） 分别针对拱顶沉降与周边收敛的机理知识进行分析。

（2） 加载数据，对数据进行归一化处理，将时序数据转化为有监督数据，并将数据转化为LSTM 所需的输入数据格式。

（3） 划分数据为训练集、验证集与测试集。

（4） 设置贝叶斯优化的参数及搜索空间，构建LSTM 网络模型。

（5） 加载LSTM 模型，并对待优化参数进行贝叶斯优化，以EMSE作为损失函数，根据训练集验证集损失判断模型拟合效果，效果好则进行预测，效果一般则调整参数寻优范围继续优化。

（6） 通过反归一化获得预测数据。

3 模型实现与验证

为了验证模型的准确性与有效性，选取某高速公路隧道拱顶下沉与周边收敛数据进行分析，该隧道围岩等级主要为Ⅲ、Ⅳ、Ⅴ级，Ⅴ级围岩测量间距为10 m 左右，Ⅳ级围岩测量间距为20 m 左右，Ⅲ级围岩测量间距为50 m 左右，在隧道开挖毛洞的拱顶及轴线左右各2.5 m 共设3 个带挂钩的锚桩（或粘贴反光片），测桩深度30 cm，用快凝水泥或早强锚固剂固定，利用全站仪进行测量。

3.1 基于Bayes-LSTM 的拱顶沉降预测模型与验证

选取该隧道左线ZK58+820 横断面的3 个测点C1、C2、C3 的拱顶变形监测数据进行分析，该断面的围岩等级为Ⅴ级，测点布置如图4 所示。

图4 拱顶下沉测点布置示意图Figure 4 Layout of measurement points for crown settlement

持续观测59 d 的拱顶沉降监测数据（包含C1、C2、C3 测点）如图5 所示。前47 d 的监测频率为1次/d，由于拱顶下沉逐渐趋于稳定，因此后12 d 的监测频率为1 次/（3 d）。

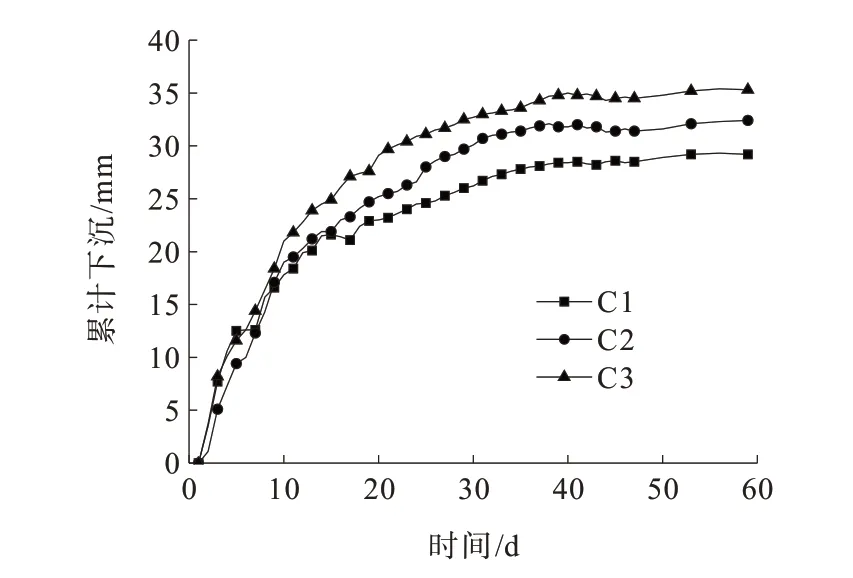
图5 拱顶沉降曲线Figure 5 Crown settlement curve

为了提高模型的泛化能力，防止过拟合现象，将前67%的数据作为训练集，用于贝叶斯优化寻找最优模型参数，后33%的数据作为测试样本进行预测。设置贝叶斯优化过程中迭代次数为30，以训练集中的20%作为验证集来验证模型的泛化能力，优化目标为均方误差EMSE，所选取的需要进行优化模型参数及其参数空间与得到的各个最优参数如表2 所示。重新使用全部训练集对模型进行训练，最终得到最优模型。

表2 贝叶斯优化的参数空间及其最优参数Table 2 Parameter space of Bayesian optimization and its optimal parameters

针对拱顶下沉C1 的实测数据，首先对数据进行归一化，由于监测天数非连续，本文利用前两天的累计沉降数据与监测天数作为特征因素来预测第三天数据，并将数据转化为有监督数据，如表3、4 所示。

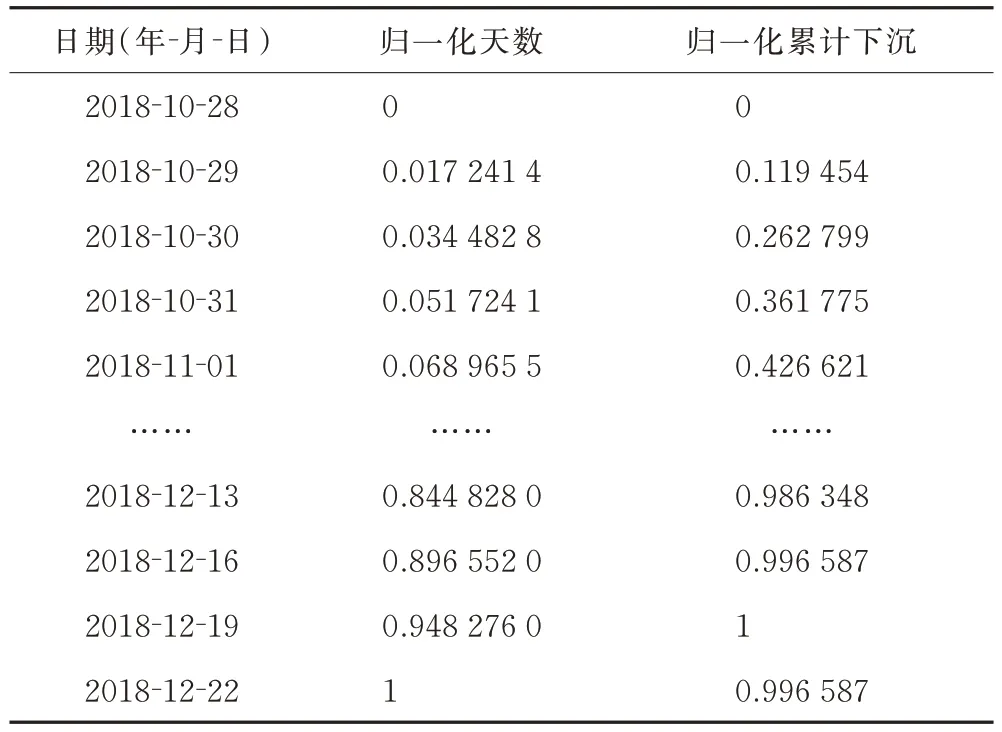
表3 C1 测点归一化后数据Table 3 Normalized data of C1

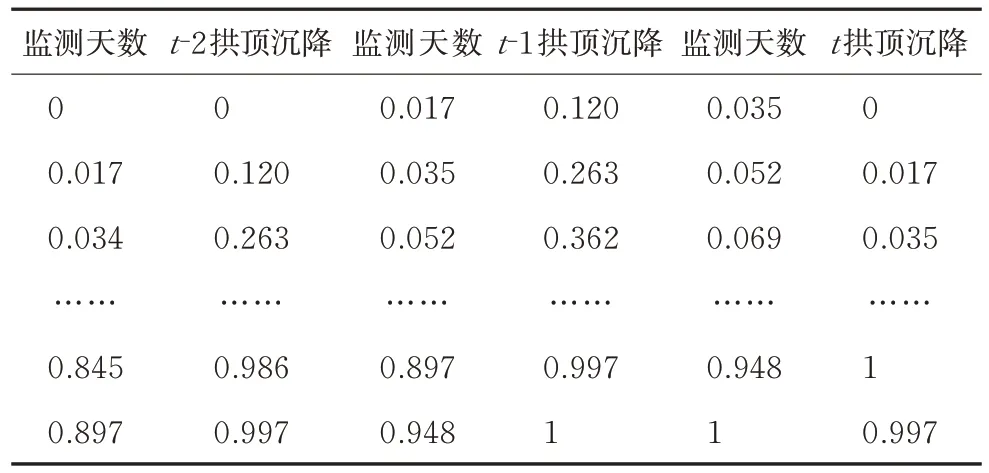
表4 C1 测点有监督数据Table 4 Supervised data of C1

分别利用Bayes-LSTM、CNN、SVR 3 个模型对拱顶沉降进行预测，并以均方根误差ERMSE（Root Mean Square Error，RMSE）为评价指标，对预测结果进行比较。

式中：yi为真实值；y^i为预测值；m为样本数量。

拱顶沉降预测对比分析结果如图6 所示，3 种模型对比结果列于图7 和表5。

表5 C1 测点沉降值与预测值比较Table 5 Comparison between settlement value and predicted value of C1

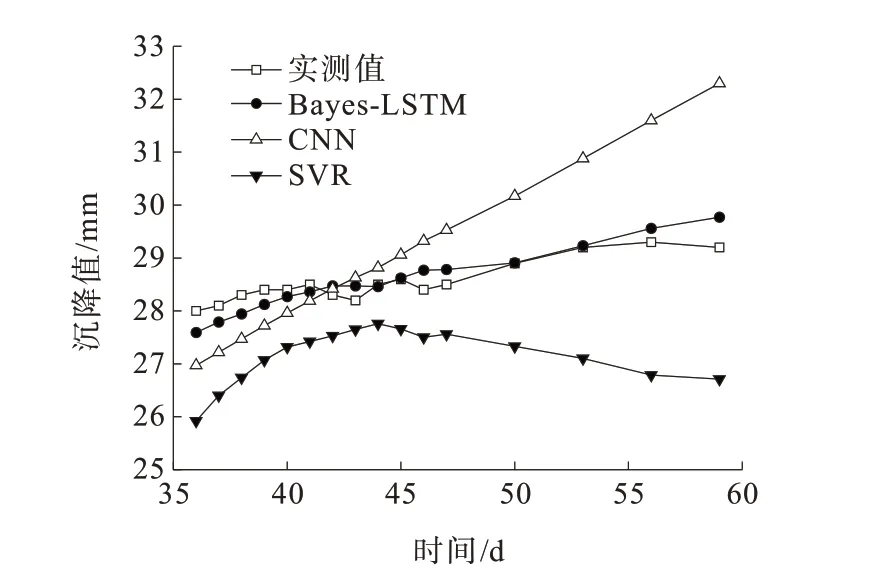
图6 拱顶沉降预测值与实测值对比曲线Figure 6 Comparison curve between predicted and measured values of crown settlement

图7 C1 测点误差对比Figure 7 Error comparison of C1

从图6 中C1 测点的沉降预测曲线可以看出：利用Bayes-LSTM 可以较好地预测拱顶沉降的变化特征。从图7 和表5 计算结果可以看出：Bayes-LSTM 网络的拟合效果优于CNN 和SVR。CNN 神经网络预测的最大误差、最小误差、平均误差、平均相对误差和ERMSE值分别为3.1 mm、0.12 mm、0.99 mm、3.43%和1.25，SVR 预测的最大误差、最小误差、平均误差、平均相对误差和ERMSE值分别为2.51 mm、0.55 mm、1.40 mm、4.87%和1.52，而Bayes-LSTM 预测的最大误差、最小误差、平均误差、平均相对误差和ERMSE值分别为0.57 mm、0.01 mm、0.23 mm、0.80%和0.28，明显看出Bayes-LSTM 网络预测效果较佳。CNN 与SVR 网络预测误差离散度较大，在多数情况下，Bayes-LSTM 预测的相对误差与残差均比CNN 和SVR 小。

针对拱顶沉降C2、C3 测点的监测数据，分别进行归一化并利用前两天数据预测第3天数据，将其转化为有监督数据，分别利用Bayes-LSTM、CNN、SVR 3个模型对拱顶沉降进行预测，结果如图8、9 所示。

图8 C2 测点拱顶沉降预测值与实测值对比曲线figure 8 Comparison curve between predicted and measured values of crown settlement of C2

由图8 可知：对拱顶C2 测点的沉降预测，CNN神经网络预测的ERMSE值为1.98，SVR 预测的ERMSE值为 1.13，Bayes-LSTM 预 测 的ERMSE值 0.33，Bayes-LSTM 网络预测效果较佳。Bayes-LSTM 网络预测误差离散程度较小，在多数情况下，Bayes-LSTM预测的相对误差与残差均比CNN 和SVR 小。

由图9 可知：CNN、SVR、Bayes-LSTM 预测的ERMSE值 分 别 为0.68、2.03、0.29。可 以 明 显 看 出，Bayes-LSTM 网络精度指标均优于CNN 与SVR，Bayes-LSTM 网络预测效果较佳。

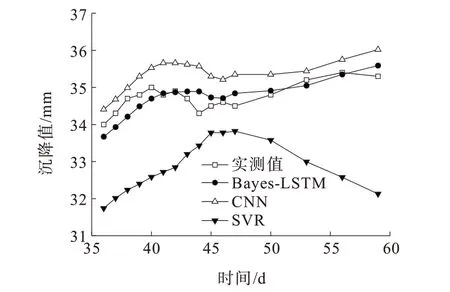
图9 C3 测点拱顶沉降预测值与实测值对比曲线Figure 9 Comparison curve between predicted and measured values of crown settlement of C3

Bayes-LSTM 模 型 针 对 拱 顶 沉 降C1、C2、C3 测点的ERMSE平均值为0.30，CNN 模型的ERMSE平均值为1.30，SVR 模型的ERMSE平均值为1.56。相较于CNN，Bayes-LSTM 的预测精度提升了1.0，相较于SVR，Bayes-LSTM 的预测精度提升了1.26。由此可见，本文提出的Bayes-LSTM 模型具有较高的可靠性。

3.2 基于Bayes-LSTM 的周边收敛预测模型与应用验证

选取此段高速公路隧道洞口开挖面（ZK58+847处）的周边收敛进行分析，其测线布置如图10 所示。

图10 周边收敛测线布置Figure 10 Layout of peripheral convergence survey lines

本监测断面周边收敛共有35 条监测数据，前15 d 监测频率为1 次/d，后20 d 监测频率为1 次/（2 d）。周边收敛的变化曲线如图11 所示。

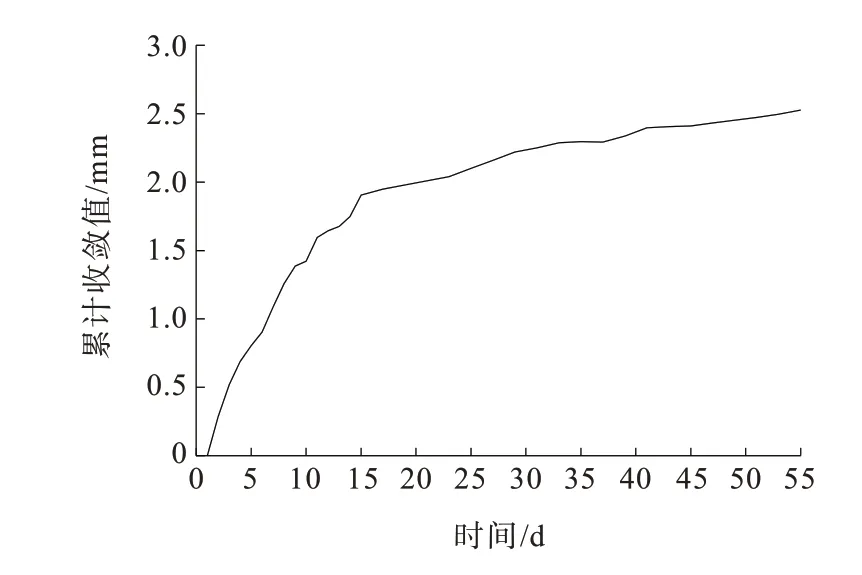
图11 周边收敛曲线Figure 11 Peripheral convergence curve

利用前67%的数据作为训练样本，用于贝叶斯优化寻找最优模型参数，后33%的数据作为测试样本进行预测，表6 为贝叶斯优化后的最优参数。

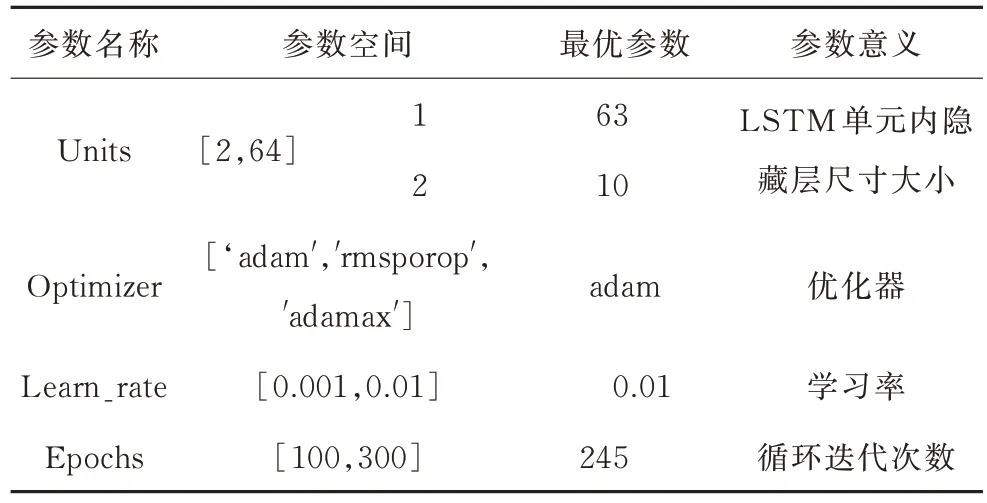
表6 最优参数Table 6 Optimal parameters

为检验Bayes-LSTM 模型的有效性，针对收敛监测数据，分别应用Bayes-LSTM、CNN 和SVR 进行预测，并将预测结果进行比较，分析对比结果如图12、13 所示，计算结果列于表7。

表7 周边收敛量与预测值比较Table 7 Comparison of peripheral convergence and predicted values

由图12、表7 和图13 可知：利用Bayes-LSTM 可以很好地拟合周边收敛的变化特征。CNN 神经网络预测的最大误差、最小误差、平均误差、平均相对误差和ERMSE值分别为0.39 mm、0.24 mm、0.33 mm、3.43%和0.33；SVR 预测的最大误差、最小误差、平均误差、平均相对误差和ERMSE值分别为0.18 mm、0.12 mm、0.35 mm、12.07%和0.35；Bayes-LSTM 预测的最大误差、最小误差、平均误差、平均相对误差和ERMSE值分别0.06 mm、0 mm、0.021 mm、0.88%和0.03。可以明显看出Bayes-LSTM 网络预测效果较佳，Bayes-LSTM 网络预测误差离散程度较小，Bayes-LSTM 具有较高的可靠性。

图13 周边收敛误差对比Figure 13 Comparison of peripheral convergence errors

从上述拱顶沉降与周边收敛的预测结果来看，LSTM 网络能够较好地拟合拱顶下沉与周边收敛的变化特征，相较于CNN、SVR，其预测结果准确性更高。

3.3 模型验证

为了验证模型的泛化能力，选取此高速公路隧道Ⅲ、Ⅳ、Ⅴ级围岩中桩号ZK58+066 等6 处断面的拱顶下沉数据和周边收敛数据进行模型验证与分析，以ERMSE为评价标准，比对结果如表8、9 所示。

表8 拱顶沉降验证结果ERMSE比对Table 8 ERMSE comparison of crown settlement verification results

表9 周边收敛验证结果ERMSE比对Table 9 ERMSE comparison of peripheral convergence verification results

对比ERMSE值可以发现：Bayes-LSTM 模型在围岩变形预测中表现较好，证明该模型具有一定的泛化能力。

4 结论

针对公路隧道施工过程中拱顶沉降和周边收敛的非线性与复杂性等特征，提出Bayes-LSTM 时间序列预测模型，构建分别针对拱顶沉降与周边收敛的模型，将数据归一化并将其转化成有监督数据，利用贝叶斯优化对超参数进行优化，计算得到预测结果，并以某高速公路隧道施工中开挖面里程ZK58+820 的拱顶实测数据和ZK58+847 周边收敛量实测数据为例，对该模型进行应用验证，得到以下主要结论：

（1） 利用Bayes-LSTM 模型进行预测时，C1、C2和C3 拱顶沉降的平均预测精度相较于CNN 模型、SVR 模型分别提高了1.0 和1.26；周边收敛的预测精度相较于CNN 模型、SVR 模型分别提高了0.3 和0.32，证明了Bayes-LSTM 模型的有效性。

（2） 基于6 个断面实测的围岩拱顶下沉数据和周边收敛数据对Bayes-LSTM 模型进行了泛化能力验证，结果显示：Bayes-LSTM 模型的ERMSE小于CNN、SVR 模型，验证了Bayes-LSTM 模型的泛化能力。

（3） 针对拱顶沉降与周边收敛变形这一复杂的非线性动态系统，提出一种基于Bayes-LSTM 算法的公路隧道围岩变形预测模型，与目前流行的预测模型相比，该模型具有以下优点：① LSTM 模型具有记忆功能，能够充分地利用围岩变形的历史数据，从而提高围岩变形的预测精度；② LSTM模型通过“三个门”对元细胞状态进行交互，能够有效实现对历史数据的判断与取舍。训练好的算法模型可以融入监测预警系统中进行工程应用，该方法为隧道围岩变形预测提供了新的思路与探索。

影响隧道拱顶沉降与周边收敛的因素是多方面的，隧道施工过程中的岩土体特性非常复杂，本文仅考虑了围岩变形不同等级的隧道变形情况，没有充分考虑地应力、岩性等特性，从而导致计算的结果与实际数据有一定的差距。此外，数据量的大小也会影响模型的预测效果。因此将会进一步采集隧道的特征参数，收集更多的训练样本，针对不同地应力、不同岩性的围岩进行进一步的研究。