基于2阶Hann自卷积窗的谐波电能高精度量测方法研究与实现

李冬,艾黄泽,尹领,曾非同,周峰

(1.华中科技大学 电气与电子工程学院,武汉 430074; 2.中国电力科学研究院有限公司,武汉 430074)

0 引 言

由于全球气候变暖和能源危机等问题的出现,能源行业不断朝着可再生能源的方向转型,以光伏发电为主的新能源装机总量逐年递增[1]。为了扶持户用式光伏和工商业光伏的发展,国家制定了相应的度电补贴标准,根据全发电量对其进行分布式光伏发电补贴[2-3]。但补贴政策没有考虑分布式光伏的供电质量,从而无法约束分布式光伏并网对配电网造成的高频次谐波污染[4-6]和电压波动[7-9]等电能质量问题。因此,研究分布式光伏的并网电能质量,可为分布式光伏电价制定提供一个参考依据,从而引导分布式光伏产业高质量、可持续发展。

输出电能谐波含量是分布式光伏电能质量的关键指标之一。目前电网主要使用时分割乘法器电子式电能表,受前端传感方式和计量算法等限制,其谐波电能计量误差在百分级[10],不适合作为电能交易策略研究的电能质量数据来源。为此,需要对分布式光伏设备中电能谐波进行单独的高精度计量与数据收集。

谐波分析常采用快速傅里叶变换(FFT)[11],但该算法应用时会存在频谱泄漏和栅栏效应的问题,进而影响谐波电能计量结果。对此,国内外学者提出了多种改进方案,包括加窗插值FFT、准同步DFT、基于小波变换的时频联合分析算法[12]、Romberg积分算法[13]等。其中,加窗插值FFT是最常用的谐波分析算法,该算法采用主瓣宽度适宜、旁瓣衰减显著的窗函数来抑制频谱泄漏,并根据所选窗函数设计频谱插值校正算法以减小栅栏效应造成的误差[14]。经典窗函数有Hann窗、Blackman窗、Nuttall窗和Kaiser-Bessel窗等[15],在此基础上有学者提出自卷积窗[16-17]、旁瓣最低与最快速下降窗[18]等改进算法,并将其应用于电力谐波分析[19-20],获得了优越的检测精度。在插值校正方面,有单峰插值和多峰插值等算法,其中双峰谱线插值校正算法[21]是电能计量领域应用最普遍的插值算法之一。

针对分布式光伏谐波电能量测装置,采用精度较高且易于实现的Hann自卷积窗与双谱线插值算法是一种合适的选择。然而,谐波电能表常采用DSP或MCU进行信号处理与分析[22-23],单核处理器对多通道多次谐波进行加窗插值FFT计算的实时性较差。

针对上述问题,本文提出了一种低运算资源消耗的顺序型谐波计算流程,并在此基础上优化设计了一种多级流水线型谐波计算架构,大幅提升了加窗插值FFT的计算效率,基于ZYNQ系统实现了2阶Hann自卷积窗及其双谱线插值校正算法。此外,考虑ADC量化误差,等效种因素的条件下开展了算法仿真实验,提供了ADC位数、采样点数N与窗函数的选择依据。最后设计并开发了基于ZYNQ与LTC2358的谐波量测装置板卡样机,并给出了量测样机的实测结果。

1 谐波算法仿真分析

1.1 2阶Hann自卷积窗及其离散化

电能谐波计量系统中,为抑制频谱泄漏对谐波参数计算带来的影响,窗函数应具有旁瓣衰减效果好、复杂度低的特点。选择2阶Hann自卷积窗对ADC采样数据进行时域截断,其频谱主瓣宽度合适、对旁瓣衰减效果优异且算法实现难度适当[16]。窗长为T的Hann窗的时域表达式为:

(1)

定义Hann自卷积窗为若干个Hann窗进行自卷积运算[16],即:

(2)

式中p表示参与卷积的Hann窗个数。通过对p个Hann窗进行p-1次卷积运算,可以得到p阶Hann自卷积窗,当p=1时,即为Hann窗本身。

以采样率fs对式(1)进行时域离散化并右移T/2后,得到长度为M=Tfs的Hann窗序列:

(3)

式中n为离散采样点的序号;M取2的整数次幂,以便于在嵌入式系统中实现该算法。根据傅里叶变换,序列(3)的频谱函数为:

ω1∈[0,2π)

(4)

序列(3)的频谱模函数为:

(5)

以频率分辨率Δω1=2π/N对式(5)进行频域离散化,得到长度为N=M的Hann窗离散频谱模序列为:

(6)

对序列(3)进行p-1次离散自卷积操作,得到长度为pM-p+1的序列,然后在卷积序列的首尾添零,得到长度为N=pM的p阶Hann自卷积窗序列。根据卷积定理,在时域上进行卷积操作等价于在频域上进行乘积操作。因此,可以由序列(6)得到p阶Hann自卷积窗的离散频谱模序列,表示为:

(7)

1.2 Hann自卷积双谱线插值算法

信号x(t)包含基波分量f0和直流分量、谐波分量,以采样频率fs对该信号进行采样,得到长度为N的离散时域序列为:

(8)

式中h表示谐波次数;Ah表示h次谐波的幅值;φh表示h次谐波的初相位。

采用2阶Hann自卷积窗对序列x(n)进行加窗处理后,其离散频谱为:

(9)

式中kh=hf0N/fs,表示第h次谐波频谱峰值点对应的谱线号。存在频率偏移时kh往往为非整数,在栅栏效应的影响下,只能利用kh附近的其他谱线进行离散频谱校正,才可确定kh的实际值,从而得到实际的频率hf0。

忽略其他谐波对第i次谐波的频谱干涉,此时,式(9)简化为:

(10)

在第i次谐波峰值点附近的局部最大值和次大值之中,记靠左的谱线号为k1,靠右的谱线号为k2,显然有k2=k1+1。记谱线校正量Δk=k1-ki,则Δk∈[-1,0]。引入参数α=Δk+0.5,显然有α∈[-0.5,0.5],且k1-ki=α-0.5,k2-ki=α+0.5。

记k1、k2两条谱线的模值分别为y1和y2,则有:

(11)

记校正系数v为:

(12)

结合式(10)～ 式(12)可以推导出:

(13)

通过式(12)可以利用y1和y2计算出校正系数v,再通过v求得α,但由于式(13)难以化简为α关于自变量v的恒等式,故可以利用MATLAB的polyfit函数,结合式(13)和式(7)对α关于v的反函数进行多项式拟合。拟合函数的阶数选择主要考虑因素是拟合精度,5阶多项式拟合函数的均方根误差RMSE=1.07×10-9,拟合程度优异,更高的阶数能够带来的拟合度提升有限,且会增大算法的工程量与处理器资源消耗,故本文采用5阶拟合函数:

α=-0.049178v5-0.062145v3-3.076222v

(14)

通过α求得谱线校正量Δk、校正后的频率f、相位φ、幅值A分别为:

(15)

1.3 考虑ADC量化误差的谐波分析仿真

实际工程中,使用ADC量化无法避免地会带来量化误差[24],在考虑ADC采样条件下对算法精度进行仿真,为后续设计提供了ADC位数、采样点数N与窗函数的选择依据。

采用MATLAB对2阶Hann自卷积窗及其双谱线插值校正算法的谐波分析效果进行仿真,其流程也可用于指导FPGA程序设计,具体计算流程如图1所示。

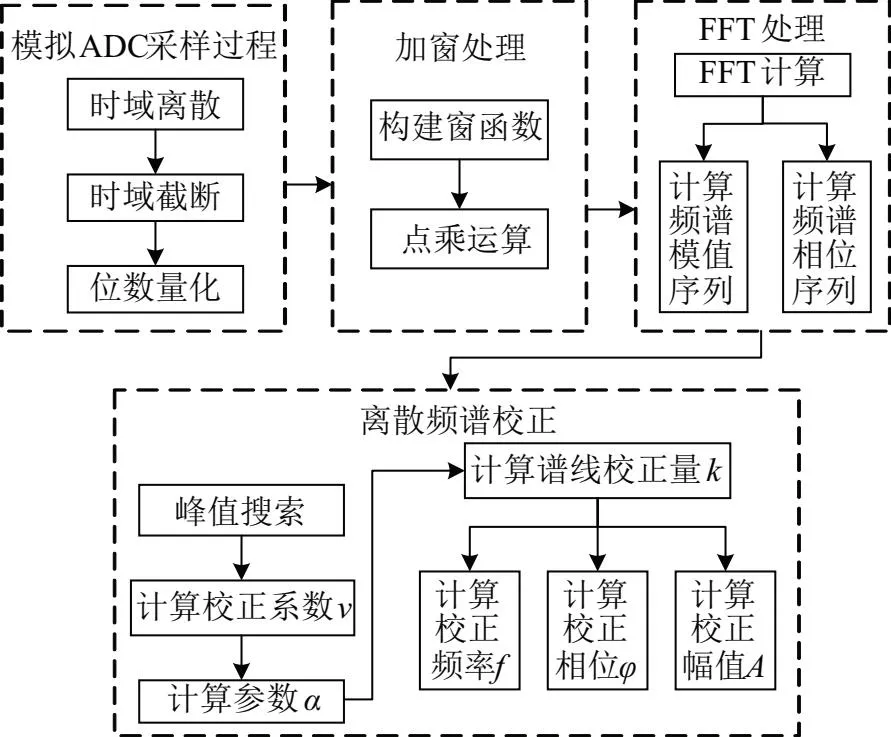
图1 MATLAB仿真程序流程图

1)模拟ADC采样过程:以采样率fs对时域连续信号x(t)进行采样离散化,截取出长度为N的离散时域序列x(n),并采用式(16)对x(n)的元素逐个处理,模拟ADC位数量化过程,得到采样序列用于谐波参数分析。

X(n)=[x(n)/K/(VIN+-VIN-)·LSB]

(16)

式中[·]代表四舍五入取整运算;K表示信号输入ADC之前的变比,以电压取样及信号处理电路为例,其变比K= 1/66;(VIN+-VIN-)表示ADC输入差分量程;LSB表示ADC的最低有效位,LSB= 2BADC,其中BADC表示ADC的位数。取整后的离散点序列需满足|X(n)|∈[0,LSB]∩Z。

2)采样序列加窗:调用MATLAB中的hann函数构造长度为N/2的Hann窗序列,进行1次自卷积操作,并在末尾添加0扩展得到长度为N的自卷积窗序列,最后将其进行幅值归一化,即得到所需的2阶Hann自卷积窗序列。将长度为N的ADC采样序列点乘长度相同的2阶Hann自卷积窗序列得到加窗后的采样数据,作为FFT模块的实部输入。

3)FFT:调用fft函数对加窗序列进行N点FFT处理,得到复数序列。然后采用abs函数处理该复数序列并乘以系数2/N得到频谱模值序列,采用angle函数处理该复数序列得到频谱相位序列。

4)离散频谱校正:确定离散频谱峰值参数,根据模值序列、频率f、采样率fs、采样点数N,采用Nf/fs计算频率f处对应谱线号的理论值,在该谱线的左右5条谱线范围内搜索,遍历找到局部最大值和次大值对应的谱线号。然后根据式(12)计算校正系数v,利用式(14)对α关于v的反函数进行多项式拟合从而计算出α,进而得到谱线校正量Δk。最后将Δk代入式(15)得到频率f、相位φ、幅值A的校正结果。

1.3.1 不同ADC采样位数时的检测误差

ADC量化给基于2阶Hann自卷积窗的谐波分析算法带来一定误差,本节改变式(16)中的LSB,对ADC量化误差造成的影响进行仿真分析,采用下述序列探究不同ADC位数对谐波检测误差的影响。

(17)

式中信号1:f1= 50 Hz、A1= 311 V、φ1= 0;信号2(弱幅值):f2= 150 Hz、φ2= π/6、A2在0.4～3.1 V之间变化,步进为0.1 V;采样率fs= 25 000 Hz,N= 8192。令ADC位数BADC分别为16、24以及MATLAB默认精度(即不考虑ADC量化)进行误差分析,其结果如图2所示。

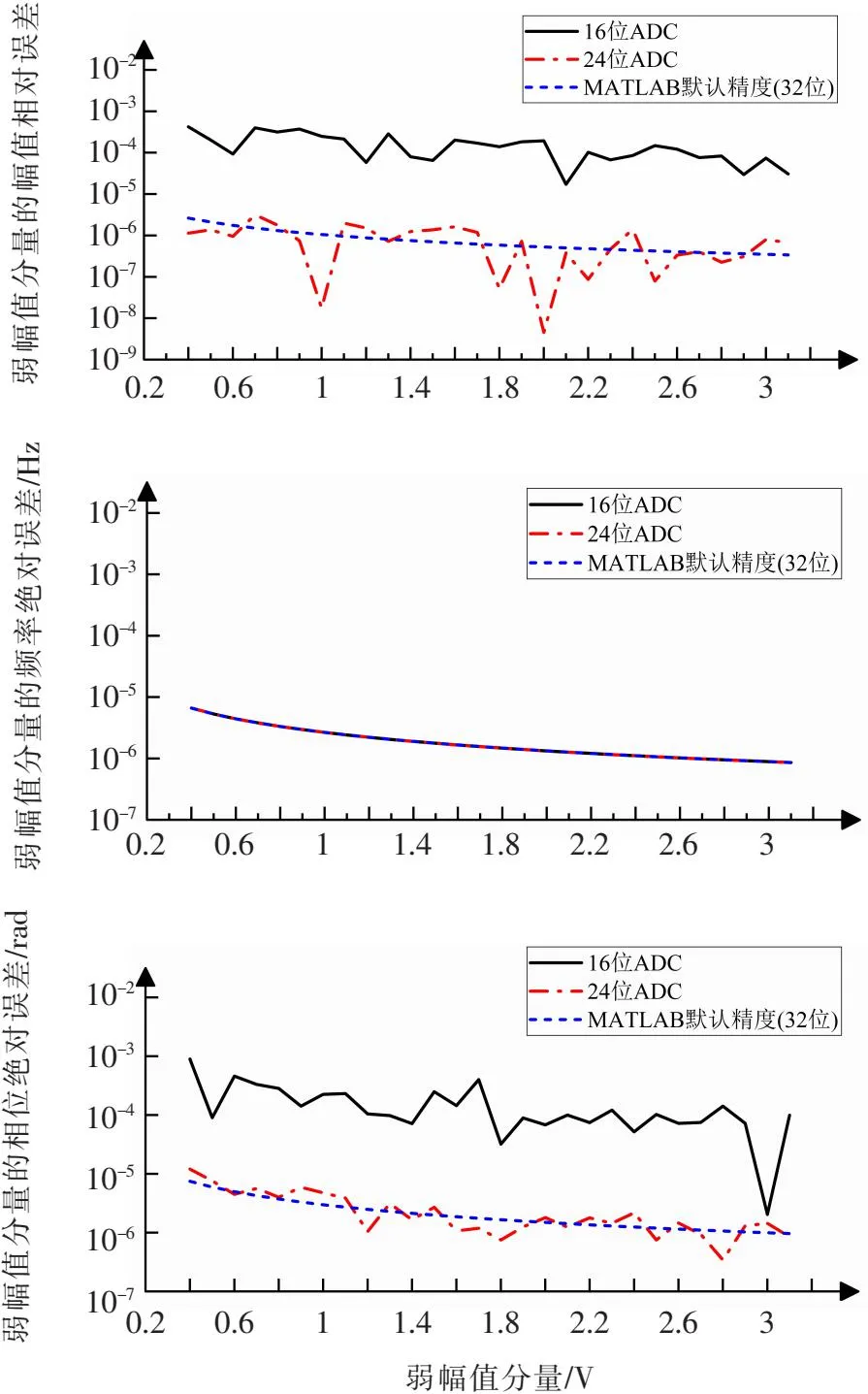
图2 不同ADC采样位数时弱信号参数分析误差

ADC采样位数的选择关系到测量系统的硬件实现成本与资源消耗。由图2可见,在MATLAB默认仿真精度(不考虑ADC量化),各参数误差曲线平滑。考虑ADC量化时,ADC位数对弱谐波信号的频率检测误差几乎无影响。但是,对于幅值和相位检测误差,采用更高的ADC采样位数能获得更高的分析精度,达到一定的ADC采样位数后,其误差精度在MATLAB默认仿真精度附近波动。说明更高的ADC采样位数能够更好地发挥算法的精度优越性,当ADC位数较低时,量化误差会导致算法的精度被ADC位数所钳制。

当BADC=16时,谐波分量的幅值相对误差在0.1%以内,相位绝对误差在0.000 5 rad以内,仍具有较高的准确度,满足本文的谐波测量系统精度需求。

1.3.2 不同采样点数N时的检测误差

针对采样点数N对基于2阶Hann自卷积窗的谐波检测误差的影响进行仿真分析,作为后续算法实现选择采样点数的依据。采用式(16)对式(17)进行量化处理。式中,信号1(基波):f1= 50 Hz、A1= 311 V、φ1=0;信号2(3次谐波):A1=10 V、f2=150 Hz、φ2=π/6。

ADC的位数选择BADC=16,取采样点数N从2 048～65 536,步进为512。对2阶Hann卷积窗对其进行谐波分析,所得各信号分量的频率、幅值和初相位分析误差随采样点数N变化的曲线如图3所示。

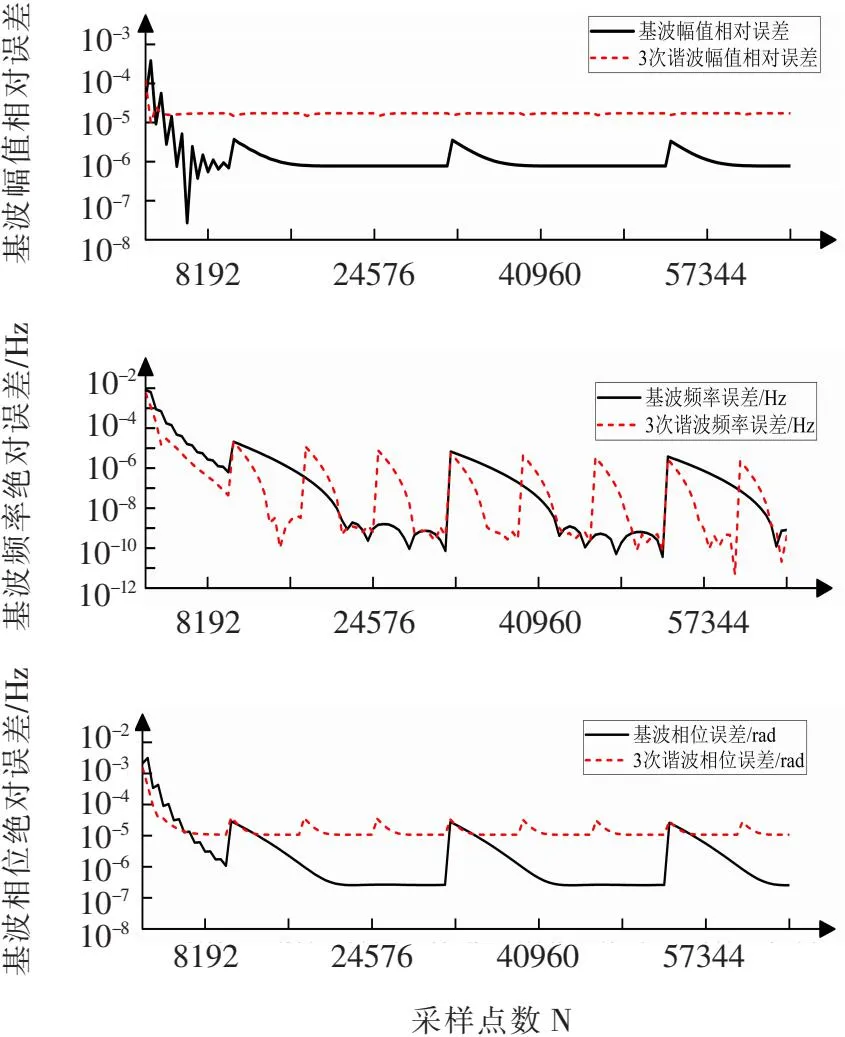
图3 采样点数N不同时谐波参数分析误差

采样点数N的选择关系到处理器的FFT计算时间与计算资源消耗大小。由图3可见在采样点数N=8 192之前,随着N增大,各信号分量的三参数误差呈减小趋势;N继续增大时,受谱线校正量Δk的波动,误差呈周期性变化趋势。

当N=8 192时幅值相对误差在0.02%以内,初相位绝对误差在0.000 5 rad以内。综合考虑算法的准确度和实时性需求,采用N=8 192较为合理。

1.3.3 不同窗函数的弱幅值信号检测误差

弱幅值谐波分量的检测精度关系到谐波电能计量的精度。当弱幅值谐波分量附近存在其它基波或谐波分量时,随着弱谐波分量相对幅值降低,其受到频谱泄漏的影响增大,参数分析的准确度会降低。Hann自卷积窗具有较好的旁瓣性能,可以很好地抑制频谱泄漏对弱幅值谐波分析的影响。本节将验证不同窗函数对弱谐波分量的参数分析效果。

采用式(16)对序列式(17)作ADC量化处理。式中,信号1:f1=50 Hz、A1=311V、φ1=0;信号2(弱幅值):f2= 150 Hz、φ2=π/6、A2在0.4～3.1 V之间变化,步进为0.1 V。取ADC的位数为BADC= 16,N=8 192。基于的Hann窗、2阶Hann卷积窗、4项3阶Nutuall窗对信号序列进行谐波分析,所得弱幅值谐波频率、幅值和初相位的误差随信号中该谐波幅值变化的曲线如图4所示。

图4 不同窗函数下弱幅值信号参数分析误差

观察图4可知,在模拟ADC采样情况下,2阶Hann自卷积窗、4项3阶Nutuall窗的弱幅值分量的幅值、相位误差相比于Hann窗降低了2个数量级;频率误差相较Hann窗降低了4个数量级。其中,2阶Hann自卷积窗、4项3阶Nutuall窗误差曲线重合的原因是ADC位数钳制了算法发挥更高的分析精度。

2 谐波量测装置硬件设计

谐波量测装置板卡样机的硬件框图如图5所示,主要由电流传感器及信号处理电路、电压取样及信号处理电路、模数转换器(ADC)、ZYNQ控制器与三相载波模块构成。谐波量测装置从光伏系统的三相节点上对电压电流进行取样与处理,通过ADC采样并通过ZYNQ进行谐波分析与计算,将得到的电能结果通过载波模块发送给电能采集终端。

图5 谐波量测装置硬件框图

谐波量测装置的硬件设计核心在于数据采集单元和数据处理单元。首先,考虑谐波测量的精度问题,且系统需具备采集从直流到高次谐波信号的能力,数据采集单元的ADC与传感器选型十分重要;其次,由于系统的多通道多次谐波的快速计算与数据实时上传需求,主控制器的选型也较为关键。本文将重点介绍这两个方面的硬件设计与选型思路。

2.1 数据采集单元

由于量测装置需具有50次以内的谐波分析能力,根据奈奎斯特定理可知ADC采样率应在5 ksps以上,为了留有足够的裕度,故选择最高采样率在25 ksps以上的ADC;考虑ADC的量化误差,根据装置的准确度等级要求,应选择13位及以上的ADC。综合考虑准确度和硬件实现成本,选用LTC2358-16,它是一款16位8通道同步采样ADC,每通道最高采样率200 ksps。

电流传感器选型主要考虑可测信号的幅值范围、频率范围、测量精度、1 min绝缘耐压等级等参数。CSA101-G050T01电流传感器可将幅值±100 A的一次电流转换为±50 mA的二次电流,信号频率范围0～100 kHz,测量精度0.02%,1min绝缘耐压5 kV,符合取样器选型要求。电压取样装置由电阻分压器与抗混叠滤波器组成,其中分压器的低压端电阻与并联电容共同组成抗混叠滤波器对信号进行滤波。

2.2 数据处理单元

数据处理单元选型需考虑谐波电能的实时性计算,FPGA作为可编程逻辑器件,具有高速、并行运行及设计灵活等优势,相较于MCU与DSP更适用于多通道多次谐波的大计算量使用场景。本文选用Zynq7000系列芯片作为主控制器,型号为XC7Z035-2FFG676,该芯片集成了FPGA可编程逻辑和ARM处理器,基于AXI总线协议实现ARM与FPGA之间的高效片内互联。FPGA用于实现ADC数据采集、数据缓存、卷积窗FFT与离散频谱校正等功能;ARM用于实现原始电能数据的解析计算、载波通信等功能。

3 谐波分析程序架构设计与实现

基于ZYNQ的谐波分析程序整体设计框图如图6所示,主要分为数据采样缓存模块、谐波分析模块与BRAM数据交互模块。

图6 谐波分析程序整体框图

数据采集缓存模块将6个通道的ADC采数据存入FIFO中,在接收到FFT处理完成标志位时,开始将FIFO数据依次写入FFT数据处理模块进行加窗、FFT与离散频谱校正。所得到的6个通道校正后的幅值频率相位数据通过BRAM存储控制模块与内置ARM进行数据交互,然后在ARM内完成数据的解析与载波发送。

由于系统需进行多电压电流通道的多次谐波参数计算,在保证参数测量精度的同时要做到高时效性。所以,谐波分析模块的数据链路设计与程序架构设计合理性尤为重要。本节着重介绍谐波计算的数据链路设计与谐波计算架构。

3.1 谐波分析模块数据链路设计

谐波分析模块的数据链路如图7所示。为了降低FPGA计算带来的量化误差与截断误差,在计算资源合理需求的范围内对各个寄存器变量选取合适的位数。

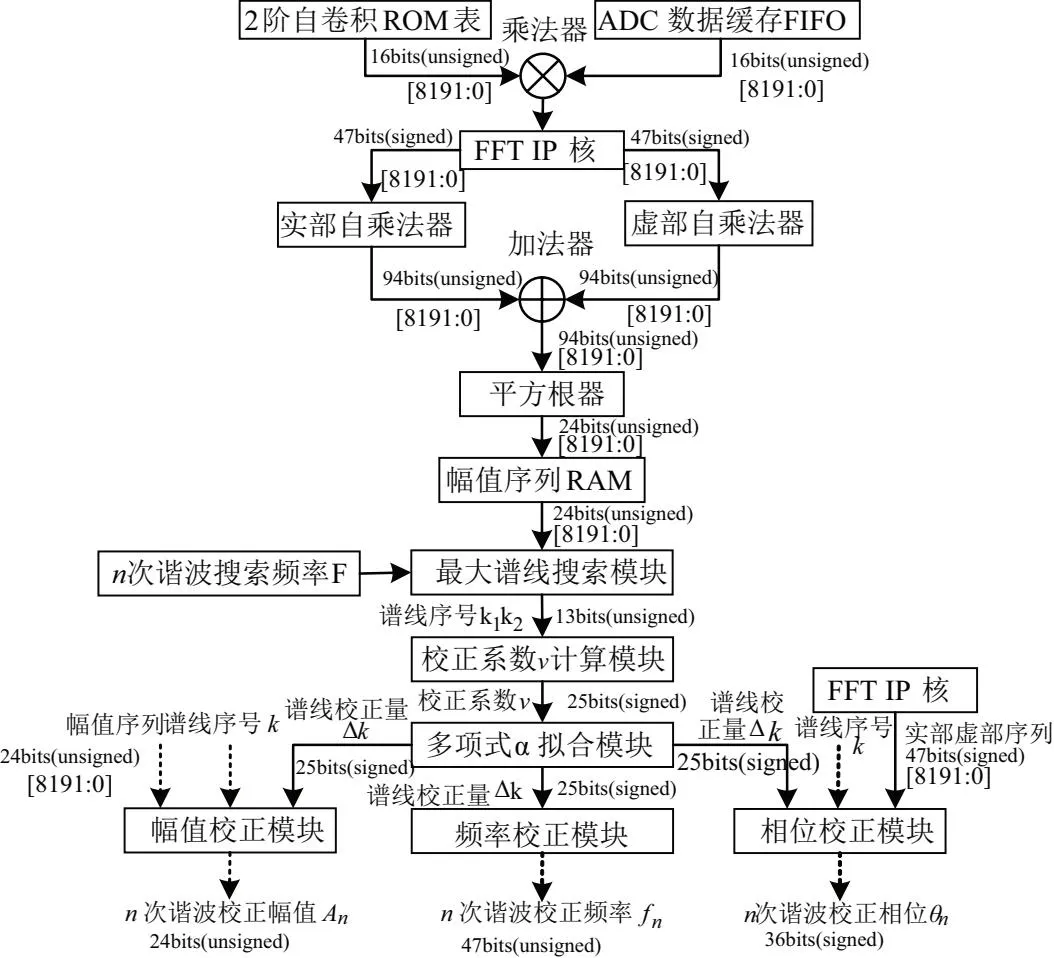
图7 谐波分析模块数据链路图

首先由FIFO缓存的ADC数据通过乘法器与Hann自卷积ROM表进行点乘;乘法器输出数据流给FFT IP核,经过FFT计算输出的实部与虚部结果分别通过自乘法器、加法器与平方根器,得到原始FFT输出数据的幅值序列谱。

基于幅值序列谱,在n次谐波理论频率附近±5根谱线的范围依次进行峰值和次大值谱线搜索,得到各频率的谱线号k1、k2和对应的模值y1、y2;根据式(12),利用y1、y2计算校正系数v;接下来采用式(14)的多项式拟合α关于v的反函数,进而根据α=Δk+0.5得到谱线校正量Δk;根据式(15),分别构造幅值、频率、相位校正模块,将谱线校正量Δk、谱线序号k1、k2、幅值序列、实部虚部序列输入对应的校正模块中,求得n次谐波的各项校正参数。

3.2 谐波分析模块程序架构设计

3.2.1 顺序型谐波计算流程

多通道ADC数据实现加窗、FFT与离散频谱校正功能若实例化多个同一功能的模块进行计算将耗费大量LUT资源。为此,设计一种顺序型谐波计算流程,如图8所示。多通道ADC数据分通道进行谐波处理,顺序型谐波计算同一时间只能处理ADCm通道的第n次谐波,处理完毕后再进行下一次谐波的处理,直到6路ADC通道的50次谐波均处理完毕,才开始下一时刻点的ADC采样序列谐波计算。

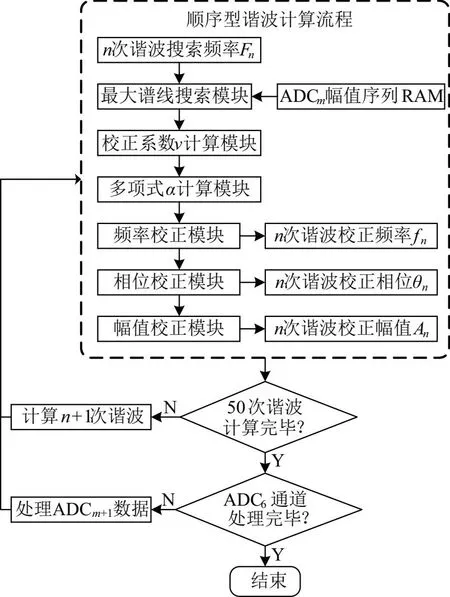
图8 顺序型谐波计算流程

3.2.2 多级流水线型谐波计算架构

低资源消耗的顺序型谐波计算需要逐次谐波、逐模块进行计算,将耗费大量时间。为发挥FPGA并行计算的优势,在顺序型计算流程基础上优化设计了一种多级流水线谐波计算架构,可显著提升多次谐波的计算效率。如图9所示,多级流水线谐波计算架构由各个子模块流水线组成。当ADCm通道的谐波计算开始时,频率输出流水线首先将基波搜索频率F1输出给谱线搜索流水线,谱线搜索流水线在计算出基波谱线号k1、k2后输出给校正系数v流水线,并将谱线搜索完毕标志置1,获取下一次谐波的搜索频率F2并等待v计算完毕标志拉高再开始下一次谐波谱线号的输出。

若校正系数v流水线已将v计算完毕标志拉高,而谱线搜索流水线未完成下一次谐波的计算,那么校正系数v流水线将等待谱线搜索流水线的输出有效信号拉高时再开启下一次计算。其余流水线的计算模式均同上。

3.2.3 子模块状态机设计

谐波计算架构的各个子模块均采用状态机的逻辑结构实现,以校正系数v计算模块为例说明本文状态机的设计方法,如图10所示。在校正系数计算环节,首先进入radio_Init状态,此状态下将各变量置0,并基于最大谱线搜索模块计算得到的k1、k2;接下来进入radio_On状态,此状态下延迟计数变量cnt会在每个时钟上升沿自加1,当cnt∈[2,6]时,读取幅值序列RAM中k1、k2所对应的模值y1、y2,并且根据式(12)计算被除数与除数;当cnt∈[7,8]时,将被除数与除数输入给除法器IP核进行计算;最后进入radio_Finish状态,等待除法器的valid标志位置1,保存除法器的输出结果存入寄存器变量,等待下一次计算流程开始。

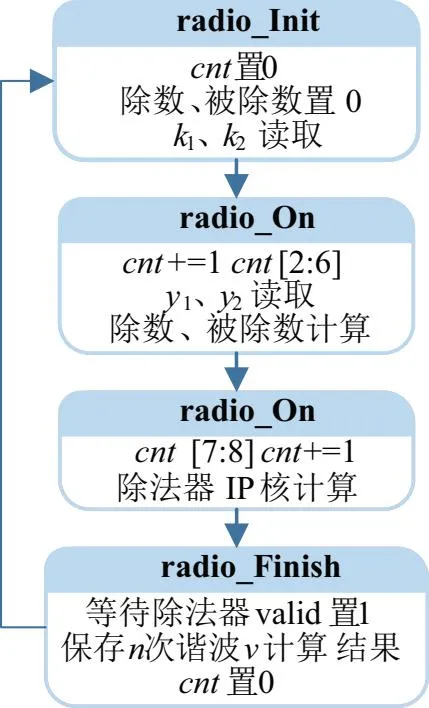
图10 校正系数v计算状态机流程图

4 实验与测试

基于0.05级电子式互感器检测平台和PA8000系列功率分析仪对量测装置板卡样机的计量准确度进行测试,测试环境如图11所示。其中,0.05级电子式互感器检测平台作为功率源,输出符合测试条件的电压、电流给功率分析仪和量测装置;PA8000功率分析仪作为标准测量仪表,基本精度为0.01%,测量带宽为直流和0.1 Hz～5 MHz交流,将其测量结果作为标准值与量测装置样机的实测值比较,得到量测装置样机的误差。

图11 量测装置测试平台

4.1 基波测量误差

根据C级静止式有功电能表标准[25]、0.5 S级静止式基波频率无功电能表标准[26]及相应的交流电测量设备试验标准[27],对量测装置样机进行电流改变与频率偏移引起的功率误差测试。

受限于0.05级电子式互感器检测平台输出电压上限为200 V,电流上限为40 A,下限为0.14 A的限制。将测试参数设置为:基波电压为200 V、额定电流Ib= 40 A、转折电流Itr= 1 A、最小电流Imin= 0.24A、启动电流Ist= 0.14 A。

电流改变引起的误差测试、频率偏移引起的误差测试结果分别如表1、表2所示。

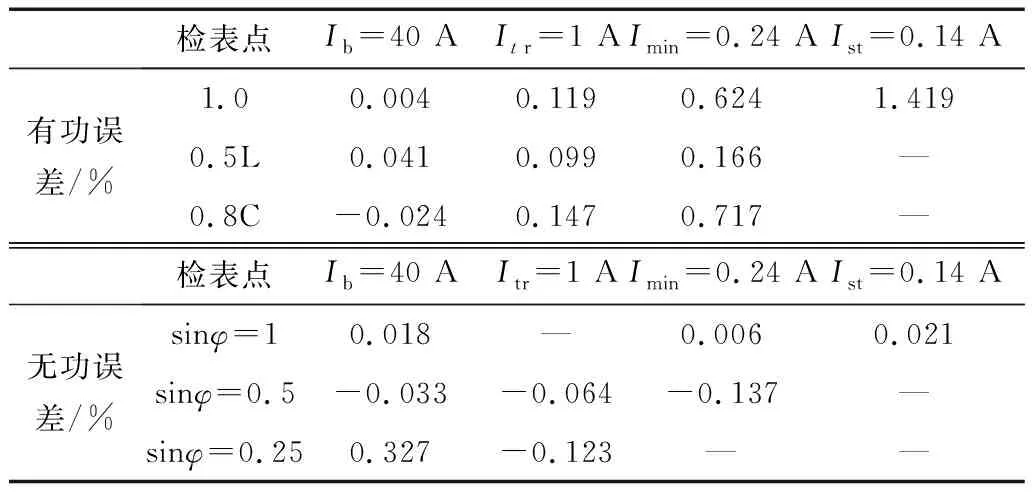
表1 不同电流情况下的功率测量误差

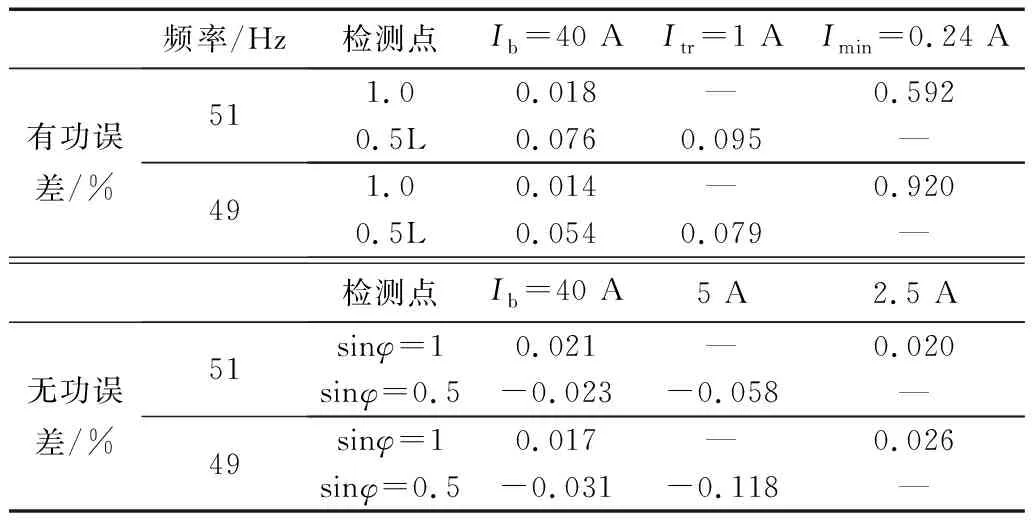
表2 不同频率下的功率测量误差

测试结果表明,样机的基波测量准确度满足C级静止式有功电能表标准与0.5 S级无功测量仪表检定标准的要求。观察测试结果可知,在两种测试条件下,均存在电流低于Imin时误差显著增加的现象,考虑是较小电流的条件下ADC采样幅值较小,实际电路引入的噪声干扰与FPGA算法实现过程中的位数截断问题显著增加了参数测量误差。

4.2 谐波测量误差

根据公用电网谐波标准[28]和光伏系统并网技术要求[29],对量测装置样机进行谐波测量准确度测试,设置基波电压200 V,基波电流40 A,包含3～21奇次谐波,各次谐波的电压、电流含量如表3所示,其中h为谐波次数,uh为谐波电压相对基波电压的比值,ih为谐波电流相对基波电流的比值。测试结果中,3～21次奇次谐波的电压、电流幅值相对误差和电压、电流相位差如表4所示,结果表明,量测装置样机的谐波准确度满足A级谐波测量仪表检定标准的要求。

表3 测试信号的各次谐波含量

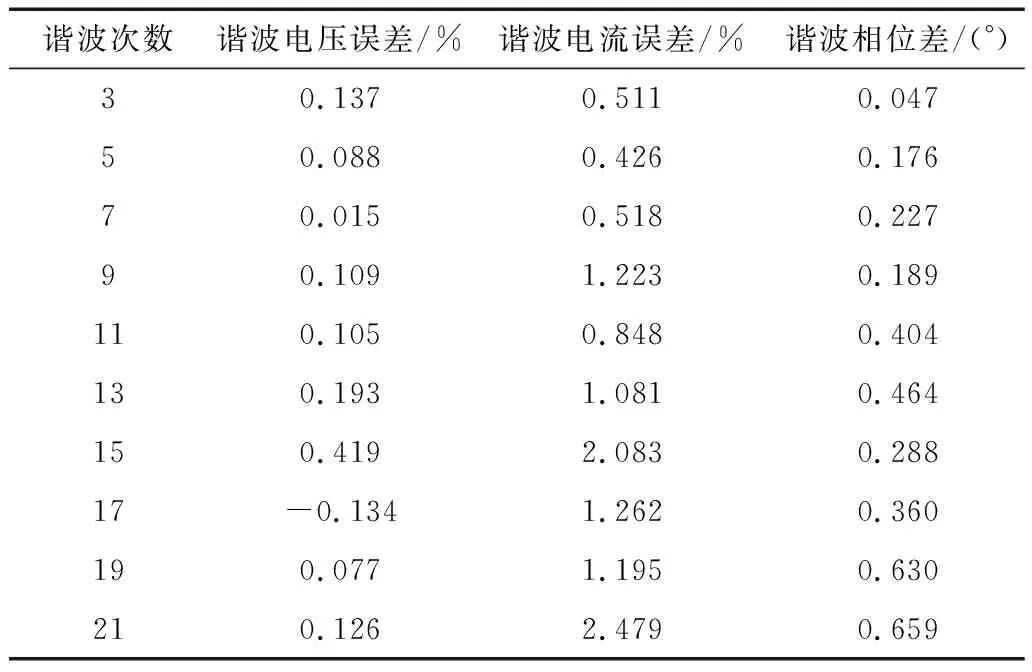
表4 谐波测量误差结果

其中,15～21次谐波参数的相位角误差增大,考虑是取样电路无源滤波器在不同频率下的相移所导致;幅值误差增大是由于实际电路引入的噪声干扰与FPGA算法实现过程中截断误差共同影响所致。可考虑采用更高位数的ADC,并对取样信号输入通道设计多挡位放大切换功能将弱谐波信号放大后采样,进而提高谐波检测精度。

5 结束语

本文提出了一种多级流水线型的谐波计算架构大幅提升了加窗插值FFT的实时计算效率,基于ZYNQ系统实现了2阶Hann自卷积窗及其双谱线插值校正算法。考虑ADC量化误差,对2阶Hann自卷积窗及其双谱线插值校正算法的谐波分析效果进行仿真,提供了ADC位数、采样点数N与窗函数的选择依据。基于ZYNQ与LTC2358,设计并开发了谐波量测装置的板卡样机。经实验测试,样机的基波测量误差满足C级静止式有功电能表标准与0.5S级无功测量仪表检定标准的要求。此外,谐波测量误差结果显示该样机的准确度满足A级谐波测量仪表检定标准的要求。