基于加窗插值压缩感知的谐波/间谐波检测方法

杜太行,梁倩伟,孙曙光,王景芹

(1.河北工业大学 人工智能与数据科学学院,天津 300130;2.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室,天津 300130)

0 引 言

随着智能电网的快速发展,以风电、光伏为代表的可再生能源设备规模化接入电网,大量的电力电子设备和冲击性负荷投入使用,导致电网中谐波/间谐波含量大量增加,使得电能质量问题日益突出[1]。

传统的谐波/间谐波检测方法建立在奈奎斯特采样定理之上,要求采样频率不小于信号中最高频率的2倍,而谐波间谐波的检测逐步趋向于复杂化和常态化,如若需要长时间对谐波/间谐波进行实时检测,将会产生庞大的数据量,对数据的存储、传输,以及硬件的要求都产生了极大的挑战[2]。而压缩感知理论的提出,打破了传统采样定理的限制,该理论实现了信号压缩和采样的同步进行,为信号处理和图像识别等领域开辟了新的方法。

将压缩感知应用到信号处理中的前提是信号本身或在某个变换基下是稀疏的,但是在傅里叶变换基下得到的稀疏信号是傅里叶变换的频域信息[3],在对谐波畸变信号压缩采样时,非同步采样和频率波动造成的频谱泄漏和栅栏效应同样无法避免,可能会对检测结果造成较大的影响。

为采用压缩感知算法实现谐波/间谐波的高性能检测,文献[4]提出一种SACoSaMP算法,该算法能够在谐波信号稀疏度未知的情况下,在重构的稀疏向量基础上实现谐波信号的检测,但并没有考虑含有间谐波的情况;文献[5]首先对信号进行加窗FFT变换,得到高稀疏度的信号,然后采用基波滤除的多谱线插值修正的谱投影梯度算法对谐波信号进行重构,并未直接对谐波信号参数进行检测;文献[6]提出构造窗稀疏测量矩阵,利用多重提取梯度追踪算法进行重构,将基波、谐波和间谐波分阶段提取检测,实现了谐波信号的高精度检测,但是该方法较为繁琐;近年来,文献[7]提出一种加六项五阶余弦窗的FFT算法,采用四谱线插值实现了对谐波/间谐波的高精度检测。

文章提出一种加窗插值CS算法,利用六项五阶组合余弦窗和二进制稀疏测量矩阵构造新型窗稀疏测量矩阵,降低在傅里叶变换基下对谐波畸变信号变换时频谱泄漏的问题,然后采用SACoSaMP算法对稀疏向量进行重构,利用四谱线插值修正公式对谐波/间谐波参数进行校正,通过MATLAB仿真,与加六项五阶组合余弦窗,四谱线插值的FFT(SF-FFT)进行比较,验证了文章所提方法的检测性能。

1 压缩感知理论

压缩感知理论的本质是一种非线性的可压缩信号的重建算法,当信号x为稀疏信号时,其线性表达式为:

y=Φx

(1)

式中x为原信号;Φ为M×N维的测量矩阵;y为N×1维的观测向量。

实际工程中绝大多数信号并不是稀疏的,但是一般能够找到特定的变换基Ψ,使得信号在该基的投影下呈现出所需的稀疏性,即:

x=Ψθ

(2)

Ψ为N×N的变换基,此时可得观测向量为:

y=ΦΨθ=Aθ

(3)

A为M×N维的传感矩阵,此时为保证能够完整地对信号进行重构,必须满足两个特性[8]:Φ和Ψ不相关;传感矩阵A满足约束等距特性。即:

(4)

式中δK∈{0,1},称为约束等距常数,即当满足RIP时,δ取得的最小值。目前常用测量矩阵有高斯随机测量矩阵,伯努里随机测量矩阵、部分傅里叶随机矩阵等。

由式(3)求解θ是一个求解欠定方程组的问题,但是当传感矩阵满足RIP,可以将求解欠定方程组的问题转化为最小l0范数的问题,即:

(5)

最小l0范数优化求解是NP-hard问题[9],因此诸多学者对此进行了改进,其中最为常用的有两种:一种是将该问题转变为凸优化问题;另一种是基于l0的贪婪算法。由于贪婪算法计算速度快,计算量小,容易实现,且工程中的谐波检测趋于复杂化和密集化,所以文章选取贪婪算法作为重构算法。

2 基于加窗插值CS的谐波/间谐波检测方法

2.1 窗稀疏测量矩阵

传统FFT算法在处理频谱泄漏问题时,大都采用加窗插值的方法。其中较为常用的窗函数hanning窗,hanmming窗,Blackman窗以及Nuttall窗等[10],插值算法一般采用双谱线插值、三谱线插值以及多谱线插值。

文章综合六项五阶组合余弦窗良好的频谱集中特性,以及二进制稀疏测量矩阵复杂度低,易于在硬件上实现的特点,提出一种新型窗稀疏测量矩阵,实现压缩感知算法在测量矩阵上的改进。

其中组合余弦窗时域表达式为:

(6)

式中n=0,1,…,N-1;N为谐波信号长度,a0=0.262 473 306 8;a1=0.426 559 583 2;a2=0.225 056 343 8;a3=0.072 699 592 1;a4=0.012 512 095 8;a5=0.000 782 570 1。

由式(1)可得:

y=Φx′=Φ(w∘x)=ΦWSMx

(7)

式中“ ∘ ”表示哈达码乘积;x′为加窗后得到的信号;w为离散化窗序列;x′,x,w均为N×1维向量;Φ为二进制稀疏测量矩阵;ΦWSM窗稀疏测量矩阵。

由此可得窗稀疏测量矩阵表达形式:

ΦWSM=[(φ1∘w)(φ2∘w)…(φM∘w)]T

(8)

2.2 SACoSaMP重构算法

SACoSaMP算法是在CoSaMP算法基础上的改进,通过结合CoSaMP的回溯思想和SAMP自适应调节步长逼近信号稀疏度的特点,可以在原谐波信号稀疏度未知的情况下将谐波参数检测出来。其步骤如下:

步骤1:初始化各数据r0=y,Λ0=φ,A0=φ,J0=φ,t=1,s=1。

步骤2:计算u=abs [ATrt-1],选取u中最大的2s个元素,将其对应A中的列序号j构成集合J0。

步骤3:更新索引集Λt和支撑集At,Λt=Λt-1∪J0,At=At-1∪αj(j∈J0)。

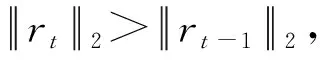
其中r0为初始残差;Λt为t次迭代的索引集;aj为传感矩阵A的第j列;At={aj} (j∈J0)为初始支撑集;t为迭代次数;s为步长。为提高计算的准确性,将初始步长设为1。

2.3 插值修正公式

经过SACoSaMP算法重构出稀疏向量后,由于栅栏效应,实际的谱线并没有位于谱线分辨率的整数倍上。利用四谱线插值修正,可以根据离真实谱线最近的四条谱线,准确估计出真实的幅值,原理如图1所示。

图1 四谱线插值原理

其修正公式[7]为:

(9)

式中fs为采样频率;fi,ai,φi分别为所求的频率,幅值和相位;ki为离峰值最近的次大谱线;yi-1,yi,yi+1,yi+2为四个谱线对应的峰值;δ为偏移量,且有δ∈[-0.5,0.5],通过多项式拟合,能够得到中间变量δ和u(δ)的近似表达式:

δ=3.19150102858672β+0.634316803314208β3+0.297984182782785β5+0.188585104878528β7

u(δ)=1.50956630632282+0.220537236245935δ2+0.0171187895020846δ4+0.000957569490375155δ6

其中β为:

(10)

经以上分析,基于加窗插值CS谐波间谐波检测方法流程如图2所示。

图2 加窗插值CS算法流程图

3 仿真分析

3.1 稀疏性分析

假设含有谐波的电力信号为:

(11)

该谐波信号包含频率为50.2 Hz的基波、2次谐波以及两个间谐波分量,参数如表1所示。

表1 给定谐波/间谐波信号参数

设采样频率设为5 120 Hz,采样时长为0.2 s,得到N维采样序列,给定压缩比C=0.25,采用M×N维的窗稀疏测量矩阵对采样得到的数据进行观测,得到压缩后的M维采样数据,其中M=C×N。得到的原始谐波信号采样序列,以及压缩采样后序列如图3和图4所示,文章通过这种方式来模拟压缩采样过程。

图3 原始谐波信号

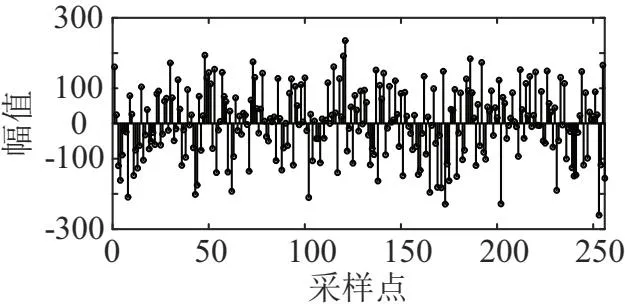
图4 压缩后谐波信号

其中压缩比表达式为:

(12)

利用WI-CS算法,分别在加窗和无窗情况下,对稀疏向量进行重构,观察稀疏向量的稀疏性,结果如图5所示。

图5 重构稀疏向量对比

根据DFT性质可得,在没有发生频谱泄漏的情况下,稀疏向量的稀疏度应为谐波分量的2倍,但从图5可以看出,两种情况下的稀疏度都远大于8。由此可以证明,谐波畸变信号在DFT基下变换后会产生泄漏。

从图5还可以看出,无窗情况下重构的稀疏向量旁瓣衰减较缓,泄漏的频谱充满整个稀疏向量,若直接进行检测,则会直接影响稀疏度的判断,也就无法实现谐波间谐波的准确检测,而基于WSM的压缩感知算法,能够使稀疏向量的能量更集中,并且旁瓣能够快速衰减为0,能够保证所需的稀疏性,进而结合图1所示的四谱线插值,实现在较少数据的情况下完成谐波/间谐波的检测。

3.2 算例1

对压缩比为0.25的WI-CS与SF-FFT进行仿真分析,仿真次数为50次,以各参数检测相对误差的平均值作为评价指标,又因为在泄露情况下,重构的稀疏向量的元素个数远大于8,尽管采用四谱线插值,对谐波分量的个数判断也有可能产生错误,所以引入检测成功率的概念,即检测的结果中没有多余分量的情况。得到的结果如表2所示。

表2 算例2检测结果

由表2可知,随着谐波/间谐波频率的增大,WI-CS的幅值和频率检测精度都有所下降,这是因为谐波/间谐波次数越大,谐波分量的能量就越小,更容易受到干扰分量的影响。当压缩比为0.25时,WI-CS的检测成功率为100%,并且SF-FFT和WI-CS算法都能达到较高精度。此时采样频率为5 120 Hz,SF-FFT需要采样的点数高达1 024,而由图4可知,WI-CS的采样数据量仅为256,相当于将采样频率降低为原来的四分之一。这是由于WI-CS的采样呈现出随机性,尽管采样序列的数量较低,但是在测量矩阵满足RIP条件时,采样序列能够保留信号的大多数有用信息,通过重构算法能够得到稀疏向量,最后利用四谱线插值修正公式,来改善对稀疏度的估计。

3.3 算例2

压缩比作为重构算法的重要参数,决定了采样序列的长度,影响着压缩后的观测向量中,包含原谐波信号重要信息的多少,所以本节对不同压缩比下的WI-CS进行分析。仍采用表1给定的谐波参数,压缩比分别为0.2,0.3,0.4,0.5,其他参数设定值同算例1,利用文章算法进行检测,得到的幅值、频率、相位检测相对误差如图6所示。

图6 各参数检测相对误差

如前面分析,WI-CS的幅值和频率检测相对误差较小,为更加直观地体现出检测结果的差异,将其图形的纵坐标按照检测相对误差的对数刻度进行显示。由图6可知,随着压缩比的不断增大,WI-CS 的幅值和频率检测精度逐步得到提升,当压缩比大于0.4时,检测精度趋于稳定,这是因为压缩比提高到一定程度后,压缩采样序列中能够涵盖谐波信号的大部分有用信息,对重构的稀疏向量进行插值计算得到的检测精度趋于稳定。而相位检测相对误差相对于上述两个参数,受压缩比变化的影响较小,基本保持不变。当压缩比大于0.2时,WI-CS的幅值检测相对误差不超过5.6718×10-4%、频率检测相对误差不超过1.0143×10-6%、相位检测相对误差不超过1.2991×10-2%,并且仿真表明,其检测成功率均为100%。与表2对比可知,当压缩比达到0.4时,WI-CS的检测精度与SF-FFT相当,此时压缩感知所需处理的数据仅为SF-FFT的0.4倍,在很大程度上提高了谐波间谐波的检测效率。

3.4 算例3

在实际谐波检测中往往伴随着环境噪声,影响方法的检测结果,本节主要分析在表1的谐波信号中添加60 dB和70 dB高斯白噪声后,对方法检测结果的影响,以此来分析方法的抗噪性。压缩比设为0.25,实验次数为50次,求取其平均值作为检测结果。检测结果如表3和表4所示。

表3 60 dB下谐波检测结果

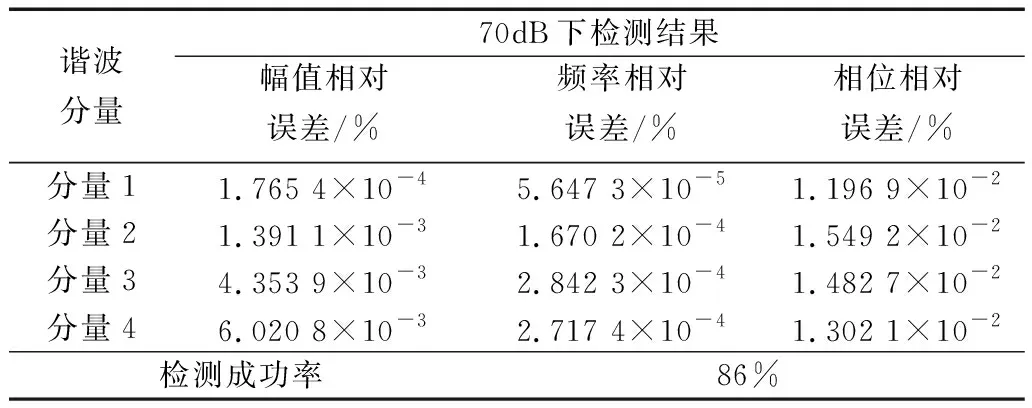
表4 70 dB下谐波检测结果

根据表3和表4可知,在噪声的影响下,重构的稀疏向量中会出现大量干扰分量,导致WI-CS的检测成功率下降,检测精度也有所影响。但当加入60 dB和70 dB高斯白噪声后,其检测相对误差仍能够保证在1.568 4×10-2%以内,并且平均检测成功率能够达到82%,表明该方法具有可行性。

4 结束语

文章结合余弦窗和二进制稀疏测量矩阵,构造出一种新型窗稀疏测量矩阵,然后通过重构算法重构稀疏向量,利用四谱线插值实现了基于WI-CS的谐波/间谐波的准确检测。

经实验分析表明,文章方法克服了压缩感知中,使用傅里叶变换基而产生频谱泄露的问题,并且相对于常规检测方法,WI-CS在具备较高检测精度的前提下,降低了所需采样数据量,当压缩比为0.25时,WI-CS的检测相对误差可以控制在1.234 4×10-2%以内,检测成功率为100%;且在噪声条件下,WI-CS的检测成功率能够达到80%以上,检测相对误差控制在1.568 4×10-2%以内,具有可行性。综上,文章方法解决了非同步采样下,压缩感知用于谐波检测时,无法准确检测出谐波分量个数,以及检测精度不足的问题,提高了该方法的适用范围。