陶瓷球为磨矿介质的立式搅拌磨磨矿特性研究

2024-03-21薛玉君李济顺卢志浩

矿山机械 2024年3期

关键词：陶瓷球搅拌器磨机

刘俊，刘伟，薛玉君，程波，李济顺，卢志浩

1洛阳矿山机械工程设计研究院有限责任公司河南洛阳 471039

2智能矿山重型装备全国重点实验室河南洛阳 471039

3河南科技大学河南省机械设计及传动系统重点实验室河南洛阳 471003

4河南科技大学机电工程学院河南洛阳 471003

5中信重工机械股份有限公司河南洛阳 471039

近年来，易选的矿产资源逐渐减少，随着我国“双碳”战略进一步深化，面对有限的矿产资源，增加其利用率成为重中之重。立式螺旋搅拌磨作为一款超细磨设备，能够满足传统球磨机无法达到的研磨粒度要求，且能量利用率更高，节能效率可提高 30%～50%[1]，是实现“绿色矿山”的重要设备之一。

研磨介质作为磨机中靠自身的冲击力和研磨力将物料粉碎的载能体，是磨机的重要组成部分之一。在磨矿生产中，尽可能地发挥研磨介质的功能是提高磨机效率的最关键因素，因此，研究研磨介质与磨矿特性的关系意义重大。国内外很多学者对此进行了研究，Sinnott 等人[2-3]通过离散单元法对具有螺旋搅拌器与棒形搅拌器的立式磨机进行研究，发现螺旋搅拌磨和棒式搅拌磨内钢球运动呈现不同趋势，并且非球形介质会恶化搅拌器的磨矿效果，增加搅拌器的磨损；Strobel 等人[4]研究了在小型卧式搅拌磨机中，研磨介质尺寸和流体黏度对物料应力状态的影响，结果表明，较大的磨粒可得到较高的应力能，而黏度的增加会降低应力能；Batjargal 等人[5]对搅拌球磨机磨矿介质的三维运动进行了数值模拟，计算了磨矿介质的受力、动能和速度；周宏喜等人[6]分析了立磨机内研磨介质的运动情况，讨论了研磨介质在不同磨矿区域产生的研磨效果；谢朋书等人[7]基于离散元方法分析了立式螺旋搅拌磨研磨介质尺寸分布、搅拌器转速以及导程对磨矿效果的影响，并提出了综合磨矿性能指标，为磨机优化设计提供了参考方法；李留政等人[8]采用离散单元法对立式螺旋搅拌磨的磨矿过程进行了分析，发现介质球速度与搅拌器转速及介质球径向方向上所处的位置关系较大，且介质球碰撞力、碰撞次数与搅拌器转速、介质球填充率有很大关系。

目前，立式螺旋搅拌磨使用的研磨介质多为高铬钢球，其以较低的价格在磨矿行业备受欢迎。钢球密度大，在研磨过程中会产生很大的能耗；普通的陶瓷球虽密度小，但硬度过低，并不适用于研磨作业[9]。随着耐磨材料技术的发展，近年来出现了一种以氧化铝为基本材料的新型纳米陶瓷球，相比于钢球，其具有更节能、更耐磨等优势，发展前景更广阔。

笔者采用 CFD-DEM 耦合的方法建立矿浆与研磨介质的流固耦合模型，探究在使用不同尺寸的陶瓷球和钢球时，立式螺旋搅拌磨的磨矿特性以及能量损耗，并结合立式螺旋搅拌试验磨机的试验结果，分析使用不同材料研磨介质时的磨矿特性，为立式螺旋搅拌磨研磨介质的选型提供依据。

1 数学模型

1.1 几何模型

立式螺旋搅拌试验磨机的结构非常复杂，在建立几何模型时要对其进行简化，只保留筒体和搅拌器两部分，由于其属于旋转器件，需要将流体域划分成静止域和旋转域两部分。立式螺旋搅拌试验磨机的几何模型如图1 所示，部分结构参数如表1 所列。

表1 立式螺旋搅拌试验磨机结构参数Tab.1 Structural parameters of vertical spiral stirring test mill mm

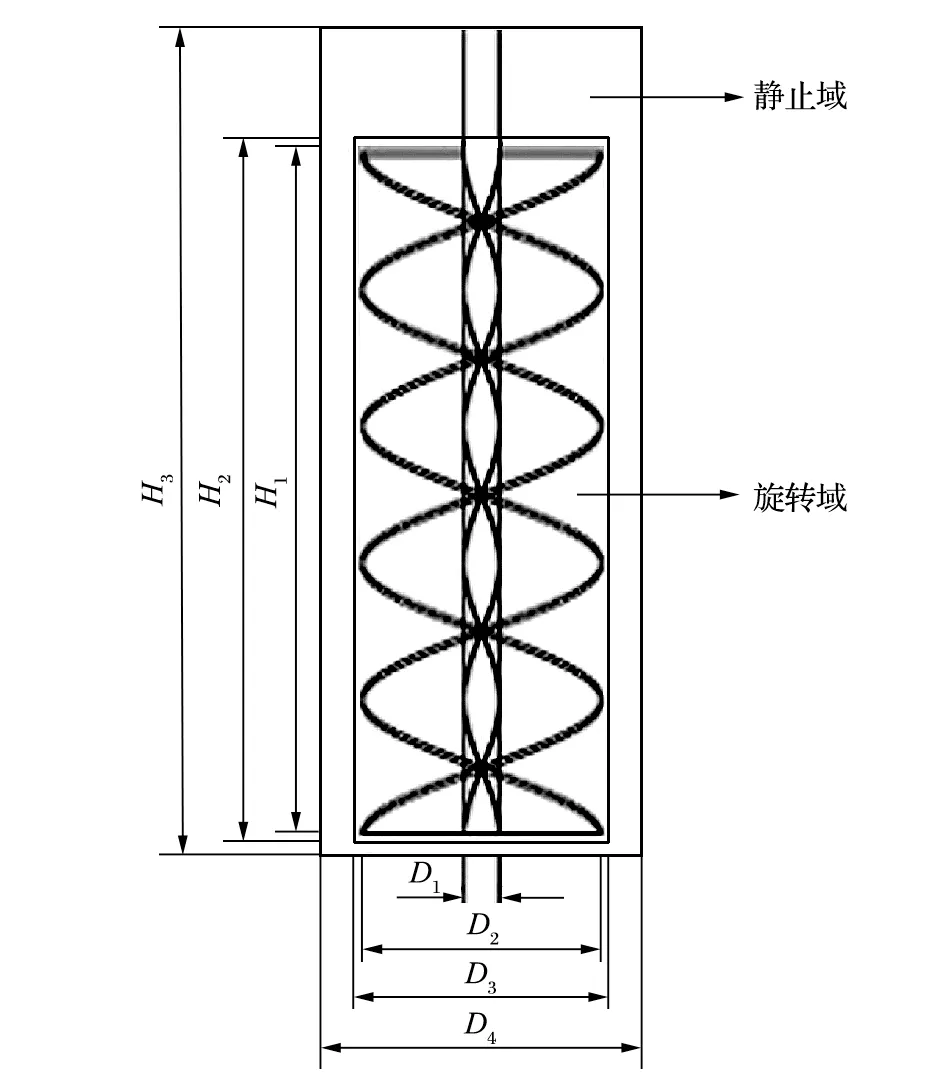
图1 立式螺旋搅拌试验磨机几何模型Fig.1 Geometric model of vertical spiral stirring test mill

在实际工况下，立式螺旋搅拌磨内部物质主要由研磨介质、矿石、水和空气组成，但矿石的入料粒度和研磨介质的直径相差较为悬殊，在仿真中很难准确模拟出矿石的破碎。因此，仿真中将矿石和水组成的矿浆视为单一的流体相[10]，且欧拉耦合模型只能应用于两相流，故该仿真忽略空气，默认磨机内部充满矿浆[11]。

1.2 固液两相流模型

物料和水组成的单一流体为矿浆，其密度和动力黏度[12]计算公式为

式中：C为矿浆质量分数；ρl为矿浆密度，kg/m3；ρw为水的密度，kg/m3；ρm为干矿密度，kg/m3；μl为矿浆动力黏度，Pa·s；μw为水的动力黏度，Pa·s；φl为矿浆体积分数，%。

矿浆处于恒温恒压下，且考虑到矿浆与研磨介质的相互影响，在守恒方程中加入一个额外的体积分数项[13]。由 Navier-Stokes 方程可知，矿浆的质量和动量守恒方程为

式中：εl为空隙率；t为时间，s；ul为矿浆流速，m/s；gl为矿浆重力加速度，m/s2；S为动量汇；n为筒体内研磨介质的数量；FD为研磨介质所受矿浆作用力的总和，N；V为筒体的体积，m3。

研磨介质的运动通过离散单元法 (DEM) 进行求解，离散元软件 EDEM 采用的是软球模型，允许两个刚体接触时有略微重叠，接触模型选择 Hertz-Mindlin(no-slip) 模型。颗粒所受的接触力可分为两个分量，即法向接触力和切向接触力，其求解方程分别为

式中，Fn为法向接触力，N；E*为等效弹性模量，Pa；R*为等效半径，m；δn为法向重叠量，m；Ft为切向接触力，N；G*等效剪切模量，Pa；δt为切向重叠量，m。

1.3 网格划分及边界条件

通常在欧拉耦合接口中，Fluent 流体域的网格尺寸要大于颗粒直径至少 3 倍，网格体积大于颗粒体积至少 10 倍。仿真中，由于研磨介质直径较大，满足此要求所划分的网格质量极差，需要修改耦合接口中关于体积分数的算法，以便能够满足网格无关性的要求。采用修改算法后的接口进行仿真验证，考虑计算准确性及运算效率，选取网格最小尺寸为 5 mm，最大尺寸为 15 mm 进行网格划分。由于磨机内部的研磨作用只发生在研磨介质与矿浆接触的部分，为了减小仿真与实际的差别，根据研磨介质在磨矿过程中能达到的最大高度，对磨机的几何模型进行截取。截取后的立式螺旋搅拌试验磨机网格如图2 所示，网格数量为 5.11 万个，最差质量为 0.4。

图2 立式螺旋搅拌试验磨机网格Fig.2 Grid of vertical spiral stirring test mill

搅拌器在旋转过程中会产生漩涡，为了提高计算涡流的精度，Fluent 中湍流模型选择 RNGκ-ε模型，选用标准壁面函数，出口设置为压力出口，时间步长为 EDEM 的 100 倍。由于要考虑研磨介质体积分数的影响，曳力模型选择 Wen Yu &Ergun 模型[14]。耦合接口连接前，在 EDEM 中对研磨介质进行预填充，预填充时搅拌器不转动。由于 Fluent 在仿真开始时引入颗粒会对内流场湍流引起较大变化，极易引起仿真发散，因此，须将体积分数项松弛因子调小后再初始化，待内流场稳定后再逐渐调大。磨机运行参数设置如表2 所列。

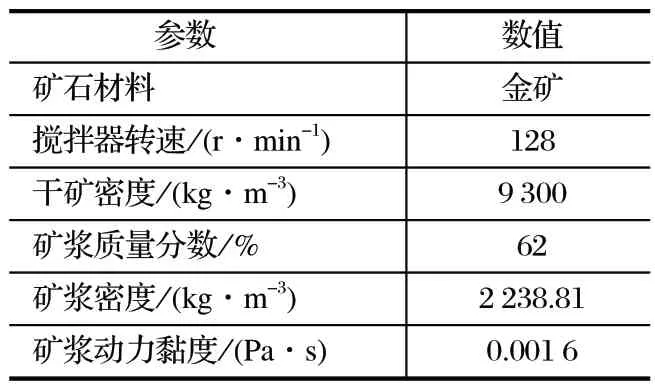
表2 磨机运行参数设置Tab.2 Mill operating parameter setting

首先进行φ8 mm 钢球介质磨矿仿真，然后利用φ8 mm 陶瓷球进行磨矿仿真，考察钢球和陶瓷球磨矿特性的差异。陶瓷球与钢球材料属性对比如表3 所列。由于陶瓷球密度比钢球小得多，因此进行以下 2种条件的陶瓷球磨矿仿真与试验。

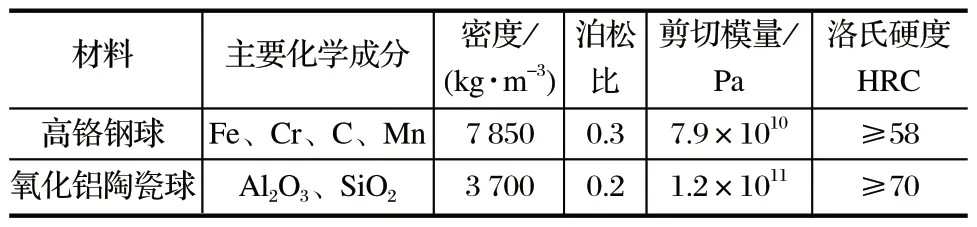
表3 研磨介质材料属性Tab.3 Material properties of grinding mediums

(1) 填充率相同，钢球为 150.0 kg，陶瓷球为 72.6 kg；

(2) 陶瓷球填充率大于钢球，陶瓷球为 100.0 kg。

2 结果分析与讨论

立式螺旋搅拌磨运行开始后，介质球和矿物会随着螺旋搅拌器的转动向上运动，当到达自由面时，又会在搅拌器与筒壁之间的环形区域内向下运动，如此往复，通过介质球之间、介质球与搅拌器和筒壁之间的剪切、摩擦以及冲击作用进行研磨破碎。Fluent 中介质球分布如图3 所示。

图3 介质球分布云图Fig.3 Distribution contour of medium balls

2.1 磨矿特性对比分析

由于仿真中将矿浆简化成一种单一流体，无法检测其出料粒度，因此，仿真的磨矿效果可以通过分析研磨介质的运动速度、碰撞次数以及碰撞力来间接评价。

2.1.1 运动速度

在距磨机底部 1/3 高处截取一平面，以搅拌器中心为原点，提取平面内距原点不同径向距离处的研磨介质平均运动速度，结果如图4 所示。

图4 研磨介质运动速度对比Fig.4 Comparison of motion velocities of grinding mediums

由图4 可以看出，随着距原点径向距离的增加，研磨介质的运动速度也逐渐增加，于搅拌器边缘处达到最大值；在搅拌器边缘距筒壁的环形区域内，研磨介质不被搅拌器的旋转所带动，其运动速度随着径向距离的增加而减小；同时，由于钢球质量较大，运动速度从始至终都要小于陶瓷球；在增加填充率后，陶瓷球作自上而下往复运动的距离增加，其在该平面内的速度也会有所增加。

2.1.2 碰撞次数

3 种研磨介质颗粒的碰撞次数对比如图5 所示。

图5 研磨介质碰撞次数对比Fig.5 Comparison of collision times of grinding mediums

从图5 可以看出，陶瓷球的碰撞次数远远大于钢球，这与研磨介质的运动速度有很大关系，速度越大，颗粒之间的碰撞次数越多。

2.1.3 碰撞力

提取 3 种研磨介质颗粒的法向碰撞力和切向碰撞力，结果如图6 所示。

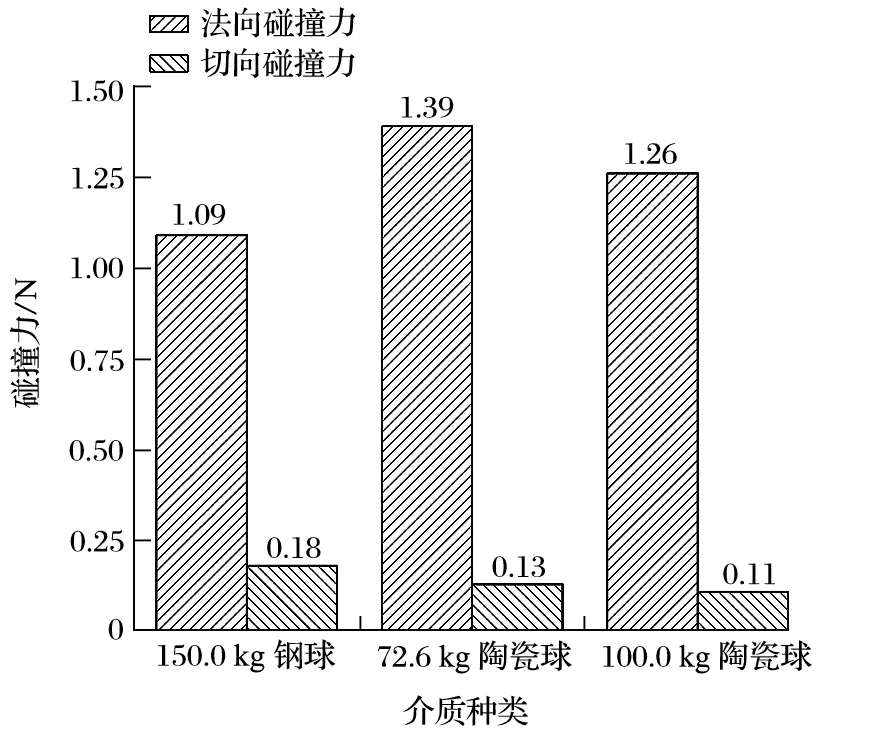
图6 研磨介质碰撞力对比Fig.6 Comparison of collision forces of grinding mediums

从图6 可以看出，相同填充率情况下，钢球法向碰撞力比陶瓷球小，切向碰撞力比陶瓷球大，但相比较而言，两种研磨介质的法向碰撞力差距比切向碰撞力差距大得多。在研磨过程中，法向碰撞力占主导作用，因此法向碰撞力更大的陶瓷球磨矿效果会更好。当提高陶瓷球的填充率时，法向碰撞力和切向碰撞力都有所下降，因此填充率并不是越大越好。

2.2 磨矿能耗对比分析

在磨机启动阶段，螺旋搅拌器要带动研磨介质和矿物由静止状态动起来，该阶段螺旋搅拌器会受到较大的静摩擦力和惯性力矩，此时转矩会急剧增大，随后逐渐趋于稳定。使用 3 种研磨介质进行仿真，提取的搅拌器转矩及平均值如图7～9 所示。

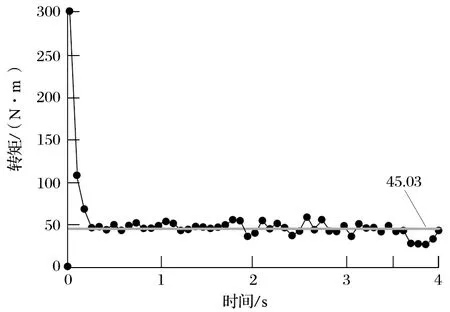
图7 使用 150.0 kg 钢球时的搅拌器转矩Fig.7 Stirrer torque with 150.0 kg steel balls

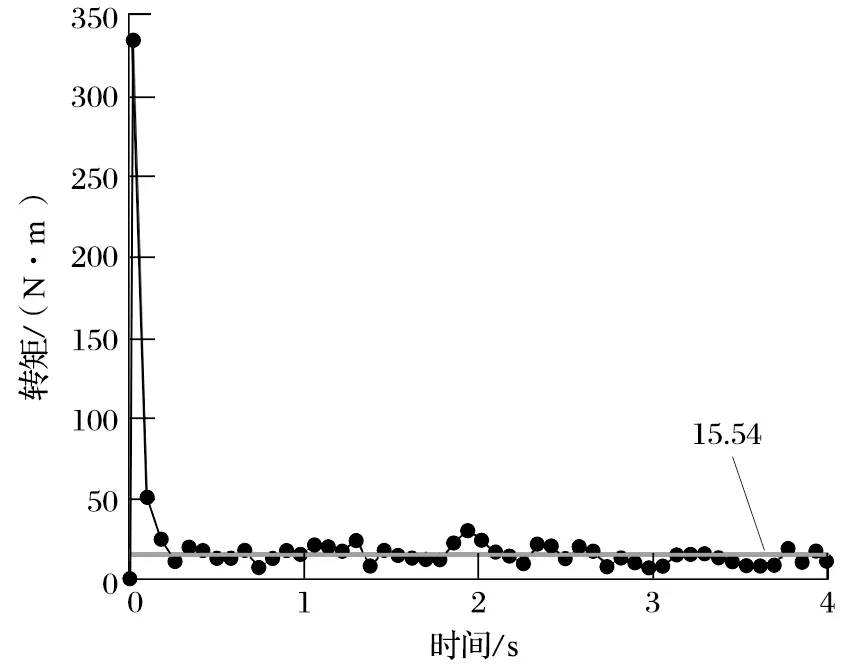
图8 使用 72.6 kg 陶瓷球时的搅拌器转矩Fig.8 Stirrer torque with 72.6 kg ceramic balls

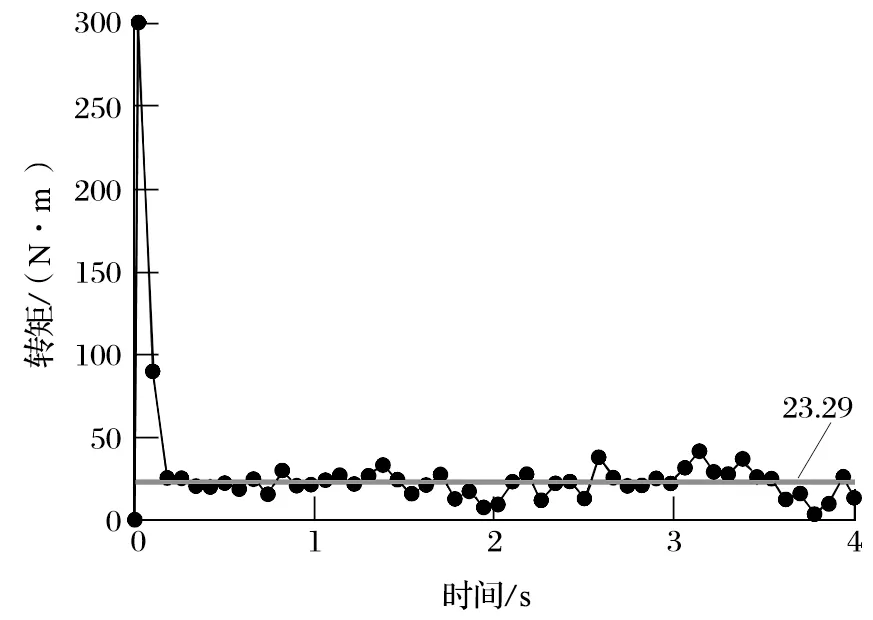
图9 使用 100.0 kg 陶瓷球时的搅拌器转矩Fig.9 Stirrer torque with 100.0 kg ceramic balls

能耗是衡量立式螺旋搅拌磨节能降耗的重要指标，搅拌器转矩、转速和磨矿时间的乘积即为立式螺旋搅拌磨在某时刻的能耗。在转速和磨矿时间恒定的情况下，转矩成为决定搅拌器能耗的重要因素。由图7～9 可知，由于陶瓷球的质量比钢球小很多，在相同填充率的情况下，使用陶瓷球作为研磨介质所产生的转矩要比使用钢球小得多；当填充率提高时，搅拌器的转矩也会随之提高，但与使用钢球所产生的转矩仍存在较大的差值。

2.3 试验结果对比分析

在立式螺旋搅拌试验磨机上，以金矿为物料，分别加入φ8 mm 钢球 150.0 kg、φ8 mm 陶瓷球 72.6 kg及φ8 mm 陶瓷球 100.0 kg 进行试验，试验参数与仿真参数保持一致，使用 KTR 转矩转速传感器检测搅拌器的转矩。分次进行磨矿溢流取样，记录每次取样时的搅拌器转矩，并计算磨矿吨功耗 (能耗/物料干重质量)，最后对溢流取样样品烘干，并进行 38 μm 和 45 μm 下粒度筛分分析。3 组试验测得的搅拌器平均转矩和物料处理量如表4 所列。

表4 试验测得平均转矩及处理量Tab.4 The average torque and throughput measured by test

由表4 可知，转矩与仿真所提取的基本吻合，误差在 15% 左右。不同磨矿条件下，磨矿吨功耗与磨矿产品细度的变化关系对比曲线如图10、11 所示。

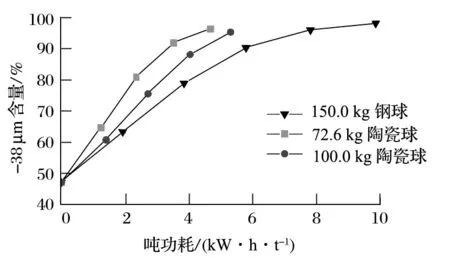
图10 吨功耗与 38 μm 粒度筛下含量对比曲线Fig.10 Comparison curve of power consumption per ton and content under sieve of 38 μm particle size

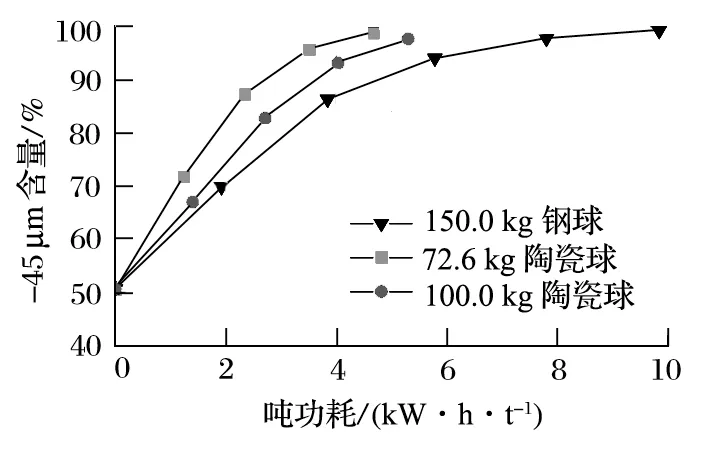
图11 吨功耗与 45 μm 粒度筛下含量对比曲线Fig.11 Comparison curve of power consumption per ton and content under sieve of 45 μm particle size

由图10、11 可知，根据磨矿试验结果，使用陶瓷球作为研磨介质时，立式螺旋搅拌磨达到出料粒度标准所需的时间虽然较长，但总功耗比使用钢球少得多。这是由于陶瓷球介质的总质量要比钢球介质小，螺旋搅拌器带动其进行运动所产生的转矩小，立式搅拌磨拖动功率也会相应减少。陶瓷球表面硬度高，耐磨性强，单颗粒介质与物料接触时在微观上产生的挤压磨削能力较钢球强，而钢球的耐磨性较差，磨损后呈不规则形状，会对搅拌磨衬板造成较大的损伤，并且在研磨过程中，陶瓷球消耗量比钢球少很多，具有一定的经济价值。在相同的填充率条件下，陶瓷球磨矿吨功耗确实低于钢球，但同时其磨矿处理量低于钢球。适当提高陶瓷球的填充率时，磨矿吨功耗增加，但处理量会有所提高。