基于响应曲面法的采煤机截割部扭矩轴优化设计

李小朋

1太重煤机有限公司 山西太原 030032

2智能采矿装备技术全国重点实验室 山西太原 030032

随着我国煤炭产业的发展，煤炭开采技术不断提高，最先进的电牵引采煤机截割功率不断增大，采煤机的性能参数不断地提高。在设计采煤机的时候，采煤机的可靠性是非常重要的一个考虑因素。扭矩轴是采煤机截割部一个重要的元件，用以保护截割部的传动系统。此外，扭矩轴还具有平稳地传递转矩、缓冲减震的作用[1]。在传统的采煤机扭矩轴设计中，通常会考虑它的结构形式、材料的选择以及加工工艺等因素，这些因素都会关系到扭矩轴的性能[2]。采煤机截割部扭矩轴的性能，直接影响采煤机的生产效率及工作的可靠性。在采煤机工作过程中，当电动机发生过载时，如果扭矩轴应当断裂而没有断裂，就会发生故障，电动机的寿命也会受到影响，甚至会发生更为严重的事故。如果采煤机正常工作时扭矩轴也经常发生断裂，即扭矩轴在设计时，其安全系数设计不合理[3]，扭矩轴损坏频繁需要进行更换，这将大大影响工作的效率。因此，有必要对采煤机扭矩轴进行深入研究。

1 基于有限元的扭矩轴分析

1.1 采煤机截割部扭矩轴模型的建立

采煤机截割部扭矩轴包括中心轴、卸荷槽以及外花键，其中卸荷槽靠近一端的花键，该花键用于电动机转矩输入，内部孔与扭矩轴组合形成离合器。扭矩轴卸荷槽基于缺口效应，在电动机过载时产生集中应力，从而发生断裂[4]。

目前，扭矩轴卸荷槽主要分为 U、V、I 等 3 种槽型，如图1 所示。对这 3 种不同槽型的扭矩轴施加同一转矩时，3 种扭矩轴的最大应力都集中在卸荷槽底部，并且应力集中的效果都比较明显。用 ANSYS对 3 种不同槽型的扭矩轴进行有限元分析，得出在满足设计要求的情况下，施加相同载荷时，U 形槽扭矩轴的变形量最小。采煤机在工作过程中，发生过载时，扭矩轴正常断裂，且形变量最小时，保护作用最好，对所接触的其他零件造成的损伤最小，更换效率高，减少了对生产的影响。因此，笔者选择 U 形槽扭矩轴进行进一步分析[5]。

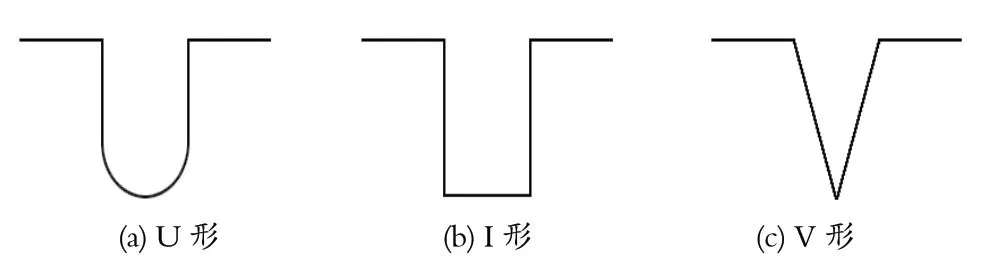
图1 不同结构形式的卸荷槽Fig.1 Load relieving grooves with different structures

采煤机截割部 U 形槽扭矩轴的结构如图2 所示。扭矩轴的结构参数有扭矩轴长度L，扭矩轴直径D，卸荷槽外径d、卸荷槽底端圆弧半径r和深度h，这些参数决定了扭矩轴的特征，其中深度h、底端半径r、表面状态、材质和疲劳强度决定扭矩轴的传递动力；扭矩轴长度L、直径D决定扭矩轴的扭转刚度；卸荷槽外径d、深度h、底端半径r、材质静强度标准决定其过载保护性能[6]。

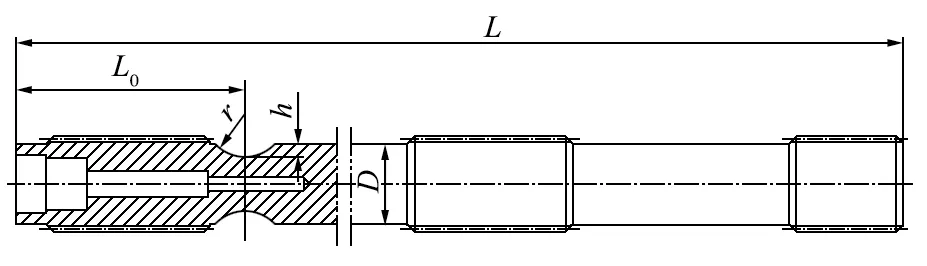
图2 扭矩轴结构示意Fig.2 Structure of torque shaft

根据扭矩轴结构形式，用 NX UG 进行三维建模，得到如图3 所示的扭矩轴三维模型。

图3 扭矩轴三维模型Fig.3 3D model of torque shaft

扭矩轴既要平稳可靠地传递转矩，又要在过载时及时保护电动机，所以其材料选择尤为关键。为满足实际生产需要，经过对比分析，扭矩轴材料最终选择采用 40Cr。40Cr 综合性能稳定，其性能如表1 所列，具有强度高、韧性强及热处理性能好等特点，在应用过程中通过淬透热处理可使其综合性能更加可靠。因此，采煤机截割部扭矩轴调质处理后能够达到使用要求[7]。

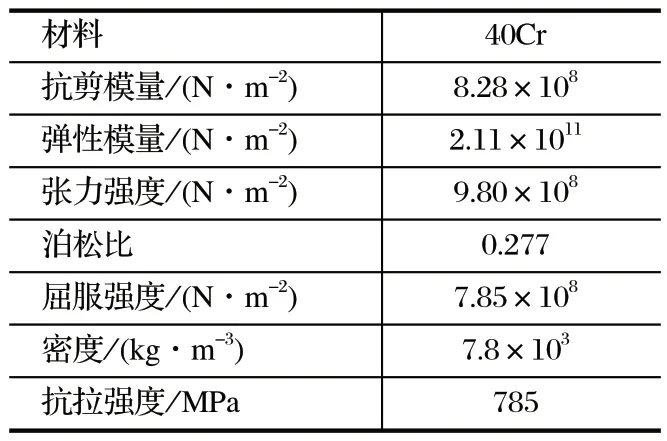
表1 40Cr 材料属性Tab.1 40Cr material properties

1.2 最大传递转矩的计算

根据最大切应力强度理论 (第三强度理论)，最大剪应力τmax达到了 0.5σb，材料发生断裂失效，扭矩轴的失效形式为断裂，故以抗拉强度极限σb进行校核[8]。

笔者选用的采煤机截割部电动机型号为 YBCS-200，额定功率为 200 kW，额定电压为 1 140 V。采掘过程中，要求采煤机截割部的三相异步电动机的扭矩轴在发生严重过载，即转矩倍数达到一定值时，扭矩轴可在 3～5 s 内断开，以保护电动机。扭矩轴是一根细长的传动轴，其卸荷槽是该轴上重要的设计环节，所以笔者只分析扭矩轴的卸荷槽位置即可。

所选扭矩轴为空心轴，当扭矩轴没有卸荷槽时，对其强度进行校核。

扭矩轴额定转矩

式中：P为电动机的额定功率，P=200 kW；n为电动机额定转速，n=1 578 r/min。

根据材料属性手册中推荐的 [τ]=(0.5～0.6)σb，σb=785 MPa，计算得 [τ]=392.5～471.0 MPa。

扭矩轴的最大承载转矩

式中：Mmax为扭矩轴卸荷槽的最大承载转矩，以电动机在 2.2 倍额定功率工作时输出的转矩为准，即Mmax=2Me。

将计算结果代入式τ=Mmax/Wp，计算得τ≤[τ]。没有卸荷槽的扭矩轴是安全的，但不能起到保护电动机的作用。因此需要在扭矩轴上增加卸荷槽，使得扭矩轴能够在一定载荷下断裂，从而保护电动机。

一般情况下，对电动机的过载保护是指超过电动机额定转矩的 2.5 倍。若过载扭矩不超过 2.5 倍，电动机就不会因瞬间转矩突然增大而烧坏。设计时，扭矩轴卸荷槽最大承载转矩定为电动机额定输出扭矩的2.2 倍，即当扭矩轴承受的转矩超过电动机额定转矩的 2.2 倍时，扭矩轴卸荷槽处将发生断裂[9]。在实际工况下，综采工作面采煤机截割部滚筒正常作业时会产生巨大的振动，当滚筒割煤时碰到岩石层或煤壁中存在夹矸现象时，滚筒的瞬间载荷会突然变大，导致扭矩轴被扭断，从而保护电动机不至被烧坏而影响整个系统[10]。

扭矩轴在载荷超限时应及时断裂。取材料抗扭强度最大值 471 MPa，即材料的最大应力超过其最大抗扭强度时，扭矩轴会被破坏。

对扭矩轴进行静力学分析的目的在于找出影响扭矩轴最大应力应变分布的规律，为扭矩轴的优化设计提供依据和基础。

2 不同结构参数下扭矩轴力学分析

对扭矩轴模型的相关参数进行修改，h取 8.5～10.0 mm，r取 31～25 mm，L0取 164～170 mm，用ANSYS 进行仿真，得到不同结构参数下扭矩轴的力学分析，并得到各个参数对应力、应变的影响曲线。

卸荷槽深度h对扭矩轴应力与应变的影响如图4所示，当扭矩轴卸荷槽的底端半径r和轴向位置L0不变时，随着卸荷槽深度h的增加，理论应力集中系数也随之增大，从而导致扭矩轴 U 形槽尖端的最大应力与应变也逐渐增大，最大应力主要集中在卸荷槽处，卸荷槽最低端的应力最大。

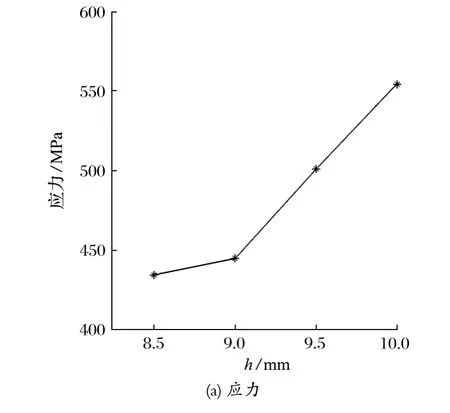
图4 卸荷槽深度 h 对扭矩轴应力与应变的影响Fig.4 Influence of depth h of load reliving groove on stress and strain of torque shaft

卸荷槽底端半径r对扭矩轴应力与应变的影响如图5 所示。当扭矩轴卸荷槽的深度h和轴向位置L0不变时，卸荷槽轴颈处的最大应力随着r的增大而减小。r的增加使得卸荷槽缺口趋于平缓，应力集中的效果变弱。应变的变化趋势基本与应力一样，并且应力与应变集中区域基本重合。

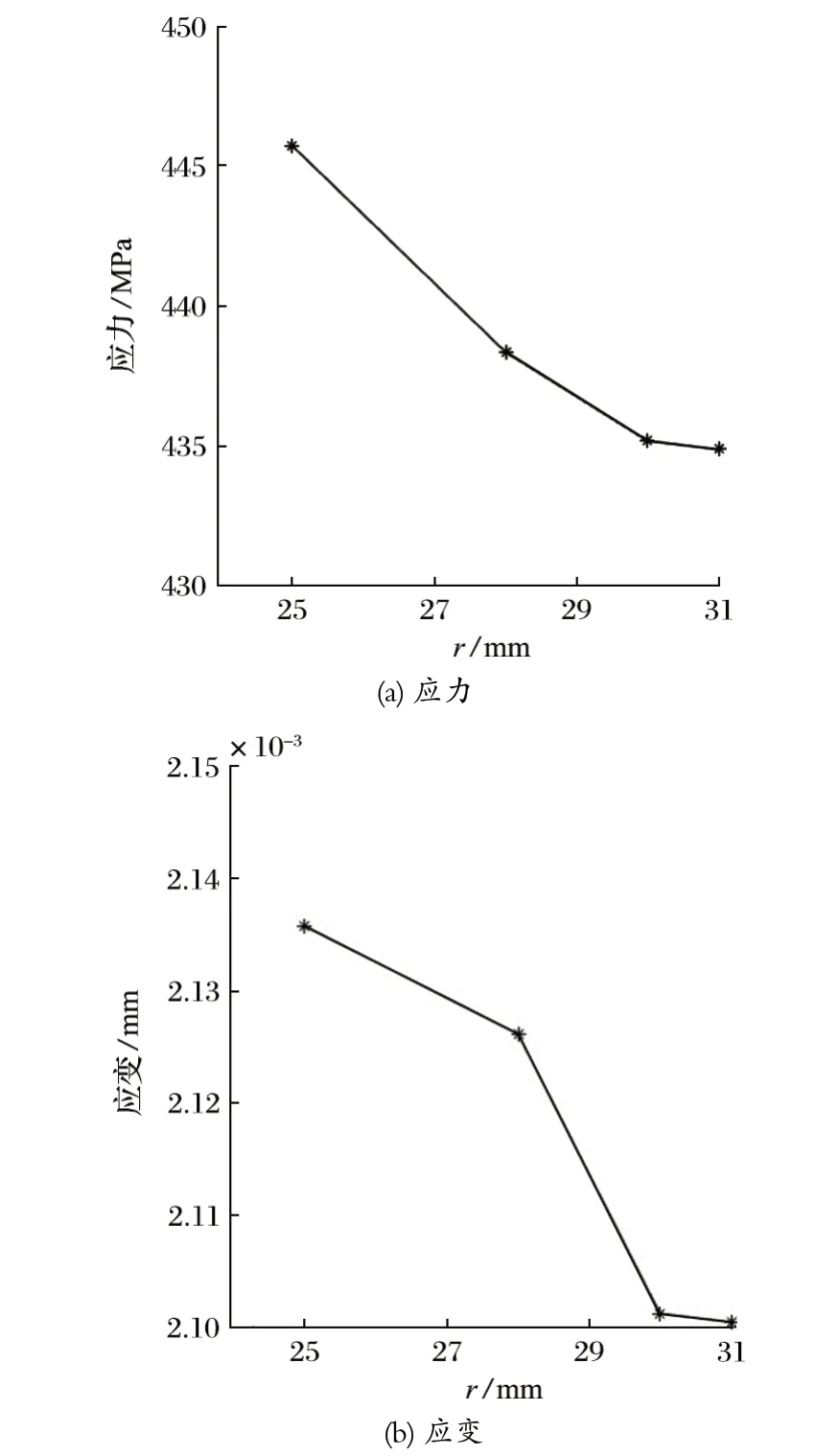
图5 卸荷槽的底端半径 r 对扭矩轴应力与应变的影响Fig.5 Influence of bottom radius r of load reliving groove on stress and strain of torque shaft

卸荷槽轴向距离L0对扭矩轴应力与应变的影响如图6 所示。当卸荷槽的深度h和底端半径r不变时，随着卸荷槽轴向位置L0的增大，最大应力先增大再减小。应变的变化与应力一致。

图6 轴向距离 L0 对扭矩轴应力与应变的影响Fig.6 Influence of axial distance L0 on stress and strain of torque shaft

3 响应曲面法试验设置

3.1 模型建立及试验

响应曲面设计方法是通过对响应输出变量到底如何依赖于自变量 (即影响因素) 进行研究分析，进而发现该如何设置不同的自变量，可以让输出响应达到最优点的附近区域，从而获得响应理想目标值[11]。

响应曲面法通过全因子试验设计、部分因子试验设计、中心复合设计及 Box-Behnken 设计等方法在实际工作中对过程进行试验，从而获取所需的相关数据，并根据回归设计、方差分析及最速上升等方法对所构建的数学模型进行拟合和优化设计[12]。

根据响应曲面法，利用初步试验来进一步确定影响扭矩轴的因素。笔者设置的因变量因子有 3 个：深度h，半径r，轴向距离L0。以 +1，-1 分别代表变量的水平，结果如表2 所列。通过表2 数据，进行 17个点的响应曲面分析试验，具体试验设计方案及结果如表3 所列。

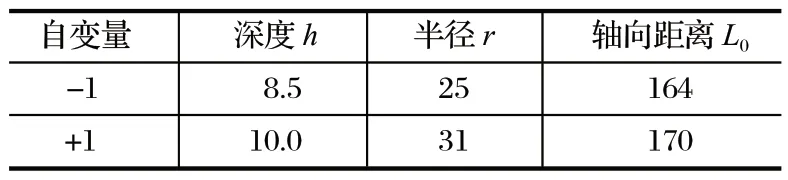
表2 响应曲面法分析因素和水平Tab.2 Analysis factors and levels by response surface method mm

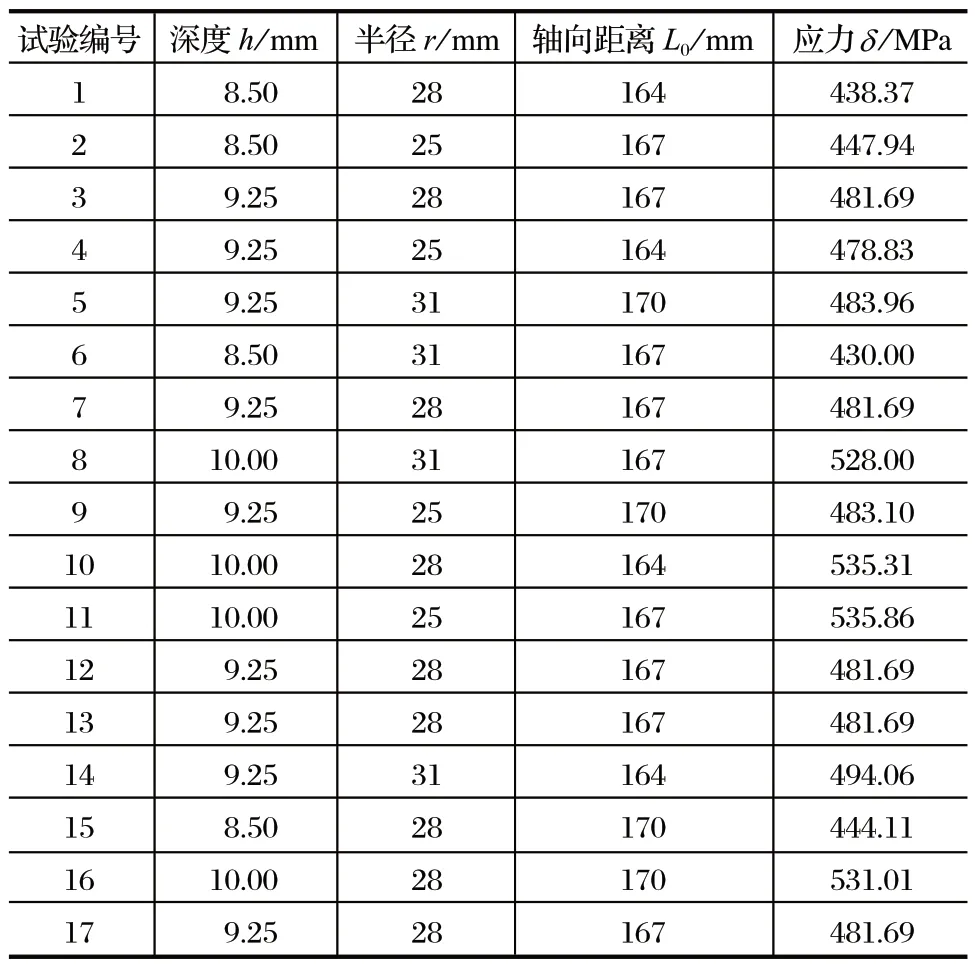
表3 响应曲面分析试验设计及结果Tab.3 Experimental design and results of response surface analysis

由表1、2 得到 Box-Behnken 的图像分析，如图7 所示。

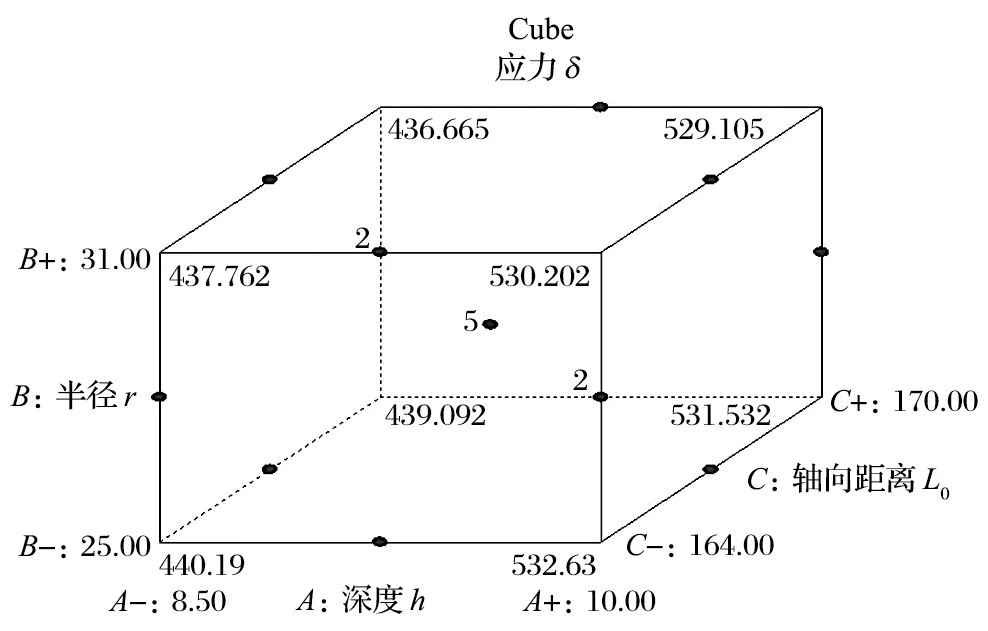
图7 Box-Behnken 图像分析Fig.7 Box-Behnken image analysis

利用 Design Expert 软件对数据进行二次多元回归拟合，得到应力δ与深度h、半径r、轴向距离L0之间的二次多元回归模型：

对该模型进行方差分析，结果如表4 所列。

表4 响应曲面回归模型的方差分析Tab.4 Variance analysis of regression model for response surface

3.2 响应曲面分析

利用 Design Expert 软件对表中数据进行二次多元回归拟合，所得到的二次回归方程的等高线及响应曲面如图8～10 所示。根据二次模型所得到的等高线及响应曲面可以评价试验因素之间的交互作用强度，以及确定各因素的最佳水平范围。

图8 深度 h 和半径 r 对应力 δ 影响的曲面和剖面图Fig.8 Surface and section views of influence of depth h and radius r on stress δ

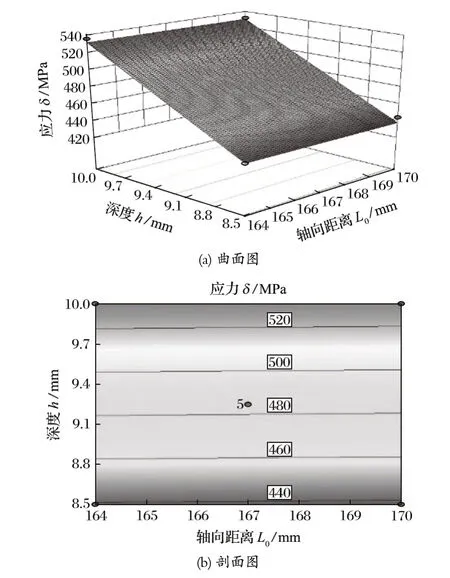
图9 深度 h 和轴向距离 L0 对应力 δ 影响的曲面图和剖面图Fig.9 Surface and section views of influence of depth h and axial distance L0 on stress δ

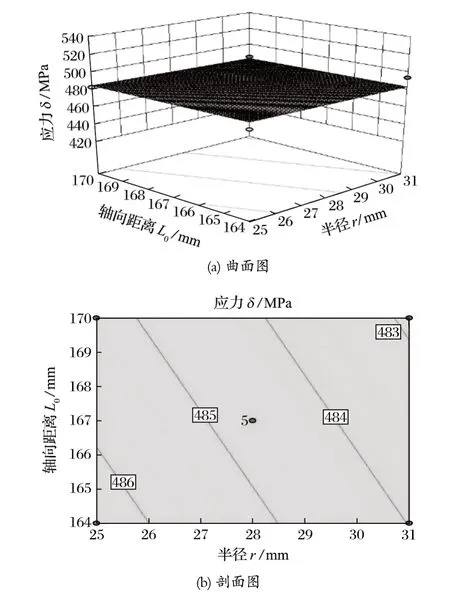
图10 半径 r 和轴向距离 L0 对应力 δ 影响的曲面图和剖面图Fig.10 Surface and section views of influence of radius r and axial distance L0 on stress δ

根据响应曲面分析得到最优的组合，当深度h=9.02 mm，半径r=27.62 mm，轴向距离L0=168.84 mm 时，得到应力为 471.001 MPa。

4 分析验证

根据扭矩轴卸荷槽参数，用得到的最优组合参数重新创建扭矩轴的三维模型，并用 ANSYS 做有限元分析，得到扭矩轴应力及应变云图，如图11 所示。

图11 重新设计后扭矩轴应力与应变云图Fig.11 Stress and strain contours of redesigned torque shaft

重新设计的扭矩轴应力为 470.75 MPa，Design Expert 软件分析得出的最优数据为 471.001 MPa。所得结构数值与响应曲面法所得结果的数值相差 0.053 3%，验证了响应曲面法分析数据的可靠性。

选取前文仿真试验最优结果h=9.25 mm，r=25 mm，L0=164 mm 的组合，以及通过响应曲面法得到的最优参数组合h=9.02 mm，r=27.62 mm，L0=168.84 mm，将以上 2 组参数制成扭矩轴，并在相同作用力情况下进行扭转试验。试验结果表明通过响应曲面法得到的最优参数组合结果较优。

5 结论

通过对截割部扭矩轴的工作状态和功能的分析，选择 U 形卸荷槽深度h、半径r、轴向距离L03 个参数作为优化参数。针对扭矩轴的实际受力情况，用NX UG 对扭矩轴进行三维模型的创建，通过 ANSYS进行了有限元仿真。用 Design Expert 对扭矩轴的 3 个参数进行修改，得出不同的扭矩轴应力的数值，并用响应曲面法对有限元分析结果数据进行分析，得出不同组合对应力影响的曲面图和剖面图，根据响应曲面分析得到最优的组合，当h=9.02 mm，r=27.62 mm，L0=168.84 mm 时，满足使用要求。用该组数据重新建模，并进行有限元分析，得到重新设计后的扭矩轴应力应变云图。由分析结果可知，该扭矩轴符合使用要求。进一步的试验对比，佐证了优化后扭矩轴参数的优异性，为扭矩轴的优化设计提供了理论指导，对提升采煤机整体的生产效益具有重要的意义。