基于统计和自适应ParNet的产学研绩效评价

张 睿，宋思琪，胡 静，张永梅，柴艳峰

（1.太原科技大学 计算机科学与技术学院，太原 030024；2.北方工业大学 信息学院，北京 100144）

0 引言

教育部办公厅于2020 年印发的《教育部产学合作协同育人项目管理办法》中明确指出，“积极支持第三方机构开展项目评价，健全统计评价体系。强化监测评价结果运用，作为试点开展、激励约束的重要依据”［1］。可见，构建完整、科学的绩效智能评价体系和方法、开展科学合理的产学研绩效智能化评价非常必要。在评价体系方面，Wang［2］围绕产学研合作中有关知识共享的特征、目标和影响因素，设计出绩效评价指标体系；常洁等［3］基于资源、知识、技术、风险四个协同要素提出的假设，总结了影响中小科技企业协同创新绩效的因素；周广亮等［4］以我国不同地区的30 个省份为研究对象，构建出分为科技成果产出和科技成果转化两阶段的创新绩效评价体系。综上所述，现有产学研绩效评价体系仍存在评价主体及评价角度单一、指标涵盖范围不够全面的问题。在评价方法方面，由于评价样本属于非线性的一维离散序列，传统的机器学习方法很难充分挖掘样本非线性特征及指标间的关联性特征，导致评价效果难以保障。

随着深度学习技术的发展，深度分类模型为离散序列的分类决策提供了新的技术支持和新视野［5］。近年来，许多学者将深层神经网络与绩效评价进行了有效的组合创新，并利用神经网络模型验证评价系统的有效性，如：Li［6］以现有创业网络研究为基础，分析新公司之间的网络关系，提出基于自组织映射神经网络算法的社会创业能力和新公司绩效，进而建立创业网络和新的业务绩效模型；Shen［7］以跨境电子商务国际贸易绩效为研究对象，开发基于深度神经网络的跨境国际贸易绩效分类模型。通过分析上述研究，现阶段基于评价指标的深度学习分类方法主要通过离散序列各点直连的方式构成一维连续序列，然后直接输入深度分类模型中进行决策，这类方法存在很多局限性：1）一维序列所能表达的特征有限；2）深度卷积模型更贴合对高维样本的特征提取，虽也有一维卷积神经网络，但已被证实效果不如二维卷积神经网络。因此，如何充分挖掘离散评价样本特征的同时科学提高评价模型的准确率仍需进一步研究。

此外，深度分类模型中包含学习率、迭代次数、网络层数等在内的超参数多依赖人工主观性设定，通常存在模型冗余度较高且自适应能力弱的问题。针对这些问题，很多学者进一步探索基于智能优化算法的模型自优化策略，以提高模型自适应性，同时降低研究和时间成本。Yang 等［8］提出了基于集体引导因子［9］的探路者算法，以改善霍普菲尔德神经网络的结构；Sadeghi 等［10］提出了一种新的多目标二元黑猩猩优化算法和深度卷积神经网络的混合方法，以实现最优特征选择，并利用所提方法对极化合成孔径雷达（POLarimetric Synthetic Aperture Radar，POLSAR）图像进行分类；Naveena等［11］设计了一种融合飞蛾火焰优化（Moth-Flame Optimization，MFO）算法和乌鸦搜索算法（Crow Search Algorithm，CSA）的新型算法，并结合卷积神经网络进行最优特征选择，提出的模型可以有效提高血糖水平预测性能；梁军等［12］提出了一种基于改进粒子群优化算法和遗传变异的图像分割模型，首先对粒子群优化算法进行改进，增加了随机邻居粒子位置对自身位置的影响，扩大了算法的搜索空间；其次结合遗传算法的变异操作来提高模型的泛化能力。刘威等［13］提出融合混沌优化、振幅随机补偿和步长演变机制改进的原子搜索优化（Improved Atom Search Optimization，IASO）算法，优化了BP 神经网络（Back Propagation Neural Network）参数，成功应用于任务分类。上述模型优化策略均在实际应用中取得成效，但仍然存在一些不足，如：1）种群初始化时，个体分布不够广泛、均匀，不利于算法收敛；且普通个体携带有效信息较少，其他个体若盲目向当前个体学习则会导致算法难以快速搜索到最优解；2）算法迭代至后期，容易陷入局部最优，进而影响算法的寻优效果；3）现有算法的研究多集中在对浅层低维（2～3 个）超参数模型的优化设计，并不适用于含有高维超参数的深度卷积模型的快速自适应寻优。

针对上述问题，本文开展了基于统计和自适应ParNet（Adaptive Parallel Network，AParNet）的产学研绩效评价研究，主要工作如下：

1）设计包括产学研合作中学校、企业与学生三方合作主体的贡献、相关研究成果产出及各方对于其他合作主体的主观评价等关键要素在内的产学研绩效评价指标，并通过主客观综合赋权求出各指标权重，最终构建产学研绩效三级评价体系，为绩效评价提供充足的数据保障。

2）为丰富产学研绩效评价中离散样本自身的特征表达，将量化后的离散数据通过映射到极坐标空间、马尔可夫转移矩阵等不同高维空间域，转化为不同的二维空间域映射数据集，以提高离散数据特征挖掘的丰富度。

3）为进一步实现深度分类模型轻量化压缩及高维超参数的自适应优化，提出一种基于精英反向翻筋斗觅食的混沌算术优化算法，以丰富种群多样性、提高算法寻优效率，最终面向评价应用实现AParNet模型高效全局压缩与超参数优化。

1 产学研合作绩效评价体系构建

科学合理的评价体系是实现精准智能评价的前提保证，因此构建评价体系为后期的评价算法提供有效的数据依据。分析现有研究发现，在产学研合作绩效评价体系中，对于评价指标赋权方法的研究大多集中于层次分析法、熵权法、专家经验判定法等主观赋权方法，评价指标的赋权相对主观，影响最终评价效果。为解决这一问题，本文构建一个主客观综合赋权的产学研绩效评价体系，大致流程是：先设置三级评价指标，再对各指标进行主、客观综合赋权，最后以模糊数学理论为基础，对评价结果进行量化［14］，得出适用于产学研绩效智能评价模型的数据集。构建产学研合作绩效评价体系流程如图1 所示。

1.1 评价指标的设计及综合赋权

以往的产学研绩效评价指标主要存在指标覆盖范围较小、指标不够细化、评价主体单一等问题，本文通过对产学研合作过程各环节中绩效产出影响因素的深入分析，筛选归纳出不同评价主体、评价方法在“输入-过程-输出-发展”各关键环节中信息、资源、规则等要素。主要围绕参与产学研合作的校方、企业以及学生三方评价主体，具体将各方的贡献以及合作质量两方面作为一级评价指标，并基于此逐级细化出二级指标和三级指标，再基于模糊数学的数理统计方法，并结合主、客观综合赋权，进一步构建出高理论饱和度的产学研绩效评价体系，具体评价指标及权重可见4.2 节。

基于上述指标体系，对各指标进行主客观综合赋权，以进一步完成绩效评价，具体的权重计算分以下3 个步骤：

步骤1 优序图法［15］是将多个指标进行两两对比，最终按重要程度给出排序。该方法应用比较简单，且既能处理定性问题，又能处理定量问题，故本文采用优序图法求出每个评价指标的主观权重，具体请多位领域专家根据指标的相对重要性，对优序图上的指标进行两两对比打分，分数范围为1 到5 分，然后对优序图中的分数按行求和，并分别与优序图中的总分相除，得出各指标的主观权重ηj(j=1，2，…，n)。

步骤2 CRITIC（CRiteria Importance Through Intercriteria Correlation）权重法［16］是一种基于数据波动性的客观赋权法，它的思想在于通过对比强度和冲突性两项指标综合衡量评价指标的客观权重。为减少相关性较强的指标之间的信息重叠，本文利用CRITIC 法计算各评价指标的客观权重，具体计算步骤为：

1）收集产学研绩效评价体系中各评价指标对应的初始数据，组成原始指标数据矩阵，如式（1）所示：

其中：n为样本数，p代表评价指标。再由式（2）对矩阵中的数据做无量纲化处理：

式中：xij表示第i个样本中第j项指标的数值，xj、xmin和xmax分别代表对应第j项评价指标下，所有样本的数据之和、数据的最小值与最大值；

2）由式（3）～（5）依次计算各指标间的标准差Sj、相关系数Rj及信息量Cj：

其中：rij表示第i个样本中，j个评价指标之间的相关系数。

最终由式（6）计算出各评价指标的客观权重βj(j=1，2，…，n)。

步骤3 为缩小综合权重与主、客观权重间的离散程度，本文利用最小鉴别信息原理［17］对各指标主、客观权重进行综合处理。由拉格朗日乘数法计算得出各指标的主客观综合权重Wj(j=1，2，…，n)，见式（7）～（8）：

式中：minF为目标函数，βj和ηj分别表示指标的客观权重和主观权重。

1.2 评价结果量化

为提供后续产学研绩效智能评价的数据集，现以模糊数学理论为基础，对评价结果进行量化体现。步骤如下：

步骤1 根据设置的评价指标确定评价因素集，如U={u1，u2，…，un}，其中u1，u2，…，un可继续细化为二级指标和三级指标；再建立评语集V={优秀，良好，合格，不合格，异常}；将评价体系中最终求出的综合权重Wj作为权重向量P。

步骤2 评价指标包含定性与定量两种类型，分别使用模糊统计法和指派法计算它们的隶属度矩阵。

1）对定性指标：邀请学校、企业和学生三方评价主体共m名代表，按评语集中的评价等级对各主观指标进行评定，统计结果后，由式（9）计算得出各定性指标从因素集U对应到评语集V的模糊映射矩阵R'ij=(ri1，ri2，…，rie)。

2）对定量指标：本文根据指标特点选择极大型梯形分布隶属度函数［18］，如式（10）所示；再将各项指标得分归一化后得出评价标准参数：a1=0.14，a2=0.2，a3=0.25，a4=0.3，a5=0.35，a6=0.4，a7=0.5，a8=0.52；将实际值代入式（10）中求出指标隶属度αi，得到各定量指标从因素集U到评语集V的模糊映射矩阵R″ij=(ri1，ri2，…，ri(n-e))；联立定性与定量两类指标的模糊映射矩阵，构造综合的产学研绩效评价指标隶属度矩阵R。

步骤3 由式（11）计算得出模糊评价结果矩阵B'j；再进一步量化分析，本文先给评语集中各评价等级赋予分值，如｛优秀=90，良好=65，合格=55，不合格=50，异常=45｝，然后根据式（12）计算各评价样本的综合得分G。最终本文将综合得分在分数区间［65，90］内的数据设置为A 类、在［55，65）内的数据为B 类、在［50，55）内的数据为C 类、在［45，50）内的数据为D 类。

式中：b'j为评价样本隶属于各评价等级的程度；pi和rij分别表示各指标权重和指标隶属度，由它们分别组成指标综合权重向量P和指标隶属度矩阵R；gj代表对评语集中第j个评价等级所设定的分数。

2 产学研合作绩效评价方法

科学的评价方法是实现产学研绩效智能化评价的有力保障。因此，本文设计出基于AParNet 的产学研绩效智能评价方法，整体评价流程如图2 所示。

图2 基于AParNet的产学研绩效智能评价流程Fig.2 Flow of performance evaluation of industry-university-research cooperation based on AParNet

2.1 离散序列多空间域映射

由于量化后的产学研合作绩效样本是离散数据，包含的特征信息有限，为丰富评价样本的特征表达，本文对样本数据进行多空间域转换，通过构建马尔可夫转移矩阵及极坐标转换的方式，分别将一维离散数据映射至：马尔可夫转移场域（Markov Transition Field，MTF）［19］、格拉姆角差场域（Gramain Angular Difference Field，GADF）、格拉姆角和场域（Gramain Angular Summation Field，GASF）中，将得到的二维图像作为输入分类模型的数据集：一方面契合卷积神经网络对二维图像的特征提取优势，另一方面更丰富地表征出样本特征及评价指标间的关联性特征。

MTF 将序列数据映射到对应的值域区间后，基于一阶马尔可夫链，结合相邻样本间马尔可夫转移概率，构建出马尔可夫转移矩阵，如式（13）所示，进而拓展为马尔可夫转移场，实现图像编码，以充分挖掘序列数据的位置分布关系。

式中：x(t)表示一维离散序列，n为样本数，ωij为相邻样本间由区间qi到qj的转移概率。

格拉姆角场域（Gramain Angular Field，GAF）［20］将直角坐标系下的离散数据转化为极坐标表示，再通过计算各角度对应的三角函数值，生成GAF 矩阵，GAF 在使用两角差或两角和的三角函数时，分别会得到GADF 与GASF，式（14）、（15）为具体变换表达式。格拉姆角场域的优势在于能通过对不同点间角度和或角度差的处理方式来挖掘不同数据间的相关性。

2.2 基于精英反向翻筋斗觅食的混沌算术优化算法

为了更好地挖掘离散数据特征和特征之间的关联性，本文选择分类准确率较高且模型深度只有12 层的ParNet（Parallel Network）神经网络作为产学研绩效评价的基础网络。ParNet 模型［21］的优势在于采用并行结构，具有多尺度多分辨率的特征提取方式，有利于充分挖掘样本特征表征及特征间的关联性，可以进行快速、低延迟的推理。此外，相较于一些现有的轻量级网络，ParNet 更贴合产学研绩效评价的样本特点（具体验证见4.4 节）。

而深度分类模型在面向不同数据集时对模型结构的设计以及模型中包括学习速率、迭代次数、层数、每层神经元数和批大小等在内的超参数的设定，仍需依靠研究人员大量的主观经验进行决策，模型自适应能力较弱，且结构冗余度较高。针对这些问题，本文探索基于智能优化算法的模型自优化策略，对模型内部超参数进行自适应寻优，提高模型自适应性，降低研究和时间成本。

算术优化算法（Arithmetic Optimization Algorithm，AOA）是Abualigah 等［22］提出的一种根据四则运算思想设计出的元启发式算法。AOA 利用乘除运算进行全局搜索，使解的分布更加分散，增强算法的全局寻优能力；利用加减运算则有利于种群在局部范围内充分开发，加强算法的局部寻优能力。算法主要分为初始化阶段、探索阶段和开发阶段三个阶段。为更好地贴合对评价模型中多维超参数的自适应优化，本文在原AOA 的基础上，引入精英反向解的概念，同时融合多策略优化，提出一种基于精英反向翻筋斗觅食的混沌算术优化算法（improved Arithmetic Optimization Algorithm based on Elite opposition-based，EAOA）。

为快速实现对用于绩效评价的深度模型中的超参数的全局搜索，有效避免对模型超参数搜索过程中种群多样性随算法迭代而降低、影响搜索效率的问题，本文用Piecewise 混沌映射取代随机初始化种群。混沌映射［23］是生成混沌序列的一种方法，具有非周期、收敛快等优点。本文将4 种常见的混沌映射迭代105次后得到各自取值的分布曲线，如图3所示。从图3 中可以看出，Piecewise 映射、Logistic 映射、Cubic 映射与Gussian 映射均分布于［0，1］。其中，经 过Piecewise 混沌映射迭代后的取值分布更加均匀，它的表达式见式（16），再将混沌个体经式（17）转换到相应的搜索空间中。

图3 四种常见混沌映射的直方图分布曲线Fig.3 Histogram distribution curves of four common chaotic maps

式（16）中P为控制参数。式（17）中：Xub，d、Xlb，d分别是个体的上、下边界。

同时为避免对ParNet 中超参数进行自适应寻优时，个体盲目地向附近普通个体学习而忽视精英个体所携带的有效信息，导致算法陷入局部最优，从而影响搜索到最适合于ParNet 的超参数的概率，本文在AOA 搜索阶段加入了精英反向学习策略，思路是先求出当前可行解的反向解，从当前解及它的反向解中选取较优解作为下一代。具体步骤为选取普通个体对应的极值点作为携带更多有效信息的精英个体［24］，再根据式（18）求出精英个体的反向解，并在精英反向解及当前种群中选出优秀个体。

在AOA 中，数学优化器加速函数（Math Optimizer Accelerated，MOA）是协调算法全局与局部搜索的关键数学模型，表达式如式（20）所示。开始寻优前，在［0，1］内取随机数r1，若r1>MOA，算法进入探索阶段；否则进入开发阶段。

式中：max和min分别代表加速函数的最大值和最小值，n、NMax分别表示当前迭代次数和最大迭代次数。

算法进入探索阶段时，主要利用除法策略和乘法策略使算子进行全局搜索；算法进入开发阶段时，基于加法策略和减法策略使算子在搜索空间中个体较密集的区域中进行局部搜索。AOA 在搜索阶段与开发阶段上的位置更新公式如式（21）、（22）所示。其中，数学优化器概率（Math Optimizer Probability，MOP）的表达式如式（23）所示，式中敏感参数α取值为5。

为提高对ParNet 中超参数的全局搜索能力，避免算法迭代至后期，个体均聚集于当前最优个体周围，导致种群多样性迅速下降，从而降低搜索到模型最优超参数的概率，本文在开发阶段引入翻筋斗觅食策略，表达式如式（24）所示。翻筋斗觅食策略灵感来源于Zhao 等［25］受蝠鲼捕食方式启发提出的蝠鲼觅食优化算法。在此策略中，由当前位置出发，以最优解位置为中心点，个体在它的周围以翻筋斗的方式寻找新的位置。算术优化算法中个体翻筋斗示意图如图4 所示。

图4 算术优化算法中个体翻筋斗示意图Fig.4 Individual somersault diagram in arithmetic optimization algorithm

3 基于EAOA的ParNet模型自优化

利用改进后的EAOA 对ParNet 模型从全局及局部两方面展开自适应寻优，优化步骤如算法1 所示。全局方面，通过将模型中相邻且重复出现的相同模块个数作为决策变量，对模型做轻量化压缩，去掉其中冗余的结构模块，减少模型参数；局部方面，对模型内部的超参数做自寻优，进一步提高模型的自适应能力，从而有效降低研究和时间成本。本文具体以模型内部3 个并行的流结构中的注意力机制RepVGGSSE（RepVGG-Skip-Squeeze-and-Excitation）模块数为决策变量，对ParNet 进行轻量化压缩，同时对学习率、批量大小、激活函数、迭代次数和优化器这些超参数进行自寻优。测试训练好的模型效果时，由式（25）计算种群中个体i的适应度函数值［26］fit(i)，再根据fit(i)动态更新种群并选出最优个体，最终得到优化后的自适应分类模型AParNet。

式中：N代表迭代次数，t(i)和p(i)分别表示类别预测正确的样本数和类别预测错误的样本数。

算法1 EAOA 的伪代码。

输入 初始化算法参数α，η；

输出 网络架构的最佳值Ybest、最佳适应度值Fg。

4 实验与结果分析

4.1 实验平台

本文实验在Intel Core CPU I5-10400F、GIGABYTE RTX 3060 显卡、16 GB 内存、64 位Windows 操作系统、Matlab R2020b、PyCharm2021.3.3 中进行。本研究收集了2009—2019 年各省专业学位硕士招生数和在校生数、各学科专业的招生数以及人力资本积累等相关数据。其中，研究生就业数据来源于2009 — 2019 年《中国学位与研究生教育发展年度报告》系列书籍；人力资本积累相关数据来源于中央财经大学中国人力资本与劳动经济研究中心项目数据；其他数据根据教育部、国家统计局官方发布的2010—2020 年的《中国统计年鉴》《中国教育统计年鉴》中的数据计算所得。

4.2 构建评价体系与量化评价结果

针对目前产学研绩效评价指标涵盖面较为单一，且依据传统方法构建的评价体系，难免会带有主观性和片面性的问题，本文提出面向三方合作主体，基于模糊数学的数理统计方法并结合主客观综合赋权的产学研绩效三级评价体系，具体指标及权重如表1 所示。

表1 产学研绩效评价体系及指标权重Tab.1 Performance evaluation system and indicators for industry-university-research

4.3 数据预处理

量化处理后的评价结果仍是离散序列数据，其中收集到39 条A 类样本、44 条B 类样本、106 条C 类样本和11 条D 类样本，共计200 条样本。

为更充分地挖掘样本特征，本文对量化后的样本数据进行多域转换，将离散数据转换为连续序列形式，同时，将离散数据映射到MTF、GADF 和GASF 四种空间域中。多空间域转换对各类样本的特征增强效果如图5 所示。

图5 各类评价样本的多域处理效果Fig.5 Multi-domain processing effect of various evaluation samples

同时，为避免在训练过程中出现过拟合现象，本文通过调用Python 中的OpenCV 计算机视觉库，对映射到各空间域中所得到的二维图像做旋转、镜像及平移等数据增强操作，将各空间域数据集中的A、B、C、D 四类数据都扩充至680、960、1 280、880，共3 800，并按4∶1 划分成训练集和测试集。

4.4 多空间域特征表达及基础网络性能对比

为验证本文所选的基础网络ParNet 在产学研绩效智能评价领域的有效性，并选取出在产学研绩效评价中能够达到更好分类效果的高维空间域，对RegNet、ShuffleNetV1、ShuffleNetV2、EfficientNetV1、EfficientNetV2、ParNet 这6 种卷积神经网络的分类效果进行比较，记录在不同空间域下这6种网络的分类准确率，对比结果如表2 所示。

表2 多空间域在不同网络下分类准确率对比 单位：%Tab.2 Comparison of classification accuracy for multiple spatial domains under different networks unit：%

分析实验数据，首先对表格中的数据按列进行比较，ParNet 在四种空间域数据集上的分类准确率在不同的网络模型中总是最高的；此外，各模型在GASF 数据集上训练的分类准确率均高于其他空间域数据集上的准确率。说明在产学研绩效智能评价中，ParNet 与绩效评价的GASF 数据集间具有更好的契合度，能达到更好的分类效果。因此本文将ParNet 作为基础网络，同时在GASF 空间域中处理数据。

4.5 EAOA性能验证

为验证EAOA 的性能，本文在10 个标准测试函数上对海洋捕食者算法（Marine Predators Algorithm，MPA）［27］、鲸鱼优化算法（Whale Optimization Algorithm，WOA）［28］、麻雀搜索算法（Sparrow Search Algorithm，SSA）［29］、灰狼优化（Grey Wolf Optimizer，GWO）算法［30］和AOA 五种对比算法做仿真实验。这10 个标准测试函数包括：Sphere（F1）、SchwefelN2.22（F2）、SchwefelN1.2（F3）、SchwefelN2.21（F4）、Rosenborck（F5）、Step（F6）这6 个单峰测试函数，以及Schwefe（lF7）、Rastrigin（F8）、Ackley（F9）、Griewank（F10）这4个多峰测试函数。

统一设置算法参数如下：种群规模为500，维度为7，最大迭代次数为500。为避免寻优结果的偶然性，将各算法在10 个测试函数上独立运行30 次，选取30 次结果的平均值（Mean）和标准差（Std）作为算法最终评价指标，各算法的寻优结果如表3、4 所示，其中最优结果被加粗标出。

表3 单峰测试函数实验结果Tab.3 Experimental results of unimodal test functions

从表3 可以看出，EAOA 在6 个单峰测试函数上独立运行30 次，均能得到理想的目标函数值，且所求解的平均值与标准差都优于其他5 种对比算法。证明在单峰测试函数上，EAOA 寻优能力高于其他对比算法，稳定性也最好。

从表4 可以看出，与其他5 种智能优化算法相比，EAOA在求解4 个多峰测试函数时均能得到最优解，因此，EAOA 稳定性更高且在寻优过程中具有相对更强的全局性和收敛性。

表4 多峰测试函数实验结果Tab.4 Experimental results of multimodal test functions

4.6 ParNet模型参数自优化

本文将ParNet 三个流结构中各自所含的RepVGG-SSE模块个数作为3 个待寻优变量，与其余4 个待优化参数：批量大小、学习率、优化器、RepVGG-SSE 模块内部激活函数，分别作为EAOA 中个体的7 个维度进行自适应寻优，各参数的搜索范围如表5 所示。寻优时设置初始化种群数为10，最大迭代次数为5。经EAOA 迭代找到最佳模块数及最优参数，在不降低准确率的前提下，构建出优化后的AParNet 模型，以实现模型轻量化压缩和参数自寻优，模型优化后获得的最优组件如表6 所示。

表5 ParNet模型待优化参数及搜索范围Tab.5 Parameters to be optimized and search ranges of ParNet model

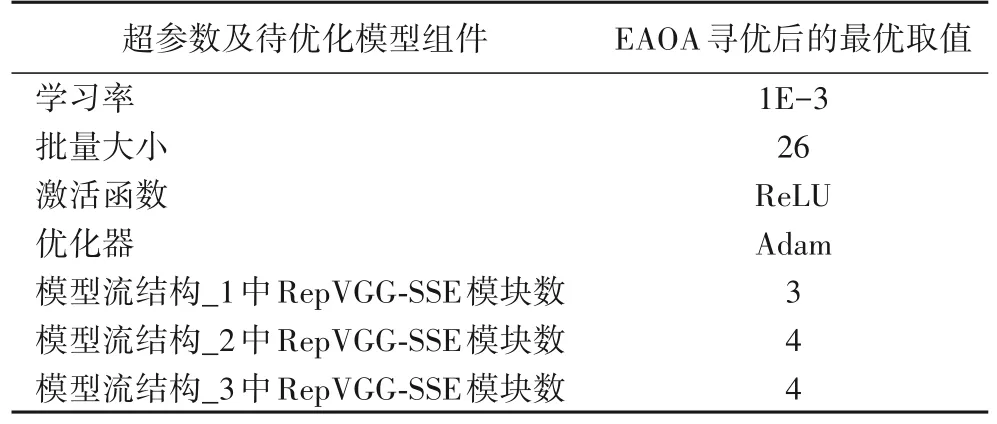
表6 利用EAOA优化后的ParNet最优模型组件Tab.6 ParNet optimal model components optimized by EAOA

为验证本文方法的有效性，对原ParNet 模型和经模型自优化后的AParNet 模型进行性能对比实验，将预处理后划分好的测试集分别输入原ParNet 和AParNet 中，对其中A、B、C、D 四类共760 张图像进行分类验证，结果如表7 所示。

表7 网络模型性能对比实验结果Tab.7 Comparison experiment results of network model performance

实验证明，与原ParNet 相比，本文提出的AParNet 在参数量减少10.8%的情况下，准确率提高到98.6%，且单幅图像测试时间减少了34.8%，模型分类效果更好，且模型深度及测试用时均有所下降。实验结果验证了EAOA 在评价模型自适应寻优方面具备可行性和有效性。

同时，抽取由训练后的AParNet 全连接层输出的特征放入t-SNE 中，得到对分类结果进行可视化的t-SNE 图，如图6所示。根据本文设定的评价结果量化准则，图中的分类结果即对应产学研绩效的4 种评价类型。

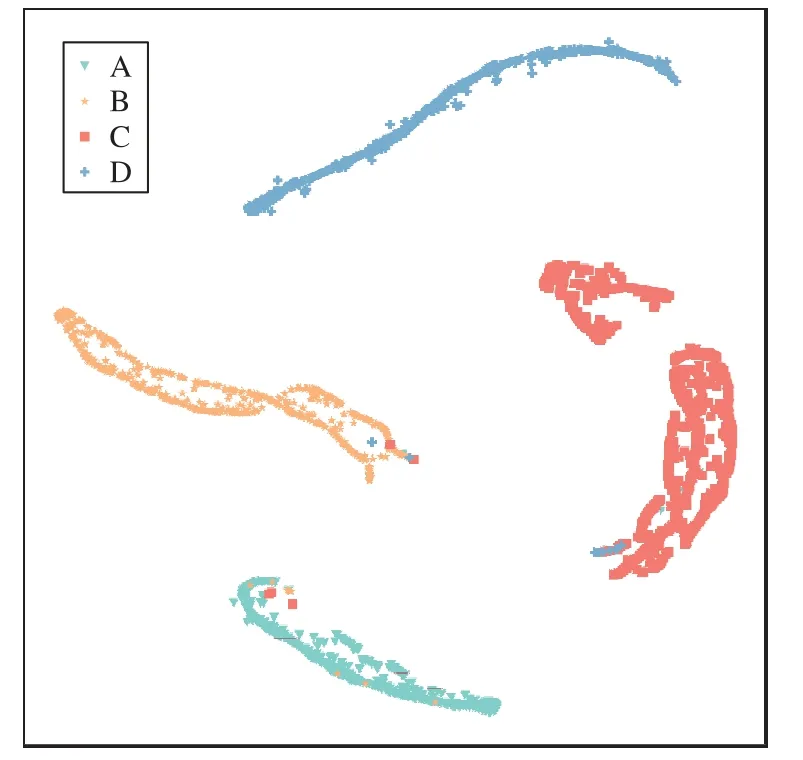
图6 产学研绩效评价结果的t-SNE图Fig.6 t-SNE map of performance evaluation results of industry-university-research

由图6 所示的分类情况可以看出AParNet 的t-SNE 图有很大的类间距离，这代表模型能够以较高的准确率实现分类，即本文提出的AParNet 能够以较高的准确率实现对产学研绩效的智能评价。

5 结语

本文提出了一种基于统计和自适应ParNet 的产学研绩效三级评价体系及智能评价方法。在评价体系方面：分析产学研合作过程中影响绩效的评价要素，设计围绕三方合作主体的评价指标，构建基于模糊数学的数理统计方法且结合主客观综合赋权的产学研绩效三级评价体系，克服了传统产学研绩效评价体系指标涵盖范围较为单一且赋权不够客观的缺点。评价方法方面：首先，为提高离散样本特征表达的丰富度，将离散序列映射至MTF、GADF、GASF 等不同空间域中。实验结果证明，经过多域处理的数据有利于提高深度分类模型的分类精度。其次，设计出面向离散序列深度分类模型高效自适应全局压缩和调参的基于精英反向翻筋斗觅食的混沌优化策略，并结合多分辨率多尺度ParNet 模型构建出AParNet 深度分类模型。最后将AParNet 应用于产学研绩效评价中，在有效压缩模型冗余10.8%的同时，提高分类精度达98.6%，验证了本文方法的有效性。在未来的研究中，为了更深层地把握各指标间的关联性，将引入图结构，以获得更好的评价性能。