基于扩张状态观测器的无人机云台系统控制算法

高胡震，杜昌平，郑 耀

（浙江大学 航空航天学院，杭州 310027）

0 引言

随着技术的不断发展，无人机(Unmanned Aerial Vehicle,UAV)在军事和民用领域得到了越来越广泛的应用。通过挂载各种载荷设备，UAV 能完成各种任务，诸如航拍、侦查、搜救和测绘等［1-2］。UAV 通常通过机载相机跟踪地面或空中的动目标，理想情况下目标需要时刻保持在相机视场的中心。由于UAV 飞行时机身姿态不断变化，且容易受到外界环境的扰动，直接将相机与UAV 固连并不能获得预期的效果，而通过将相机装载在增稳云台上可以抑制无人机机身姿态变化带来的干扰角运动。因此，相机云台系统的控制在目标跟踪任务中起到至关重要的作用［3］。

针对云台系统的控制问题，国内外研究人员提出了各种稳定性算法。李树胜等［4］将三轴平台控制系统简化为3 个单框架子系统，提出了三环复合比例-积分-微分（Proportional-Integral-Derivative，PID）控制方案，包括电流回路、稳定回路和跟踪回路，并验证了平台的稳态精度和动态响应能力；但控制系统的参数较多，参数整定较为复杂。Abdo 等［5］在经典PID 控制的基础上应用模糊控制，设计了一种自调节模糊PID 控制器，在线实时整定PID 参数；但模糊逻辑的设计需要专家经验和大量实验分析，并且模糊规则过多时容易造成规则爆炸。Altan 等［6］采用非线性Hammerstein 块结构对三轴云台系统进行建模，并提出了基于模型预测控制（Model Predictive Control，MPC）算法，实现实时的目标跟踪。Qadir等［7］提出了一种基于视觉的模糊神经网络（Fuzzy Neural Network，FNN）控制方法，将相机的视觉信息作为控制输入，通过FNN 生成云台俯仰和偏航方向的运动以及转速指令，使待追踪的目标时刻保持在画面中心。网络模型首先离线训练，当误差满足要求后再在线训练，以适应空速变化造成的误差。综上，目前UAV 云台控制方法主要分为两个方向：一是经典控制方法，如经典PID 控制以及在它的基础上改进的串级PID 控制和模糊PID 控制。传统PID 控制实现较简单，但参数整定困难，精度难以提升，且对外界扰动的抑制不强；而模糊控制虽然精度较高，但规则设计较复杂。二是智能控制方法，如MPC、FNN 等，这类控制方法对模型精度要求较低，但是对求解器的要求较高，需要大量快速的计算，实时性难以满足。

鉴于此，本文提出一种适用于小型无人机目标跟踪任务的基于扩张状态观测器的串级PID 控制方法。首先，通过姿态解算得到云台在机体坐标系下的姿态角，根据实际姿态角与期望姿态角的误差构建串级PID 控制回路；同时引入扩张状态观测器（Extended State Observer，ESO），估计系统的耦合作用和外界扰动，补偿了控制输入。本文提出的ESO_PID复合控制算法主要有以下优点：

1）通过对角速度的准确估计，避免了强耦合作用带来的复杂动力学建模问题。

2）估计了外界扰动，补偿了输入端，提高了抗干扰能力。

3）算法复杂度低，适合小型无人机目标跟踪任务下的云台控制。

1 机载云台数学模型

机载云台通过基座固连在UAV 上，可绕转轴转动。按照自由度划分，一般可分为二自由度云台和三自由度云台，本文以三自由度云台作为控制对象。云台系统包括基座、偏航框、俯仰框、滚转框和对应电机，其中：基座固连在UAV上；偏航电机安装在基座上，负载偏航框；滚转电机安装在偏航框上，负载滚转框；俯仰电机安装在滚转框上，负载俯仰框，云台相机则安装在俯仰框上。假设云台3 个框架的转轴交点与整个云台系统的质心重合。

1.1 云台系统坐标系

机体坐标系与UAV 固连，它的原点位于云台系统的质心，遵循右手法则。xb轴位于UAV 参考平面内平行于机身轴线并指向无人机前方，yb轴垂直于UAV 参考面并指向UAV 右方，zb轴在参考面内垂直于xbyb平面，指向UAV 下方。

偏航框负责偏航方向的转动。偏航框坐标系与偏航框固连，它的原点位于云台系统的质心，遵循右手法则。当云台偏航角为ψ时，由机体坐标系到偏航框坐标系的旋转矩阵为：

滚转框负责滚转方向的转动。滚转框坐标系与滚转框固连，它的原点位于云台系统的质心，遵循右手法则。当云台滚转角为ϕ时，由偏航框坐标系到滚转框坐标系的旋转矩阵为：

俯仰框负责俯仰方向的转动。俯仰框坐标系与俯仰框固连，它的原点位于云台系统的质心，遵循右手法则。当云台俯仰角为θ时，由滚转框坐标系到俯仰框坐标系的旋转矩阵为：

1.2 机载云台姿态模型

当无人机机动时，由于云台基座与UAV 固连，无人机的姿态会影响云台相机的拍摄。云台相机的姿态角由基座相对惯性空间的欧拉角和云台相机相对基座的欧拉角合成得到。设无人机在惯性空间下的姿态角为[ψθϕ]T，相机云台偏航框、俯仰框和滚转框的转动角分别为ψc、θc和ϕc，即相机云台在机体坐标系下的姿态角为[ψcθcϕc]T，得到由机体坐标系到相机坐标系的旋转矩阵：

通过与UAV 和云台相机分别捷联的陀螺仪，可以实时获得UAV 和云台相机在惯性坐标系下的姿态角。设分别为惯性坐标系到机体坐标系的旋转矩阵和惯性坐标系到相机坐标系的旋转矩阵，且均可通过两组姿态角得到。由惯性坐标系到相机坐标系的旋转矩阵可以表示为：

结合式（4），可得云台三轴的转角为：

故通过机载的陀螺仪测量得到的UAV 姿态角和云台相机姿态角，可以解算出当前云台在三轴方向的转角，即云台在机体坐标系内的姿态角。另外，云台角速度相关的信息也需要进一步解算。

设UAV 机身角速度为ωb，偏航、俯仰和滚转框架的电机角速度分别为ω1、ω2和ω3，则云台相机的角速度在相机坐标系下的描述可以表示为：

可以观察到，由于云台的构造关系，3 个框架的角速度均由两部分构成：一是控制该框架自身转动的角速度；二是上层角速度在自身坐标系下的耦合部分。角加速度的耦合作用则更加复杂。

由此可见，若直接根据系统的运动学模型去设计，3 个通道的耦合作用将使得控制系统变得相当复杂。故将整体系统的设计简化到3 个通道的自抗扰控制上。针对控制器的耦合效应，可以将偏航、俯仰、滚转通道均作为独立的子系统，其他通道的耦合作用可以作为该子系统的外扰作用，通过自抗扰控制的介入对系统的总扰动估计并加以补偿。

2 机载云台控制系

云台系统期望值和反馈值的误差作为控制器的输入、输出控制云台转动，使云台到达期望值。本文设计的云台控制系统面向UAV 目标跟踪的任务场景，控制目标是保持云台相机的视轴指向稳定，且视轴相对目标连线的偏差越小越好，故将云台的姿态角作为控制量，控制器输出各通道电机的控制电压。云台系统的控制结构如图1 所示。

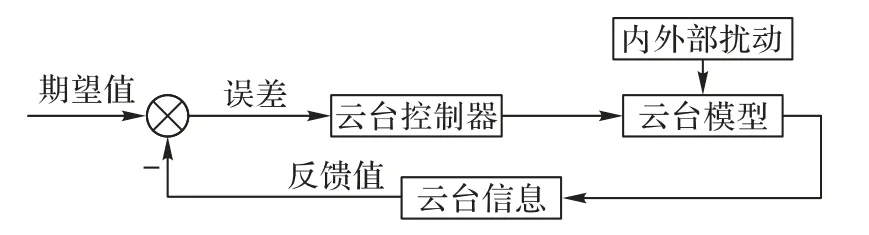
图1 云台系统的控制结构Fig.1 Control structure of gimbal system

2.1 扩张状态观测器

UAV 实际飞行过程中存在许多未知扰动，控制的精度会受到影响。作为自抗扰控制（Active Disturbance Rejection Control，ADRC）的核心部分之一的ESO 可有效抑制外界不确定因素对于系统的干扰，它的核心思想是把能够影响被控输出的扰动作用扩张成新的状态变量，并抑制扰动以将系统线性化，转化为积分器串联型系统进行控制［8-9］。

针对n阶非线性时变系统：

式中：x为系统状态变量，f(x1，x2，…，xn，w(t)，t)为系统的总和扰动作用，w(t)为外扰作用部分，b为控制增益，u为系统控制量。

将未知部分（即系统总合扰动作用）扩张为新的状态量：

则扩张后的系统状态可表示为：

将扩张后的系统状态量的估计值设为Z=[z1z2…znzn+1]T，可以建立如下状态观测器：

原来的非线性系统（9）变成了线性的积分器串联型系统。

饱和函数fal(e，α，δ)是原点附近具有线性段的连续的幂次函数，其增益与误差之间存在类似反比例的关系，目的是在数值仿真时避免高频颤振现象的出现：

其中：e为观测值和状态值的误差；α决定了函数增益的大小；δ与函数线性段的斜率成反比，决定了函数的线性区宽度［10］。

无论函数f(x1，x2，t，w(t))是否连续，是否已知，只要它在过程进程中的实时作用量a(t)=f(x1(t)，x2(t)，t，w(t))是有界的，即参数b已知，总可以选择适当的参数β使ESO 能很好地实时估计对象的状态和被扩张的状态［11-12］。

2.2 PID串级控制原理

PID 控制是一种经典控制方法，以被控对象与期望值的误差为基础，由比例、积分和微分三部分组成。基本的PID控制器算法为：

式中：u(t)为控制器输出；e(t)为系统误差，作为控制器输入；Kp、Ti、Td分别为控制器的比例放大系数、积分时间和微分时间。设u(k)为第k次采样时刻控制器的输出，可得到离散型PID 算法：

通过串级PID 控制云台，分为位置环和速度环：位置环为外环，输入是期望的角度位置，输出是期望的角速度信息并作为内环的输入，采用比例控制；速度环为内环，输入是期望的角速度，负责控制电机转速，采用PI 控制。云台的PID串级控制结构如图2 所示。

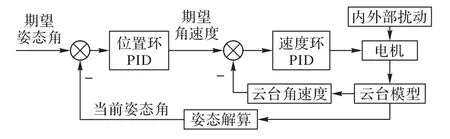
图2 云台PID串级控制结构Fig.2 PID serial control structure for gimbal system

2.3 ESO_PID复合控制算法

PID 控制设计简单，并且对期望目标的跟踪效果良好。但是PID 的控制精度受到系统模型的限制，而工程实际中很难获得系统精确的数学模型，尤其是三轴云台这种强耦合的系统，云台角速度受到其余通道的耦合作用。只有陀螺仪能够实时获取角速度数据，但要得到各通道的角速度信息需要解算机体角速度，过于繁琐。而ESO 可以实时估计不确定系统的各状态量［13］，通过引入ESO 到串级PID 控制系统中，可以对云台的角速度信息做出准确的观测，同时补偿扰动，以提高云台控制系统的控制精度。根据式（7），通过实时采集UAV 和云台相机的姿态信息，可以解算出云台3 个通道的转角，将该转角信息作为ESO 模块的状态值，便可以实时得到准确的角速度观测值。

云台电压与角速度有如下关系［14］：

设耦合角加速度和未知扰动对角加速度的影响合为f，控制增益为b，则各控制通道的状态空间表达式为：

式中：x1为姿态角，x2为角速度。将未知部分f扩张为新的状态量：

则扩张后的系统状态可表示为：

将扩张后的状态量的估计值设为Z=[z1z2z3]T，可以建立如下状态观测器：

当这个系统进入稳态时，方程右端全收敛于0，因此误差系统的稳态误差为：

只要β3足够大于w0，这些估计误差都会足够小［11］。只要扰动有界，总能选取合适的参数来保证ESO 的收敛。

在Simulink 中建立的ESO 模型如图3 所示，k 是Simulink里因为数字太大无法显示自动标注的符号。

2.2.2 专家权威程度 专家对咨询内容的判断依据(Ca)以及对问题的熟悉程度(Cs)进行自评，得出权威程度系数(Cr)，Cr=(Ca+Cs)/2，Cr＞0.7 为可接受程度。本研究中，Ca=0.9861，Cs=0.9139，Cr=0.950。

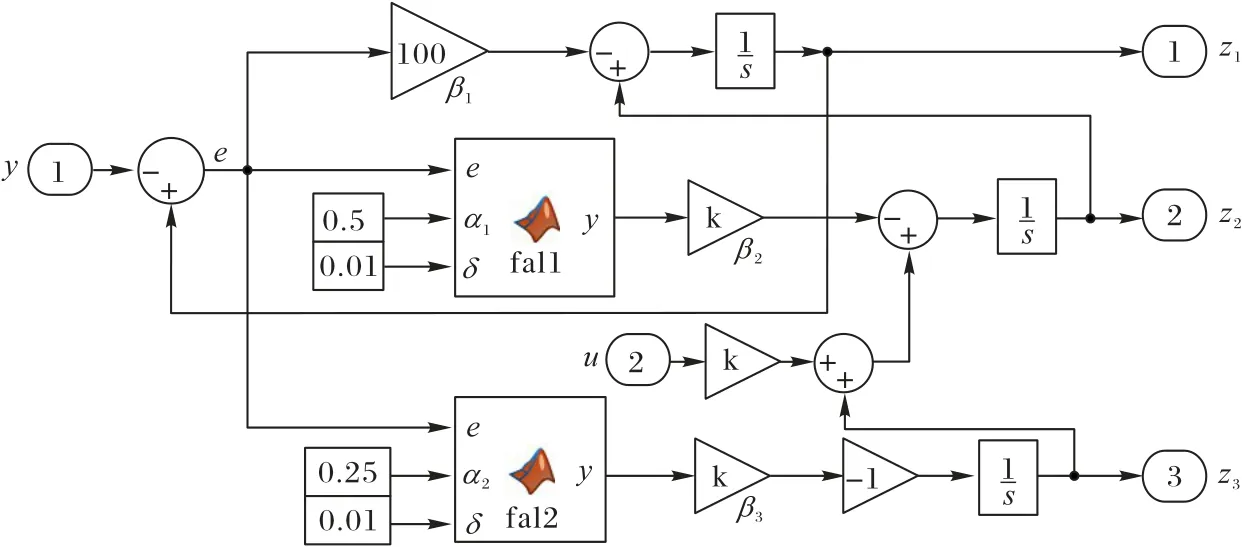
图3 Simulink模型中的ESO模块Fig.3 ESO module in Simulink

将控制量和解算得到的转角信息作为ESO 模块的输入，输出[z1z2z3]T便是对状态量[x1x2x3]T的估计值。

根据式（16）中云台电压和角加速度的关系，通过扩张状态观测器观测到的未知扰动Z3可以用于补偿控制输入：

补偿系数即为ESO 中控制输入增益系数的倒数，参数均可通过查阅电机的相关参数得到。

将ESO 引入串级PID 控制中，可以得到偏航通道下的ESO_PID 复合控制算法，如图4 所示。其中，期望偏航角由姿态解算得到，作为位置环的输入；位置环PID 计算得到期望偏航角速度，作为速度环的输入；速度环PID 计算得到期望的电机电压，经ESO 的输出z3补偿后，作为偏航电机的输入；偏航电机输出对应的转速，经积分环节后与控制输入一同作为ESO 的输入；ESO 的输出z1、z2和z3分别为偏航角、偏航角速度和耦合角加速度的观测量，z2作为速度环PID 的输入，z3作为控制输入的补偿量，构成整体的控制回路。

图4 偏航通道ESO_PID复合控制算法Fig.4 ESO_PID composite algorithm in yaw channel

3 实验验证

本章对ESO_PID 复合算法仿真验证。仿真平台采用Windows 10，CPU 采用Intel 酷睿i7 8700K，仿真环境采用Simulink，针对无人机航拍目标跟踪的任务场景，构建了两类飞行场景，分别对控制算法仿真验证，并和传统PID算法对比。

3.1 算法验证

对ESO_PID 复合控制算法验证。在无指令情况下和给定指令情况下分别验证控制算法的性能，定量指标采用姿态角的均方根误差（Root Mean Squared Error，RMSE）。云台各通道的传递函数［15］为：

根据文献［16］提出的参数β与斐波那契数列的关系，给出了扩张状态观测器参数与仿真步长h的关系：

结合实验，选取了对应的参数β，采用PI 控制，各控制参数根据经验选取。仿真的相关参数如表1 所示。

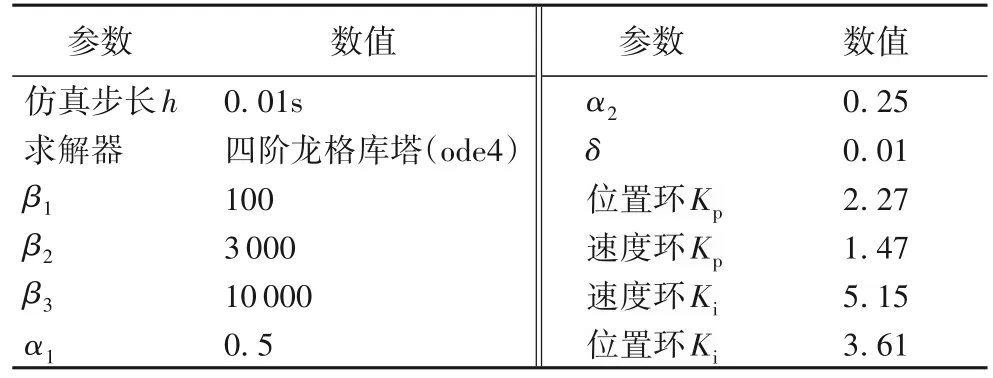
表1 仿真参数设置Tab.1 Simulation parameter setting

3.1.1 无指令情况

考虑无指令情况下，云台仅受到外界随机扰动，在偏航通道下对两种控制算法仿真实验。在控制输入u上添加功率为5，采样时间为0.05 s 的随机白噪声，对ESO_PID 复合控制算法和传统PID 算法的抗干扰能力进行仿真，结果如图5所示，其中，REF 为云台偏航通道的角度随时间变化的期望曲线，由于是无指令情况，期望偏航角始终保持为0°。两种算法的RMSE 分别为0.235 7°和0.771 1°，ESO_PID 复合控制算法相较于传统PID 算法在无指令、随机扰动的情况下偏航通道的角误差降低了69.43%，可见所提算法对外界扰动的抗干扰能力更强。

图5 偏航通道在随机外扰下的角误差Fig.5 Angle error of yaw channel under random disturbance

3.1.2 给定指令情况

给定俯仰通道的期望角信号，仿真验证两种控制算法对它的跟踪能力，同样在控制输入u上添加随机白噪声。两种算法的跟踪效果如图6 所示，其中，REF 为云台俯仰通道的角度随时间变化的期望曲线。两种算法的RMSE 分别为0.631 7°和1.352 5°，ESO_PID 复合控制算法相较于传统PID 算法在给定指令、随机扰动的情况下俯仰通道的角误差降低了53.29%，可见所提算法跟踪的精度更高，角度误差更小。

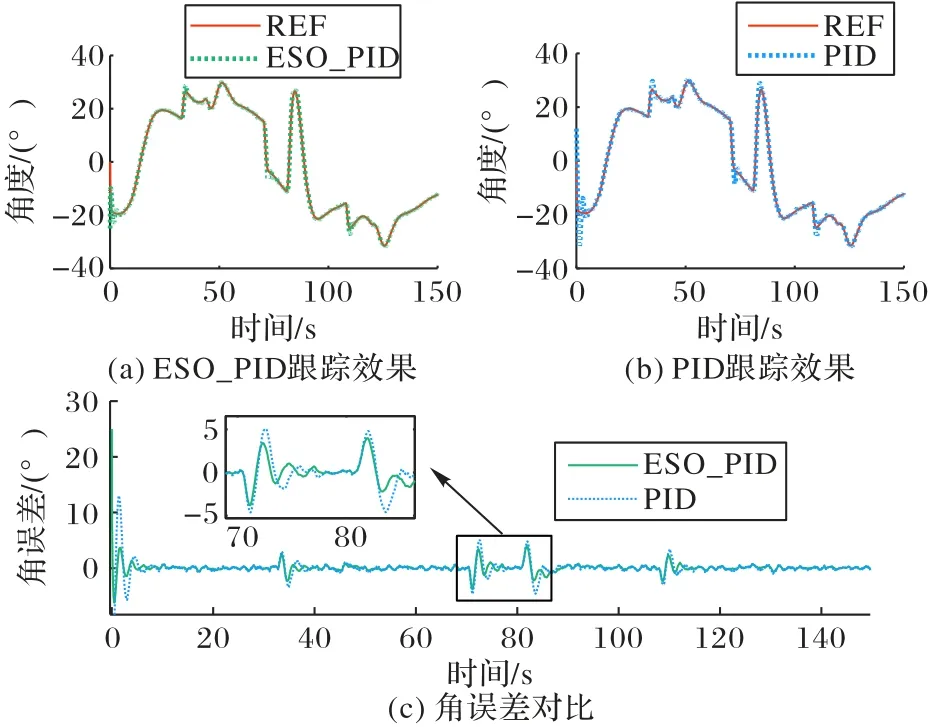
图6 俯仰通道下对给定期望角的跟踪效果Fig.6 Tracking effect of pitch channel under expected angle

通过以上测试，在数值仿真上验证了ESO_PID 复合控制算法的可行性和稳定性。

3.2 飞行场景及参数设置

针对无人机不同的飞行状态，使用Simulink 中无人机工具箱（UAV Toolbox）中的航路点跟随（Waypoint Follower）模块，构建了矩形及圆形的飞行路径，相关航点设置如下，飞行场景的轨迹如图7 所示。

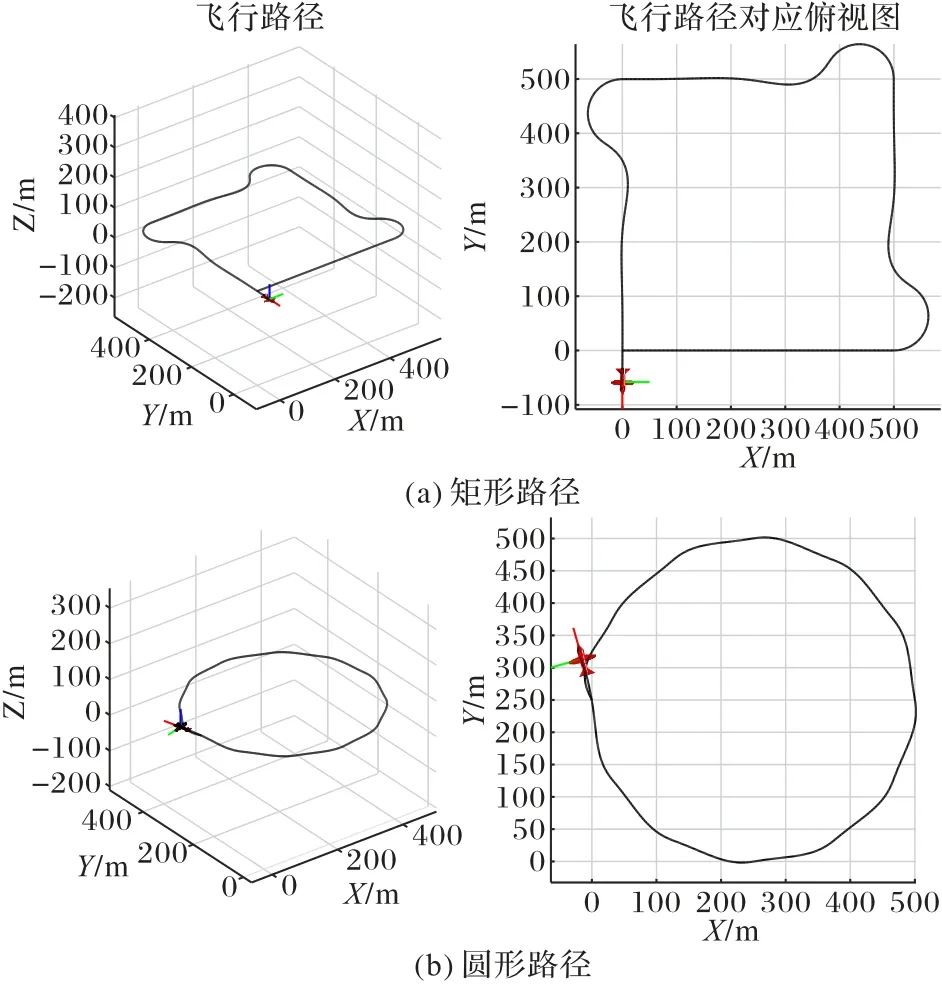
图7 无人机飞行路径及对应俯视图Fig.7 UAV flight paths and corresponding top views

矩形路径航点 ［0，0，50］，［500，0，50］，［500，500，50］，［0，500，50］，［0，0，50］。

圆形路径航点 以［250，250，50］为圆心、250 为半径的圆上均匀分布的12 个点。

根据1.2 节中的姿态解算方法，构建了姿态解算模块，如图8 所示，根据UAV 和云台相机在惯性系中的姿态角测量值，计算出云台相机在相机系下的3 个通道的期望角度ψref、θref和ϕref，作为控制算法的输入，用于仿真UAV 目标跟踪场景下云台控制算法的效果。

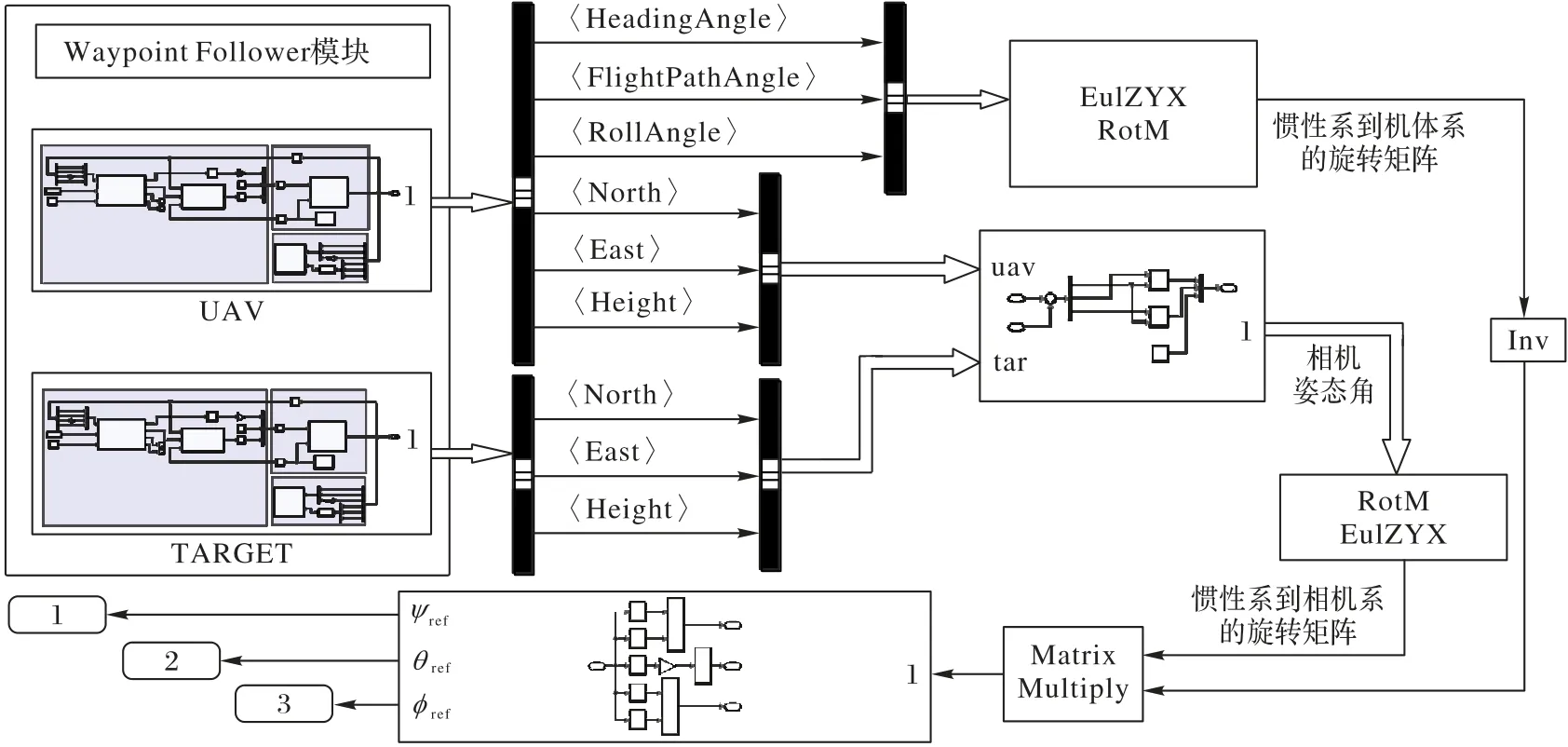
图8 姿态解算模块Fig.8 Attitude calculation module

待跟踪目标的飞行路径也通过航路点跟随模块生成，有直线和盘旋两种飞行情景，与UAV 的两种飞行路径进行组合，可以构建出4 种不同的飞行场景，并对不同的飞行情景仿真。其中，REF 为云台各通道的角度随时间变化的期望曲线。在场景一中，PID 算法在偏航、俯仰、滚转通道的角度RMSE 分别为2.396 8°、1.443 3°、1.156 7°，平均为1.665 6°，ESO_PID 复合控制算法在偏航、俯仰、滚转通道的角度RMSE分别为1.234 3°、0.588 9°、0.597 7°，平均为0.880 70°，控制效果如图9 所示。

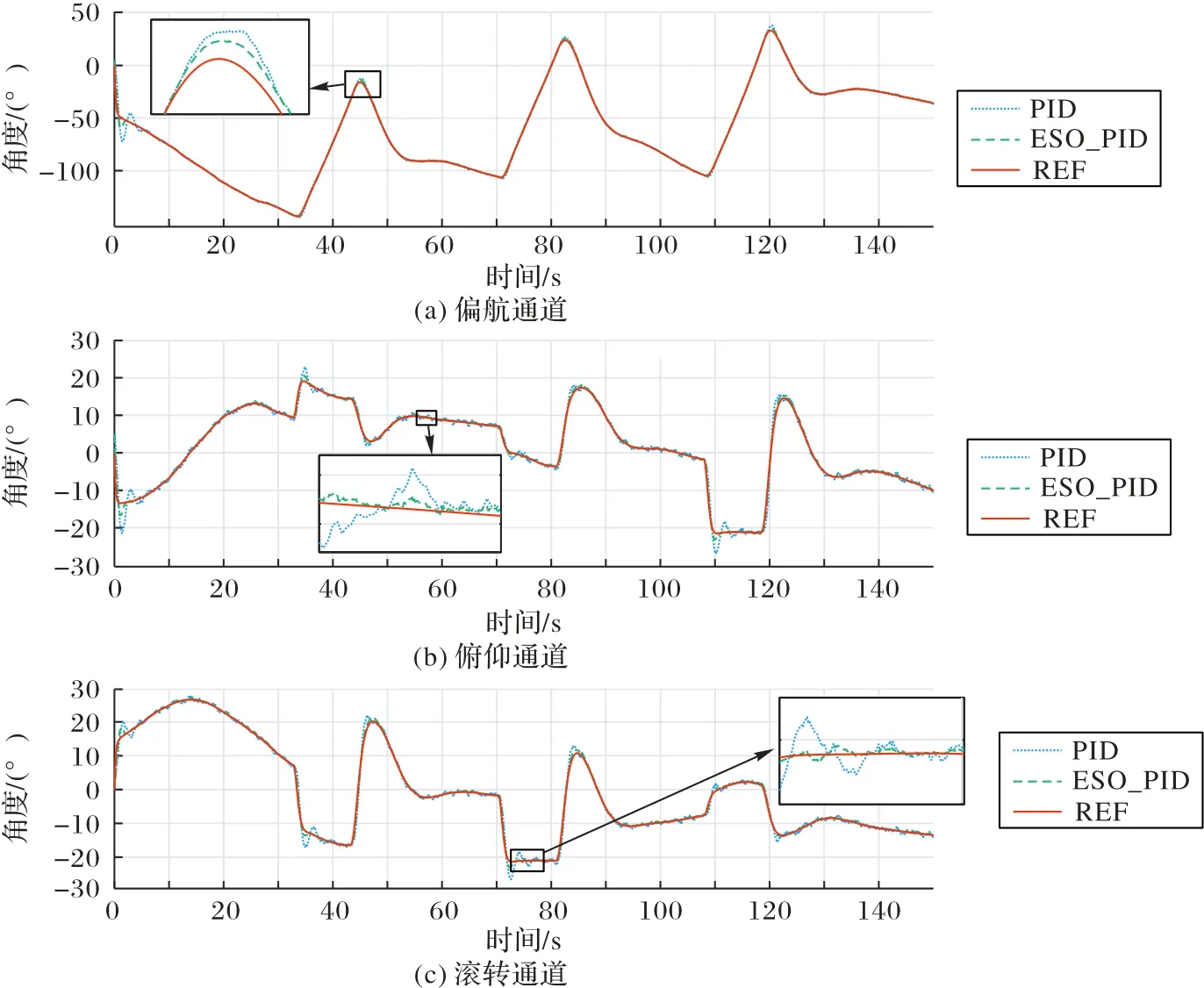
图9 控制方法在场景1中的性能Fig.9 Control performance in scenario 1

两种控制方法的对比结果如表2 所示，其中的误差为偏航、俯仰、滚转三个通道下角度RMSE 的平均值。ESO_PID复合控制方法在各个场景下的平均误差为0.946 3°，相较于传统PID 算法的平均误差1.909 0°，降低了50.43%。

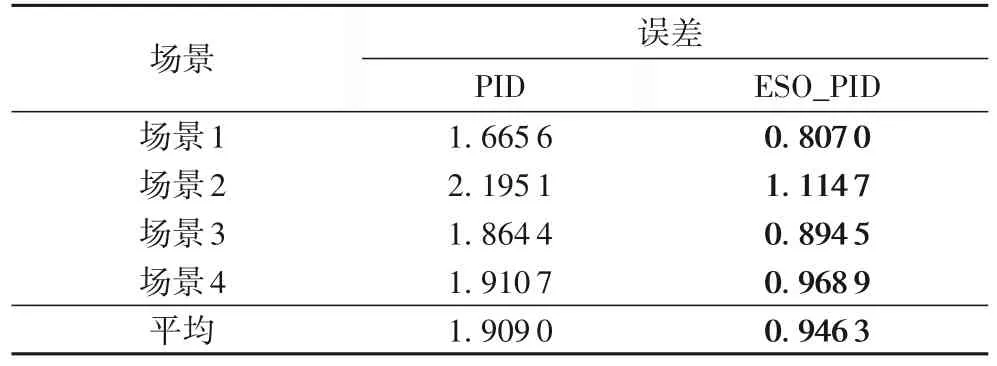
表2 PID与ESO_PID控制结果对比 单位：（°）Tab.2 Comparison of control results among PID and ESO_PID unit：（°）

4 结语

本文提出一种适用于目标跟踪任务的无人机云台控制算法，在串级PID 控制的基础上，结合了扩张状态观测器提高算法的性能。针对三轴云台高度耦合的特性，利用扩张状态观测器观测云台的角速度信息，避免了建立烦冗的数学模型；同时根据偏航、俯仰和滚转各通道的电机参数补偿控制输入。仿真实验表明，ESO_PID 复合控制算法在保证控制精度的同时，大幅提高了系统对外源扰动的抗干扰能力，在不同飞行场景下的表现也比传统控制算法更加优异。

后续的工作中，结合自适应算法调节相关参数，在大误差时提高收敛速度，小误差时提高控制精度，并在实物上验证所提算法的性能。