JIR-Net：用于光声层析图像重建的联合迭代重建网络

候英飒，孙正，2*，孙美晨

1.华北电力大学电子与通信工程系，保定 071003；2.华北电力大学河北省电力物联网技术重点实验室，保定 071003

0 引言

光声层析成像（photoacoustic tomography，PAT）是一种新型的生物医学成像技术。用短脉冲激光作为激励源，生物组织吸收光能量并产生热膨胀，进而激发出宽带超声波（即光声信号）。用超声探测器收集光声信号，通过求解声学逆问题，获得显示成像目标形态结构的光吸收能量分布图或者初始声压分布图（Park等，2022）。在此基础上求解光学逆问题，可以实现定量成像。

常规的PAT 图像重建方法有反投影（back projection，BP）法（Xu 和Wang，2005）、时间反演（timereversal，TR）法（Sun等，2016）、基于傅里叶变换的重建（Fourier transform-based reconstruction，FTR）方法、延迟求和（delay and sum，DAS）法以及迭代重建技术（iterative reconstruction technology，IRT）（Rosenthal 等，2013；Lutzweiler 和Razansky，2013）等。为了简化问题，这些方法通常对成像场景进行理想化的假设。例如：超声波在介质中以恒定的速度进行无损传播，超声探测器被简化成理想的点探测器，能够以足够高的时间和空间采样率在全视角内采集到完备光声信号等。然而，在实际应用中，上述条件往往难以满足。例如：超声波在不同成分的介质中的传播速度通常存在较大差异，在重建图像的过程中，恒定声速（speed of sound，SoS）的假设会导致图像质量明显下降。解决该问题的方法有两种，一是在图像重建中引入有关声速分布的先验知识，补偿由于声速变化引起的测量光声场的像差，改善图像的聚焦效果。此类方法需要已知声速分布的先验知识，然而多数情况下，在进行光声成像前无法获得该先验知识（Huang 等，2013；Haltmeier 和Nguyen，2017）。另一种方法是根据光声信号，同时重建声速分布和初始声压或光吸收能量密度（absorbed optical energy density，AOED）分布，无需有关声速的先验知识（Zhang等，2008；Matthews 等，2018）。目前的主流方法是采用基于模型的迭代框架，即选择适当的优化策略，迭代求解前向成像模型的逆问题（Huang 等，2016；Sun 和Sun，2021）。此类方法的重建精度很大程度上依赖于有关成像目标的先验假设模型。为了降低问题的病态程度，需要合理选择正则化方法及其参数。此外，求解过程非常耗时。

近年来，深度学习已成为医学成像领域的研究热点（唐朝生 等，2021；李书林 等，2022）。为了减轻逆问题求解中的病态，使用有监督学习进行图像重建也成为该领域的最新技术，主要包括非迭代学习法和学习迭代法两类（Farnia 等，2020；Guo 等，2021）。按照深度神经网络输入和输出的不同，非迭代学习法分为信号增强、图像增强和优化重建3 类（Lan 等，2019b，2021）。信号增强是采用“信号”到“信号”的转换思路，利用深度学习技术提高原始光声信号的信噪比，然后采用常规方法重建图像（Awasthi 等，2020）。图像增强采用“图像”到“图像”的转换思路，首先采用常规方法重建初始图像，然后用神经网络对初始图像进行优化（Vu 等，2020；Sun和Yan，2020）。这类方法的成像质量受到初始重建精度的限制，而采用常规方法重建图像时，可能无法恢复原始信号中隐含的细节信息。特别是当探测器在有限角度内采集到不完备的光声信号时，采用该方法很难完整地恢复出扫描盲区中的结构。优化重建方法是利用神经网络直接学习“信号”到“图像”的映射（Guan 等，2020）。网络的输入是原始信号或预处理后的信号，输出是高质量图像（Lan 等，2019a；Kim 等，2020）。此类方法需要利用全连接或大卷积核的卷积神经网络解决输入信号矩阵的非对称性问题，难以获得复杂目标的准确重建（Guo 等，2021；Lan等，2020）。

学习迭代法是将迭代重建技术与深度学习相结合，神经网络从训练数据中学习得到先验约束，用于优化迭 代过程（Adler 和Öktem，2017；Shan 等，2019）。例如：利用神经网络训练正则化工具（Antholzer等，2019；Li等，2020），或者通过深度梯度下降（deep gradient descent，DGD）进行迭代更新（Boink 等，2020；Sun 等，2021），确保每次迭代都收敛于最优值。相较于传统的迭代重建技术，学习迭代法可以通过更少的迭代获得更高质量的图像。但是由于神经网络需要从训练数据中学习先验约束，因而此类方法的时间成本较高，训练数据的质量也会对成像结果产生影响。

本文搭建一个基于学习迭代策略的联合迭代重建网络（joint iterative reconstruction network，JIRNet），根据有限角度稀疏光声信号，同时重建AOED分布图和声速分布图，解决由于不完备测量数据和不均匀声速导致的图像质量下降问题。采用仿真、仿体和在体数据训练和测试网络。通过与传统非学习方法、非迭代学习方法和基于DGD 的学习迭代方法比较，证明在稀疏测量和组织声学特性不均匀情况下，该方法重建光声图像的优势。

1 基于迭代梯度网络的联合重建方法

基于学习迭代策略搭建卷积神经网络模型，将AOED 和声速的梯度下降信息融入到网络的训练中，通过反向传播梯度下降求解非线性最小二乘问题，实现从不完备光声信号到高质量AOED 分布图和声速分布图的映射。

1.1 成像模型

短脉冲激光照射组织、成像平面内的AOED 与入射光辐射通量和组织光吸收系数之间的关系为

式中，A(r)和μa(r)分别是成像平面中位置r处的AOED 和光吸收系数，Φ(r)是光辐射通量。组织中的光吸收体基于光声效应产生的初始声压为

式中，p0(r)是初始声压，Γ是热膨胀系数。光声信号在组织中的传播用如下波动方程描述，具体为

式中，p(r，t)是位置r在时刻t的声压（pressure），I(t)是入射激光脉冲能量函数，c(r)是声速（speed of sound，SoS），βe和Cp分别是组织的等压膨胀系数和一定压力下的比热容。

从AOED到产生声压的过程用算子表示为

式中，p是到达探测器表面的声压矩阵，A是AOED矩阵，H(c)是与声速c有关的算子。

求解如下非线性最小二乘问题，根据声压信号同时重建AOED和声速分布，具体为

1.2 JIR-Net的结构

如图1 所示，JIR-Net 的输入是在成像平面内采集的声压信号矩阵和预先设置的常数声速，输出是AOED分布图和声速分布图。

图1 本文方法流程图Fig.1 Flow chart of the proposed method

如图2 所示，网络由4 个结构单元组成，每个单元的输入是前一个单元输出的AOED 分布图、归一化声速分布图以及二者的梯度。一个单元由特征提取、特征融合和重建3个模块组成，如图3所示。

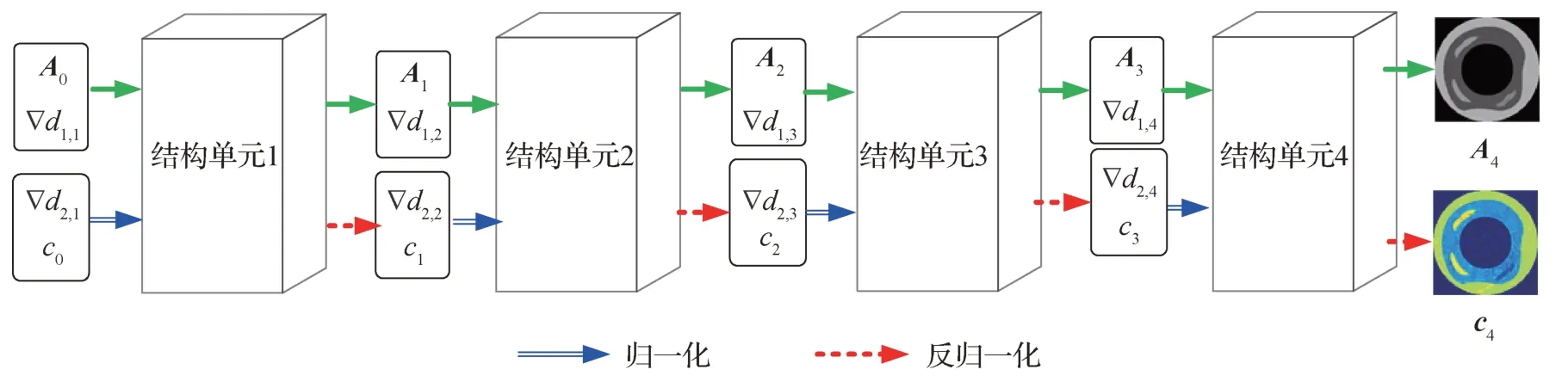
图2 JIR-Net结构示意图Fig.2 Architecture of JIR-Net

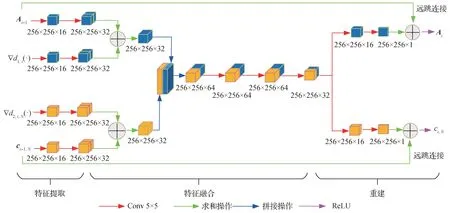
图3 结构单元示意图Fig.3 Schematic of a structural unit

特征提取模块分别对4 个输入进行两次滤波核尺寸是5 × 5 ×S、步长为1的same卷积，S是当前层输入的特征图数量，四路输入的特征通道数均为16。

特征融合模块的作用是：将AOED 分布图及其梯度进行像素值求和，将归一化声速分布图及其梯度进行像素值求和，然后将得到的两个特征图沿通道维度拼接起来，并进行3次卷积操作。

重建模块通过两次卷积操作，得到AOED 和声速的更新值，并通过远跳连接，将该单元的输入与当前层输出的更新值进行像素值求和，最后的ReLU激活函数保证更新后的AOED 和速度分布是非负分布。

第i个结构单元输入的AOED梯度为

式中，pk是训练集中第k个样本输入的声压信号测量值，Ai-1，k和ci-1，k分别是经过i-1次迭代后第k个样本输出的AOED 估计值和反归一化后的声速估计值。为方便起见，文中将∇d1，i[pk，H(ci-1，k)Ai-1，k]简写为∇d1，i(⋅)。

声速梯度利用伴随波动方程求得。伴随波动方程的表达式（Huang等，2016）为

式中，q(r，t)是伴随波，s(r，t)是伴随源，具体为

式中，rl是探测器的第l个测量位置，L是探测器测量位置的总数，(rl，t)是探测器在位置rl处时刻t测得的声压，p(rl，t)是声压理论值，由式（3）求得，δ(r-rl)是狄拉克函数。式（7）的初始条件为

式中，T是采集信号的时间长度。根据式（3）和式（7）得到声速的梯度，具体为

根据式（10）计算第i个结构单元中声速的梯度∇d2，i[pk，Η(ci-1，k)Ai-1，k]，对其归 一化后 表示为∇d2，i，N[pk，Η(ci-1，k)Ai-1，k]，简写为∇d2，i，N(⋅)。对第i个单元输入的声速分布ci-1归一化，记为ci-1，N。

1.3 数据集

1.3.1 计算机仿真数据集

建立包含不同组织成分的计算机仿真模型，其中4 个模型的几何结构如图4 所示，并设置其组织特性参数，如表1 所示。采用蒙特卡罗方法模拟入射光在组织中的传输，得到成像平面中的光辐射通量（Wang 等，1995）。进而根据式（1），由光辐射通量和光吸收系数得到AOED（absorbed optical energy density）。采用MATLAB k-Wave 工具包仿真得到探测器接收的光声信号（Treeby 和Cox，2010），其中加入30 dB 的高斯随机噪声。探测器采样频率和中心频率分别设置为250 MHz 和5 MHz。将不同稀疏度的仿真光声信号和常数声速共同作为样本输入，将仿真AOED 分布图和预设的声速分布图作为期望输出，构建数据集。部分样本示例如图4 所示。

表1 仿真模型的组织特性参数Table 1 Characteristic parameters of simulated phantoms

图4 仿真数据集中的样本图像示例（Amp·表示幅值Amplitude，a.u.表示任意单位arbitray units）Fig.4 Examples of samples in simulation datasets

构建了3 个由不同稀疏度仿真信号和不同常数声速作为样本输入的仿真数据集，如表2 所示。用“（视角，采样率）”表示数据稀疏度，如（180°，0.7）表示扫描角度是180°、采样率为0.7。将每个数据集中的样本随机打乱，按照6∶3∶1 的比例划分为训练集、验证集和测试集，利用验证集选择最佳网络模型。

表2 仿真数据集的构成Table 2 Description of simulation datasets

1.3.2 仿体数据集

制作了14 个包含不同嵌入物的柱形仿体，不同材料的声速和光吸收系数如表3 所列，制作细节如表4所列，部分仿体实物照片如图5所示。

表3 制作仿体的不同材料的声速和光吸收系数Table 3 SoS and absorption coefficients of different materials used to fabricate phantoms

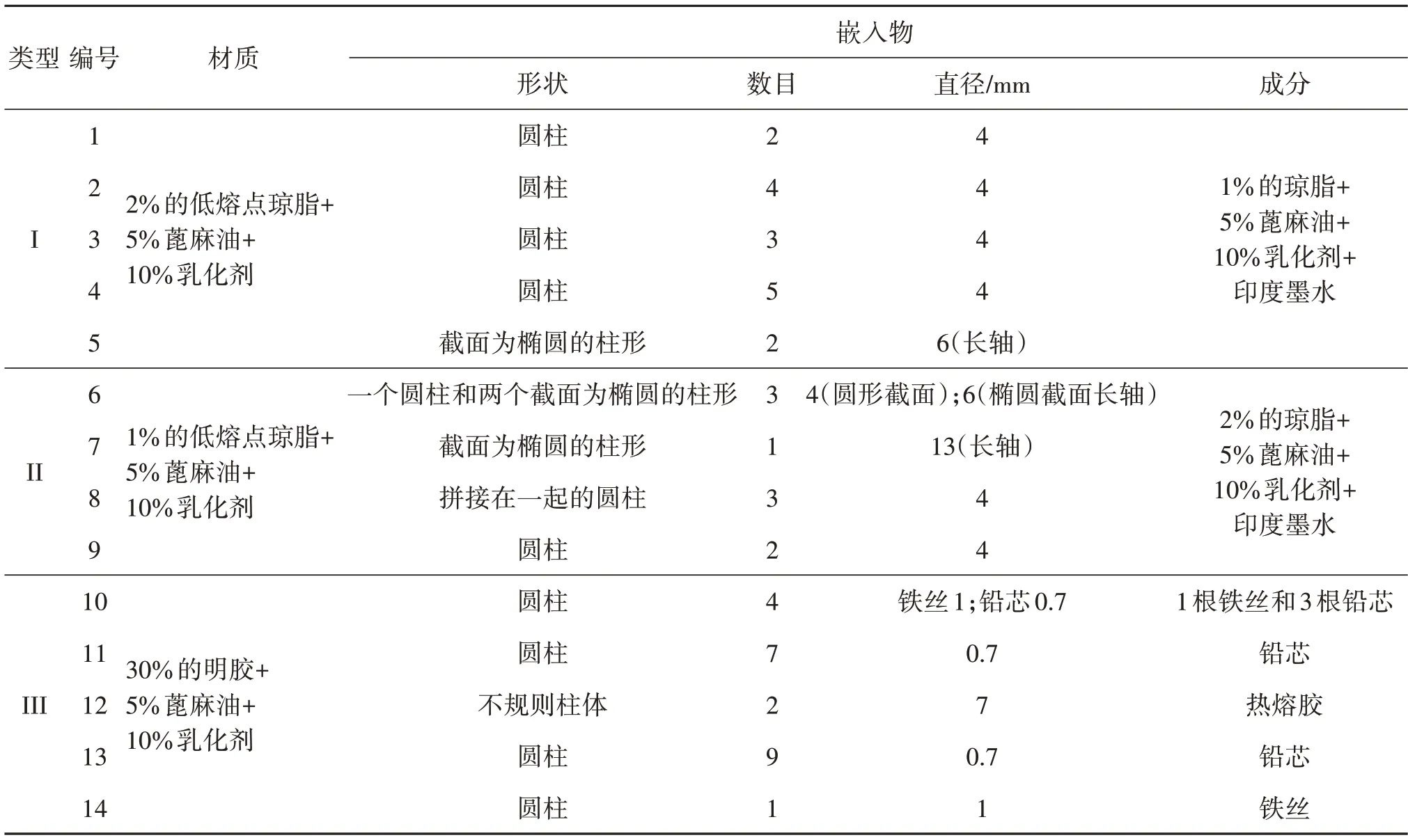
表4 仿体的构成Table 4 Composition of phantoms

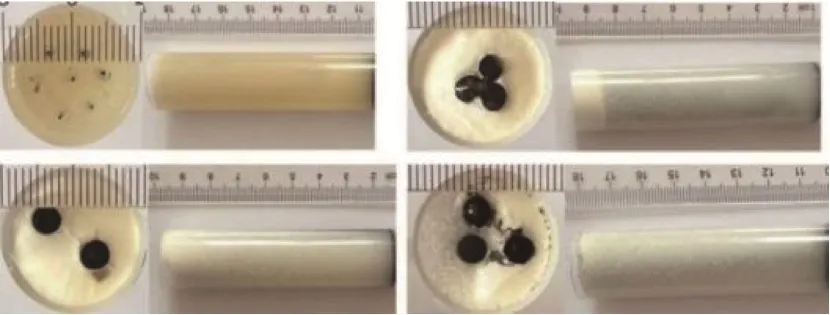
图5 仿体实物照片Fig.5 Photos of phantoms

每个仿体的总长均为80 mm，横截面直径为20 mm。用于采集仿体光声信号的成像系统采用Nd：YAG 激光器输出的全波波长（680～900 nm）可调谐激光作为光源，脉冲重复率是10 Hz，脉冲宽度是7 ns，最大脉冲能量是120 mJ。超声探测装置由256个中心频率为5 MHz、带宽为60%的聚焦超声换能器阵元，排列成覆盖角度为270°的环形阵列。对每个仿体的扫描长度约为10 mm，对4个仿体（即表3中编号为I-1、I-3、II-8 和III-11 的仿体）得到的28 个扫描切片构成测试集，对其余10个仿体得到的69个扫描切片构成训练集。样本输入的常数声速均为1 500 m·s-1。为了避免产生过拟合，采用数据增强技术（包括随机翻转、旋转和平移等）对训练集进行扩增，最终的训练集中包含4 140个样本。

1.3.3 在体数据集

在体数据集由对活体小鼠进行全身扫描采集的光声信号构成。成像系统采用Nd：YAG 激光器输出的715 nm、730 nm、760 nm、800 nm、850 nm 可调谐激光作为光源，在730 nm 处的最大入射脉冲能量约为70 mJ，脉冲重复率是10 Hz，脉冲宽度是8 ns。超声探测装置是由128个中心频率为5 MHz、带宽为60%的聚焦超声换能器阵元构成的环形阵列。利用前述每种波长的激光对俯卧位小鼠进行全身扫描，共获得244 个切片，其中200 个切片数据用做构建训练集，44个切片构建测试集，样本输入的常数声速均设置为1 500 m·s-1。增强后的训练集中包含4 392个样本。

1.4 训练网络

采用自适应矩估计（adaptive moment estimation，Adam）梯度下降法（Kingma 和Ba，2017）沿各层参数梯度方向逐个单元进行参数优化。第i个单元的损失函数为

式中，L1，i和L2，i分别是第i个单元重建AOED分布图（即任务1）和声速分布图（即任务2）的损失函数，具体为

式中，M是样本总数，Atrue，k和ctrue，k，N分别是第k个样本期望输出的AOED 分布图和归一化声速分布图，Ai，k和ci，k，N分别是 第i个单元 输出的 第k个样本 的AOED估计值和归一化声速估计值，具体为

设置学习率为0.001，批处理大小为batch size=64，epoch=200。损失函数曲线如图6 所示，可见随着epoch 的增加，损失函数值逐渐减小，当epoch >200时，变化趋于平缓。

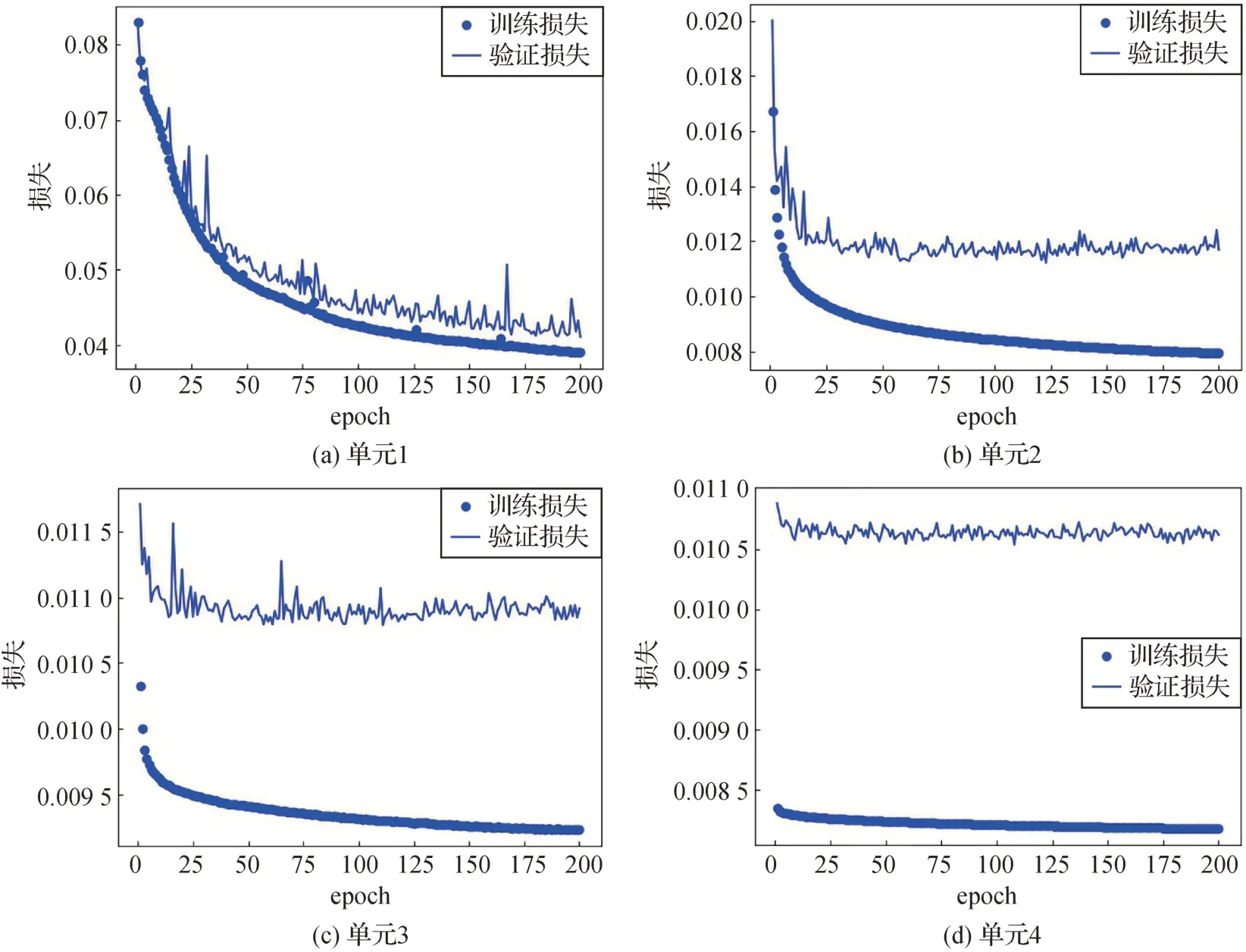
图6 采用稀疏度为（180°，0.9）的仿真数据集训练JIR-Net时，4个结构单元的损失函数曲线Fig.6 Loss of the four structural units when JIR-Net is trained using the simulation dataset with a sparsity of（180°，0.9）（（a）Unit 1；（b）Unit 2；（c）Unit 3；（d）Unit 4）

2 方法的性能评价

分别采用计算机仿真、仿体和在体成像数据定量评价JIR-Net 根据不完备光声信号重建图像的性能。仿真和仿体实验的目的是在已知目标特性参数真实值的情况下，定量评估重建精度，并讨论算法中的相关参数对其性能的影响。在体实验的目的是验证JIR-Net在真实场景中应用的可行性。

将JIR-Net 与经典TR 法（Sun 等，2016）、交替优化（alternative optimization，AO）法（Sun 和Sun，2021）、U-Net 后处理法（Sun 和Yan，2020）（简称U-Net）和DGD 网络（Sun 等，2021）进行比较。AO 法是通过交替优化迭代求解信号测量值和理论值之间误差最小的非线性最小二乘问题。U-Net 后处理法是将采用TR 法重建的低质量图像作为U-Net 的输入，最终输出优化后的图像。DGD 网络共包含5 个结构单元。采用相同的数据集训练JIR-Net、DGD 和U-Net，JIR-Net 和DGD 的训练参数为batch size=64和epoch=200。U-Net 的训练参数为batch size=1和epoch=200。U-Net、DGD 和JIR-Net 的训练时间分别约为2.4 h、6.5 h和17 h。

在仿真实验中，以仿真AOED 分布图和预设的声速分布图作为标准图像，采用峰值信噪比（peak signal noise ratio，PSNR）和结构相似度（structural similarity，SSIM）作为定量指标，评价重建图像质量。重建图像和标准图像之间的SSIM 越大，PSNR 越高，表明重建质量越佳。仿体和在体实验中，由于无法获得AOED 的真实值，因此采用对比度（contrast ratio，CR）和对比 噪声比（contrast-to-noise ratio，CNR）（单位：dB）作为量化指标评价AOED 图像质量。CR衡量图像灰度反差的程度，CNR是图像中有用信号区域和背景区域之间对比度的度量。CR 和CNR 越高，表示重建图像质量越好。此外，仿体实验中，不同材料的声速真实值是已知的（如表4 所列），因此采用PSNR和SSIM定量评价声速分布的重建精度。在体实验中，仅通过光声扫描无法获得声速的真实值，因此采用视觉评估定性评价声速分布的重建质量。

实验中，仿真、TR 和AO 法实现的编程环境是MATLAB（R2016a，the Math Works，Inc.，Natick，Massachusetts），计算机配置为12th Gen Intel（R）Core（TM）i5-12500H CPU、16 GB RAM和Windows 11 64 位操作系统。神经网络的搭建、训练和测试的运行环境为Ubuntu 16.04，所用GPU是NVIDIA公司生产的GeForce 3090Ti，显存为16 GB。操作系统是Ubuntu 16.04，编程语言是Python 3.7，深度学习框架是TensorFlow 2.6.0和Keras 2.0。

3 实验结果与分析

分别对计算机仿真、仿体和在体3 种成像数据对网络性能进行测试，并对实验结果进行分析。

3.1 仿真实验结果

对于不同稀疏度的仿真光声信号，分别采用不同方法重建图像的结果如图7所示。由图7可知，在全角度扫描时，信号的采样率越低，AO和TR重建图像的整体亮度也越低，这是由于在稀疏采样时将未探测到的声压设为零造成的。采用深度学习方法重建图像的视觉效果和评价指标明显优于AO 和TR法。当采样率较高时，3个网络都可以重建出较高质量的图像。但是当采样率较低时（如0.3 和0.1），JIR-Net 重建图像的质量则明显优于DGD 和U-Net。而且JIR-Net重建图像的质量并没有随着信号采样率减小而明显降低，这表明经过训练的JIR-Net对测量信号的稀疏度具有一定的鲁棒性。当进行有限角度扫描时，TR重建质量随着扫描角度的减小而降低，角度越小，盲区越大，图像中目标结构缺失的部分就越多。与TR相比，虽然AO和U-Net可以在一定程度上改善图像质量，但是随着扫描角度的减小，其能够补全的盲区也越少。DGD虽然可以补全盲区，但由于假设声速恒定，与真实声速分布并不相符，因此存在目标严重变形的问题。而采用JIR-Net重建的图像，无论视觉效果还是评价指标均优于其他方法，且扫描角度越小，优势越明显。180°扫描时，JIR-Net重建图像的SSIM 比DGD 高约8.4%，比U-Net 高 约18.3%，PSNR比DGD高约17.4%，比U-Net高约74.7%。

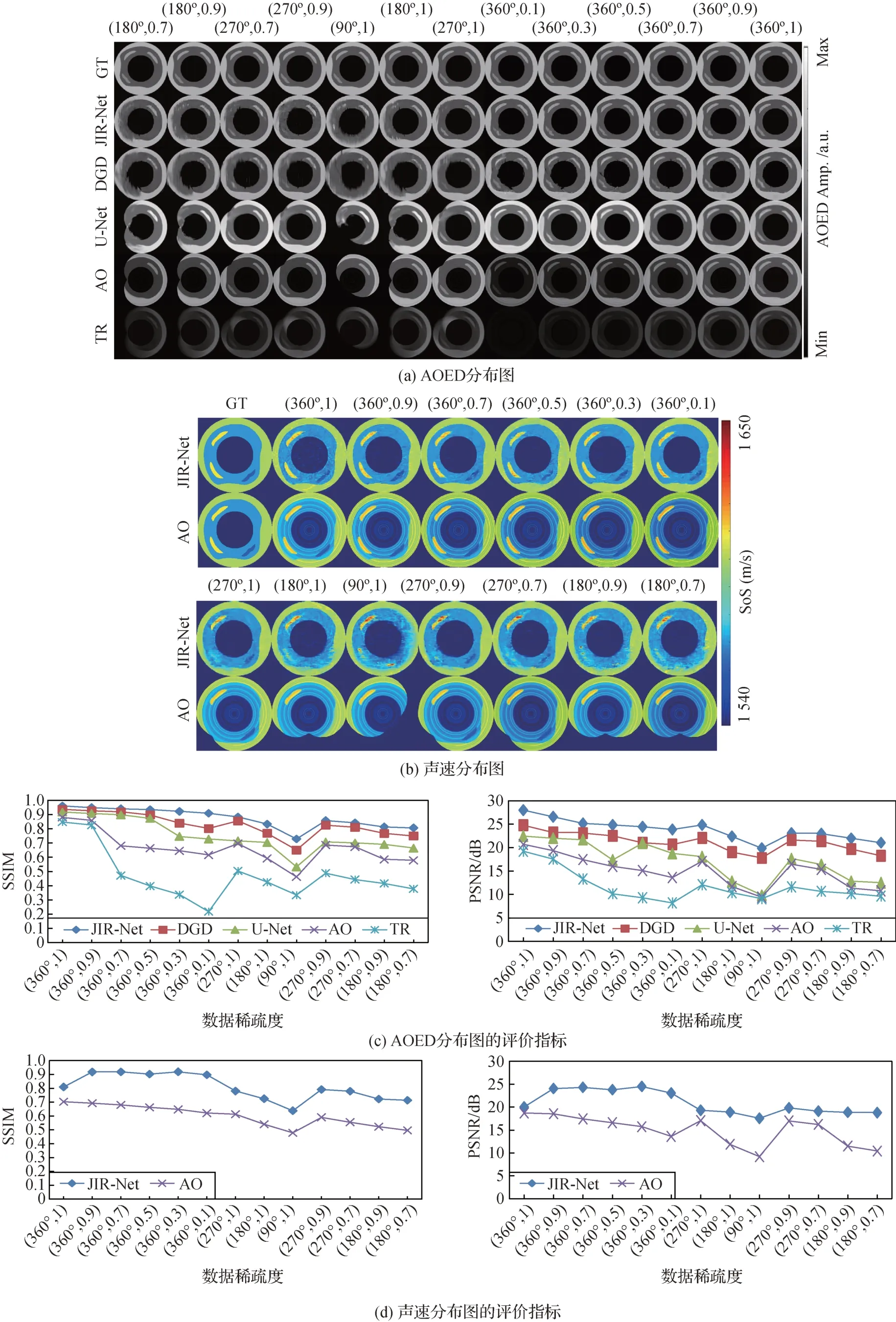
图7 根据不同稀疏度的仿真信号重建图像的结果Fig.7 Results of image reconstruction from simulated signals with different sparsity（（a）AOED images；（b）speed of sound images；（c）AOED metrics；（d）SoS metrics）

3.2 仿体实验结果

对仿体的图像重建结果如图8 所示，与实物照片对比，采用5 种方法重建的图像都能够可靠地显示嵌入目标的位置。但是采用AO 和TR 法重建图像的整体亮度明显低于3 种深度学习方法重建的图像。在DGD、U-Net、AO和TR重建图像中，可以清晰地观察到嵌入物周围的伪影。而JIR-Net 重建的图像具有最佳的视觉效果和最高的对比度。

图8 仿体的图像重建结果Fig.8 Results of image reconstruction of phantoms（（a）AOED images；（b）SoS images；（c）AOED metrics；（d）SoS metrics）

3.3 在体实验结果

图9 是包含复杂结构的活体小鼠4 个头部和胸腹部切片的成像结果。由图9 可知，与仿真和仿体实验结果类似，采用AO 和TR 法重建图像的整体亮度以及横截面边缘的对比度都明显低于深度学习方法重建的图像。在JIR-Net 重建图像中，箭头标示细节结构的对比度明显高于采用其他方法重建图像的对比度。这证明了在重建复杂目标方面，JIR-Net 优于非学习方法以及DGD 和U-Net方法。

图9 在体小鼠实验中的图像重建结果Fig.9 Results of image reconstruction for in vivo mice（（a）AOED images；（b）SoS images；（c）AOED metrics）

4 讨论

结合仿真实验结果，分析讨论初始声速以及网络结构单元个数对重建图像质量的影响。并对所提方法相对于其他成像方案的优势和不足进行讨论。

4.1 初始声速对重建图像质量的影响

为了分析初始声速对JIR-Net 性能的影响，在其他条件不变的情况下，分别设置初始声速为1 404 m·s-1、1 449 m·s-1、1 500 m·s-1和1 716 m·s-1。对全角度密集采样仿真光声信号进行图像重建，结果如图10所示。

由图10 可知，当采用不同的初始声速时，JIRNet重建图像的视觉效果和评价指标变化并不显著。由表1 可知，本文建立仿真模型时，将不同组织成分的平均声速设定在1 540～1 650 m·s-1范围内。当初始声速与实际声速比较接近时（如1 500 m·s-1），JIR-Net、DGD、U-Net 和AO 重建图像的质量差别不大，且明显优于TR法。随着初始声速与实际声速的差别增大，JIR-Net 相较于其他方法表现出明显的优势。例如，当初始声速为1 716 m·s-1时，远大于光声信号传播过程中的实际声速。此时，TR 重建中声波的反演时间变短，导致重建出的目标区域不完全，且存在严重畸变。将TR 重建图像作为U-Net 的输入时，输出的图像质量也没有得到明显改善。对于DGD 网络，由于所设初始声速与真实值差别较大，每次求解梯度时均会产生误差，逐次迭代后误差累积，导致图像中的畸变严重。此外，由图10（b）（d）可知，不同初始声速条件下，JIR-Net 重建声速的精度优于AO法，SSIM和PSNR可分别提高约34.4%和22.6%。

4.2 结构单元数对网络性能的影响

为了分析JIR-Net 中的结构单元数对网络性能的影响，在其他条件和参数不变的情况下，分别将结构单元数设定为1、2、3、4 和5。对稀疏度为（180°，0.9）的仿真光声信号进行图像重建，评价指标如图11 所示。由图11 可知，结构单元数越少，重建图像质量越低。增加结构单元数虽然会改善图像质量，但也会导致网络训练时间明显延长，如表5 所示。当单元数大于4 时，重建图像的评价指标变化趋于平缓，表明此时再增加结构单元也不会显著改善图像质量，但是训练时间会大幅延长。因此，本文最终采用4 个结构单元构成JIR-Net。

表5 JIR-Net由不同数量结构单元组成时的训练时长Table 5 Time cost in training JIR-Net consisting of different number of structural units

图11 当JIR-Net包含不同数量的结构单元时，根据稀疏度为（180°，0.9）的仿真信号重建图像的评价指标Fig.11 Evaluation metrics of images reconstructed from the simulated signal with the sparsity of（180°，0.9）when JIR-Net consists of different numbers of structural units

4.3 所提方法相对于其他成像方案的优势和不足

JIR-Net 采用学习迭代框架实现有限角度稀疏测量条件下的高质量图像重建。与非迭代学习方法相比，这种方案以牺牲时间成本为代价获得了高质量的成像结果。训练JIR-Net 单个结构单元的时间约为DGD 的2.6 倍，U-Net 的7 倍。采用训练后的JIR-Net、DGD 和U-Net 重建一帧256 × 256 像素的图像，所需的时间分别为18.4 s、14 s和9 s。时间成本的主要差别在于JIR-Net 和DGD 需要计算AOED 和声速的梯度，而U-Net不用。

此外，通过同时重建AOED 分布图和声速分布图，本文方法解决了由于不均匀声速所致图像质量下降的问题。该方法不需要任何有关成像目标的先验知识。与基于模型的非学习方法相比，成像质量和精度不依赖于前向模型，无需对成像目标和场景进行理想化的假设，可直接应用于不同的扫描几何和成像场景。

5 结论

本文提出一种联合迭代重建网络，通过将AOED 分布和声速分布的梯度下降信息融合到网络训练中，实现利用不完备光声信号重建高质量图像的目的。仿真、仿体和在体实验结果表明，采用该网络重建的AOED 分布图，其视觉效果和评价指标均优于经典TR 方法、AO 方法、基于U-Net 的非迭代学习方法和基于DGD 的学习迭代方法。而且光声信号测量数据的稀疏度越低，优势越明显。讨论结果表明，所提方法的重建精度对初始声速不敏感，具有较好的稳定性。网络结构单元个数对重建精度有一定的影响，虽然增加结构单元可以提高重建质量，但是也会进一步增加时间成本，需要在图像质量和时间成本之间做出权衡。

在未来的工作中，将从以下3 个方面改善网络性能：1）构建规模更大、质量更高的数据集，尽可能多地包含可能观察到的图像特征，并使仿真训练集适应使用真实光传播模型生成的图像。2）进一步优化网络结构并改进训练策略，以更快的速度重建更高质量的图像。3）改变网络输入信号的类型，对原始光声信号测量数据进行预处理后再送入网络，提高网络的学习效率。

致谢：本项工作中活体小鼠光声成像数据的采集得到了中国医学科学院药物研究所的支持，仿体成像数据的采集得到了北京化工大学的支持，在此表示感谢。