同面阵列电极敏感场优化方法
2024-03-20温银堂张玉燕宗乐文
温银堂, 王 凯, 张玉燕, 宗乐文, 潘 钊
(燕山大学 电气工程学院,河北 秦皇岛 066004)
1 引 言
近年来,随着科学技术不断发展,异物检测技术越来越受到社会重视。在工业、农业生产中,不经意间混入的异物轻则导致经济损失[1,2],重则威胁到人身安全。常用的异物检测技术有超声检测、红外热像检测等方法[3,4],而由于某些材料具有强吸声和低导热等特性,导致部分检测方式失效。与其他测量技术相比,同面电容成像检测技术[5]是一种利用电场边缘效应的无损检测手段,其检测能力基本不受被测材料特性的影响,而且它还具有响应快、安全性高、非侵入式测量和可视化成像等特点。同面电容检测技术广泛应用于海关安检、地雷探测和轨道站台检测等,该技术已经受到研究人员的广泛重视,被视为过程成像领域内一个新的研究重点[6]。
目前国内外主要从传感器设计[7,8]、敏感场仿真[9,10]和图像重建算法改进[11~15]等方面展开研究来优化电容成像技术。Tholin-Chittenden C等[7]将电容层析成像技术应用于非金属材料的地雷探测,研究并设计出5种同面电容传感器,并分析了5种传感器的检测精度和深度;孙玉容等提出了一种FTP算法,通过减小伪影和改善边界处的模糊程度来提高图像的质量;曹鹏鹏等提出了一种基于FCM数据优化的成像算法,减小了电容误差对介电常数的影响,提高了胶层缺陷重建图像的精度;Ye等为了减小“软场”特性的影响,提出了一种扩展灵敏度矩阵的参数优化方法,提高了重建图像的质量和稳定性[9];孙启国等通过对比在重建图像过程中考虑和忽略软场效应的情况,说明了忽略软场效应会降低重建图像的精度和质量[15];赵玉磊等提出一种基于双粒子群协同优化的算法,通过消除了因忽略软场效应而产生的影响来提高成像精度[14]。
图像重建的准确性决定了电容成像技术能否成功应用,而重建图像的精度和质量受到软场效应的影响。软场效应是指介质与敏感场的变化为非线性关系,其中敏感场的负灵敏度加剧了敏感场的非线性,因此优化负灵敏值对于重建图像显得非常重要。
在同面电容层析成像过程中,会在计算敏感场灵敏度值时会引入负灵敏度值,导致电场线发生畸形,当负灵敏度大于正灵敏度时会使重建图像失真。吴云提出负灵敏度的危害以及设想方案,但并未给出针对负灵敏度值的解决方案[16]。因此本文针对负灵敏度会导致重建图像失真的问题,提出了一种数据降维并结合平方增敏的方法,通过增强电容数据、敏感场数据的有效性以及减弱敏感场矢量求解造成的特征边缘波动性来提高重建图像的质量,降低敏感场的非线性特性导致重建过程存在严重的不适定性,并通过实验验证了所提方法的有效性。
2 同面电容成像原理
电容敏感机理是当电容器被激励时,它会产生一个静电场来感应介电常数分布并反馈为电容值。图1(a)所示为平行板电容器的电场分布示意图,由于电场的边缘效应,极板边缘的电场线呈开口状,从板间区域扩展到外部空间。由于边缘电场具有更好的延展性,因此设计出同面电容器[17],如图1(b)和图1(c)所示。其中图1(b)展示的是均匀介电常数中同面电容器的电场线分布情况,电场线基本为光滑1曲线;而图1(c)中的圆球则是检测目标,具有与周围不同的介电常数的特性,电场线在介电常数变化的交界处出现明显1弯曲,此处即为电场的软场效应。
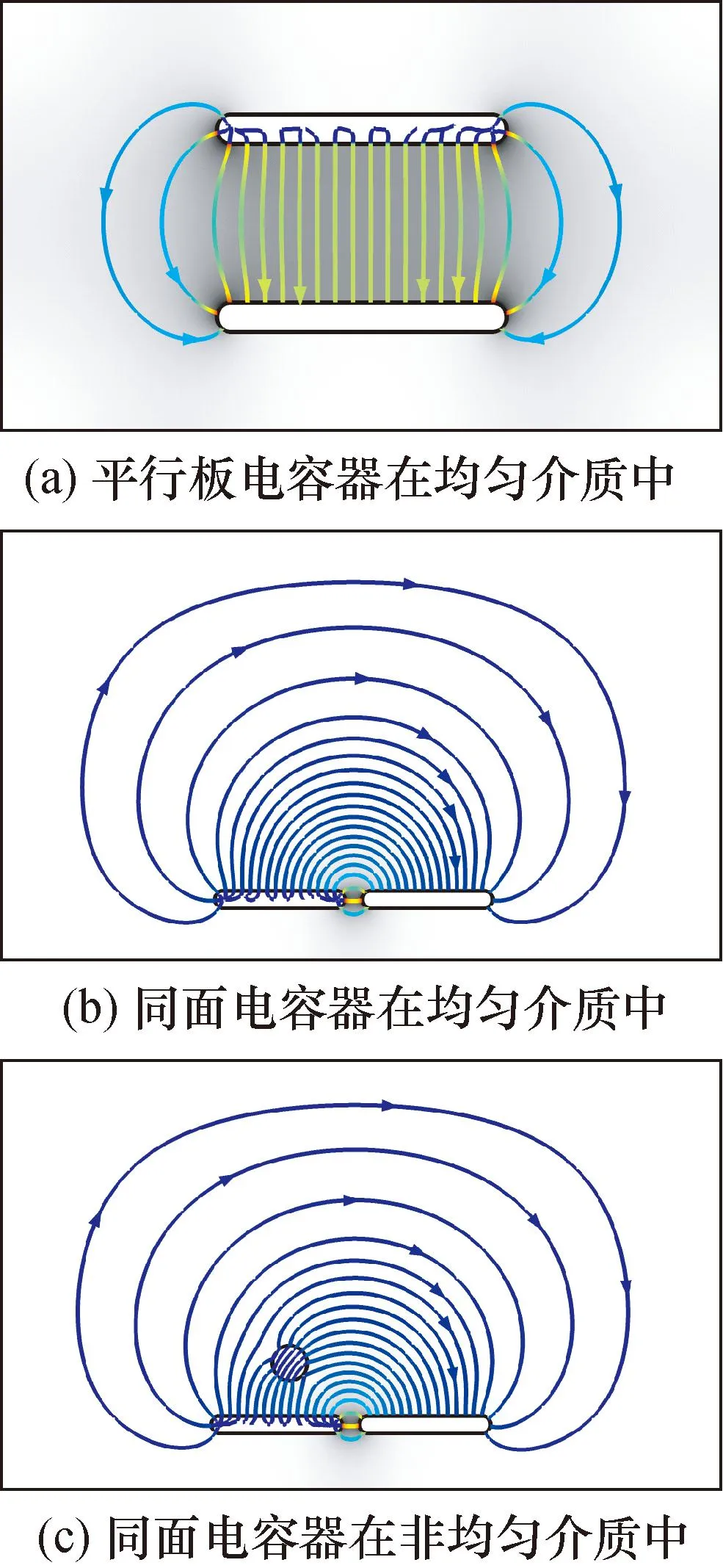
图1 电容传感器电场分布示意图Fig.1 Schematic diagram of capacitive sensor electric field distribution
电场取决于介电常数的分布,并随介电常数的变化而变化,反过来说介电常数的分布信息蕴含在电场信息中。依据电磁场理论,电容成像系统的静电场可由泊松方程进行描述。如式(1)所示:
·(εφ)=-ρ
(1)
式中:φ表示电位;ε示相对介电常数;若场中无自由电荷,ρ值为0。
通过电场的泊松方程,结合边值问题中的狄利赫里问题和高斯通量定理可得到求解电极对电容值的表达式,如式(2)所示:
(2)
式中:V为两电极板间的电位差;Γ为电极的表面。
再将式(2)离散化和归一化,可得到电容成像的数学模型:
C=SG
(3)
式中:C为电容值矩阵,其数据量由传感器的电极数决定;G为介电常数矩阵;S为灵敏度值矩阵,表示电容受介质影响,记为敏感场。灵敏度值矩阵的维度取决于电极对数和敏感场域的离散单元数。
敏感场[18]的灵敏度值可通过有限元的电势分布法求解得到,具体的计算公式为:
(4)
式中:Ei(x,y,z)表示电极i为源电极时,坐标(x,y,z)处体素的电场强度;Vi表示电极i的激励电压;Ω(x,y,z)为坐标(x,y,z)处体素的体积。
介电常数矩阵G理论上可由电容值矩阵C与灵敏度值矩阵S的逆矩阵直接反演得到。但灵敏度值矩阵的行列数不等,因此不存在逆矩阵。实际上,介电常数值矩阵一般是借助重建算法公式来近似求解,本文采用的是Tikhonov正则化算法,其重建公式为:
G=(STS+μIn)-1STC
(5)
式中:μ为正则化参数;In为单位矩阵,其维度与敏感场矩阵的列数保持一致;ST为S的转置矩阵。由于μ值越大,正则化程度越高,重建图像会越模糊,为保证重建图像具有较好的清晰程度,因此设置正则化参数为0.01。
3 同面阵列电容敏感场优化方法
本文的研究是基于同面3×4阵列电容成像系统,传感器结构如图2所示。传感器的整体参数为160mm×160mm×20mm;传感器内部的极板参数为 40.7mm×29.8mm×0.1mm,传感器的底部屏蔽为150mm×150mm×2mm,电极间距为3mm,电极的极间屏蔽和外部屏蔽均为1mm。被测物中,较大的圆直径为 30mm,较小的圆直径为20mm,厚度均为2mm,介电常数为3.5。在边缘效应影响下,边缘电场信号微弱,且易受干扰。为让电场更集中地分布在极板上侧,传感器在电极间和边缘部分设置了屏蔽来减弱侧向极板电场的影响,在极板底部设置了屏蔽来减小电场能量的损失。同面3×4阵列电容传感器每次检测都可以采集到66个独立电容数据,所以电容值矩阵的维度为66×1。
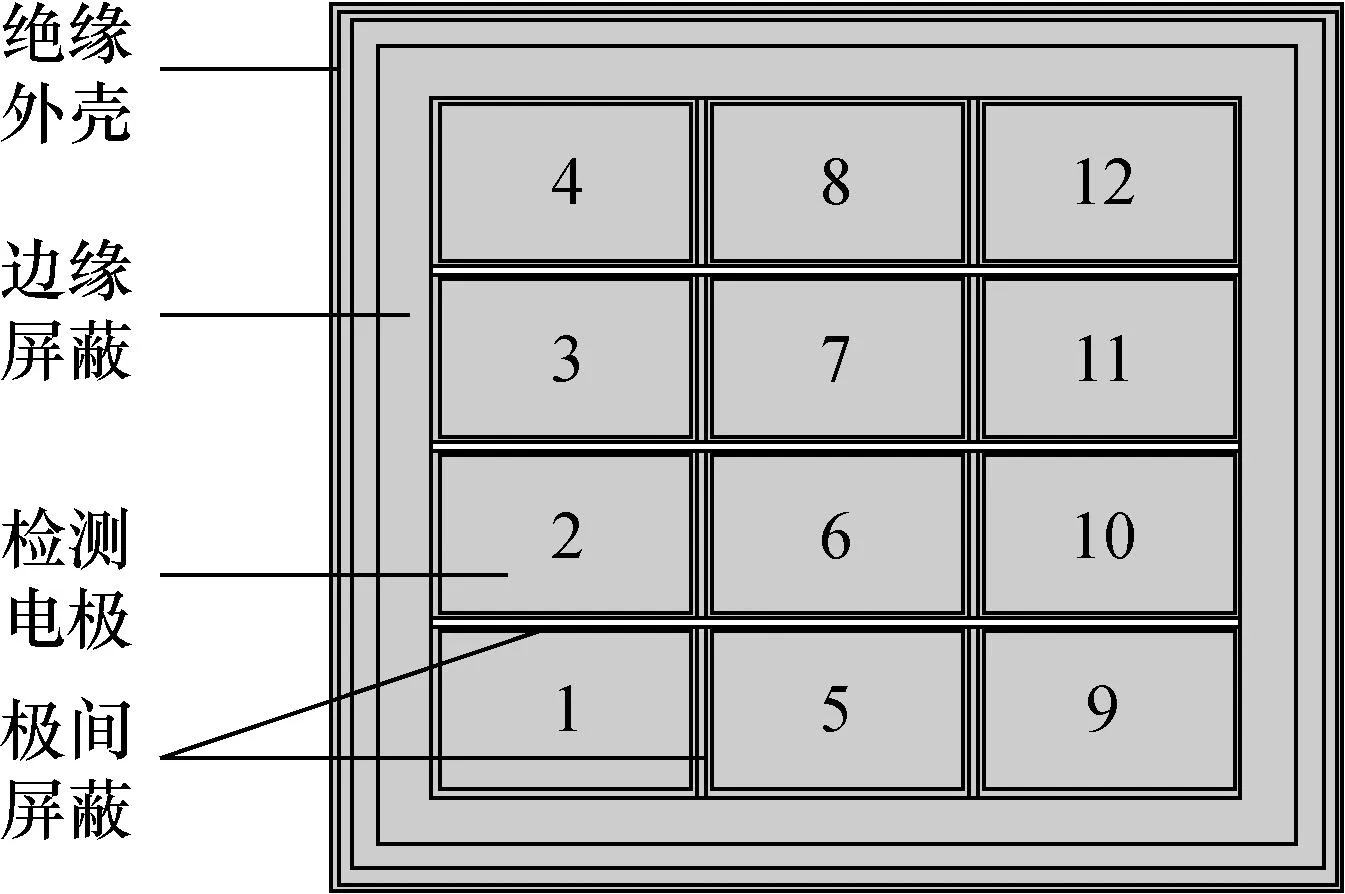
图2 同面3×4阵列电容传感器模型Fig.2 Coplanar 3×4 array capacitive sensor model
考虑到边缘电场信号微弱且易受干扰的因素,可能致使电极对的电容值误差波动性较大,于是重建计算利用电容变化量作为参数来减小环境和仪器误差造成的影响。要补充说明的一点是,电容变化量在参与计算前要经过归一化处理,而依据电容变化量并通过重建公式计算得到的是介电常数变化量矩阵,它与介电常数矩阵具有相同的数据分布特征,因此也可根据它重建出介质分布图像。
为得到电容变化量数据,电容传感器在实际检测时,首先要标定空满场。本文拟定当传感器上方介质为空气时,记为空场,当传感器上方为大于空气介电常数的均匀介质时,记为满场。另外,将介质为目标检测对象时,记为测量场。
敏感场拟定为极板上方150mm×150mm×50mm的矩形域,离散为60×60×20个单元,各单元体积为2.5mm×2.5mm×2.5mm。同面3×4阵列电容传感器的每个电极对都对应一组敏感场灵敏度值,记为子敏感场。其维度与敏感场划分的单元数相同,所以灵敏度值数据为72 000个。由于同面3×4阵列电容成像系统的12电极可组合出66个同面电极对,因此传感器全局敏感场的数据维度为66×72000。
3.1 基于最大熵的敏感场数据降维方法
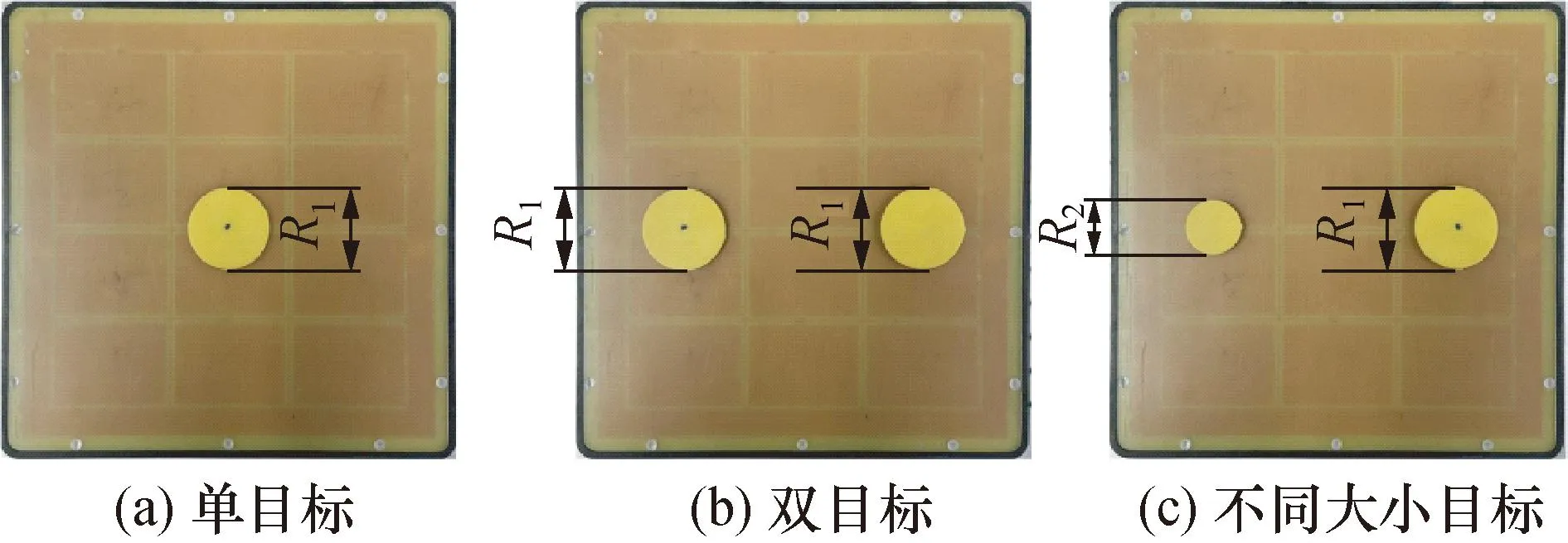
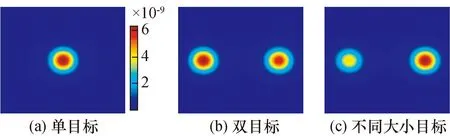
电容数据是由传感器直接检测得到,因此数据真实可靠[19],本文以电容数据作为研究切入点。首先对电容数据的特征进行分析,在有限元软件COMSOL中构建出多组模型,如图3所示。图3(a)为单目标检测的仿真模型;图3(b)为双目标检测的仿真模型;图3(c)为不同大小目标检测的仿真模型。从图4(a)中可以看到,相较于标定电容数据,测量电容数据中存在一个明显变化的电容数据,并且该电容数据对应的电极对恰好为目标对象所在的电极对。图5(a)为电容变化量数据归一化后的柱状图,相较电容值数据,电容变化量数据可以突出目标对象的特征电容数据该电容变化量值远远大于其他电极对的电容变化量值。图4(b)和图5(b)为双目标模型仿真得到的电容数据图,图4(c)和图5(c)为不同大小目标模型仿真得到的电容数据图。从图中可以看出,同样只有目标对象所在电极对的电容值有明显的变化量,因此基本上可以通过电容变化量就可以清晰的判断目标对象所在的位置。
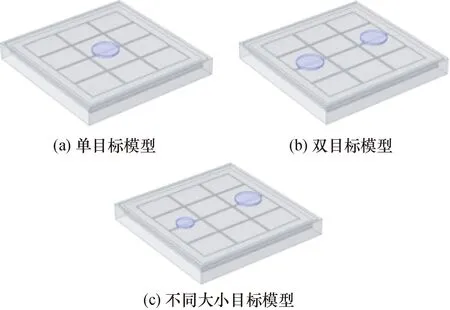
图3 目标检测仿真模型图Fig.3 Target detection simulation model diagram

图4 标定电容值与测量电容值折线图Fig.4 Line chart of calibrated and measured capacitance value

图5 电容变化值柱状图Fig.5 Capacitance change value histogram
从电容变化量柱状图可推断出,由于非特征电容数据远远小于特征电容数据,因此它们基本上对图像重建过程没有贡献,即无效数据。若将它们代入重建公式计算,可能加剧重建过程的不适定性进而导致重建图像质量与稳定性更差。因此本文提出一种基于最大熵原理的数据分割方法,通过筛选特征数据的方式,一方面减少计算量,提高成像速度;另一方面降低重建过程的不适定性。最大熵的熵是用于衡量一个分布的均匀程度,熵越大表示分布越均匀。
对于模型(a)而言,66个电容变化量数据中只存在着一个有效数据,当该有效数据被单独划分到一个分布时,数据的熵和达到最大,即实现了数据的分割。具体的推导公式如下,首先利用直方图统计的方式对数据分类,假定直方图数为L,则有:
(6)
假设分割阈值为t,阈值将直方图分割后,可获得两个分布A与B,A=(X∈1,2,…,t),B=(X∈t+1,t+2,…,L)。A,B中随机变量的概率分布为:
(7)
P(B)=1-P(A)
(8)
另外,概率分布为P(X)的离散型随机变量X,其熵公式为:
(9)
则A,B两个分布的熵为:
(10)
(11)
t值遍历(X∈1,2,…,L),当H(A)+H(B)取得最大值时,t值即为最大熵法的分割点。相对于其他分割方法,最大熵分割不会忽略弱有效数据的信息,可以保留对象更多的信息。
电容变化量数据中小于t的数据即为无效数据,将剔除无效数据的电容矩阵记为记为C*。
C*=[ci,…,cj](1≤i≤j≤66)
(12)
电容成像的关键是电容和敏感场。由于敏感场灵敏度值是依据有限元电势分布法仿真进行计算,但是对于未知介质分布的目标对象,实际上无法构建模型仿真计算得到最真实的敏感场,因此一般都是利用空场灵敏度值矩阵近似计算。如图6所示为空场敏感场的三维图示,它包含了所有电极对子敏感场的信息,虽然它也能实现介质分布图像重建,但对于不同的目标检测模型,采用同一敏感场可能会影响重建图像的质量和稳定性。考虑到特征电容数据实际上已经实现了对于目标对象的定位,而敏感场数据与电容数据存在对应关系,因此通过将特征电容数据作为索引就可以实现对敏感场数据的自适应降维。降维后的敏感场中只保留了特征子敏感场,记为特征敏感场。理论上特征敏感场相对于空场敏感场减少了无效信息,从而保证重建图像不受无效信息的干扰,进而提升稳定性。将特征敏感场的灵敏度值矩阵记为Sc,其表达式如公式(13)所示:

图6 空场敏感场三维图Fig.6 3D diagram of the sensitive field in the empty field
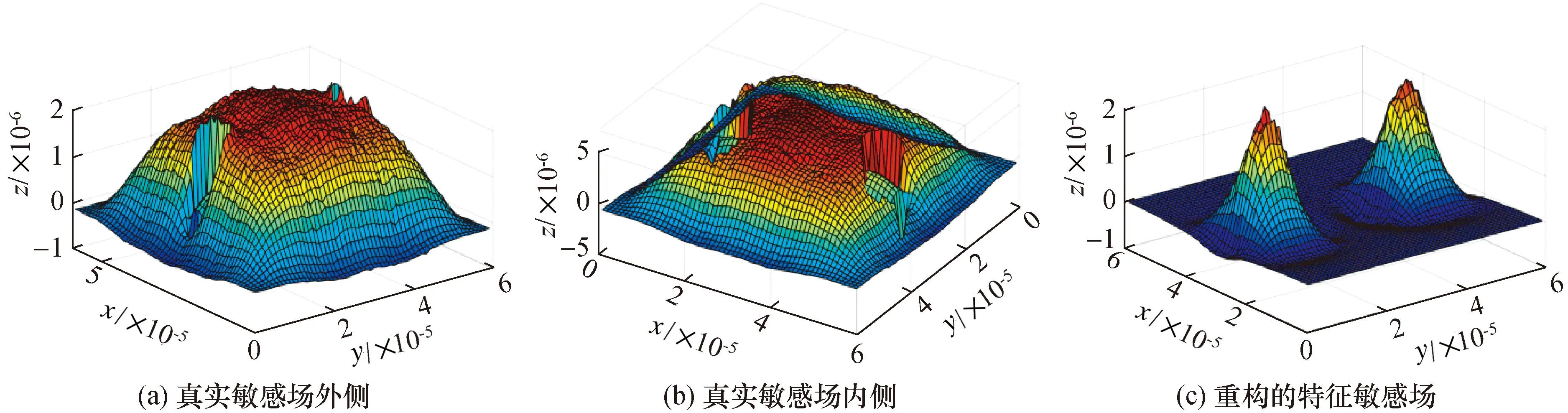
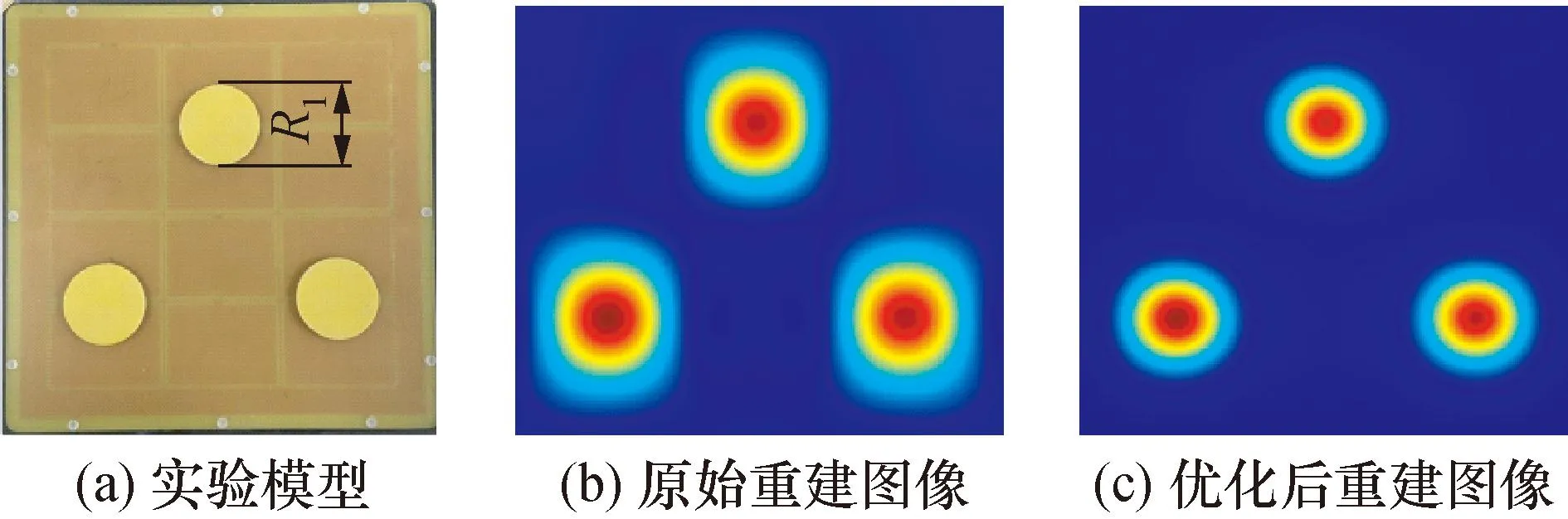
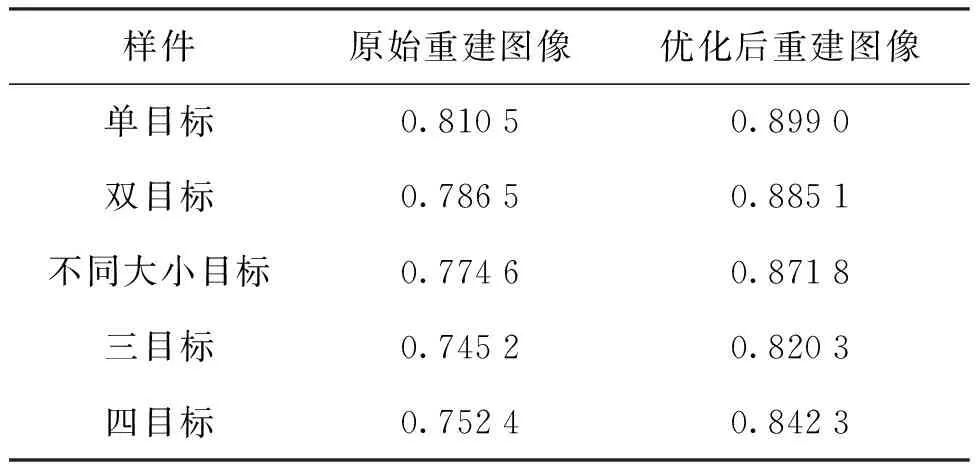
Sc=[Sis,…,Stj](1≤i (13) 图7(a)和图7(b)为图3中单目标检测模型的真实敏感场,图8(a)和图8(b)为图3中双目标检测模型的真实敏感场,它们在目标对象所在位置都具有一个向下凹陷的特征。图7(c)和图8(c)为空场敏感场自适应降维后的敏感场,从图中可以看到,特征敏感场只保留了空场敏感场的部分特征。在图7(c)和图8(c)中正好分别对应图3中单/双目标检测模型在中间存在向上凸起的特征,它们与检测模型真实敏感场的分布特征存在某种对应关系。因此在一定程度上,可以说敏感场通过自适应降维的方式能够匹配到真实敏感场的特征分布,从而实现与目标对象具有更强的关联性。 图7 单目标模型敏感场三维图Fig.7 Three dimensional map of sensitive field of single target model 图8 双目标模型敏感场三维图Fig.8 Three dimensional map of sensitive field of double object mode 敏感场灵敏度值的求解是依据有限元电势分布法,由式(4)可知,式中电场强度为矢量参数,因此在计算敏感场灵敏度值时会引入负灵敏度值。从图9(a)中子敏感场的三维网格图可以看到,由于负灵敏度值的存在,子敏感场特征区域的边缘会向下凹陷,导致子敏感场二维图中边缘会向外过度延展,甚至可能会出现局部分离区域,如图9(a)中二维等高线图所示。而图像重建又是通过敏感场区域投影的方式得到。因此敏感场特征边缘处严重的波动性会导致重建图像边缘模糊,进而影响重建图像的质量。 图9 子敏感场平方化前后的对比图Fig.9 Comparison diagram of the sub-sensitive field before and after squared 由于负灵敏度属于干扰数据,且数值在0值附近。为减弱负灵敏度值的影响,本文提出数据平方化的方式来对敏感场进行优化。从图9(b)中子敏感场的三维网格图可以看到,对敏感场数据采用平方优化的方式没有改变数据的分布特征,而且通过将特征边缘处的负灵敏度值改变为正灵敏度值减弱了特征部分边缘处的波动性。另外,子敏感场的特征部分被锐化,增强了特征部分与非特征部分的对比度,在重建图像时可以提高前景与背景的分离度,进而增强重建图像的质量。 将特征敏感场Sc平方化后的敏感场记为S*,如式(14)所示,敏感场优化后的图像重建算法公式变形为公式(15)所示: S*=(Sc)2=[Sis2,…,Stj2] (14) (15) 敏感场灵敏度值反映的是电容受介质分布变化的影响,灵敏度值平方化只是增强了数据间的相对差别,并没有改变其表征电容受介质分布的影响的作用。另外,由于本文电容参数选择的是电容变化量,因此式(15)中的灰度值矩阵G*反映的是介质分布的介电常数变化量。 同面阵列电容成像系统包括感应单元、数据采集单元和图像处理单元3个主要部分,另外,构成部分还有气浮台和位移台等。其中气浮台用于平稳测量平面,位移台用于移动检测。系统图示如图10所示。 图10 同面3×4阵列电容成像实验系统Fig.10 Coplanar 3×4 array Capacitive Imaging Experimental System 感应单元为同面3×4阵列电容传感器;数据采集单元为ITS-M3C高精度电容测量仪,设定传感器激励电压频率为1 MHz;图像处理单元为计算机软件,将采集到的电容数据,结合软件集成的LBP算法重建图像。本文采用离线重建的方式,将数据导出到本地,结合Tikhonov正则化法进行重建。 本文通过3种目标检测仿真模型对敏感场的数据特征进行了分析,并提出了数据降维并结合平方增敏的优化方法。本节将借助同面3×4电容成像实验系统对上述仿真过程进行实验还原,通过实验数据重建图像来验证所提优化方法的可靠性。以环氧树脂圆片来模拟种介质中由于出现异物或者缺陷所造成的电介质异常情况,对上述的方法进行验证。因此3种目标对象检测实验为:单目标、双目标和不同大小目标检测,如图11所示,其直径分别为R1=30 mm和R2=20 mm,厚度为2 mm。 图11 目标检测实验模型图Fig.11 Target detection experimental model diagram 图12为原始重建图像,图13为敏感场优化后的重建图像。每幅图像都包含3 600个像素点,其中背景区域的灰度值较低,呈蓝色;目标对象在重建图像中表现为灰度值较高的区域,且颜色越趋于红色灰度值越高。通过对比原始重建图像可以发现,目标对象边缘的波动性和不稳定性得到显著提高,如在目标对象的边缘能看出,明显深于背景颜色的部分消失。 图12 原始重建图像Fig.2 Original reconstructed image 图13 敏感场优化后的重建图像Fig.13 Reconstructed image after dimension reduction and sensitivity enhancement of sensitive field 在使用优化后的方法之后,降低了敏感场的非线性特性,使重建图像的目标对象从不规则的方形,变得接近于圆形,增强了特征物的轮廓清晰度,由此可以看出重建图像的质量得到了明显改善,使其更加接近于真实目标。在优化过程中,图像重建时间并不会有明显增加,单目标模型、双目标模型、不同大小目标模型的图像重建时间都保持在1 s左右。 另外,为防止实验的偶然性,还补充了两组不同于仿真模型的实验,分别为3个目标检测对象和4个目标检测对象的检测实验,如图14、图15所示。 图14 三目标检测实验结果图Fig.14 Experimental results’ diagram of three targets detection 图15 4目标检测实验结果图Fig.15 Experimental results’ diagram of four targets detection 在图14、图15中,图(a)为3目标与4目标的实验模型,图(b)为原始重建图像,图(c)为敏感场优化后的重建图像。从图14、图15来看,相较原始重建图像,敏感场优化后的重建图像具有更好的稳定性,降低了敏感场的非线性度,减弱了敏感场矢量求解造成4目标对象的边缘波动性,增强了目标对象的轮廓清晰度,图像质量得到了提高。 通过观察原始重建图像和优化后重建图像二者差异来判断算法的优劣并不直观,此处采用图像重建相关系数(correlation coefficient,CC),相关系数CC是衡量重建图像与原始图像相关性的一种度量。相关系数CC越接近数值1,代表其图像重建的质量越高,越接近于真实图像,评价公式为: (16) 对于5种样件,原始重建图像以及优化后重建图像的相关系数如表1所示,优化后重建图像相较于原始重建图像的相关系数有较大程度的提升。在相关系数方面,优化后成像效果提升均在10%以上,其中提升效果最差的是三目标,最好的是双目标和不同大小目标。对比图12(c)与图13(c)可以发现,重建图像的目标对象从不规则的方形,变得接近于圆形,而且小的目标对象在采用了优化方法之后,重建图形更加接近目标对象,这一点从相关系数上也得到了证明。结合图12~图15以及表1可以分析出,在采用了本文提出的数据降维并结合平方增敏的优化算法情况下,重建图像的效果更加接近于实际情况,要明显好于原始重建图像的结果。 表1 图像相关系数CCTab.1 Image correlation coefficient CC 本文针对同面3×4阵列电容传感器敏感场非线性特性导致重建过程存在严重不适定性的问题,提出了一种敏感场的数据降维、平方增敏的优化方法。其中降维方法是基于最大熵原理,依据特征电容数据作为索引实现了敏感场数据的自适应降维,降维后得到的敏感场具有更高的特征匹配度。另外,针对敏感场负灵敏度值的问题,通过平方化的处理方法,不仅改善了负灵敏度值的影响,还降低了特征物边缘的波动性,增强了特征物的轮廓清晰度。最后设计了多组检测实验,发现采用优化后的重建图像能够减弱了目标对象的边缘波动性,并降低了敏感场的非线性度,提高了重建图像的质量与稳定性,验证了本文方法的有效性。下一步工作是探讨成像分辨力与优化算法之间是否存在影响等方面。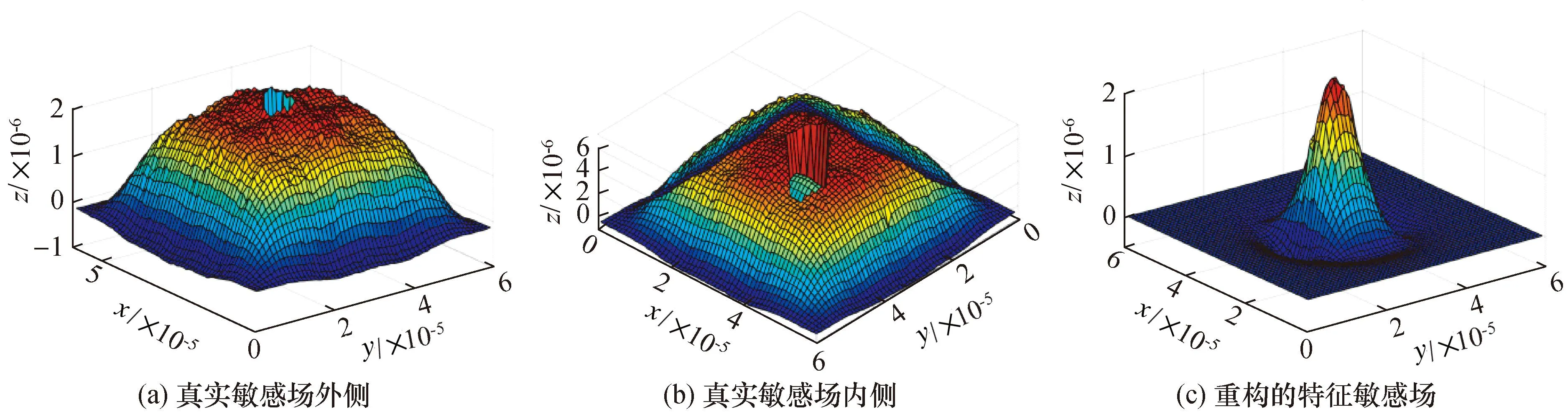
3.2 基于平方化的敏感场增敏方法

(1≤i
4 实验验证与结果分析
4.1 实验系统与实验流程

4.2 实验结果分析


4.3 图像质量评价
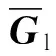
5 结 论
