基于发射率修正模型的红外测温补偿方法

米松涛, 张玉存, 付献斌, 颜 方, 孔 涛

(1.燕山大学，河北 秦皇岛 066300； 2. 河北环境工程学院，河北 秦皇岛 066300)

1 引 言

红外测温是一种广泛应用的非接触测温方法。相比其他测温方法,红外测温有非接触、非侵入、实时在线、无有害辐射、提供二维温度分布等优点[1]。然而,红外测温在工业应用过程中,测量结果容易受到多种因素的影响,如设备自身因素[2]、测量角度[3]、测量距离[4]、周围环境[5]、表面发射率[6]、被测物温度[7]等。针对这些影响因素,国内外学者进行了大量研究,推动了红外测温的发展。

在工业应用红外测温时,被测物体的表面粗糙度是影响红外测温精度的主要因素[8]。表面粗糙度影响红外测温精度的研究包括理论和实验两方面。

在理论研究方面,Ke W等[9]基于几何光学(geometrical optics,GO)分析了物体表面入射角、均方根偏差与相关长度的比值、均方根偏差与波长的比值对红外发射率的影响;Dai S S等[10]构造2个端元的线性最小二乘光谱反卷积红外发射率模型,提高了对表面约束条件差的目标的红外发射率测量精度;Berger J A等[11]基于时域有限差分Maxwell解算器模拟,分析了表面高度和坡度的粗糙度组合参数与红外发射率变化相关性。这类方法研究了粗糙表面的局部特征参数对红外发射率的影响,但对完整粗糙表面的红外发射率仍有不足。针对几何近似法中对粗糙纹理表面整体特征参数分析不足,Sta B等[12]基于Agababov粗糙函数建立了简单粗糙因子与铝表面光谱发射率分析模型;Jo H等[13]基于基尔霍夫定律计算模型,对多重叠加余弦函数傅里叶级数的粗糙表面发射率分析;Xu Y等[14]基于阿加巴波夫粗糙度函数改进的发射率模型,以推断具有不同表面粗糙度的样品发射率。Agababov粗糙度函数和多重余弦傅里叶级数表示的粗糙表面与实际粗糙表面仍有很大差距,对实际粗糙表面的红外发射率分析仍有不足。

在实验研究方面,Wen C D等[15]分析线性发射率模型(LEM)和对数线性红外发射率模型(LLE)在测量表面温度的准确性,得到三阶LEM模型对不同合金表面粗糙度的发射率拟合精度高;Sopori B L等[16]提出一种计算具有平面和非平面表面形态的硅晶片的红外发射率方法,并通过实际案例证明该方法的有效性;Koch M等[17]分别采用短波和长波红外光谱测量了不同湿度和粗糙度的土壤反射情况,建立了表面粗糙度与土壤反射率和光谱特征模型;Seifter A等[18]比较了激光偏振法和积分球反射法对粗糙金属表面的红外发射率测量,对比分析了激光偏振法在测量粗糙表面发射率的局限性;Wen C D等[19]通过实验对抛光和粗糙铝合金表面的发射率特性进行研究,提出基于多光谱辐射测温模型计算铝合金发射率,并确定发射率模型的经验常数。这些实验研究对材料和环境有一定依赖性,红外发射率模型在实际生产加工过程中应用仍有不足。

红外测温技术作为一种非接触测温方法,在材料研制与热加工过程中有广泛应用。然而,当测量对象表面粗糙度较大时,传统红外测温方法无法有效补偿表面发射率的变化,导致测温精度下降,影响其工业应用。本研究考虑到表面粗糙度会导致多个空间尺度上的发射率不均匀变化,从粗糙表面整体特征出发,提出一种双尺度发射率修正的红外测温补偿方法。该方法用于补偿搅拌摩擦焊焊缝红外测温过程中表面粗糙度对测温精度的影响。

2 红外测温补偿方法

2.1 红外测温原理

根据红外热像仪的基本测温原理,被测物体表面真实温度为:

(1)

式中:T0为被测物体表面真实温度;ε为物体发射率;τa为大气透射率;εa为大气辐射率;TB为被测物体表面温度;Tu为环境温度;Ta为大气温度;n=3.988 9。

由式(1)可以看出,红外测温的精度主要取决于被测物体表面发射率。因此,为提高红外测温精度,需要对表面发射率进行准确测量。

2.2 双尺度粗糙表面

为确定表面粗糙度与表面发射率的关系,本文对粗糙表面建立双尺度粗糙表面模型。基于蒙特卡罗法和分形理论建立随机粗糙表面,其中基于蒙特卡罗法表示的表面功率谱密度函数负幂律部分为

(2)

式中:Xm,Yn为(m,n)处的离散采样点;Lx,Ly分别为粗糙表面长度和宽度;kx,ky分别为x和y方向的离散波数;kmk,knk为(m,n)处离散傅里叶的频率项;i为粗糙表面(m,n)处离散点的高度;M和N分别为等距离散点的个数。。

分形理论构建表面的功率谱密度函数正幂律部分为:

(3)

式中:D为分形维数;G为特征尺度系数;L为表面的样本长度;φ为随机相位函数;γn表示轮廓的空间频率,n是>1的常数,通常取1.5,γ为正幂律因子。

则各向异性粗糙表面的功率谱密度函数为

ZR=ZR1+ZR2

(4)

对于零件表面,通常具有一定的纹理轮廓,可以用等式(1)表示

ZW(x,y)=f(x,y)

(5)

对粗糙表面和纹理表面分别进行Z-score标准化,粗糙纹理表面可转化为:

(6)

则最终合成的粗糙纹理表面为ZD,其均值为μD,标准差为δD:

ZD=(ZX-μX+μD)δD/δX

(7)

式中:μX、δX分别为ZX的均值和标准差。

该方法采用叠加多组相互独立的正弦信号来描述最终的粗糙表面。各个正弦信号表示不同尺度下的表面起伏,其和表示了多尺度效应下的总体表面形貌,其均值表示表面高低变化的中心位置,其标准差表示表面高低变化的整体幅度,刻画了表面粗糙度。

2.3 红外温度补偿

本文以正弦纹理构成的粗糙纹理表面为例,建立散射分析计算模型,研究发射率与表面粗糙度的联系。双尺度粗糙表面的散射如图1所示。

图1 双尺度粗糙表面的散射示意图Fig.1 The scattering diagram of rough textured surface

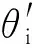
本地坐标系单位坐标的单位矢量可定义为

(8)

则纹理粗糙表面单位矢量为

(9)

式中:fx和fy分别表示粗糙纹理表面沿x和y方向的导数。

由式(8)和式(9)可以得出本地单位坐标的单位矢量为

(10)

其中,

当粗糙纹理表面ZD上一点斜率为零时,主坐标系与本地坐标系一致,此时,定义水平极化矢量h,h′和垂直极化矢量v,v′分别为

(11)

由于粗糙纹理表面ZD由ZR和ZW耦合形成,根据散射系数的定义,纹理粗糙表面的极化方向散射系数可以表示为:

(12)

(13)

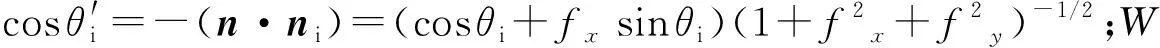
同样可以得出:

(14)

对纹理表面散射系数进行集平均可以得到:

(15)

式中:Pθi(fx,fy)代表θi方向观察的纹理表面的斜率概率密度函数;P(fx,fy)为粗糙纹理表面斜率fx和fy的概率密度函数。

由式(11)和式(13)可以得出散射近似解可以表示为

(16)

(17)

(18)

对粗糙纹理表面某一点的散射系数在表面ZD上积分可以得到粗糙纹理表面整体的散射系数:

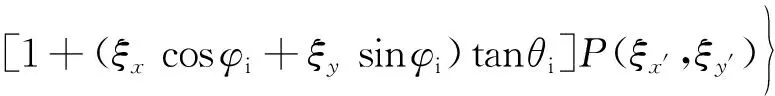
(19)

对粗糙纹理表面的散射系数在(0,4π)内积分可得粗糙纹理表面ZD的反射率γpp为:

(20)

根据式(20)和基尔霍夫定律可以得出粗糙纹理表面的发射率模型:

ε=α=1-ρ-γ

式中:ε为材料表面发射率;α为材料的吸收率;ρ为材料透射率;r为材料反射率。

将修正后的表面发射率代入式(1)可以得到本文的红外补偿算法。

3 实验研究

搅拌摩擦焊是一种环保的固态焊接技术。如图2 所示,其焊接过程较为复杂,涉及材料的高速流动、变形与塑性行为,使得焊缝表面形貌处于持续演化之中。焊接参数和工艺的变化会引起焊缝表面形貌的相应改变,为焊缝温度测量带来挑战。

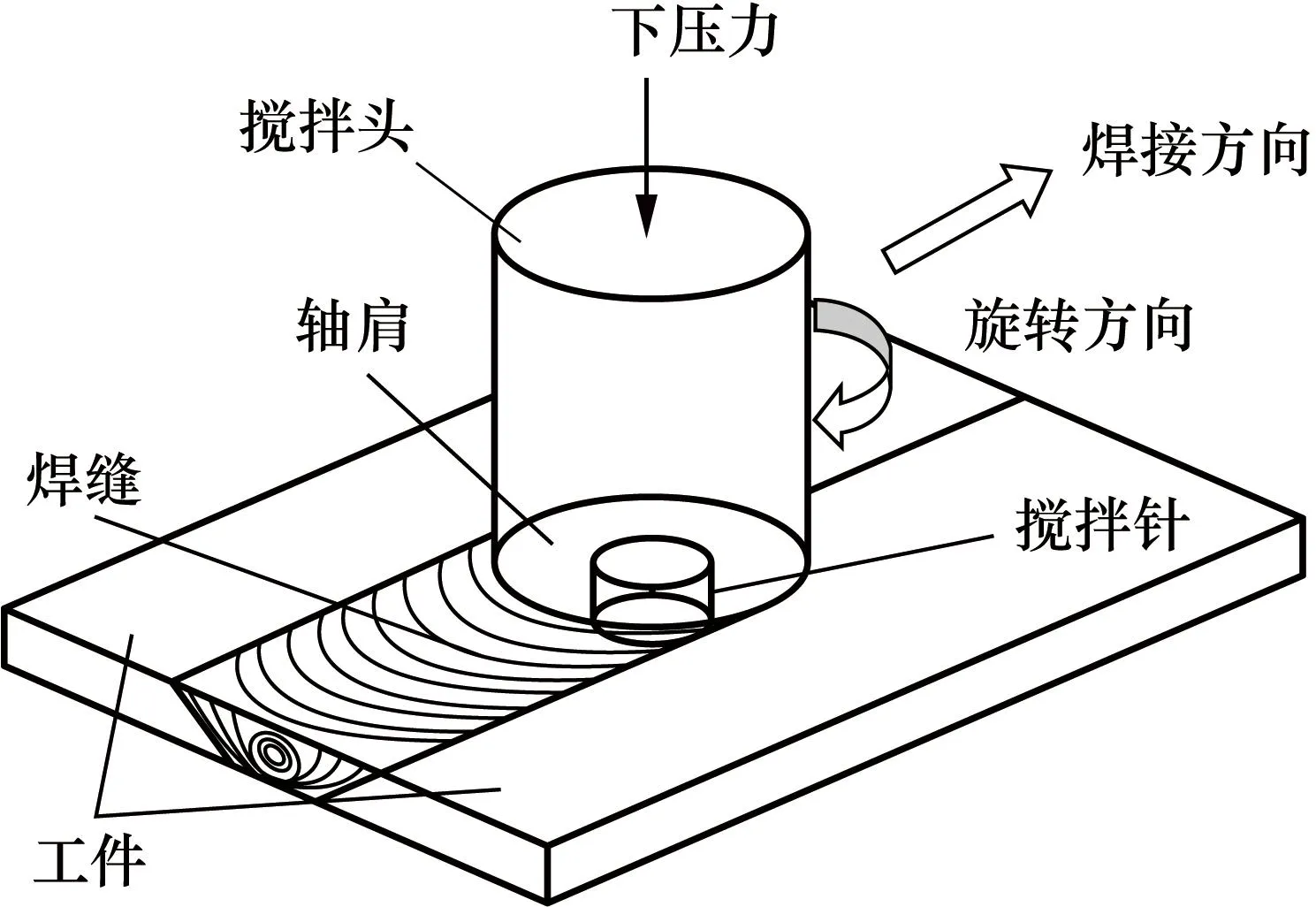
图2 搅拌摩擦焊焊接原理示意图Fig.2 Schematic diagram of FSW

为验证本文提出的红外测温补偿算法有效性,将该算法应用于搅拌摩擦焊[20]焊接过程红外测温系统。根据实际焊接过程和本文提出粗糙纹理表面的红外补偿算法,建立焊缝表面粗糙纹理表面的模型;将校正后的红外发射率应用于红外测温系统,通过红外测温数据对比分析,验证了本文红外测温补偿算法的有效性。

首先,对焊缝表面进行功率谱分析,如图3所示,焊缝表面纹理形状为类洋葱纹,根据式(7)建立焊缝表面粗糙度模型;然后,由式(20)可以得到焊缝表面红外发射率模型;最后,将本文的红外测温补偿方法应用于铝合金搅拌摩擦焊红外测温系统,验证其有效性。

图3 焊缝表面示意图Fig.3 Surface sketch and 3D model of friction stir welding

图4为本文进行的焊接实验。实验平台型号为FSW LM BM16。红外测温设备型号为VarioCAM 680,分辨率640×480,温度范围为-40～1 200 ℃。标准接触式热电偶为Jt-31精密数字温度计K型热电偶,测温范围为0～650 ℃,分辨率为0.02 ℃。实验工件为8 mm厚2A14铝合金板材,焊接方式为直缝焊接。焊接参数:焊接速度为150 mm/min,主轴转速为500 r/min。

图4 搅拌摩擦焊焊接过程Fig.4 Friction stir welding process and infrared temperature measurement diagram

焊接实验过程中,分别使用接触式温度计和红外热像仪对焊缝表面温度进行测量,红外测温系统初始测量值和修正后的测温值如表1所示。表中,T0为标准热电偶测量值,T1为红外测温系统初始测量值,T2为应用红外测温补偿方法的测量值。由表1可以计算得到,初始红外测温系统测量值与标准热电偶测量值平均误差为1.638 ℃,最大误差为2.686 ℃。红外测温补偿方法测量值与标准热电偶测量值平均误差为0.649 ℃,最大误差为1.058 ℃。

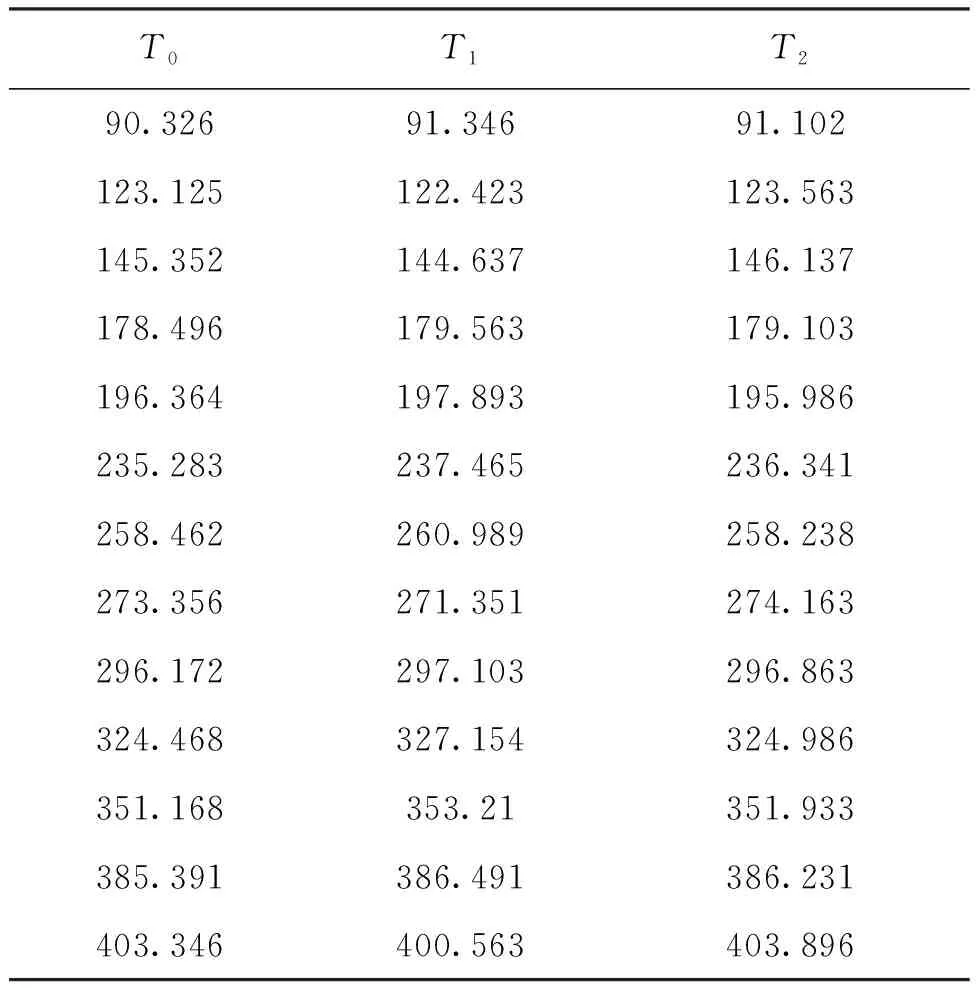
表1 搅拌摩擦焊焊接过程温度数据Tab.1 Measurement value of infrared temperature measurement system before and after correction ℃

图5为采用本文算法补偿前后测温误差曲线图,Δ1为初始红外系统温度值与标准热电偶温度值的差值,Δ2为应用本文红外测温补偿方法测量值与标准热电偶测量值的差值。由图5可知,红外测温系统的最大测量误差由补偿前的2.783 ℃减小到1.058 ℃,平均测量误差由校正前的1.638 ℃减小到校正后的 0.649 ℃。本文提出的红外测温补偿算法在焊缝表面温度测量中,测量误差控制在1%以内。

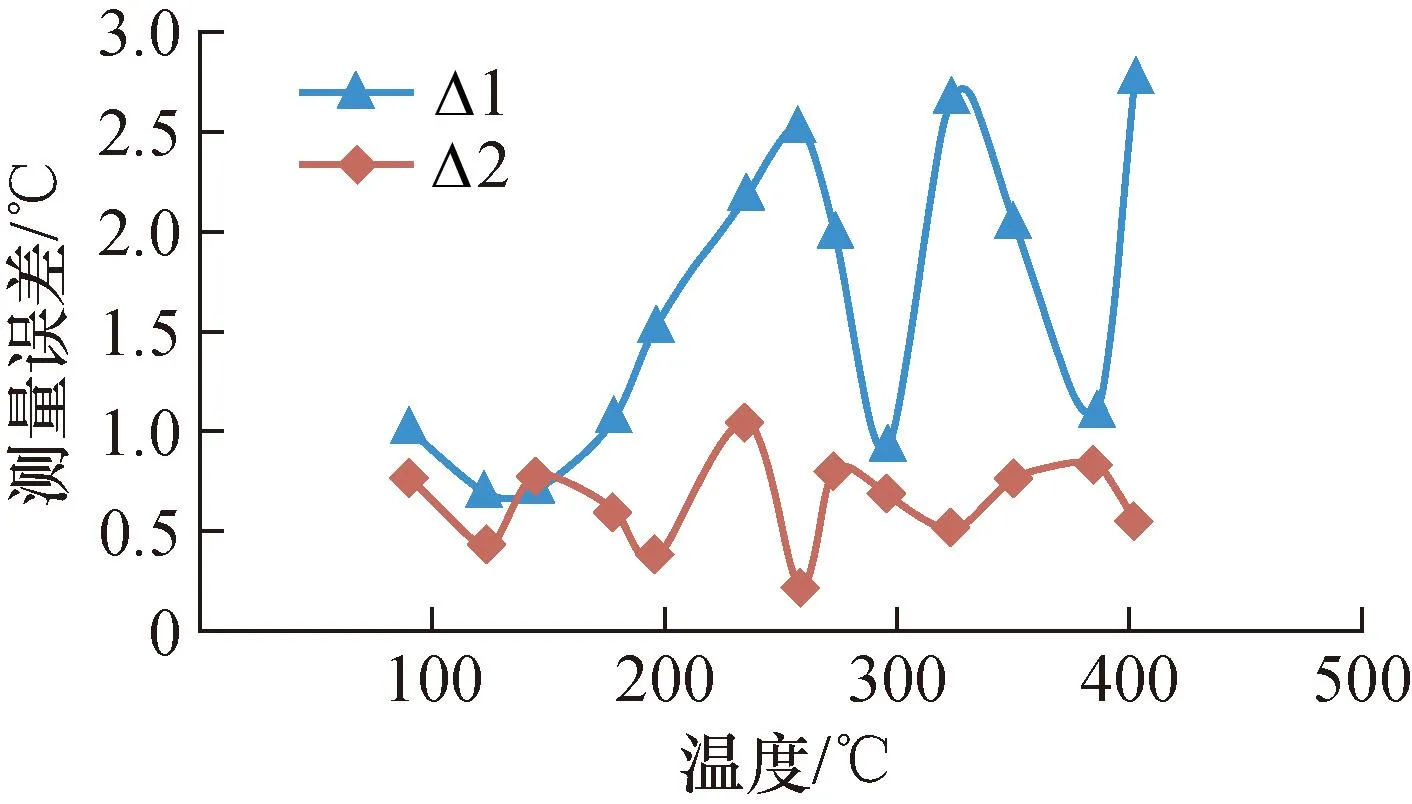
图5 红外测温算法补偿前后误差曲线Fig.5 The measurement error curve of infrared measurement system before and after correction

4 结 论

本文通过分析表面粗糙度对表面红外发射率的影响,提出了一种基于发射率修正模型的红外测温补偿方法。该方法基于双尺度粗糙表面建立了粗糙表面发射率校正模型,实现了红外测温补偿方法中表面发射率校正。通过搅拌摩擦焊焊缝红外测温实验对比了采用补偿算法前后测量结果,红外测温系统的最大测量误差由补偿前的2.783 ℃减小到1.058 ℃,平均测量误差由补偿前的1.638 ℃减小到0.649 ℃。

结果表明,本文提出的红外补偿算法减少了测量过程中表面粗糙度对红外测温的影响,进而提高了红外测温的精度。该算法为工业化红外测温提供了一种有效的解决方法,可以用于各种红外测温场合以提高测温精度和可靠性。