人工采砂坑对规则波岸礁水动力特性的影响研究

王旭，屈科，2，3，门佳

（1.长沙理工大学 水利与环境工程学院，湖南 长沙 410114；2.洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙 410114；3.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114）

在全球气候变化和海平面持续上升的背景下，地处热带和亚热带地区的珊瑚海岸，特别是地势较低的环礁岛屿，极易受到飓风和海啸所引起的极端波浪的影响。典型的珊瑚礁地形主要包括陡峭的礁前斜坡和相对平坦的礁坪[1-2]。以往的研究结果表明，大部分的入射波能可以通过礁缘或礁冠附近的波浪破碎以及礁坪底部的摩擦被耗散掉[3-6]，因此珊瑚礁对极端波浪具有天然的缓冲作用，可以有效地保护礁后人口密集城镇的安全[7-8]。近些年来，为促进地区的经济发展，环礁群岛国家计划修建众多的公路、港口、机场和其他基础设施（如马绍尔群岛）[9]，这些基础设施的建设需要大量的建筑原材料[10]。为满足基础设施建设的需要，在礁坪上进行挖掘逐渐成为建筑材料的主要来源。传统沙质海岸的疏浚可以逐步适应海岸地貌及水动力的变化，而礁坪上的采掘通常会对珊瑚礁的海岸环境带来永久性的影响[11]。礁坪上的人工采掘不仅会对珊瑚群落的生态平衡产生深远影响，更会在一定程度上影响珊瑚礁的波浪水动力特性[12]。因此，系统开展人工采砂坑对珊瑚礁海岸波浪水动力特性影响的研究工作具有重要的科学意义和工程应用价值。

近几十年来，国内外的学者对波浪在珊瑚礁上传播演变规律开展了大量的研究工作，Kench等进行了大量的现场勘测[13-15]，Gourlay 等进行了相关的理论分析[16-17]；Liu等开展了许多实验研究，研究各种波浪与珊瑚礁之间复杂的水动力特性[18-21]；许多学者通过数值模拟的方法研究了珊瑚礁与各种波浪之间的复杂相互作用（规则波[22-23]、非规则波[24-26]、海啸波[27]和畸形波[28]）。这些研究的主要内容是波浪在不同珊瑚礁上传播过程中发生的波浪破碎和波浪的增水效应[29-30]、低频长波的变化规律[31-32]，以及波能的耗散。虽然这些研究对于正确理解不同波浪作用下珊瑚礁水动力特性具有重要意义，但对人为活动影响下采砂坑的研究还远远不够[33]。近年来，少数学者通过现场观测、物理模型试验、数值模拟等方面对存在采砂坑的沿礁波浪特性进行了研究。Ford等[9-10]通过对马绍尔群岛Majuro 环礁进行的实地观测，研究了波浪在有采砂坑和无采砂坑的礁坪上传播变形与破碎的过程，研究结果表明，采砂坑的存在对低频长波的影响较大，导致有采砂坑附近的海岸线附近波高减小；Yao等[34]]和旷敏等[35]利用波浪水槽进行了物理模型试验，分别研究了采砂坑的宽度，采砂坑的位置变化对短波波高，低频长波和波浪增水的影响，并分析了采砂坑的宽度，采砂坑的位置变化对礁坪上低频长波的形成及其共振机理的影响；Klaver 等运用XBeach 非静压模块数值模拟了采砂坑的宽度和位置的变化对局部波高及波浪爬高的影响[11-12]；张善举[36]对非静压模型NHWAVE、FUNWAVE-TVD、Coulwave 等3 个波浪数值模型进行了对比分析，发现NHWAVE 能准确地模拟不同破碎波类型波浪在珊瑚礁礁坪上的波浪增减水，并且计算效率最快。因此本文选用NHWAVE来数值计算。

然而，目前国内外尚未有学者研究人工采砂坑对规则波岸礁水动力特性影响。因此，为了补充以往学者在人工采砂坑岸礁波浪传播演变特性的研究工作，本研究基于非静压单相流模型（NHWAVE），系统研究人工采砂坑对珊瑚礁坪上规则波的传播变形和爬高的影响。详细讨论了入射波高、礁坪水深、波浪周期、采砂坑宽度和采砂坑深度，以及采砂坑的位置等几个主要因素的影响。

1 数值模型

1.1 控制方程

NHWAVE 是Ma 等[37]开发的非静压波浪数值模型。此模型以守恒形式的不可压的Navier-stoke方程作为控制方程，为了精确表达水底和自由表面的形状，Ma 采用了σ 坐标系对控制方程进行转换，表达式中：D 为x、y、t的函数，h 是静止水深，η为自由液面高程。

1.2 湍流模型

本文采用标准的k-ε 湍流模型来计算湍流黏性系数，其控制方程如下所示：

1.3 离散格式

应用有限体积∕有限差分组合法求解了NHWAVE 的控制方程。动量方程中的通量项用激波捕获的HLL-TVD 格式离散化。应用二阶混合线性∕抛物线近似（HLPA）方案离散了k-ε湍流模型控制方程中的对流通量项。采用二级二阶非线性强稳定性保持（SSP）Runge-Kutta 方案进行时间行进，获得二阶时间精度。计算时间步采用自适应时间步长，将CFL 数设为0.25，以满足数值稳定性的要求。关于数值计算模型NHWAVE 算法的详细描述可参考文献[39]。

2 模型验证

2.1 波浪在岛礁地形上传播演变的验证

实验数据采用Yao 等[40]在南洋理工大学水动力实验室进行的岸礁地形下规则波增减水的物理实验。二维数值波浪水槽计算域与实验保持一致，如图1 所示。数值计算域为36 m，左侧为造波边界，岸礁模型礁前斜坡坡度为1∶6，礁前斜坡坡脚离造波区21 m，斜坡长度b = 2.1 m，礁坪长度L3= 8.9 m，模型高度为0.35 m，沿程布置12 个测点，水槽右侧设置海绵消波层。x 方向为规则波传播方向，网格大小dx= 0.02 m；z 方向为水深方向，共划分20层网格。数值模型验证工况如表1所示。波高仪放置的位置与实验相同，表2给出了验证工况波高仪的确切位置（以斜坡坡脚为参考点）。

表1 验证工况

表2 实验的波规（G1-G12）距斜坡坡脚的距离 单位：m

图1 计算区域布置

图2－图5 展示了数值模拟结果与实验值的对比。为了更为直观地判断数值模型的计算精度，本文引用Warner 等[41]建议的skill 数，skill 数的定义采用Wilmott[42]的方法，式（8）中：Xmodel和Xobs分别表示数值计算值和实验观测值，上划线表示取平均值，skill数越接近于1表示模型计算精度越高，skill数越接近于0表示模型计算精度越低。

图2 case1不同位置表面高程的时间序列

图3 case1沿礁平均波高和平均水位对比图

图4 case2不同位置表面高程的时间序列

图5 case2沿礁平均波高和平均水位对比图

通过对比可以看出：计算结果与实验数据的吻合度较高。Case1 中G5 和G7 处的波面计算值要大于实测值，以及平均水位计算值略大于实测值这和Yao 等[40]采用一维Boussinesq 模型计算的结果相近，其给出的解释是，这个误差可能是由于破碎带内夹带的气泡造成的。所以该模型有能力模拟规则波与岛礁地形的复杂水动力过程。

2.2 波浪在采砂坑岸礁地形上传播演变的验证

本节数值计算了非规则波浪在岛礁地形上传播演变的水动力学过程，将计算结果与Yao 等[34]的实验结果进行对比，验证非静压模型NHWAVE计算波浪在采砂坑岸礁上传播变形的能力。二维数值波浪水槽计算域与实验保持一致，如图6 所示。数值计算域为36 m，左侧为造波边界，岸礁模型礁前斜坡坡度为1∶6，礁前斜坡坡脚离造波区27.3 m，斜坡长度为2.1 m，礁坪长度为3.6 m，模型高度为0.35 m，采砂坑位于礁坪中间处，采砂坑宽度Wp= 0.80m，采砂坑深度为0.20 m，沿程布置18 个测点，水槽右侧设置海绵消波层。x方向为规则波传播方向，网格大小dx= 0.02 m；z方向为水深方向，共划分20 层网格。数值模型验证工况有效波高Hs= 0.08m、谱峰周期Tp= 1.5s、礁坪水深hr= 0.05m。波高仪放置的位置与实验相同。图7 展示了数值模拟结果与实验值的对比。通过对比可以看出：计算结果与实验数据的吻合较好。所以该模型有能力模拟波浪在采砂坑岸礁地形上传播演变，可进一步研究规则波在带有人工采砂坑岸礁上的传播演变。

图6 计算区域布置

图7 低频长波波高、短波波高、平均水位的空间分布

3 工况设置

本文数值研究了人工采砂坑对规则波在岸礁地形上传播变形和爬高过程的影响。系统研究了入射波高H、礁坪水深hr、波浪周期T、采砂坑中心位置xp、采砂坑深度Hp、采砂坑宽度Wp等因素的影响，布置如图8 所示。岸礁模型参考Yao 等[40]的物理模型试验，礁前斜坡坡脚位于造波区下游21.0 m 处，珊瑚礁坪的高度为0.35 m。采砂坑的尺寸根据Ford 等[10，34]对马绍尔群岛某地开展的原型观测作为参考依据，并采用弗劳德相似定律以1∶20 的几何比尺构建。对于标准工况，采砂坑中心位置xp= 25.6 m，采砂坑深度Hp= 0.2 m，采砂坑宽度Wp= 0.8 m，dw= 0.08 m，礁坪长度Lp=5.0 m，礁前斜坡tan α =1∶6，礁后斜坡tan β = 1∶12，沿计算域布置90 个波高仪，记录水面高程和波浪上升高度的时间演变，如图8 所示。x 方向为规则波传播方向，网格大小dx= 0.02 m；z 方向为水深方向，共划分20 层网格。无采砂坑的计算区域为在采砂坑的基础上Hp= 0.0 m。详细的工况设置参照表3，共38个工况。

表3 数值模拟工况设置表

图8 带有采砂坑的珊瑚礁的计算布置

4 数值分析与讨论

4.1 水动力分析

本节对规则波在有无采砂坑的岸礁上传播的水动力过程展开分析。对于无采砂坑的岸礁采用A3工况，有采砂坑的岸礁采用B3工况。图9 为具有代表性时刻的水体速度云图，由图可知，当波浪传播至采砂坑附近时，采砂坑的存在对其周围的流场影响相对较大（图9（c）、图9（g）），但对距离采砂坑较远处的流场几乎无影响。且由图9（g）、图9（h）可以观察到规则波与采砂坑之间复杂的相互作用现象，即当波浪传播至采砂坑时，高速运动的波浪与采砂坑中静止的水体之间发生强烈的质量和动量交换（波浪运动的能量一部分向前继续传播、一部分流向采砂坑内，采砂坑中部分水体也会向上涌出），使得波浪在采砂坑上向岸继续传播的速度减小。图10 为具有代表性测点的自由液面高程的时间序列，由图可知，当规则波在采砂坑之前的位置传播时（x = 20.0 m、x = 21.0 m、x = 22.6 m、x = 23.1 m），测点处的自由液面的时间演变受采砂坑存在的影响较小；然而，采砂坑之前（x = 25.2 m）的局部波高会由于坑壁的反射和水体的阻碍相对增加；采砂坑里（x = 25.6 m、x = 25.9 m）的测点自由液面最大高程相对减小，采砂坑中心处的自由液面最大高程减少了26.76%，采砂坑末端减少了13.7%，采砂坑中心处的自由液面最大高程减少得相对较多；采砂坑的存在对岸线附近（x = 28.1 m）自由液面的影响较小。由（x = 25.2 m、x = 25.6 m、x = 25.9 m、x =28.1 m）处的自由液面的时间序列图可知，由于采砂坑的存在，会阻碍涌浪向岸的传播。图11（a）为有无人工采砂坑时岸礁上局部波高的空间分布对比图，从图可以看出，采砂坑的存在分别升高和降低了坑前和坑内的波高，这分别是由坑内水柱的能量守恒和坑壁的反射造成的，但对岸线附近的波高影响较小。图11（b）展示了有无人工采砂坑时局部平均水位的空间分布对比图，由图可知，波浪在礁前斜坡爬坡过程中产生减水效应（MWL ＜0），随后波浪破碎MWL 显著增大，转变为增水（MWL ＞0），并在岸线附近达到最大，定义在礁坪上的最大平均水位为波浪增水值（ηr），采砂坑的存在对礁坪上的平均水位几乎没有影响，这主要是因为波浪的破碎主要发生在礁前斜坡附近，位于礁坪中央的采砂坑对波浪的破碎的影响已不再显著。图12（a）、12（b）分别是最大水深平均速度的空间分布对比图和波浪爬高时间序列的对比图，由图12（a）可知采砂坑的存在降低了坑内的水深平均速度，由于坑内壁的反射使得礁缘处的最大水深平均速度增大，但降低了在岸线附近的水体速度，这点结合图9 也可知；图12（b）表明了采砂坑对礁后斜坡上的最大爬高有显著影响，这可能是因为采砂坑的存在降低了在岸线附近的水体速度，因此降低了涌浪的最大爬高（最大爬高为：在波浪传播稳定后20 个波浪周期内，每个周期内最大爬高值相加的平均值）。

图9 不同时间情况下水体的速度云图

图10 不同测点处自由液面高程的时间序列对比图

图11 局部波高与平均水位的空间分布对比图

图12 最大水深平均速度的空间分布与爬高的时间演化对比图

4.2 入射波高的影响

本节通过计算A1、A2、A3、A4、A5，B1、B2、B3、B4、B5这10 个工况，研究了不同入射波高度下采砂坑的存在对规则波传播演变水动力特性和爬高过程的影响。图13 展示了不同入射波高条件下局部波高沿计算域的空间分布，结果表明：当波高增大时，波浪开始的破碎位置会略微提前，但采砂坑的存在对波浪破碎位置仍没有影响；随着入射波高的逐渐增加，采砂坑后一定区域内局部波高降低的范围无明显变化，局部波高最大降低幅度减小，对于入射波高Hs/h=0.10 时最大降低幅度为27.2%，Hs/h= 0.30 时降低幅度为20.9%。图14 为有无采砂坑波浪增水随入射波高变化对比图，由图可知，随着入射波高的增大，波浪的破碎程度也增大，波浪破碎带的辐射应力梯度增加，因此波浪增水也会显著增加，但礁坪上的波浪增水并没有因采砂坑的存在而明显改变。图15 展示了有无采砂坑的情况下反射系数随入射波高的变化，当入射波高增大时波浪的反射系数也会增大，采砂坑的存在虽然对礁前斜坡之前的流动过程和流场影响很小，但会增加波浪的反射系数。图16 为规则波的最大爬坡高度随入射波高的变化对比图，由图可以看出，岸线附近规则波的最大爬升高度随入射波高单调增加，由于采砂坑内复杂的流场结构会消散更多的动能，使岸线附近的流速较弱，因此有采砂坑的岸礁最大波浪上升高度低于没有采砂坑的岸礁，平均低11.7%。

图13 不同波高作用下局部波高的空间分布

图14 波浪增水随入射波高的变化

图15 反射系数随波高的变化

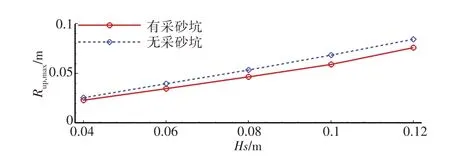
图16 规则波的最大平均爬高随波高的变化

4.3 礁坪水深的影响

为研究在不同礁坪水深下采砂坑的存在对规则波传播演变和爬高过程的影响，计算并分析了C1、C2、A3、C3、C4，D1、D2、B3、D3、D4这10 个工况。图17 展示了不同礁坪水深条件下局部波高沿计算域的空间分布，结果表明：当礁坪水深增大时，波浪开始的破碎位置会略微往后，但采砂坑的存在对波浪破碎位置没有影响；随着礁坪水深的逐渐增加，采砂坑前局部波高升高的范围增大；采砂坑后一定区域内局部波高降低的范围和最大降低幅度均随之增大，当hr= 0.10 m 时最大降低幅度为20.6%，而hr= 0.0 m 时降低幅度仅为2.6%。从图18可知，波浪增水随礁坪水深的增大单调递减，这是因为水深的增大减弱了波浪破碎带的辐射应力梯度，礁坪上的波浪增水因采砂坑的存在而略微降低，这种影响在水深较小时更为明显，这可能是因为在不同的礁坪水深条件下破碎带的宽度不同造成的。图19 展示了有无采砂坑的情况下反射系数随礁坪水深的变化，当礁坪水深增大时波浪的反射系数减小，当hr≥0.025 m 以后采砂坑的存在会增加波浪的反射系数。由图20 最大爬高随礁坪水深的增大单调递减，这可能是因为水深的增加减弱了涌浪在礁坪上的水体流速；同时岸线附近规则波的最大爬高始终低于没有采砂坑的，平均低8.6%。

图17 不同礁坪水深条件下局部波高的空间分布

图18 波浪增水随礁坪水深的变化

图19 反射系数随礁坪水深的变化

图20 规则波的最大平均爬高随礁坪水深的变化

4.4 波浪周期的影响

本节通过计 算E1、E2、A3、E3、E4，F1、F2、B3、F3、F4这10 个工况，研究了不同波浪周期下采砂坑的存在对规则波传播演变水动力特性和爬高过程的影响。图21 展示了不同周期条件下局部波高的空间分布，结果表明：波浪周期的增大对波浪开始的破碎位置不产生影响，但增大了波浪在礁前的浅水效应，使临界破碎波高增大，并且增加了礁坪上的破碎带宽度；随着波浪周期的逐渐增加，采砂坑前局部波高升高的范围增大及采砂坑后一定区域内局部波高降低的范围均增大，且坑内局部波高最大降低幅度也随之增大，当T=2.0 s 时最大降低幅度为28.76%，T= 1.0 s 时降低幅度为15.1%。由图22 可知，波浪增水随波浪周期的增大单调递增，这可能是因为当波浪周期增大时波能流也随之增大，采砂坑的存在减弱了在礁坪上的波浪增水效应，在大周期的情况下最为明显。图23 展示了有无采砂坑的情况下反射系数随波浪周期的变化，当周期增大时波浪的反射系数先增大后减小。由图24 可以看出，波浪最大爬高随波浪周期的增大单调递增，这可能是因为当周期增大时，波浪的破碎程度降低，增加了波浪在礁坪上的透射能力；由于采砂坑的存在岸线附近规则波的最大爬升高度始终低于没有采砂坑的最大爬升高度，平均低9.625%。

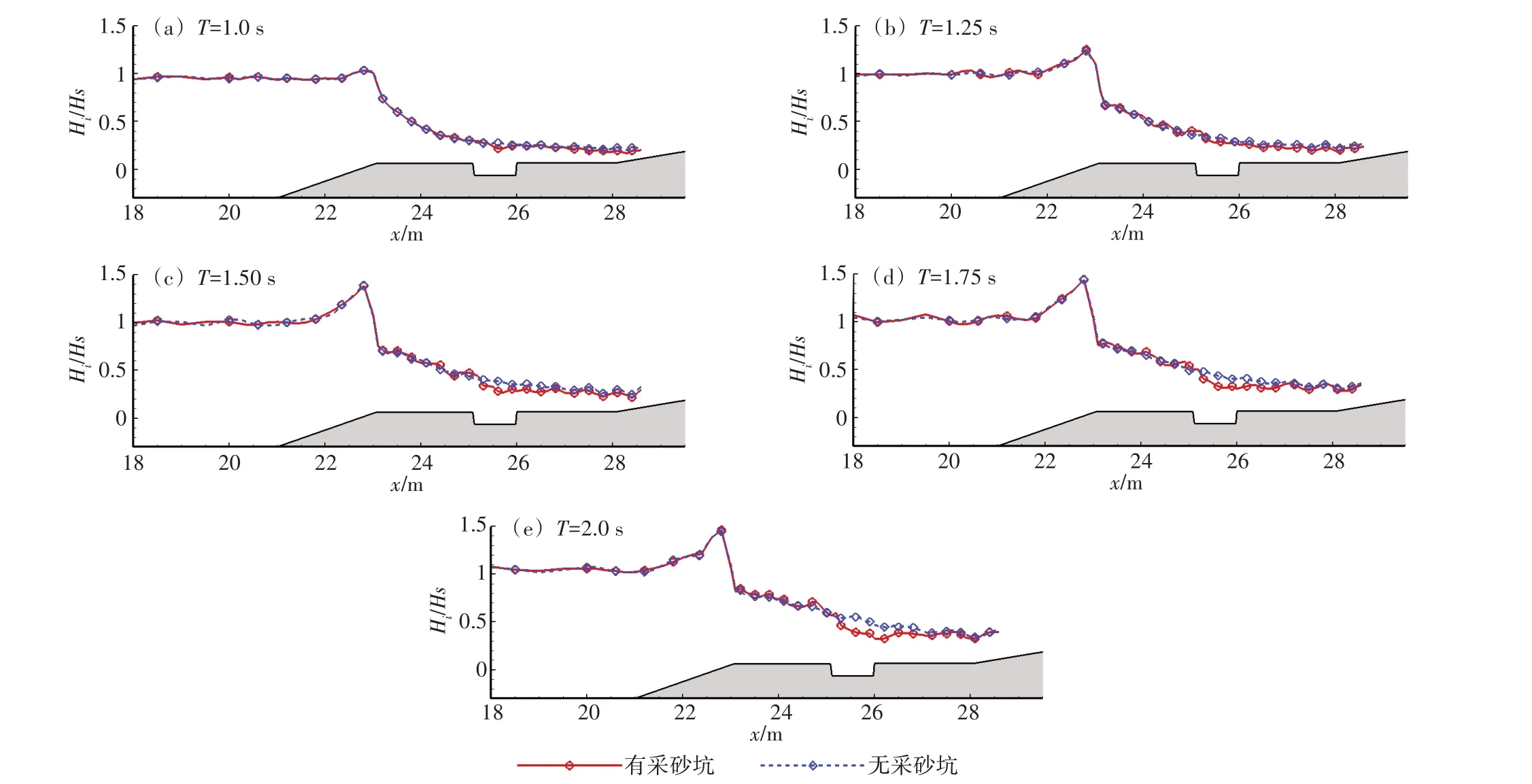
图21 不同波浪周期下局部波高的空间分布

图22 波浪增水随波浪周期的变化

图23 反射系数随波浪周期的变化

图24 规则波的最大平均爬高随波浪周期的变化

4.5 采砂坑位置的影响

本节通过 计 算G1、G2、B3、G3、G4这5 个 工况，研究了不同采砂坑位置对规则波传播演变水动力特性和爬高的影响。图25 展示了不同采砂坑中心位置条件下局部波高的空间分布，结果表明：采砂坑位置对波浪开始的破碎位置不产生影响；随着采砂坑的位置向岸移动，采砂坑对波浪的影响越来越弱，当采砂坑位于礁缘附近时，由于波浪与采砂坑相互作用剧烈，甚至使得采砂坑内的局部波高增大，而当采砂坑靠近岸线附近时影响可以忽略。采砂坑的中心位置由xp= 24.55 m 移至xp= 27.70 m 过程中，采砂坑前局部波高升高范围逐渐变小并且在采砂坑一定区域内局部波高降低的范围也减小。图26 为不同采砂坑中心位置下波浪增水的变化，由图可知，在采砂坑从礁缘移动至岸线附近过程中，波浪增水随xp的增大单调递增，这是因为采砂坑对波浪破碎的影响逐渐变小。图27 展示了反射系数随采砂坑中心位置的变化，当采砂坑在礁缘附近时（xp= 23.50 m）波浪的反射系数最大，随着采砂坑往岸线移动，反射系数的变化呈现出非线性的规律。由图28 可以看出，随着采砂坑的位置向岸移动的过程中最大爬高略有减小，当采砂坑中心位置在25.6 m 以后，采砂坑的位置对波浪最大上升高度的影响可以忽略不计。

图26 波浪增水随采砂坑位置的变化

图27 反射系数随采砂坑位置的变化

图28 规则波的最大平均爬高随采砂坑位置的变化

4.6 采砂坑深度的影响

本 节 通 过 计 算H1、H2、B3、H3、H4、A3这6个工况，研究了不同采砂坑深度对规则波传播演变水动力特性和爬高的影响。图29 为不同采砂坑深度下沿礁局部波高的空间分布，由图可知，当采砂坑深度的增大时，采砂坑前局部波高升高的范围也会增加；采砂坑后一定区域内局部波高降低的范围也增加，且局部波高最大降低幅度也随之增大，当Hp= 0.30 m 时最大降低幅度为30.4%，而Hp= 0.10 m 时降低幅度为17.6%。由图30 可知采砂坑深度的变化对波浪增水几乎没有影响。图31、图32 分别为反射系数随采砂坑深度的变化情况和规则波最大爬高随采砂坑深度的变化规律，随着采砂坑深度的增加反射系数随之增加，最大爬高随采砂坑深度的增加略有减小的趋势，然而，一旦Hp＞0.20 m，采砂坑深度对反射系数和波浪最大上升高度的影响均可以忽略不计，这说明采砂坑深度0.20 m 是一个阈值，随着采砂坑深度从0.10 m 增加到0.20 m，反射系数和波浪最大爬高分别上升了10.1%和下降了10.6%。

图29 不同采砂坑深度条件下局部波高的空间分布

图30 波浪增水随采砂坑深度的变化

图31 反射系数随采砂坑深度的变化

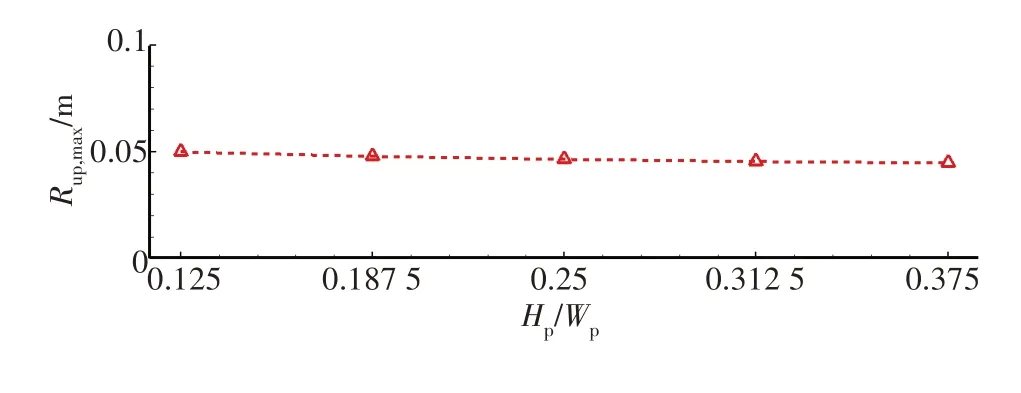
图32 规则波的最大平均爬高随采砂坑深度的变化

4.7 采砂坑宽度的影响

本节通过计算I1、I2、B3、I3、I4、A3这6个工况，研究了不同采砂坑宽度对规则波传播演变水动力特性和爬高的影响。图33 为不同采砂坑宽度下沿礁局部波高的空间分布，如图33 所示，当采砂坑宽度相对较小时，采砂坑内表层高速涌浪与低速水体的质量和动量交换变弱，因此这时采砂坑的存在对局部波高的空间分布的影响略小；随着采砂坑宽度的逐渐增大，采砂坑后一定区域内局部波高降低的范围也会增大，同时局部波高最大降低幅度也呈现相同趋势，当Wp= 1.2 m 时最大降低幅度为29.7%，而Wp= 0.4 m 时降低幅度仅为14.2%。由图34可知随着采砂坑宽度的增大，波浪增水减小，采砂坑宽度从0.4 m 增加到1.20 m时波浪增水降低了3.98%。图35 为反射系数随采砂坑宽度的变化情况，反射系数随着采砂坑宽度的增大先增大后减小，当Wp= 0.6 m 时反射系数最大Kr= 0.112。图36 为波浪最大爬高随采砂坑宽度的变化，结果表明，当Wp＜0.8m时，最大爬高随采砂坑宽度的增加有减小的趋势，然而，一旦坑Wp＞0.8m，采砂坑宽度对波浪最大上升高度的影响可以忽略不计，这说明采砂坑宽度0.8 m是一个阈值。随着采砂坑宽度从0.4 m 增加到0.8 m，波浪最大上升高度下降了6.62%。

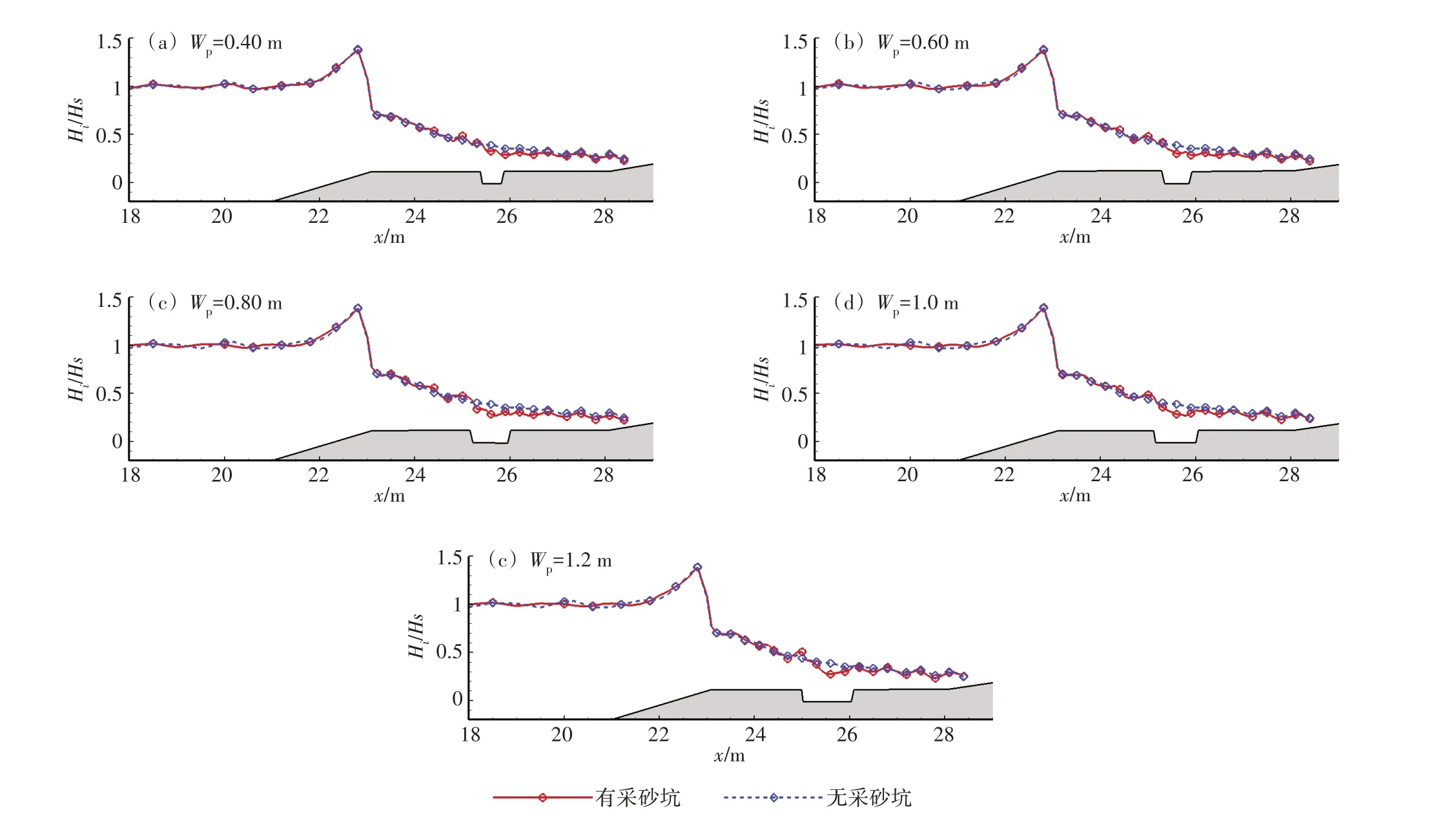
图33 不同采砂坑宽度下局部波高的空间分布

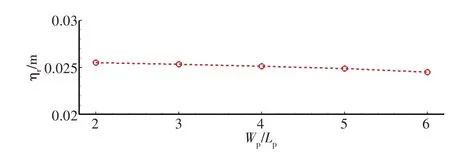
图34 波浪增水随采砂坑宽度的变化

图35 波浪反射系数随采砂坑宽度的变化

图36 规则波的最大平均爬高随采砂坑宽度的变化

5 结论

本文采用非静压模型NHWAVE 系统计算了人工采砂坑对规则波岸礁水动力特性的影响，并与无采砂坑的情况进行了对比分析。主要结论如下：

（1）采砂坑的存在使得坑内的波高局部降低，坑前的波高局部升高，但对岸线附近的波高却无显著影响；坑的存在对波浪增水影响不显著；采砂坑的存在对规则波的反射存在显著影响，在一定程度上增加了波浪的反射；

（2）对具有采砂坑的礁坪而言，入射波高越大：在坑内局部波高降低的范围越大，但降低幅度较小；同时礁坪上的波浪增水也越大，但与无坑时相比几乎相同。礁坪水深发生改变时，沿程波高随着水深的增加而增加，但波浪增水却随着水深增加而减小，相对无坑时的增水值偏低，这种现象在小水深时更明显。随着波浪周期的增大沿程波高也随之增大，同时波浪增水随着周期的增大单调递增，但与无坑时相比区别不明显；

（3）随着采砂坑位置往岸线移动，采砂坑对波浪破碎影响逐渐减小，岸线附近的增水逐渐增大，采砂坑在礁缘附近影响最为明显；采砂坑深度的改变对采砂坑附近的波高影响较大，但对波浪增水无明显影响；当增加采砂坑的宽度时，加大了波浪与采砂坑作用范围，使采砂坑局部波高的变化更大，同时减弱了在岸线附近的平均水位；

（4）对于具有采砂坑的岸礁而言，采砂坑的存在降低了波浪在岸礁上的最大平均爬高，且随着采砂坑从礁缘移动至岸线附近，对最大平均爬高的影响越来越明显，但采砂坑宽度与深度的变化对爬高影响相对较小。