锆合金管塞结构压力电阻焊接头的应力集中系数及影响因素

2024-03-19季顺成张学粮陈兵兵雷永平

机械工程材料 2024年2期

季顺成,张学粮,林健,鲁立,陈兵兵,雷永平,冯刚

(1.北京工业大学材料与制造学部,北京 100124;2. 中广核铀业发展有限公司,北京 100029;3. 苏州热工研究院有限公司,苏州 215004)

0 引言

核电作为一种环保、稳定、高效的洁净新能源,是我国重要的发电形式之一。目前,核电机组正处于快速建设发展中,预计到2035年,在运和在建核电装机容量合计将达到2×108kW[1]。燃料棒包壳是核燃料的第一道安全屏障,其安全性是核电服役安全的关键问题之一。燃料棒包壳常使用锆合金材料并通过压力电阻焊密封连接其管塞结构[2],其接头部位会形成内外部挤出金属,易产生应力集中导致结构断裂失效[3]。填充燃料芯块完成密封焊接后,需要对核燃料棒与燃料棒格架进行组装,从而得到完整的核燃料组件。在组装过程中,需要通过拉棒工艺将燃料棒拉过层层格架;由于格架孔径较小,同时为了减小核燃料棒在服役时的横向移动,在格架上设有刚凸,所以在拉棒、换料等过程中燃料棒会受到较大的拉伸载荷[4-5]。在服役过程中,由于燃料棒内部充有高压氩气,外部有高压水蒸气冲刷,接头在承受内压时也会受到拉伸载荷作用。拉伸载荷易在应力集中处诱发裂纹,导致燃料棒失效,影响核电运行安全,因此研究锆合金管塞结构压力电阻焊接头的应力集中问题是十分必要的。国内外学者常采用有限元方法分析接头应力集中系数,研究应力集中影响因素和改善方法。卫星等[6]使用ANSYS有限元软件建立了钢管混凝土桁架焊接T型管节点模型,研究了轴向拉力作用下管节点热点应力集中系数,结果表明主管应力集中系数受到节点几何参数(尺寸、形状等)的影响较大。HECTORS等[7]研究发现,焊缝几何形状会极大影响应力集中系数的大小和分布以及预期破坏位置。蒋永等[8]和何柏林等[9]得到了焊趾倾角和过渡圆弧半径对钢对接接头应力集中系数的影响规律。陈科等[10]采用椭圆形型线、双曲率型线和流线形型线作为万向十字轴的轴根过渡曲线,有效降低了万向十字轴轴根的应力集中。此外,通过优化焊接处圆弧过渡结构[11]、打磨过渡圆弧[12]、超声冲击处理[13]、降低表面粗糙度[14]等方法可以有效降低焊趾处的应力集中,提高接头疲劳寿命[15]。

作者采用有限元方法建立了管塞结构压力电阻焊接头成形模型和焊后结构应力集中系数计算模型,通过模拟确定了接头应力集中位置并计算其应力集中系数,考虑到内部挤出金属无法通过设计焊接夹具来调整,分析了内部挤出金属过渡角、端塞行进量和包壳管内壁倒角对应力集中系数的影响规律,以期为锆合金管塞结构压力电阻焊的接头设计和制造工艺参数选择提供理论参考。

1 接头应力集中系数的数值模拟

1.1 焊接模型

使用Abaqus有限元分析软件建立锆合金管塞结构压力电阻焊接模型,尺寸参数及接头网格模型如图1所示。轴对称模型(1/2模型)由锆合金端塞、包壳管和纯铜电极夹具组成。端塞为实心圆棒,端设有30°的凸台,电极夹具为空心圆柱体,电极内壁紧贴端塞或包壳管外壁,包壳管伸出电极的长度为1 mm。接头附近网格进行加密处理,最小网格尺寸为0.035 mm,模型共计19 972个单元,20 467个节点。

采用顺序耦合的方式对模型进行电-热-力三场耦合,模拟锆合金管塞结构接头成形过程。首先进行电-热耦合,采用DCAX4E单元类型,在端塞侧电极夹具两端施加800 A的集中电流,将包壳管侧电极夹具边缘设为零电势面,端塞与包壳管接触位置设置接触电阻,电流可以通过接触面产生电阻热,以达到焊接温度;随后进行热-力耦合,采用CAX4R单元类型,将包壳管侧末端固定,在端塞末端施加1 500 N的均布载荷,将电-热模拟结果中的网格温度赋予网格,最终实现电-热-力三场耦合,完成对焊接过程的全流程模拟。参考文献[16],模拟时相关材料的物理、力学性能见图2。

图2 试验合金的物理及力学性能Fig.2 Physical and mechanical properties of test alloy: (a) heat conductivity, density, specific heat capacity, conductivity and (b) thermal expansion coefficient, elastic modulus, yield strength

1.2 焊接模型验证

采用Gleeble 1500D型热模拟试验机对锆合金管塞结构压力电阻焊过程进行热模拟试验,载荷为1 500 N,测温点位于距端塞凸台1 mm处,测温点温度为750 ℃,升温时间为0.3 s,焊接时间为0.5 s;通过输入大电流在端塞和包壳管的接触面上快速产生较大的电阻热,使接头处迅速达到塑性状态,在力和热的共同作用下发生变形,形成原子间结合,完成焊接。试验结束后采用线切割法将接头沿轴线切开,制取金相试样,经打磨、抛光、HNO3+H2O+HF(体积比为9…9…2)溶液腐蚀后,采用Gemini SEM 300型扫描电子显微镜观察形貌。采用电-热-力耦合模型[16]模拟接头形貌,如图3所示,可见:试验所得接头宏观形貌与模拟宏观形貌吻合,在包壳管内外侧均出现挤出金属;试验和模拟所得内部挤出金属高度分别为146,132 μm,两者相对误差为9.58%,外部挤出金属高度分别为449,481 μm,两者相对误差为6.65%。由上可知,宏观形貌试验结果与模拟结果相差较小,说明可以通过电-热-力耦合模型模拟压力电阻焊接过程,得到接头形貌。

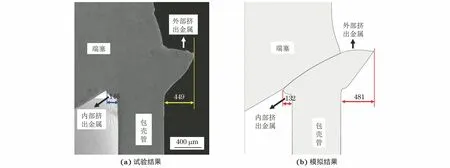
图3 试验与模拟所得接头宏观形貌Fig.3 Test (a) and simulation (b) results of macro morphology of joint

1.3 应力集中系数计算方法

应力集中是一种结构局部最大应力大于平均应力的现象,在承载状态下应力集中点处易产生裂纹,进而导致断裂。应力集中系数Kt的计算公式[13]如下:

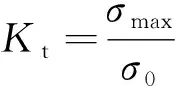
(1)

式中:σmax为最大应力值;σ0为平均应力值。

有限元模拟得到接头在拉伸载荷作用下轴向应力分布云图,并根据式(1)计算得到应力集中系数。

将接头网格模型中的端塞和包壳管单元导入应力集中系数计算模型(见图4),将端塞末端固定,在包壳管末端施加200 MPa的轴向拉伸应力,接头焊接面采用绑定约束,采用CAX4R单元类型。同时,仅保留内部挤出金属部分,简化应力集中计算模型中与研究关联较小的基体部分,建立应力集中系数计算简化模型,研究应力集中系数的影响因素,材料参数及边界条件等保持不变。

图4 在轴向拉伸载荷作用下的接头应力集中系数计算模型及简化模型Fig.4 Calculation model (a) and simplified model (b) of stress concentration factor of joint under axial tensile load

2 应力集中系数的影响因素

2.1 内部挤出金属过渡角

内部挤出金属过渡角是接头应力集中系数的重要影响因素,过渡角定义如图5(a)所示。采用应力集中系数计算简化模型计算不同过渡角下的接头应力集中系数。由图5(b)可见:当过渡角为10°时,接头的应力集中系数最大,为2.082;过渡角为10°～60°时,应力集中系数整体呈下降趋势,除了在30°处略有升高;过渡角为60°～120°时,应力集中系数上升;当过渡角大于120°时,应力集中系数下降,在170°处最低,相较于最大值下降了31.0%。由此可知,过渡角对锆合金管塞结构压力电阻焊接头应力集中系数影响较大,并呈现一定的规律性。

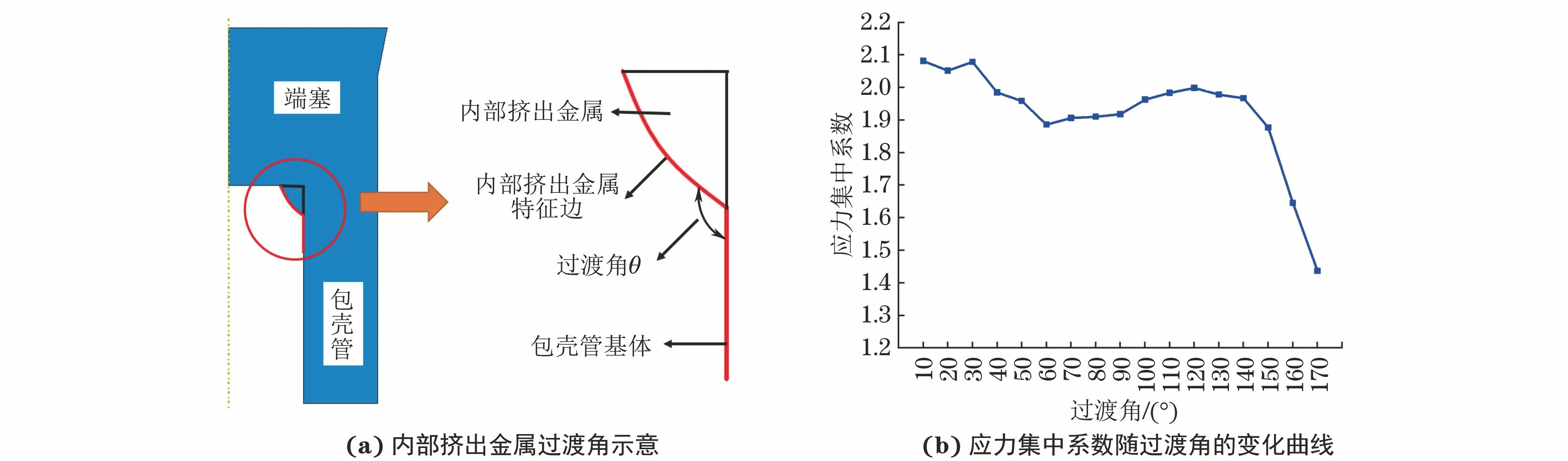
图5 内部挤出金属过渡角示意及接头应力集中系数随过渡角的变化曲线Fig.5 Diagram of transition angle of internal extruded metal (a) and stress concentration factor vs transition angle curve of joint (b)

2.2 端塞行进量

端塞行进量是指焊接完成时端塞末端端面在压力作用下的轴向位移量,在其他参数不变的情况下,端塞行进量会对接头形状产生较大的影响。将端塞末端的载荷控制改为位移控制,总位移设为0.3 mm,与载荷控制下端塞的最终位移相同,采用应力集中系数计算模型计算可得端塞行进量分别为0.025,0.080,0.135,0.190,0.245,0.300 mm的接头在拉伸载荷下的轴向应力分布。由图6可知:当端塞行进量为0.025 mm时,内部挤出金属过渡角处的局部应力较小(最大为327.3 MPa),应力最大值出现端塞焊接面处,为359.9 MPa;随着端塞行进量增加,内部挤出金属过渡角处的最大应力逐渐增大,当端塞行进量为0.3 mm时达到392.5 MPa。

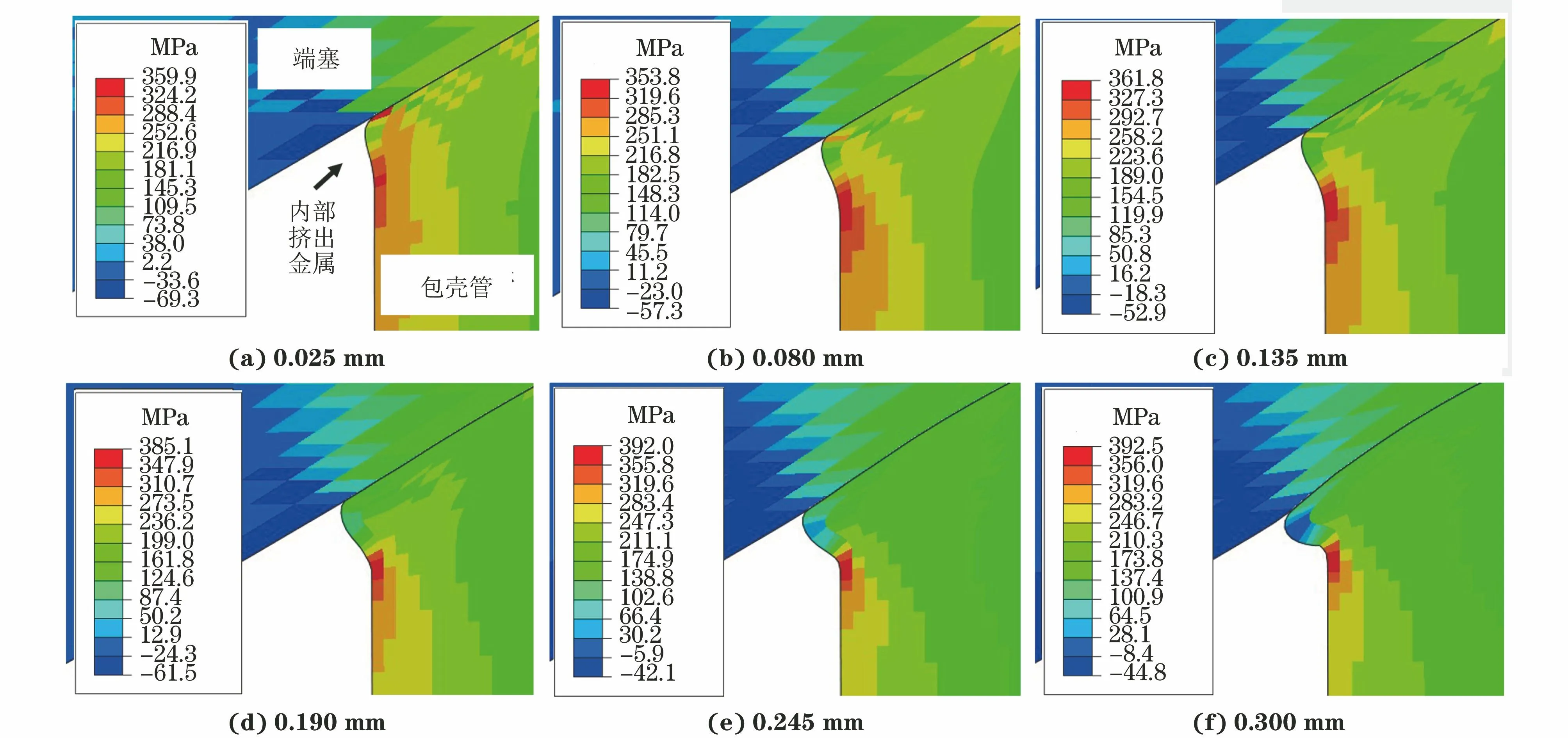
图6 不同端塞行进量焊接接头在拉伸载荷下的轴向应力分布Fig.6 Axial stress distribution of welded joints with different end plug displacement under tensile load

由图7可知:随着端塞行进量增加,内部挤出金属过渡角从172.19°逐渐降至143.14°,应力集中系数增大,接头熔合线长度增大;当端塞行进量为0.025 mm时,熔合线长度为0.66 mm,未超过包壳管壁厚0.7 mm。这表明通过减小端塞行进量可以增大过渡角,从而降低接头的应力集中系数;但当端塞行进量过小时,形成的熔合线长度较短,导致接头承载能力下降。因此在选择工艺参数时,需要综合考虑端塞行进量对熔合线长度和应力集中系数的影响,即在保证应力集中系数满足使用需求的条件下,尽量增大熔合线长度。

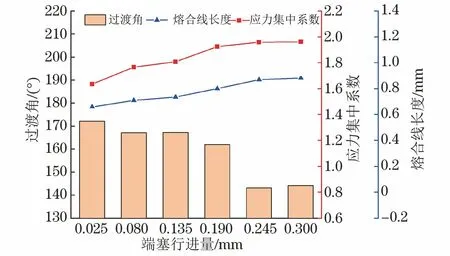
图7 不同端塞行进量下接头的应力集中系数、内部挤出金属过渡角与熔合线长度Fig.7 Stress concentration factor, transition angle of internal extruded metal and fusion line length of joint under different end plug displacement

2.3 包壳管内壁倒角尺寸

包壳管内壁倒角为平面型倒角,如图8所示,x,y分别为倒角宽度和倒角深度。设计了8种尺寸包壳管内壁倒角,以研究其对应力集中系数的影响。由图9可见:倒角宽度对接头形貌的影响较小,而随着倒角深度增加,内部挤出金属体积逐渐减小,当倒角深度为0.50 mm时,内部挤出金属过渡较平滑,当倒角深度大于0.50 mm时,接头产生间隙,强度受到影响;当倒角深度不大于0.50 mm时,应力集中发生在内部挤出金属过渡角处,而当倒角深度大于0.50 mm时,应力集中位置转移至包壳管倒角面与端塞端面的过渡处。

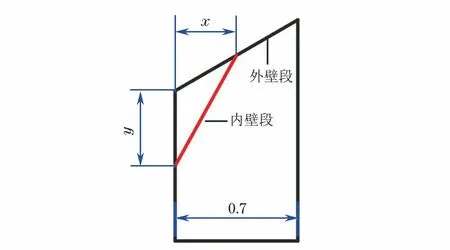
图8 包壳管内壁倒角尺寸Fig.8 Size of cladding tube inner wall chamfer

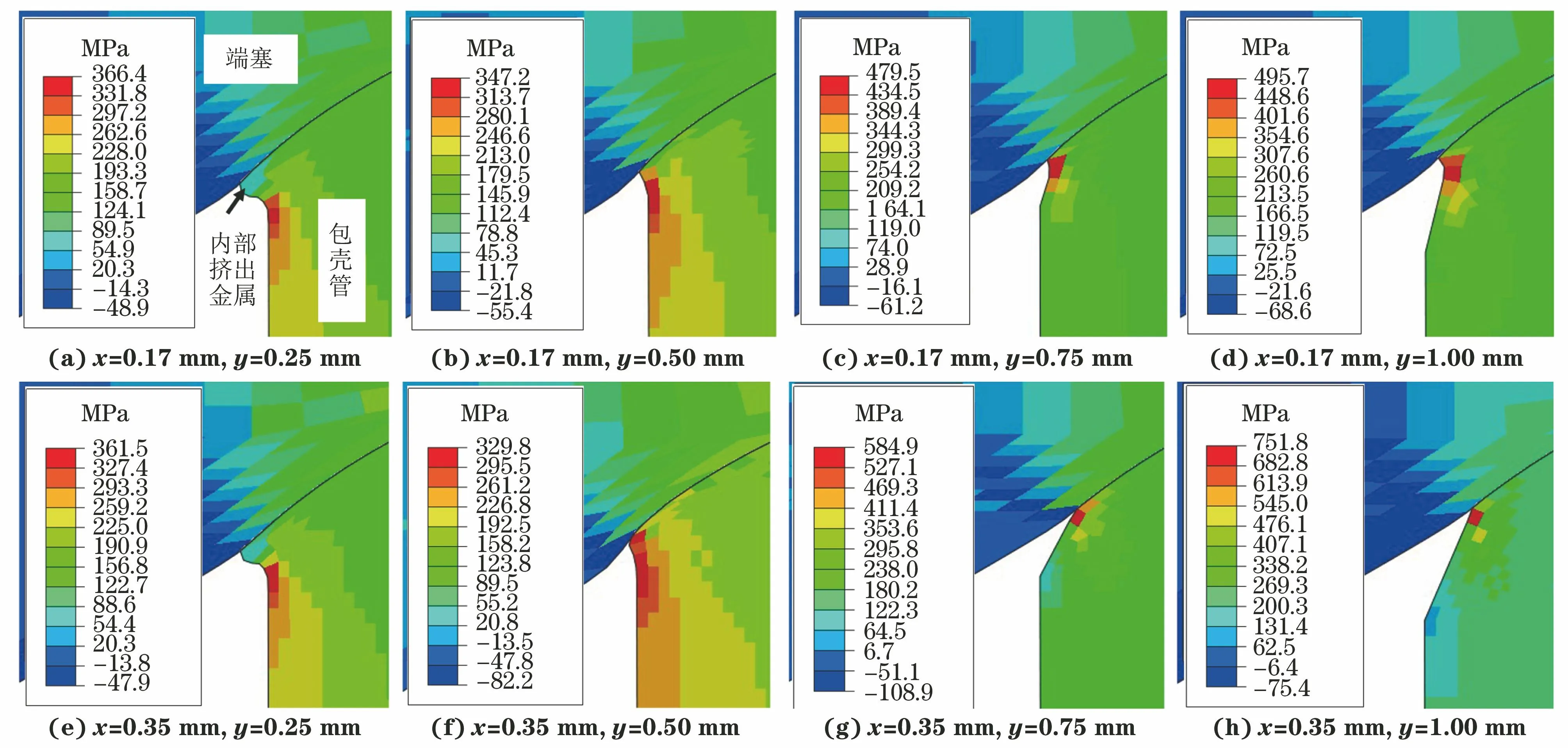
图9 不同倒角尺寸接头在拉伸载荷作用下的轴向应力云图Fig.9 Axial stress cloud diagram of joints with different chamfer size under tensile load

未倒角接头的应力集中系数为0.884,熔合线长度为1.963 mm。由图10可知:当倒角深度不大于0.50 mm时,接头的应力集中系数相比未倒角接头降低,其中倒角宽度为0.17,0.35 mm,倒角深度为0.50 mm时接头的应力集中系数降低效果最为显著,分别降低了16.00%,11.56%,形成的内部挤出金属过渡角较大,分别为167.29°,163.59°,而未倒角接头的过渡角仅为144.63°。由前文可知,当内部挤出金属过渡角大于120°时,接头的应力集中系数随着过渡角的增大而降低。因此,可以通过设计包壳管的倒角形状来降低接头应力集中系数。当倒角深度大于0.50 mm时,接头的应力集中系数显著高于未倒角接头,最大提高了91.49%,主要原因在于当倒角过深时,包壳管变形量不足以形成内部挤出金属,应力集中位置从过渡角处转移至包壳管倒角面与端塞端面的过渡处,且由于在接头处形成间隙,导致接头处的过渡角较小,进而造成接头的应力集中程度比未倒角时更高。