中锰钢棘轮行为的细观有限元模拟

2024-03-19畅舒心刘骏华黄兴民

机械工程材料 2024年2期

畅舒心,张娟,刘骏华,黄兴民

(西南交通大学1.力学与航空航天学院,应用力学与结构安全四川省重点实验室;2.材料科学与工程学院,成都 610031)

0 引言

中锰(锰质量分数在4%～12%)钢因存在相变诱发塑性(TRIP)效应而具有高强高韧性,在汽车工业、国防工业等领域得到越来越多的应用[1-2]。钢结构件在加工成形以及实际服役时不可避免会产生较大的变形以及承受循环载荷;在非对称应力控制循环加载下,结构件会产生塑性变形的累积现象,即棘轮效应[3]。棘轮效应中产生的渐进变形,即棘轮应变的累积会加速疲劳裂纹扩展和损伤累积,导致结构件疲劳寿命缩短或使其塑性变形远超限值,这是工程应用中不可忽略的重要问题之一[4-5]。由于中锰钢由残余奥氏体、铁素体等多种相组成,并且在变形过程中会发生马氏体相变,因此其力学行为比一般钢材更为复杂。另外,在循环载荷作用下,这种复杂的显微组织演变也势必会对其棘轮行为产生影响。然而,目前能够探究变形过程中材料内部微结构受力的原位试验设备还较少[6],且成本较高,这使得通过试验方法来研究中锰钢棘轮变形过程中的显微组织演变较为困难。随着计算机性能的进一步提高,有限元模拟凭借直观易得、节约成本的优势逐渐成为探究中锰钢变形行为的有力工具[7]。

国内外学者针对TRIP钢单轴拉伸过程中组织演变对力学性能影响的有限元模拟研究较多。DAN等[8]采用有限元模拟对TRIP钢板成形过程中应变诱发马氏体相变效应进行了研究。LIU等[9]提出了一种描述马氏体相变导致残余奥氏体晶粒尺寸演变的新方法,并以此为基础,采用有限元方法对多相钢的力学行为进行了数值模拟。PAPATRIANTAFILLOU等[10]采用非线性复合材料的均匀化技术建立了多相TRIP钢的本构方程,模拟了TRIP钢单轴拉伸过程中的变形特征,发现TRIP效应能够延缓颈缩的发生。SEERI等[11-12]采用ABAQUS有限元软件分析了马氏体相变对TRIP钢成形性能的影响,并进一步模拟了杯突拉伸试验,研究了相变应变的影响以及相变动力学的应力状态依赖性。以上基于宏观模型的模拟通常只能预测材料组织演变的综合统计信息,无法描述微观结构信息,如显微组织形貌特征、织构以及相变区域分布等。为了更好地揭示显微组织演变对中锰钢宏观力学性能的影响,学者们开始建立基于材料真实微观结构的细观有限元模型。孙宇阳等[7]基于试验得到的中锰钢显微组织建立了代表性体积元(RVE)模型,采用ABAQUS软件对中锰钢在单轴拉伸过程中的组织演变和应力、应变分布进行了模拟。董瑞[13]利用电子背散射衍射(EBSD)采集的中锰钢显微组织图像建立了RVE模型,分析了单双轴拉伸变形过程中马氏体相变的形核位置、扩展方向及变形过程中应力和应变的分布。HOSSEINABADI等[14]基于TRIP800钢的微观结构,引入应变诱发马氏体相变动力学模型,建立了单轴拉伸下TRIP效应产生过程的细观有限元模型,并预测了马氏体的初始形核区域。LATYPOV等[15]基于中锰钢真实显微组织建立了细观有限元模型,将基于等功原理的均匀化本构模型引入奥氏体单元中,模拟发现了TRIP效应产生过程中铁素体与奥氏体组织之间应变局部化的交替特征,即在低应变时,应变基本集中在奥氏体中,随着奥氏体发生应变硬化并在加载过程中转变为马氏体,外部施加的变形越来越多地被铁素体所容纳。

以上研究大都是单轴拉伸载荷下的有限元模拟,而有关循环载荷作用下中锰钢棘轮行为有限元模拟的研究较少。为此,作者以含铝中锰钢为研究对象,基于扫描电镜得到的显微组织构建二维RVE模型,同时引入马氏体相变演化方程,采用Mori-Tanaka均匀化方法构建了奥氏体和马氏体组合相的本构模型,采用细观有限元方法研究了非对称应力控制加载下中锰钢显微组织的应力、应变场分布以及相变对棘轮行为的影响。

1 试样制备与试验方法

试验材料为含铝中锰钢,化学成分(质量分数/%)为6.9Mn,3.2Al,0.35C,余Fe。采用80 kg真空感应炉熔炼并浇铸在金属型中得到直径为140 mm的钢锭。利用机加工去除钢坯表面氧化皮,在加热炉中于1 200 ℃下保温2 h,锻成截面尺寸为50 mm×30 mm的中间坯。在二辊可逆式试验轧机上进行轧制,初轧温度为1 050 ℃,轧至厚度为80 mm,降温至900 ℃,再轧至厚度为12 mm,终轧温度为750 ℃,水冷至室温。在箱式加热炉内进行700 ℃×1 h的临界退火,水淬至室温。

制取金相试样,经逐级打磨、机械抛光、体积分数4%的硝酸乙醇溶液腐蚀后,采用ZEISS SUPRA 55型场发射扫描电镜(SEM)观察微观形貌。采用Bruker D8 Advance型X射线衍射仪(XRD)进行物相分析,钴靶,Kα射线,扫描范围为40°～120°,扫描速率为2(°)·min-1,根据YB/T 5338-2006计算残余奥氏体体积分数,选取同条件的3个试样的XRD谱进行计算,以保证准确性。沿轧制方向制取哑铃棒状试样,如图1所示,标距段为光滑棒状,尺寸为φ6 mm×20 mm,夹持端为螺纹状,采用MTS809A/T型拉扭试验机进行单轴拉伸试验和非对称应力循环试验(棘轮试验),试验温度为室温,力加载方向与试样轴向平行。单轴拉伸试验的应变速率为5×10-3s-1,棘轮试验平均应力为50 MPa,应力幅分别为700,710 MPa,分别记为(50±700),(50±710) MPa工况,加载速率为80 MPa·s-1。

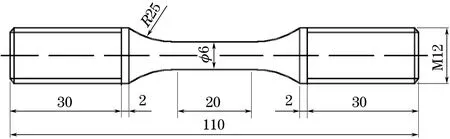
图1 单轴拉伸试样和棘轮试样的尺寸Fig.1 Size of uniaxial tensile sample and ratcheting sample

2 有限元模拟

2.1 建立RVE模型

由图2计算可得试验钢中的残余奥氏体体积分数最大值为47.34%,最小值为39.30%,平均值为42.94%。根据SEM形貌建立RVE模型,由于只有RVE模型尺寸达到某一临界值时,才能较好反映显微组织基本信息[16],因此需要在SEM图像中合理选择建模区域。选择RVE模型尺寸为12 μm×12 μm,所选区域奥氏体体积分数为45%,与试验测得平均值接近,相对误差小于5%。将图3(a)进行图像处理以使两相组织明显区分,利用程序拾取两相组织边界并转化为矢量文件,后导入ABAQUS软件中建立草图和二维方形部件,使用草图切割部件,建立基于真实显微组织的RVE模型,如图3(b)所示,其中暗黑色凹面和亮灰色凸面区域分别为铁素体和奥氏体。RVE模型采用对称性边界条件,在右侧边界施加均布载荷,采用三角形为主的网格划分方法,如图3(c)所示,单元类型为CPE3,共包含24 409个单元。

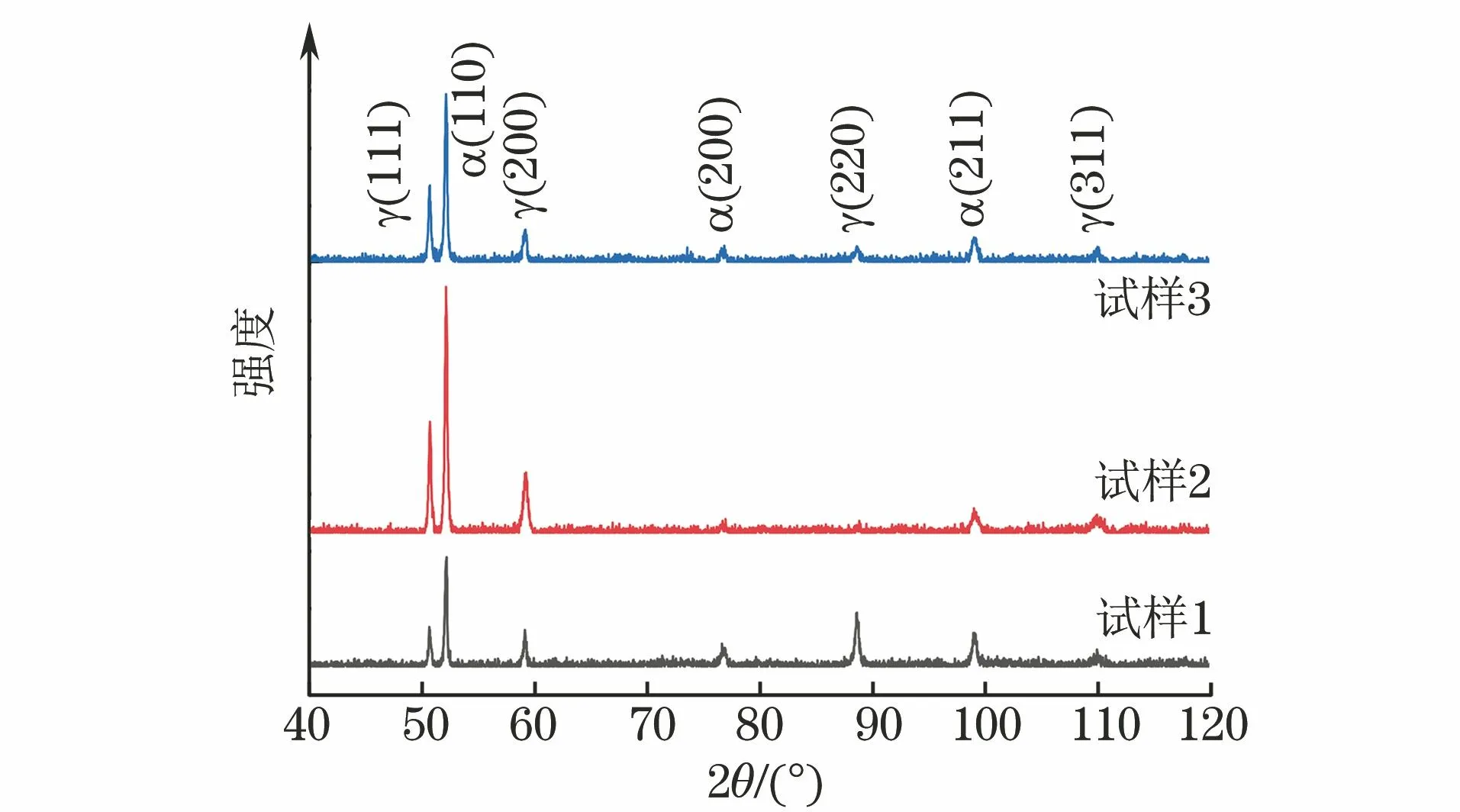
图2 试验钢不同试样的XRD谱Fig.2 XRD patterns of different test steel samples

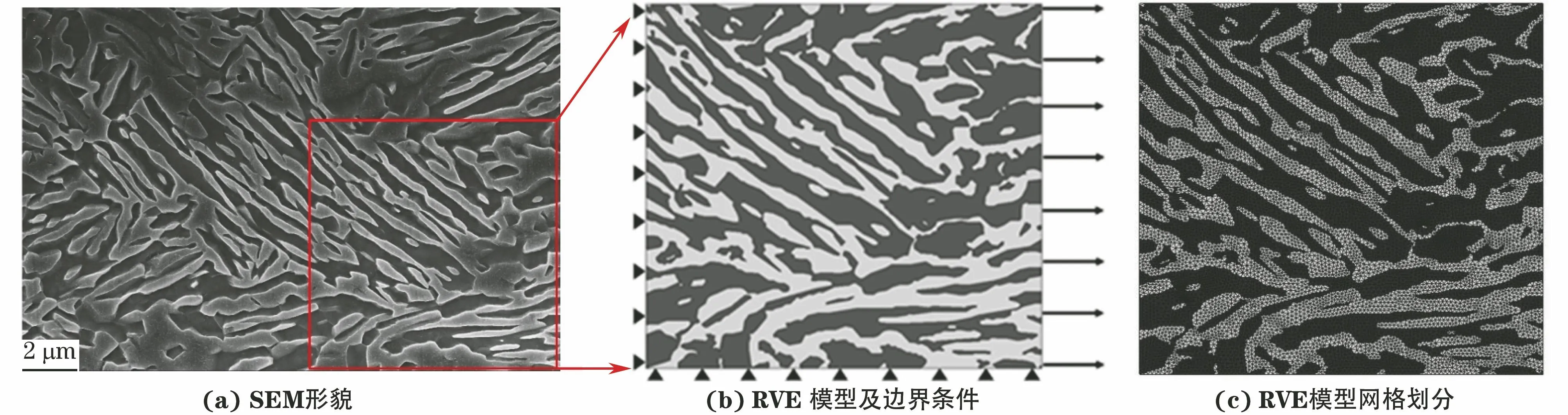
图3 试验钢的SEM形貌、 RVE模型及边界条件、RVE模型网格划分Fig.3 SEM morphology (a), RVE model and boundary conditions (b) and RVE model meshing (c) of test steel

2.2 奥氏体和马氏体组合相的均匀化本构模型

承受载荷时,残余奥氏体发生的马氏体相变对中锰钢的变形行为有十分重要的影响。然而,采用细观有限元方法直接模拟马氏体相变非常困难,需要采用间接方法,即Mori-Tanaka均匀化方法来求解含夹杂材料基体的平均内应力,通过与局部扰动应力相加获得基体中实际应力。均匀化方法简单,能反映复合材料中夹杂相之间的相互作用[17-18]。

将残余奥氏体视为弹塑性基体相,将相变产生的马氏体视为纯弹性球形夹杂相,应用Mori-Tanaka均匀化方法得到奥氏体和马氏体组合相(奥马组合相)的均匀化本构模型,并在模型中引入相变演化方程,以此来模拟马氏体相变对材料力学性能的影响[18]。对组合相本构模型编写ABAQUS子程序UMAT来进行有限元移植,赋予RVE模型中的奥氏体单元。奥氏体和马氏体的弹性模量均取219 GPa,铁素体取203 GPa,各相泊松比均取0.33。

采用循环弹塑性本构模型来描述铁素体和奥氏体的循环变形行为,模型主控方程[17]如下:

ε=εp+εe

(1)

σ=Ce1:εe

(2)

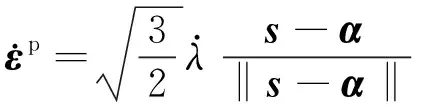
(3)

(4)

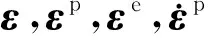
采用修正的Abdel-Karim-Ohno非线性随动硬化模型描述材料的棘轮行为。将背应力张量α分成M份,即

(5)

(6)

μ=μ0exp(-kp)

(7)

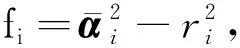
其中,M取6;铁素体的r1,r2,r3,r4,r5,r6分别为323.6,128.3,27.8,16.7,5.6,3.3,ξ1,ξ2,ξ3,ξ4,ξ5,ξ6分别为3.8,62,36,29.7,56.1,16.6;奥氏体r1,r2,r3,r4,r5,r6分别为330.6,136.3,27.8,16.7,5.6,3.3,ξ1,ξ2,ξ3,ξ4,ξ5,ξ6分别为2.2,66,36.2,29.8,75.1,19.8。

采用Mori-Tanaka均匀化方法进行奥马组合相的均匀化处理,已知宏观应变速率时,奥马组合相的宏观应力速率计算公式[17]如下:

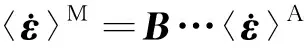
(8)

(9)

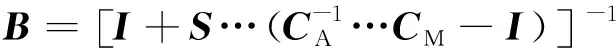
(10)

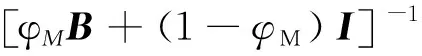
(11)

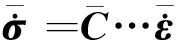
(12)

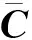
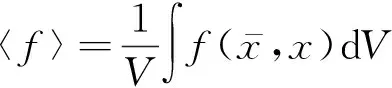
(13)

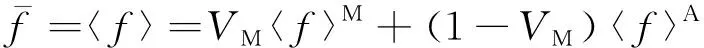
(14)

式中:V为RVE模型的体积;VM为相的体积。

2.3 马氏体相变演化方程

变形过程中中锰钢中的残余奥氏体会发生马氏体相变,马氏体含量是变化的。因此,在上述均匀化模型中必须考虑每一个计算的增量步中马氏体含量的变化,这就需要构建合理的马氏体相变演化方程来对奥氏体和马氏体体积分数进行动态更新。

单轴拉伸变形时中锰钢的相变演化规律可以用指数函数[19]来描述,如下:

φMT=1-exp(zεp)

(15)

式中:φMT为奥氏体向马氏体的转变体积分数;z为拟合系数,取—2.76;εp为塑性应变。

由于循环加载的往复性,使用简单的指数函数建立相变演化方程将不再合理,还需要考虑加载方式、循环圈数、加载幅值和累积塑性应变等对马氏体相变的影响[19-20]。根据试验测得中锰钢循环过程中马氏体的体积分数变化,选择文献[21-22]中的循环加载马氏体相变演化方程,如下:

VMT=-c[1-exp(-ΦSp)]m

(16)

式中:Sp为累积塑性应变;c,Φ,m为待定系数。

(50±700) MPa和(50±710) MPa工况下,系数c分别为0.65和1.18,Φ分别为0.129和-0.082,m均取1.6。

3 结果与讨论

3.1 单轴拉伸行为

采用图3中的RVE模型对试验钢进行单轴拉伸有限元模拟,所得真应力-真应变曲线及相应的试验曲线如图4所示。相比不考虑马氏体相变,考虑马氏体相变模拟的真应力-真应变曲线与试验曲线吻合较好,相对误差小于5%,单轴拉伸后期曲线均呈现明显的应变硬化现象,说明模型可以对TRIP效应进行准确描述。此外,提取拉伸至25%应变时每个奥氏体单元的马氏体体积分数并取平均值,得到奥氏体中马氏体的体积分数为52.7%。XRD测得未变形和25%应变时试验钢的残余奥氏体体积分数分别为42.94%,21.84%,则发生马氏体相变的体积分数占初始残余奥氏体体积分数的49.1%,和模拟结果的相对误差小于10%,说明RVE模型对马氏体体积分数的预测较为准确。

图4 模拟与试验得到的试验钢单轴拉伸真应力-真应变曲线Fig.4 True stress-true strain curves of test steel in uniaxial tension obtained by simulation and test

由图5可见:当应变为5%时,高应力区域主要集中在铁素体内;随着应变增大,部分奥氏体发生马氏体相变,奥氏体内的应力逐渐增大,当应变为25%时,奥氏体内的应力超过了铁素体内的应力。

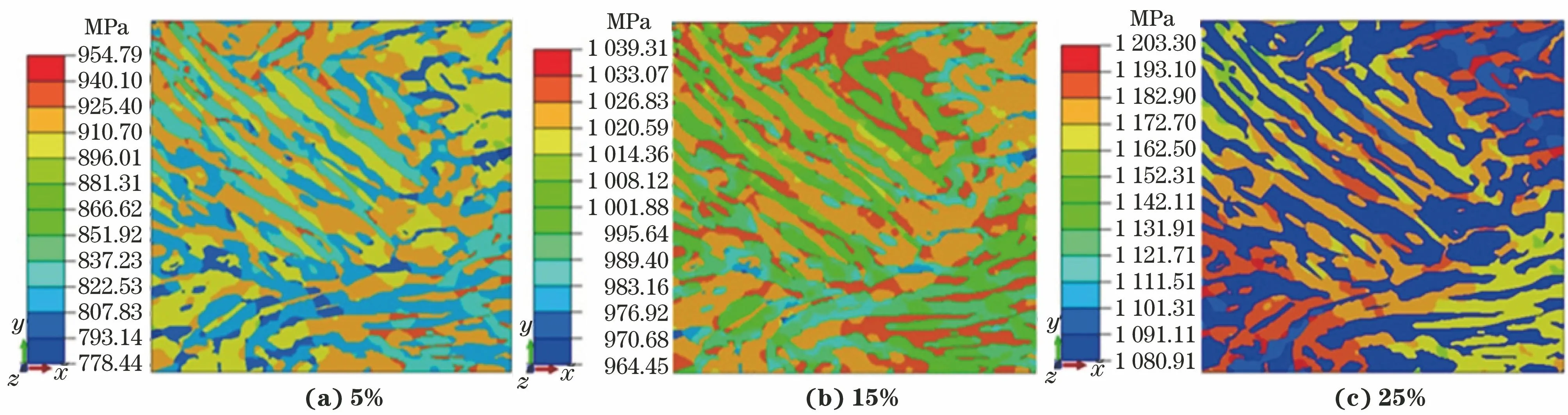
图5 模拟得到拉伸至不同应变时试验钢的Mises等效应力分布Fig.5 Mises equivalent force distribution of test steel after tension to different strains obtained by simulation

采用均匀化方法提取奥氏体与铁素体两相在不同应变下的平均应力。由图6可知:变形初期,奥氏体由于屈服强度较低,在相同的应力下先产生了塑性变形,铁素体由于屈服强度较高而承受较高的应力水平;随着应变增加,奥氏体发生马氏体相变,塑性变形快速增大,并产生了较明显的应变硬化现象;当应变为17%左右时,两相的平均应力相等;随着应变继续增加,马氏体进一步生成,奥氏体平均应力超过铁素体,高应力区从铁素体转移至奥氏体。可见拉伸过程中,奥氏体与铁素体两相之间出现了应力交替现象。

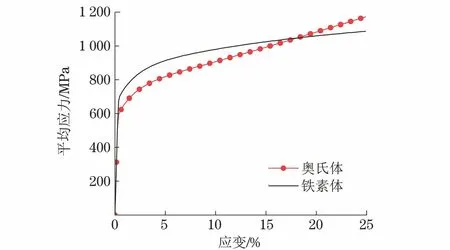
图6 模拟得到奥氏体和铁素体的平均应力-应变曲线Fig.6 Average stress-strain curves of austenite and ferrite obtained by simulation

3.2 棘轮行为

由图7可见:无论是否考虑马氏体相变,模拟得到两种工况下的应力-应变曲线变化趋势几乎一致,滞回环随循环圈数的增加逐渐增大;相同工况下,在循环初始阶段,考虑马氏体相变模拟的滞回环与不考虑相变时几乎重合,随着循环圈数增加,两者之间逐渐产生差异,考虑相变模拟的滞回环面积小于不考虑相变模拟的,而且当应力幅更大时,这种差异也更加明显。

图7 不同工况下考虑与不考虑马氏体相变模拟得到的应力-应变滞回环Fig.7 Stress-strain hysteresis loops with and without consideration of matensitic transformation under different working conditions obtained by simulation

由图8可见:两种工况下,考虑相变模拟和试验得到的棘轮应变均随循环圈数的增加而增大,变化趋势一致,说明此模拟能在宏观层面上较合理地描述材料的棘轮行为。当工况为(50±700) MPa时,根据式(16)计算可得循环第50圈时马氏体体积分数为8.1%,与试验结果(8.3%)的相对误差为2.4%;当工况为(50±710) MPa时,马氏体体积分数计算结果为16.3%,试验结果为18.3%,相对误差为10.2%,较为接近。这说明所采用的细观本构模型可以定性地描述不同工况下马氏体相变对中锰钢棘轮行为的影响。当工况为(50±700) MPa时,考虑、不考虑相变模拟的棘轮应变演化曲线几乎重合,只是随循环圈数的增加,考虑相变模拟得到的棘轮应变略低于不考虑相变模拟结果;当工况为(50±710) MPa时,不考虑相变模拟得到的棘轮应变随循环圈数增加而增大的趋势(应变增长率)明显高于考虑相变时。

图8 不同工况下考虑与不考虑马氏体相变模拟和试验所得棘轮应变随循环圈数的演化曲线Fig.8 Evolution curves with and without consideration of matensitic transformation of ratcheting strain vs cycle numbers obtained by simulation and test under different working conditions

由图9可知:奥氏体、铁素体中的Mises等效应力分别为700,800 MPa左右;在第1圈循环结束后,奥氏体和铁素体中的Mises等效应力呈现不均匀分布特征;当循环圈数达到第25圈时,这种不均匀特征尤为明显;随着循环继续进行,铁素体中的不均匀性逐渐减小(图中椭圆标记区),奥氏体中则逐渐增大(图中矩形标记区),说明这种应力分布的不均匀特征和马氏体相变有关。由图10可见:不论是否考虑相变,奥氏体的平均应力模拟结果整体上小于铁素体;考虑相变模拟的奥氏体平均应力随循环圈数的增加而增加,而铁素体平均应力随循环圈数的增加而减小,这可能是因为在应力控制的加载条件下,相变产生的马氏体使奥氏体承担应力增大,而由于外部施加峰值应力保持不变,导致铁素体承担应力减小。经计算可得奥氏体平均应力增大值与铁素体平均应力减小值相同。

图9 模拟得(50±710) MPa工况下循环不同圈数时试验钢的Mises等效应力、累计塑性应变、马氏体体积分数的分布Fig.9 Simulated Cloud distribution of Mises equivalent force (a-c), cumulative plastic strain (d-f) and martensite volume fraction (g-i) of test steet after cycle different circle nuambers under (50±710) MPa: (a,d,g) 1 cycle; (b,e,h) 25 cycles and (c,f,i) 50 cycles

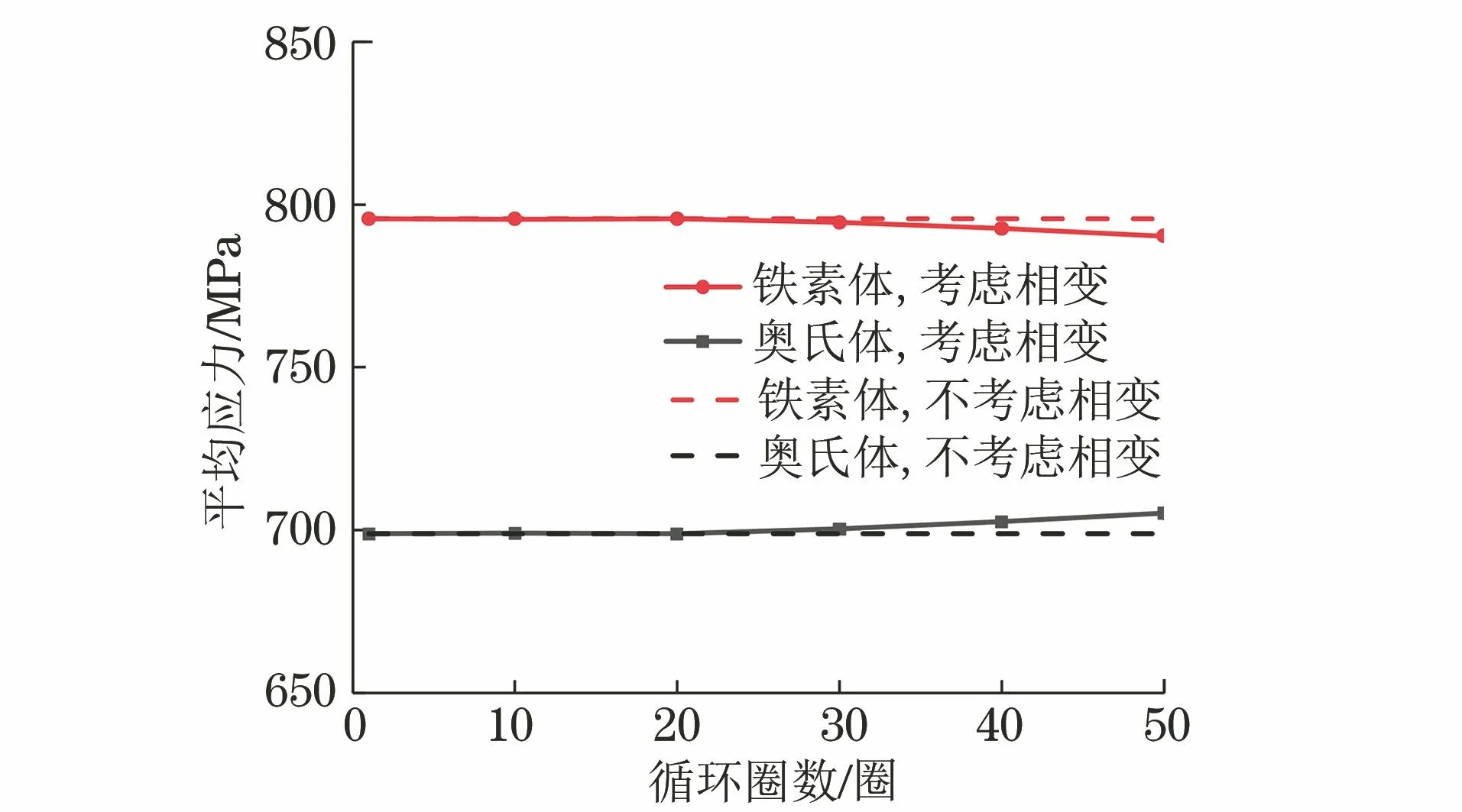
图10 (50±710) MPa工况下奥氏体和铁素体在峰值应力下模拟得到平均应力随循环圈数的演化曲线Fig.10 Evolution curves of average stress vs cycle numbers of austenite and ferrite obtained by simulation when reach peak stress under different working conditions

循环1圈时,试验钢中并未出现较明显的累积塑性应变,也未发生马氏体相变;而随着循环的进行,马氏体体积分数明显增加,累积塑性应变逐渐增加,且由于发生了马氏体相变,奥氏体中的累积塑性应变也呈现出不均匀分布特征;当循环圈数增加到50圈时,奥氏体中累积塑性应变的不均匀分布特性也更明显,导致其邻近的铁素体内的塑性变形也出现不均匀分布;奥氏体中累积塑性应变较大的区域多分布在马氏体含量较多的位置(图中矩形标记区)。这进一步说明基于真实显微组织的细观有限元模拟方法可以反映棘轮行为中由于马氏体相变产生的微观特性。