基于格子Boltzmann 方法的钉扎螺旋波反馈控制*
2024-03-19赖瑶瑶陈鑫梦柴振华施保昌
赖瑶瑶 陈鑫梦 柴振华 施保昌†
1) (华中科技大学数学与统计学院,武汉 430074)
2) (华中科技大学,工程建模与科学计算湖北重点实验室,武汉 430074)
3) (华中科技大学,数学与应用学科交叉创新研究院,武汉 430074)
螺旋波是心室跳动过速和纤维性颤动的根源,钉扎螺旋波相对于自由螺旋波来说更难消除.本文采用格子Boltzmann 方法求解,以FitzHugh-Nagumo 模型为对象,研究了使用反馈控制法消除钉扎螺旋波.数值结果表明,无论钉扎螺旋波钉在圆形障碍物还是矩形障碍物上,反馈控制法对其都具有很好的控制作用.此外,通过数值模拟系统研究了可激性系数、反馈控制信号幅度、记录反馈信号时间和障碍物的大小对钉扎螺旋波的控制情况.研究表明,钉扎螺旋波消除有三种情况.首先,反馈控制信号幅度和可激性系数与钉扎螺旋波消除所需的时间有关,反馈控制信号幅度越大或可激性系数越小,钉扎螺旋波消除越快.其次,障碍物大小和可激性系数影响着能成功消除钉扎螺旋波下记录反馈信号时间与加入反馈控制时间之间对应的时间间隔.最后,在保持加入反馈控制时间不变的情况下,记录反馈信号时间影响着能成功消除钉扎螺旋波所需的最小反馈控制信号幅度.
1 引言
在许多非线性反应扩散系统的斑图中,螺旋波动力系统一直受到广泛关注.螺旋波广泛存在于自然界中,例如Belousov-Zhabotinsky (BZ)反应[1]、催化表面过程[2]和心脏系统[3]等.其中,BZ 反应是最早发现螺旋波现象的自然反应系统,对BZ 反应中螺旋波的研究最早开始于20 世纪70 年代[4].在心脏系统中,螺旋电波与心动过速和危及生命的纤颤有关,它的存在会危及人体生命[5].然而,如果心脏中存在缺陷区域,螺旋波可能会被钉住,其核心将停留在缺陷区域,使它们停留的时间更长[6,7].当自由螺旋波固定在缺陷上时,就产生了所谓的钉扎螺旋波,从而导致一类生理性心律失常.因此,寻求有效的钉扎螺旋波控制方法是十分重要的.对于钉扎螺旋波,许多控制方法被研究人员提出.例如Fu 等[8]通过外部局部刺激产生靶波,然后靶波与钉住的螺旋波相互作用来消除钉扎螺旋波.Ponboonjaroenchai 等[9]提出了在给定位置进行周期性刺激产生波列控制钉扎螺旋波,研究了波列在大小和方向不同的不可激矩形障碍物上螺旋波的终止问题.Chen 等[10]研究了同步复极化能有效消除螺旋波和时空混沌.Yuan 等[11]通过边界附近的周期性扰动方法成功地解除和消除钉扎螺旋波,并且该方法对于大障碍物同样适用.
反馈法是一种控制自由螺旋波的经典方法,它具有持续时间短和反馈信号弱的优点.Yuan 等[12]利用全局反馈法消除了螺旋波和时空混沌.2017年,Hou 等[13]利用局部反馈法对螺旋波进行了控制,并且研究了反馈控制区域和位置等参数的影响.但是,现有的研究都是利用反馈法对自由螺旋波进行控制,还没有利用此方法研究钉扎螺旋波的消除.基于反馈法的优势,本文使用反馈法对钉扎螺旋波进行控制.此外,还从反馈控制信号幅度、可激性系数、障碍物的形状及大小等方面研究了反馈控制法对消除钉扎螺旋波的影响.
螺旋波的控制方程主要是反应扩散系统,学者们通常使用有限差分法研究螺旋波动力学.格子Boltzmann 方法(LBM)是一种介观数值方法,广泛应用于求解线性及非线性偏微分方程[14,15].它具有算法简单有效、计算并行、复杂边界容易处理等优点[16].本文使用格子Boltzmann 方法对Fitz-Hugh-Nagumo (FHN)模型下的钉扎螺旋波进行模拟,结合反馈法对钉扎螺旋波进行控制.
本文的结构如下: 第2 节对基于FHN 的反馈法模型进行格子Boltzmann 建模;第3 节分析模拟结果,首先研究圆形障碍和矩形障碍下钉扎螺旋波的控制情况,然后以圆形障碍物为例分别对各参数进行研究;第4 节对全文总结.
2 模 型
2.1 反馈法的格子Boltzmann 建模
FHN 模型是一种简单的双变量形式.它是对Hodgkin-Huxley 模型的简化修正[17].近年来,FHN方程已成为反应扩散系统中一种广泛应用的模型,通常用于模拟可激介质中的传播,FHN 模型也被用于模拟神经纤维和心脏组织以及化学反应中[18,19].此外,它还可用于生物学、化学、传热传质等方面的研究[20].FHN 模型的混沌性和同步性在激光技术、医学和保密通信等领域具有潜在的应用价值[21].因此,研究FHN 模型的动力学特性在实际应用中具有重要意义.FHN 模型的形式如下[11]:
其中,a和b为无量纲常数,本文固定a=0.03 和b=2.0;u为激活变量,v为抑制变量;ε为可激性系数;α 为扩散系数.
为了使用反馈法控制钉扎螺旋波,在(1)式的右侧加入反馈控制项[13]:
其中,kfb为反馈控制的幅度;Ifeedback为反馈控制项,其具体形式为
这里,D为控制的区域,t0为记录反馈信号的时间,t1为加入反馈控制的时间,t2为反馈控制结束的时间,即反馈控制持续的时间为t1—t2.
针对方程(3),可建立LBM 的演化方程[15]:
其中,hi(x,t) 表示在位置x及时间t处具有离散速度ci的粒子分布函数,τ 表示松弛时间,表示分布函数hi(x,t) 的平衡态分布函数,Gi(x,t) 为源项分布函数.
通过直接泰勒展开[16],格子Boltzmann 方法可将演化方程恢复成方程(3),具体的恢复过程可以查看附录A.
其中,ωi为权系数,满足=1 .
源项为
宏观量u(x,t) 为
对于方程(2),该方程没有扩散项,则通过有限差分法进行求解:
2.2 边界条件
以二维螺旋波为例,研究反馈法对钉扎螺旋波的控制.采用D2Q9 速度模型,速度及权重ωi大小如下:
其中,粒子速度c=∆x/∆t,∆x为空间步长.
边界的处理在数值模拟中至关重要,对采用无流边界处理的螺旋波进行研究,无流边界格式:
在使用格子Boltzmann 方法模拟螺旋波中,采用反弹格式对该宏观边界条件进行处理.反弹格式是一种启发式格子Boltzmann 方法的边界处理格式[22],包括标准反弹格式、半反弹格式和修正反弹格式.反弹格式通常被用来处理静止无滑移边界,其原理为粒子与边界碰撞后沿原路返回,具有过程简单、容易编程实现的优点.本文采用标准反弹格式进行边界处理,边界上的分布函数可表示为
其中,xb为边界格点,xf为系统内部格点,为碰撞后的分布函数,i-为i的相反方向.
2.3 模型验证
首先,对网格无关性进行验证.物理边界长度为Lx=Ly=40,选取参数ε=0.004,α=1.0 .分别选取800×800,1200×1200 和1600×1600 三种网格对模型形成自由螺旋波的过程进行模拟.该过程保持松弛时间τ 不变,选取时间步长为∆t=1/1800.图1(a)给出了在t=15时,800×800,1200×1200 和1600×1600 网格的计算情况.其中,蓝色虚线表示800×800网格下u=0.5 的等值线图,红色虚线表示1200×1200网格下u=0.5 的等值线图,蓝色实线表示1600×1600网格下u=0.5的等值线图.由图可以看出,与网格800×800 相比,1200×1200和1600×1600 网格误差较小,且在波头位置几乎重合.图1(b)描绘了在y=15时,在网格800×800,1200×1200和1600×1600 下u的变化情况.蓝色虚线、红色实线和蓝色实线分别表示800×800网格、1200×1200网格和1600×1600网格下u值情况.由图1(b)可以看出1200×1200 和1600×1600 网格结果存在一定差异,但差异较小.
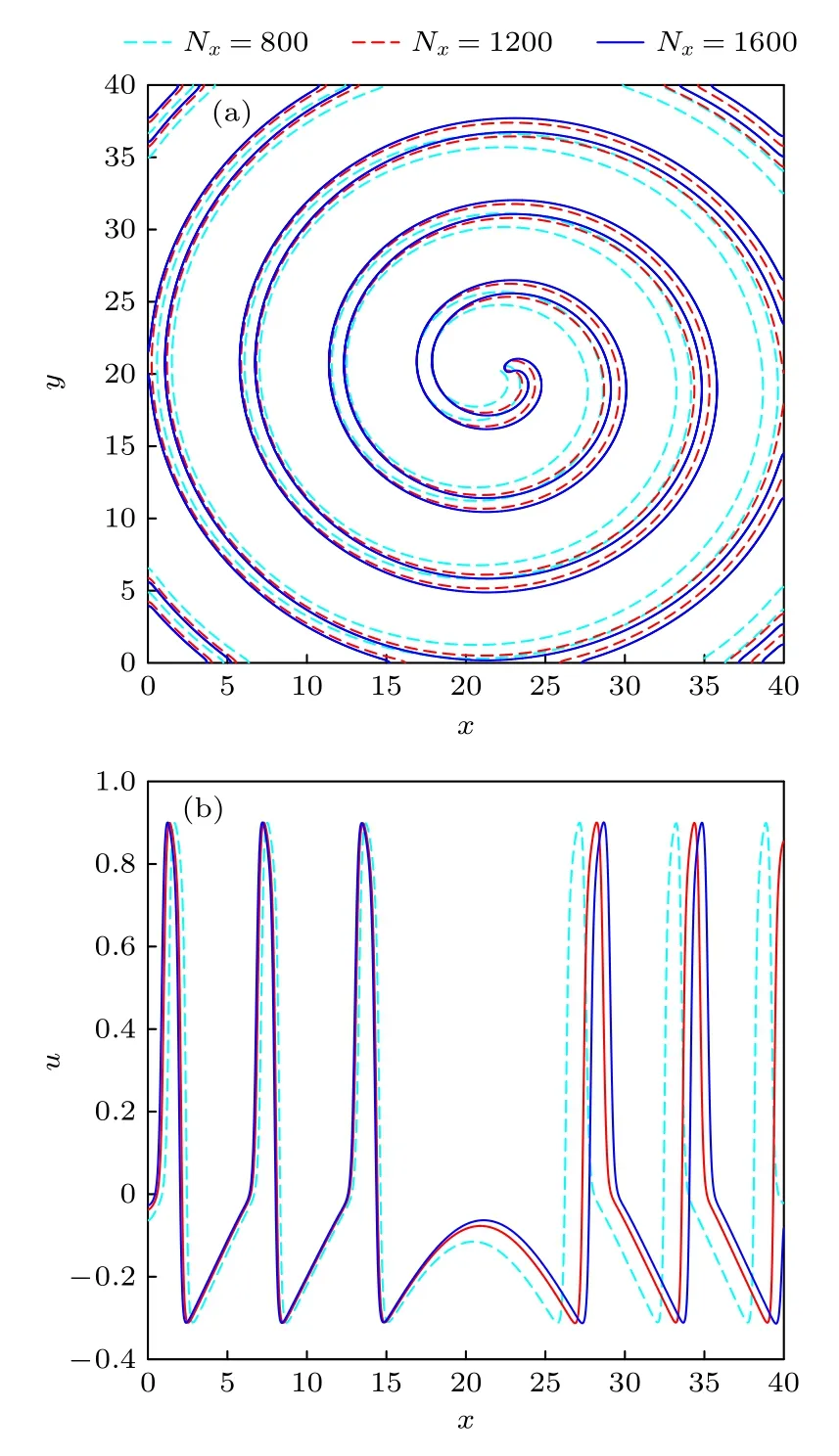
图1 (a) t=15时,u=0.5 的等值线情况;(b) t=15时,y=15处u 值情况Fig.1.(a) Contour case for u=0.5at t=15 ;(b) value of u for y=15at t=15 .
为了进一步验证网格的无关性,设定物理边界长度Lx=Ly=40,其他参数ε=0.004,α=1.0 .计算了 1200×1200 网格和 1600×1600 网格下,不同半径下钉扎螺旋波的波长情况.并根据波长情况计算出相对误差,如表1 所列.相对误差的计算公式如下:

表1 不同半径下钉扎螺旋波的波长及相对误差(1200×1200 网格和1600×1600 网格下)Table 1.Wavelengths and relative errors of pinned spiral waves at different radius (under 1200×1200 grids and 1600×1600 grids).
其中,λ 表示1200×1200网格下的波长数据,λ′表示1600×1600 网格下的波长数据.
从表1 的数据可知,在1200×1200 网格和1600×1600 网格下,半径不同钉扎螺旋波的相对误差均为 10-3量级.因此,为了提高计算效率并验证格子Bolzmann 方法的准确性,选取1200×1200网格进行后续钉扎螺旋波的模拟.下面讨论圆形障碍物下钉扎螺旋波的周期随障碍物半径的变化情况.设定物理边界长度为Lx=Ly=40,选取参数ε=0.004,α=1.0,模拟结果如图2 所示.可以看出,随着圆形障碍物半径的增加,钉扎螺旋波的周期也随之增加.与文献[11]中的结果进行对比,符合较好.
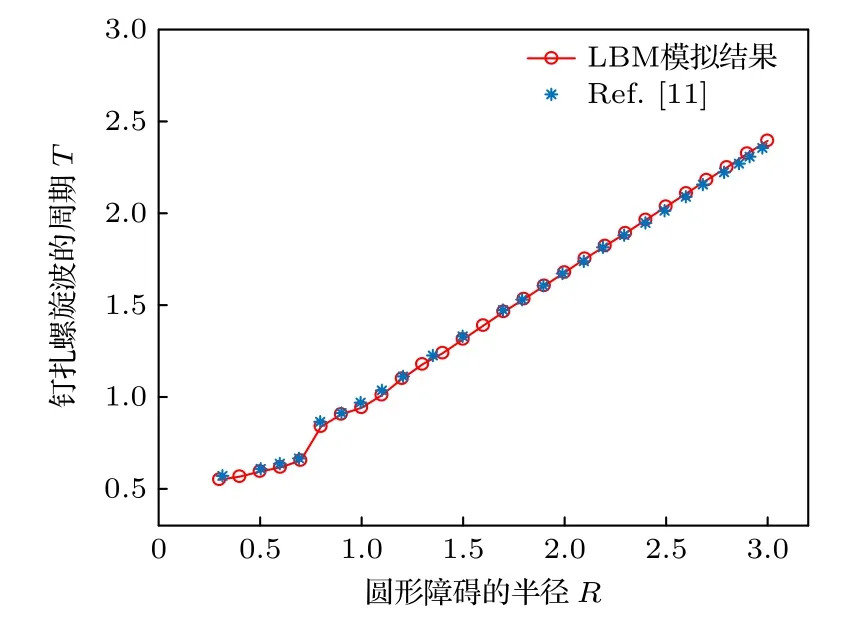
图2 与文献[11]对比,钉扎螺旋波的周期随圆形障碍物半径的变化Fig.2.Compared with Ref.[11],the period of the pinned spiral wave varies with the radius of the circular obstacle.
3 模拟结果分析
3.1 全局反馈控制
使用含反馈控制项的模型,对顺时针旋转的钉扎螺旋波进行控制.采用半径为20 的圆形边界情况进行讨论,边界条件采用无流边界.选取参数ε=0.004,α=1.0.空间步长为∆x=∆y=1/30,选取时间步长为 ∆t=1/1800 .圆形障碍物的中心位置为(20,20),障碍物半径大小为R=2.0,控制的区域D选取为整个系统.
先使钉扎螺旋波在圆形边界系统内顺时针周期旋转至少5 次.为了方便描述,以下时间t均为时间步数.图3(a)描述了点(4,20)处在加入反馈控制前不同时间步t下u的变化值,图3(b)描述了该点下u和v的关系.从图中可以看出,钉扎螺旋波在半径为2.0 的圆形障碍上进行周期运动,且通过u的最大值计算出此时钉扎螺旋波的周期为T=3020.根据钉扎螺旋波的周期,选定记录反馈信号时间t0与加入反馈控制时间t1之间时间间隔为T/6(t1-t0=T/6).如果反馈信号注入易损期的某点,该点处反馈信号会被激发.如果反馈信号注入绝对不应期的某点,该点处反馈信号不会被激发[12].故选取记录反馈信号时间为t0=19497,加入反馈控制时间为t1=20001,反馈控制结束时间为t2=20090 .
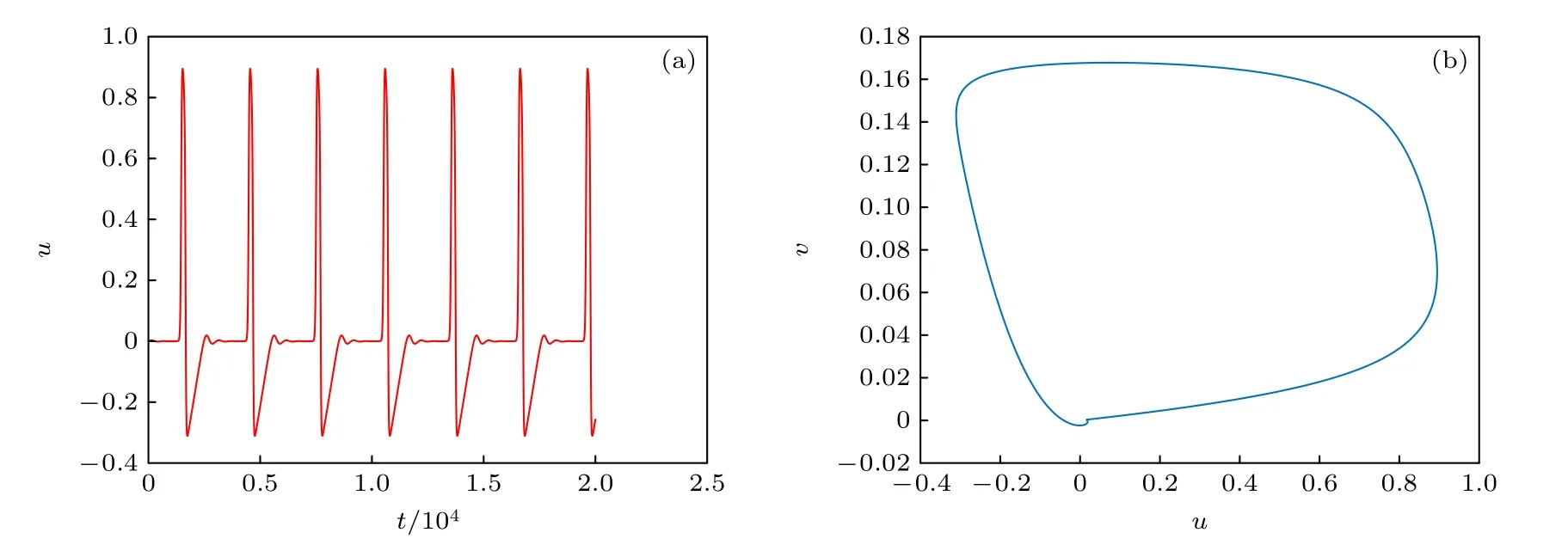
图3 在点(4,20)处u 和v 的值(a) u 与时间步t 的关系;(b) u 和v 的相图Fig.3.Values of u and v at the point (4,20): (a) Relationship between u and the time step t;(b) phase diagram of u and v.
图4 给出了kfb=0.5下,使用LBM 模拟圆形障碍下钉扎螺旋波的控制情况.首先,钉扎螺旋波S1在系统内顺时针旋转,如图4(a)所示.t=20001时间步时加入反馈控制,如图4(b)所示.由于系统内部分点处于易损期,会使系统内激发形成第二个钉扎螺旋波S2,且S2的波宽会经历逐渐增大后减小的过程,如图4(c)—(f)所示.随后,钉扎螺旋波S1顺时针旋转,而钉扎螺旋波S2逆时针旋转.当两个波阵面相遇时,根据激发态波的特性,激发态会碰撞消失,没有进行湮灭的残余部分形成激发态S3,如图4(g)—(j)所示.此时,系统内没有点缺陷行为,不会形成新的螺旋波.当S3被逐出系统时,系统恢复静息态,如图4(k)—(l)所示.

图4 利用反馈法控制圆形障碍物下钉扎螺旋波的情况Fig.4.Suppression of a pinned spiral wave under a circular obstacle by feedback control approach.
为了更加方便地描述反馈法对钉扎螺旋波的控制效果及控制时间,采用以下形式来描述系统的行为:
其中,u(x,y) 为系统内全局的快变量u的值.当uall≤10-4时,认为系统恢复了静息状态.
图5 给出了上述圆形障碍物下钉扎螺旋波控制过程中uall的变化情况,从加入反馈控制时间t1开始记录uall.从uall的变化过程可以看出,uall的第一个小高峰值为控制结束时间t2,uall的第二个高峰值为钉扎螺旋波S2的波宽达到最宽时的状态.注入反馈信号的1100 个时间单位后,此时uall≤10-4,系统内的钉扎螺旋波被完全消除,小于一个激发态周期.

图5 ε=0.004, R=20, kfb=0.5 下反馈法控制钉扎螺旋波过程中 uall 的变化值Fig.5.Change of uall of unpinning spiral waves with ε=0.004, R=20, kfb=0.5.
接下来,为了讨论反馈控制法下障碍物形状的无关性,考虑矩形障碍物下钉扎螺旋波的控制情况.采用半径为20 的圆形边界情况进行讨论,边界条件采用无流边界.选取参数ε=0.004,α=1.0.空间步长为∆x=∆y=1/30 .选取时间步长为∆t=1/1800.正方形障碍物的中心位置为(20,20),障碍物边长为L=4.0 .由数值模拟可知,钉扎螺旋波在正方形障碍边长为4.0 时的周期为T=3621,则选定t0与t1之间时间间隔约为T/6 .因此,选取t0=19397,t1=20001,t2=20090 .
图6 给出了kfb=0.5时,使用LBM 模拟正方形障碍下钉扎螺旋波的控制情况,可以发现方形障碍下利用反馈法控制钉扎螺旋波的情况跟圆形障碍下的控制情况类似.钉扎螺旋波S1在系统内绕着正方形障碍物顺时针旋转,加入反馈控制后,系统内形成第二个钉扎螺旋波S1,见图6(a),(b).钉扎螺旋波S2会被系统激发成可激状态,其波宽逐渐增大后减小,如图6(c)—(f)所示.随后,钉扎螺旋波S2绕着正方形障碍物顺时针旋转,而钉扎螺旋波S1绕着正方形障碍物逆时针旋转,直到两者相遇形成激发态S3,如图6(g)—(j)所示.随着S3被逐出系统,系统恢复静息态,见图6(k)—(l).

图6 利用反馈法控制正方形障碍物下钉扎螺旋波的情况Fig.6.Suppression of a pinned spiral wave under a square obstacle by feedback control approach.
3.2 参数对钉扎螺旋波控制的影响
本节以圆形障碍物为例,考虑控制系统中各参数对钉扎螺旋波控制的影响.从(3)式可以看出,反馈控制的幅度kfb、可激性系数ε和记录反馈信号时间t0对反馈控制有影响.此外,还将讨论障碍物大小对钉扎螺旋波控制的影响.
3.2.1 反馈控制的幅度kfb
kfb的大小是反馈控制的关键因素,其取值一般介于0—1 之间.对于心脏系统来说,若kfb取值过大,则对系统损伤严重.取定扩散系数α=1.0,可激性系数ε=0.004,圆形障碍半径R=2.0,在0—1 范围内均匀增大kfb,考虑不同kfb下消除钉扎螺旋波的时间,如图7 所示.从图中可以看出钉扎螺旋波的控制时间随着kfb的增大而减小.当kfb越大时,注入系统内反馈项的值越大,被激发成新的钉扎螺旋波所需的时间越少,因此影响钉扎螺旋波的控制时间.
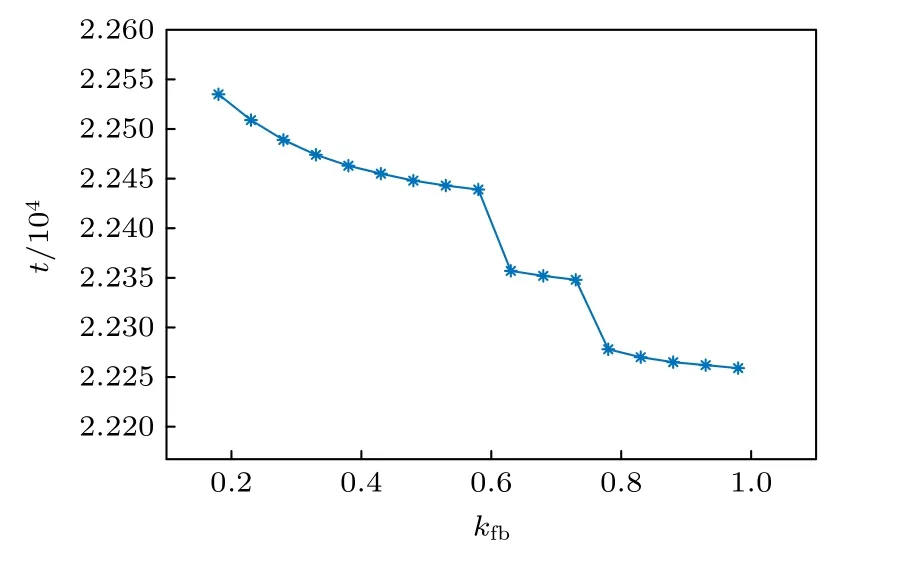
图7 不同 kfb 下消除钉扎螺旋波的时间步Fig.7.Time step of unpinning spiral wave with different .
3.2.2 可激性系数ε
可激性系数ε影响着钉扎螺旋波的动力学行为.接下来,考虑在不同的可激性系数ε下钉扎螺旋波的控制情况.控制扩散系数α=1.0,圆形障碍半径R=2.0不变,讨论能使不同的可激性系数ε下钉扎螺旋波得到控制的kfb最小值,这里用kfbmin来表示.加入反馈控制时间t1=20000,反馈控制结束时间t2=20090.图8(a)记录了不同ε下,钉扎螺旋波的周期T.根据不同ε下的周期T,选取记录反馈信号时间t0,使其与t1之间的时间间隔为T/10,如图8(b)所示.图8(c)描绘了能成功控制钉扎螺旋波所需的kfbmin.可以看出kfbmin随着可激性系数ε的增大呈现先减小后增大的现象.在保持kfb=0.5 的情况下,讨论了不同可激性系数ε下的控制时间,如图8(d)所示.反馈法下钉扎螺旋波的控制时间随着可激性参数的增大而增大.

图8 (a)钉扎螺旋波的周期随可激性系数 ε 的变化;(b)记录反馈信号时间 t0 随可激性系数 ε 的变化;(c) kfbmin 随可激性系数ε的变化;(d)钉扎螺旋波的控制时间t 随可激性系数 ε 的变化Fig.8.(a) Variation of the period of the pinned spiral wave with ε ;(b) variation of the time of recording the feedback signal with ε ;(c) variation of kfbmin with ε ;(d) variation of the time required to eliminate the pinned spiral wave with ε .
此外,还讨论了在不同的可激性系数ε下能够成功控制钉扎螺旋波的记录反馈信号时间t0与加入反馈控制时间t1之间时间间隔的范围.在其余系统参数不变的情况下,钉扎螺旋波的周期跟障碍物的周长有关.并将该时间间隔与钉扎螺旋波的周期进行换算(例如,若t0与t1之间的时间间隔为60,某参数下钉扎螺旋波周期为600,则该时间间隔为周期的1/10).为了方便观察记录,将不同ε下的t1都选取为钉扎螺旋波的可激态刚好运动到圆形障碍物的正上方(即圆形障碍物的十二点钟方向),并以T/360 为时间间隔进行讨论,其中T为钉扎螺旋波的周期.从图9 可以看出,随着ε的增大,t0与t1之间时间间隔的范围减小,这是由加入反馈信号时系统是否处于易损期决定的.并且在不同的ε下,t0与t1之间时间间隔最小均可为T/360,即当t0与t1之间的时间间隔为相应钉扎螺旋波周期的1/360时,也能成功消除钉扎螺旋波.

图9 不同 ε下,能够成功控制钉扎螺旋波的记录反馈信号时间 t0 与加入反馈控制时间 t1 之间时间间隔对应的范围Fig.9.Corresponding range of the time interval between the recording feedback signal time t0 and the adding feedback control time t1 with different ε .
3.2.3 记录反馈信号时间t0及圆形障碍物半径
由前面的讨论可知,在不同的可激性系数ε下,能够成功控制钉扎螺旋波的记录反馈信号时间t0与加入反馈控制时间t1之间都有对应的一个时间间隔.若保持ε及t1不变,在对应的时间间隔内讨论t0,则可以得到不同t0下能成功控制钉扎螺旋波的情况.控制变量不变,保持t0持续变化,讨论不同t0下能够成功控制钉扎螺旋波所需的最小的kfb,如图10 所示.kfbmin随着t0的增大呈现先减小后增大的情况,这与文献[13]反馈法控制自由螺旋波的情况一致.圆形障碍物的大小对使用反馈法控制螺旋波也有重要的影响.图11 给出了不同半径下能够成功控制钉扎螺旋波的记录反馈信号时间t0与加入反馈控制时间t1之间对应的时间间隔.随着圆形障碍半径R的增大,t0与t1之间时间间隔的范围减小.这是由加入反馈信号时系统是否处于易损期决定的.并且R不同时,能成功控制钉扎螺旋波下t0与t1之间时间间隔最小均可为T/360 .
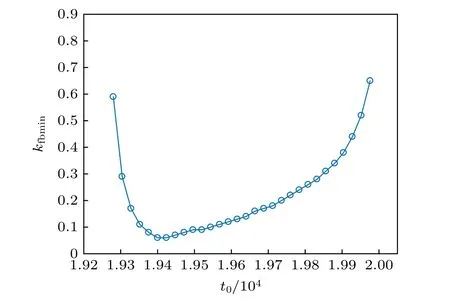
图10 在不同的t0下,能 成功控制钉扎螺 旋波所需的kfbmin 的变化情况Fig.10.Change of kfbmin of unpinning spiral wave successfully with different t0 .

图11 不同R下,能够成功控制钉扎螺旋波的记录反馈信号时间 t0 与加入反馈控制时间 t1 之间时间间隔对应的范围Fig.11.Corresponding range of the time interval between the recording feedback signal time t0 and the adding feedback control time t1 with different R.
4 结论
本文利用反馈控制法研究了钉扎螺旋波的消除情况,并研究了反馈控制中参数的影响.模拟结果表明,反馈法能够有效控制钉扎螺旋波.首先,分别在圆形障碍物和矩形障碍物下验证了反馈法对于钉扎螺旋波消除的有效性.其次,研究了反馈控制信号幅度和可激性系数对控制钉扎螺旋波的影响,并研究记录了能够成功控制钉扎螺旋波的记录反馈信号时间与加入反馈控制时间之间对应的时间间隔.可以发现钉扎螺旋波的控制时间随着反馈控制信号幅度的增大而减小.而钉扎螺旋波的控制时间随着可激性系数的增大而增大,这是由于可激性系数增大时,螺旋波的波宽随之减小,从而影响控制时间.最后,研究了圆形障碍的半径和记录信号时间的影响.在不同的记录信号时间下,能成功消除钉扎螺旋波的最小反馈控制信号幅度不同,呈现先减小后增大的趋势.基于本文的讨论可知,反馈法对于自由螺旋波和钉扎螺旋波都具有很好的控制作用.基于该方法具有反馈信号弱和反馈持续时间短的优点,对该方法进一步研究,可以大幅度提高控制螺旋波的效果.
附录A
在本附录中,采用直接泰勒展开(DTE)从现有的格子Boltzmann 模型中恢复带有反馈控制项的FHN 模型.对方程(5)进行泰勒展开,可以得到:
由(A2)式可以得到:
将(A4)式代入(A3)式,有
为了恢复正确的带有反馈控制项的FHN 模型,分布函数hi,和Gi满足以下条件:
通过上述关系,对具有O(∆t)和O(∆t2) 阶的(A2)式和(A5)式求零阶矩,可得:
将(A10)式代入(A9)式即可恢复宏观方程(3),且α=(τ-1/2).
