量子信息中的度量空间方法在准周期系统中的应用*
2024-03-19冯曦曦陈文高先龙
冯曦曦 陈文 高先龙‡
1) (浙江师范大学物理系,金华 321004)
2) (北京计算科学研究中心,北京 100193)
得益于量子信息理论的发展,保真度、纠缠熵等概念被引入到量子相变的研究中,不仅能用来标识新奇的物质相,还能用来探测量子相变的临界点以及描绘其临界行为.从度量空间的角度来看,这些物理量都可以被理解为度量空间中两个函数的距离.本文利用波函数和实空间中密度分布函数的距离,研究了以广义Aubry-André-Harper 模型为代表的准周期系统,发现该方法不仅能标识拓展相、临界相和局域相,还能找到准确的相变点并计算出临界指数.此外,不仅将度量空间方法推广到波包扩散动力学研究,还提出了一种新的量,即态密度分布函数的距离,发现上述定义的两种物理量都能标识不同的物质相及相变点.通过定义某个函数在不同参数下的距离,不仅为标识已知系统相变点提供了研究工具,还为探测未知系统的不同物质相、相变点及其临界行为提供了一种直观的方法.
1 引言
与经典相变主要由热涨落主导的特点不同,量子相变是指通过改变非热控制参数触发体系的基态性质在临界点上的突变[1,2].随着拓扑相变、多体局域化、动力学相变等概念的出现,如何理解这些新奇物质相的性质,用合适的可观测量去标识不同的物质相及相变点,描绘体系在相变点附近的临界行为成为一个重要课题,并引起了广大研究者的兴趣.得益于量子信息理论的发展,保真度[1,3–5]、纠缠熵[6,7]、Fisher 信息熵[8–12]、错时序关联 (out of time ordered correlation,OTOC)函数[13–15]等物理量被引入到量子相变的研究中,不仅在理论和数值模拟中成功标识了体系的相变点、临界指数及其普适类,还在实验中得到验证和应用.
上述量子信息中的概念,在数学上可以看作不同的波函数或密度分布函数在希尔伯特空间中的距离,是对某两个波函数或密度分布函数差异化的度量.希尔伯特空间作为量子态存在的空间,不仅是一个内积空间,同时还是一个度量空间,可以定义不同矢量间的距离.D’Amico 等[16–18]引入度量空间方法,提出了计算不同参数下体系的基态波函数和密度分布函数的距离,继而发现在一些情形中二者是近线性映射关系.他们不仅用该方法发展了密度泛函理论,还用来度量量子非平衡动力学系统的绝热程度[19].至此,我们还可以提出一些开放性的问题.例如,是否可以用上述的两种距离去度量量子相变,能否标识不同的物质相、相变点以及描绘相变点附近的临界行为,进而求解出临界指数?是否可以得到与保真度、纠缠熵等量子信息中的物理量相同的结果? 除了上述两个距离,是否还能定义不同的距离量?譬如不同非热控制参数下体系的态密度分布函数,是否可以用来标识相变? 本文以广义Aubry-André-Harper (AAH)模型为例,试图回答上述问题.
广义AAH 模型是一类具有准无序项的紧束缚格点模型.对于一维无相互作用的含有准无序势和最近邻跃迁项的AAH 模型,可以看作将一维安德森无序模型的随机势替换成准无序势.相比于安德森无序模型在一维、二维情况下没有相变,该模型在一维情形下,即可观测到随着准无序外势的变化体系呈现波函数的拓展——安德森局域相变,且在相变点上波函数和能谱呈现出奇异的分形结构[20–22].随着理论上对其拓展情况——广义AAH 模型研究的深入,包括引入非厄米项、多体相互作用项、长程跃迁项、p波配对项研究其能谱的实-复转变、拓扑相变等[23–28],以及其在冷原子[26,29,30]、光晶格[31–34]、超导量子比特平台[35,36]的实验实现,广义AAH 模型成为了理解安德森局域化、多体局域化的重要平台.本文将量子信息中的度量空间方法引入到广义AAH 模型中,讨论波函数的距离、度量空间的距离是否能够标识广义AAH 模型中丰富的物质相,并且试图将波函数的度量空间方法推广到态密度分布函数的度量空间中去.
本文的结构如下: 第2 节介绍度量空间及距离等相关概念,讨论常见的度量空间中的距离和系统间波函数性质之间的关系,同时给出广义AAH 模型;第3 节将度量空间方法应用到准周期系统中,成功标识不同的物质相、相变点及临界指数;第4 节将度量空间方法中的波函数、密度分布距离推广到动力学距离和态密度距离,并应用到准周期系统中去;第5 节总结结果并展望.
2 度量空间和模型
度量空间由一个非空集X和一个度量(距离)函数D组成,记作(X,D).在一个度量空间中,集合X中的元素被称为点,而度量或距离函数D定义了点之间的距离.度量函数D满足以下性质:
其中x,y,z为集合X中的元素.最典型的距离是欧几里得距离,广义的欧几里得距离定义为
当p=2,即我们熟悉的欧几里得距离的定义.在量子力学中,用以表征系统状态的波函数通常可以构成一个希尔伯特空间——完备的内积空间.希尔伯特空间在数学上结合了向量空间和度量空间这两种不同类型空间的性质.具体来说,希尔伯特空间作为一个向量空间,满足向量的线性组合和加法运算的性质,可以描述向量间的线性关系,进行向量的加法、数乘等运算.同时,希尔伯特空间也是一个度量空间,它具有度量的概念.通过引入一个合适的度量,可以定义度量空间中的波函数ψ的距离函数[18].
这个距离函数可以衡量两个波函数之间的相似程度.对于具有N个粒子的量子体系,当该度量的值为时,表示它们在空间中正交或完全不相似;当度量为0时,则代表两者完全相同.利用同样的方法,可以在度量空间中定义出任意两个密度分布函数ρ之间的距离函数[18]:
对于具有N个粒子的量子体系,当该度量接近2N时,表示这两个体系下的密度分布完全不相似;当度量接近0时,则代表两者非常相似.
本文把度量空间应用于具有非公度非对角调制的一维广义AAH 模型,其哈密顿量为
其中L为晶格长度,为硬核玻色子的产生(湮灭)算符.Jn和λn分别为最近邻跃迁和在位势,它们的表达式分别为
其中无理数α=(-1)/2,δ和λ分别为非对角无序势强度和对角无序势强度.ϕ1和ϕ2为两个相位,它们的取值范围是0— 2π .在本文中,考虑周期性边界条件.
当δ=0时,该模型等价于AAH 模型.该模型拓展到局域的转变点是λ/J=2,当λ/J<2时,所有的本征态弥散在整个实空间中,称为拓展态;当λ/J>2时,所有的本征态都局域在实空间中的一点,称为局域态.当δ≠0时,该模型可称为广义AAH 模型,包含对角调制和非对角调制.在保持其他参数不变的情况下,仅通过改变ϕ1的值,就可以引起拓展-局域、拓展-临界转变相边界的改变[37].不失一般性,本文选取ϕ1=(-1)π/2,处在该相位的系统提供了一个较大的临界区,这为研究拓展-临界的转变提供了良好的平台.此外,本文将设J=1 作为能量单位.
通常用于描述系统局域-拓展性质的量为逆参与率 (inverse participation ratio,IPR):
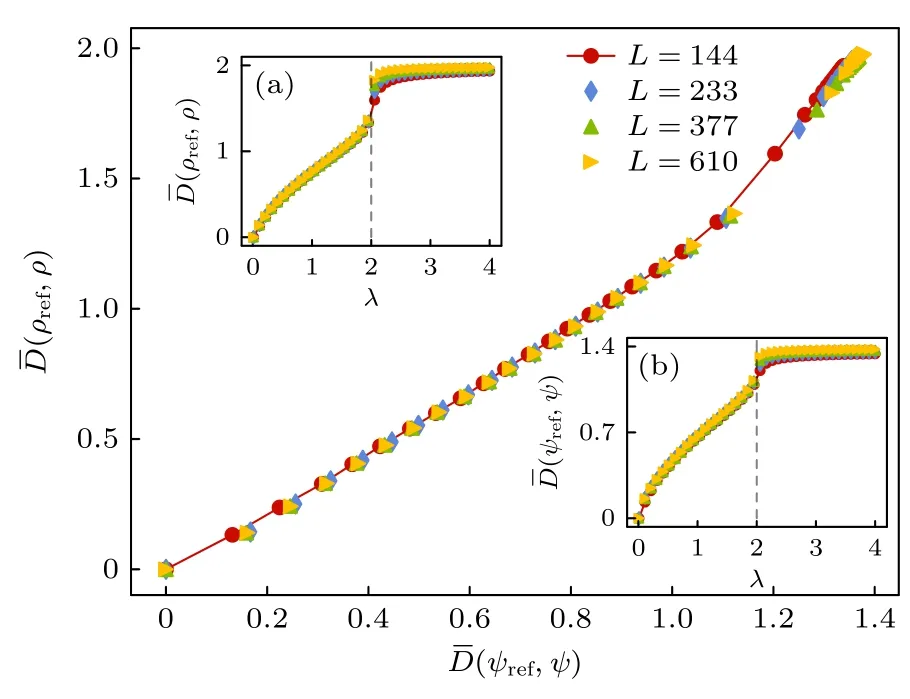
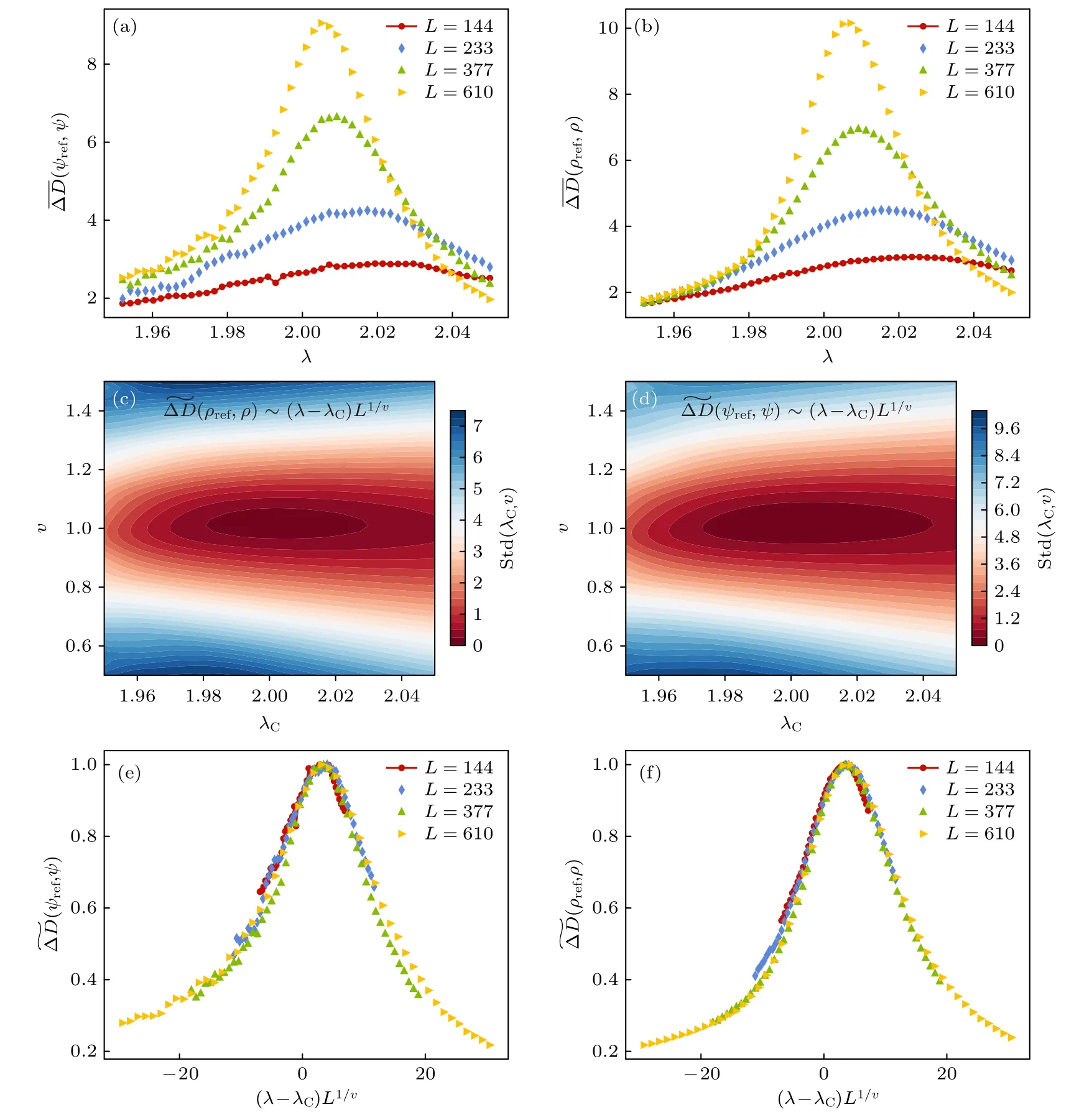
这里,n代表第n个格点,ψj代表系统的第j个本征态.在热力学极限下,即L →∞,如果一个态是拓展的,容易验证其IPR→0 ;若这个态是局域的,则IPR→1.当0 除此之外,由内积运算定义的用于衡量两个波函数相似程度的保真度: 也被证实为一种有效的研究准周期系统的量[2-5],它同样也与距离的定义有联系: 为了探究AAH 模型中拓展-局域相变,探索了波函数距离和密度距离随着无序强度λ的变化.参考点的选择是十分重要的,它衡量待测系统与给定的参考系统之间的差距.由于这里考虑的是拓展-局域相变,一个十分自然的选择是以拓展相为参考系统,从而衡量随着参数的变化系统发生的相变行为.首先考虑一个处于拓展态的系统为参考系统,参数选择λ=0.01,δ=0,以该系统的各个本征态为参考态.从而进一步给出平均波函数距离(ψref,ψ)和平均密度距离(ρref,ρ) : 其中,j代表第j个本征态. D’Amico 等[16–19]在多种模型的数值研究中发现,基态波函数和密度之间的霍恩贝格-科恩映射(Hohenberg-Kohn mapping)可推广到度量空间中,即波函数距离和密度距离之间存在近线性映射关系.那么,该结论在无序体系中是否依旧成立?此处,以和为物理量探求该问题的答案.如图1 主图所示,和大体上仍呈近线性映射关系,但在=1.0处两者之间存在一定的偏离.该偏离源自于这两个物理量平均了激发态的信息,而激发态波函数距离和密度距离之间存在更复杂的映射关系.但激发态的复杂性总体上仍然保持了平均波函数距离和密度距离间的一一映射关系.因此无序体系中的霍恩贝格-科恩映射也可推广到度量空间中,即密度距离和相关波函数距离之间的映射仍然是可逆的. 图1 不同尺寸下平均波函数距离随平均密度距离的变化.插图(a),(b)的横坐标皆为无序强度 λ,纵坐标分别为平均密度距离和平均波函数距离.不同颜色的线代表不同尺寸下的结果,无序平均次数取为50Fig.1.Variation of average wave function distance with the average density distance.Abscissa of panels (a) and (b) are the disorder intensity λ,and the ordinates are the average density distance and average wave function distance,respectively.Color bar represents the result under different size,and the disorder realizations are 50. 除了映射关系,我们更关心在度量空间中是否也能显示出量子相变并给出相变点.如图1(a)所示,当λ<2,即系统处于拓展相时,平均密度距离随着λ的增加而增加.这说明尽管λ<2,由无序强度控制相变的准周期系统都处于拓展相,但是平均密度距离显示出在度量空间中拓展相与拓展相仍是不尽相同的.因此想要通过这个量去判断系统是否产生相变,并不能简单地由距离的大小去判断.当λ=2 时平均密度距离产生了一个跃变行为,这与之前近线性的增长行为不一致,说明λ=2 是发生相变的一个临界点.当λ>2,平均密度距离逐渐趋于最大值 2,并维持该值不变,这意味着体系此时处于局域相.图1(b)展示的是平均波函数距离随着无序势强度λ的变化,与平均密度距离具有类似的行为,同样可以得到临界点λ=2 . 以上是利用度量空间中的平均波函数距离和密度距离的变化规律对相变点做出了判断,进一步,一阶平均波函数距离和密度距离的有限尺寸分析为这一判断提供了更强有力的说明.令人惊喜的是,它不仅能够定位出一维AAH 模型相变点,还能提取出该模型的相变点的关联长度临界指数.一阶平均波函数距离被定义为 同理,可以得到一阶平均密度距离: 如图2(a)和图2(b)所示,不同晶格尺寸(L=144,233,377,610)下,一维AAH 模型的一阶平均波函数距离和密度距离作为无序强度λ的函数,其最大值总是位于λ=2 附近.这说明在该点系统的物质相产生了剧烈的变化,为该模型的相变点.出现这一现象的原因与保真磁化率在相变点处的变化是相同的[3].假设标度方程为 图2 一维AAH 模型中一阶平均波函数距离和密度距离的有限尺度分析(a),(b)不同尺寸下一阶平均波函数距离和密度距离随无序强度 λ 的变化;(c),(d)不同拟合参数下,有限尺寸分析的误差Std(λC,v),颜色棒的深浅为误差的大小;(e),(f)缩放一阶平均波函数距离及缩放一阶平均密度距离作为缩放变量(λ-λC)L1/v 的函数.无序平均次数为50 次Fig.2.Finite scale analysis of the first-order average wave function distance and density distance in the one-dimensional AAH model: (a),(b) Variation of first-order average wave function distance and density distance with disordered intensity λ under different sizes;(c),(d) error of finite size analysis under different fitting parameters Std(λC,v) .Color bar represents the value of the error;(e),(f) scaling of the first-order average wave function distance and the first-order average density distance as a function of the scaling variable(λ-λC)L1/v .The disorder realizations are 50. 由此可得,不同尺寸下的一阶平均波函数距离和密度距离的曲线应当塌缩至同一条理论曲线上. 通过上述的分析可知,在度量空间中拓展相与拓展相之间仍存在差异,拓展相与局域相之间的差异则基本恒定,且趋于其在空间中的最大值.那么拓展相与临界相之间的差异又如何? 广义AAH 模型为利用度量空间的概念去研究拓展-临界相变提供了良好的研究平台.同样,以λ=0.01,δ=0 为参考系统,由于在之前的分析中,波函数距离和密度距离两者的表现结果基本相同,此处仅给出密度距离与λ和δ的关系.如图3 所示,横坐标为非对角无序势δ,纵坐标为对角无序势λ.当λ<2,δ<1时,D(ρref,ρ)<1.2,即绿色区,体系处于拓展相;当δ>1,λ>2δ时,D(ρref,ρ)≈2,即蓝色区,体系处于局域相.除此之外的区域,体系都处于临界相.该区域的色块并非同一,D(ρref,ρ) 的值介于1.2—1.84之间但没有达到最大值 2,这说明临界相与拓展相具有一定的相似性.由于临界相与临界相之间也不全是相同的,所以选定拓展相为参考态时,在临界区呈现出了少部分不一致的区块.至于不同的临界相之间具体有什么区别,会带来什么不同的现象,仍需要用除度量空间外的方法进一步研究.利用密度距离给出的相图与文献[37]给出的IPR 相图一致,这说明从度量空间角度分析量子系统的相变现象是一种有效的方法. 图3 广义AAH 模型的相图.颜色的深浅代表(ρref,ρ)的大小,这里选择 L=610 .绿色区域A 为拓展相,橙色区域B 为临界相,蓝色区域C 为局域相.无序平均的次数取为50 次Fig.3.Phase diagram of the extended AAH model.Color bar represents the value of (ρref,ρ),calculated for chains of length L=610 .Green region A represents the extended phase,the orange region B represents the critical phase,and the blue region C represents the localized phase.Disorder realizations are 50. 度量空间这一概念具有广泛的适用性,本节将其应用到波包扩散的动力学和系统的能谱性质研究中,以期在度量空间中获得更多关于系统的信息.一是通过动力学波函数距离和密度距离探索不同的物质相对系统的演化速率的影响;二是通过定义新的物理量——态密度距离,探求不同物质相之间能谱的差距.令人惊喜的是,这两种推广方法同样能够揭示量子相变的存在,为我们提供了更丰富的分析手段和视角,进而更全面地分析和解释系统中的特性变化.在以下研究中,仅验证图3 中横轴(λ=0)和纵轴(δ=0)所展现的两种相变情况. 由于处于不同相的系统具有不同的动力学行为,因此在度量空间中观察系统的动力学演化也为量子相变的研究提供了一种新思路.下面基于AAH 模型和广义AAH 模型,讨论拓展、临界和局域三种不同相下密度距离的动力学演化行为.在该研究中,选择粒子以相同概率分布在各个格点的理想情况下的拓展态为参考态,其中 |cn|2≡1/L,|n〉 代表粒子位于第n个格点处的占据态.假设在t=0时,粒子局域于x0=L/2格点处,那么 |ψ(0)〉=|x0〉,|ψ(0)〉 即为选定的初态.t时刻的波函数可表示为 |ψ(t)〉=可以得到ρref=|ψref〉〈ψref|,ρ(t)=|ψ(t)〉〈ψ(t)| .由方程(6)即可得动力学密度距离: 动力学波函数距离D(ψref,ψ(t)) 也可用相同的方法得到.由于波函数距离和密度距离之间具有一一映射关系,下文仅展示动力学密度距离的结果. 由图3 的相图可知,当δ=0,随着λ的增加,体系在λ=2 处发生拓展-局域转变.如图4(a)所示,选择δ=0,λ ∈(0,4) 的参数范围,从下至上无序强度λ逐渐增加.在蓝线区域D(ρref,ρ(t)) 随着t的增加而减小.在t=0时,体系尚未开始演化,此时体系处于局域态,与参考态间存在巨大的差异,因此动力学密度距离呈现最大值2.但随着体系的演化,动力学密度距离的值下降.这是因为系统逐渐演化至拓展相,体系与参考态所处的相逐渐接近,两者的距离不断减小.而在红线处D(ρref,ρ(t))的值一直在2 附近振荡,这代表此时体系与参考态的距离最大,体系没有产生较大的变化,仍处于局域相.从蓝线到红线的变化,展现了拓展-局域转变,这与定态情况下无序强度λ控制AAH 模型产生相变的规律是一致的.正如前文所言,广义AAH模型为研究拓展-临界相变提供了便利.同样,由图3 可知,当λ=0,随δ的增长体系在δ/J=1 处发生拓展-临界转变.选择λ=0,δ ∈(0,4) 的参数范围,在该条线上展现了动力学密度距离随拓展-临界转变的变化.图4(b)密度距离的动力学演化看似与图4(a)一致,但仍然存在差异.首先是D(ρref,ρ)只有少数几条粉色线的值趋于2,而大多数红色线的密度距离的值是介于1.75—2 之间的.这说明在δ处于一个较大值时,体系并非为局域相,而是稳定在了一个拓展与局域之间的相,即临界相.其次是图4(a)与图4(b)中蓝线的疏密程度不同,图4(b)中的线条明显比图4(a)稀疏,这说明拓展-临界产生相变点的位置早于拓展-局域产生相变的位置. 为了进一步从密度距离的动力学行为中得到明确的相变点,首先给定了动力学密度距离D(ρref,ρ(t))随时间t变化快慢的幂律关系: 并在图4(c)和图4(d)中分别展示了γ作为λ和δ的函数的变化.在图4(c)中,不同尺寸下都具有相似的行 为,即随着λ的增加 |γ| 逐渐增加,并在λ=2减小至0 不再变化.这个过程明显展现了拓展到局域的转变,并给出了相变点.同样可以得到γ与δ的关系,如图4(d)所示.在δ=1 处,γ稳定于一个略小于0 的值,尺寸越大效果越明显,这说明在δ=1 处产生了拓展-临界相变. 上述内容显示,波函数距离和密度距离两种度量在静力学和动力学研究中均可用于找到量子相变点,这启发我们将该度量函数推广至态密度分布函数g(E), 其中,Ei为约化能量: 式中ε为系统的本征能量.以λ=0.01,δ=0 为参考系统,如图5(a)所示,蓝线为δ=0,态密度距离随λ的变化曲线.态密度距离随着λ的增大,经历了一个先增加再减小的变化,在临界点λ=2 处达到最大值,态密度距离的这种变化代表了拓展-局域转变.由此可以推测出即便从波函数的角度来看,处于拓展相的系统与临界相的系统之间的差异并不特别明显,而是与处于局域相的系统之间的差异性最大.但从能谱的角度来看,反而是处于拓展相的系统与局域相的系统之间比较接近,而与处于临界相的系统具有较大的差异.图5(a)中的红线进一步说明了拓展相的能谱与临界相的能谱间具有较大的差距.红线展现的是当λ=0,态密度距离随δ的变化.在该参数范围内,随着δ的增大,态密度距离先增大并在δ=1 处趋于一个饱和值,体系经历了拓展临界相变,相变即为δ=1 .这与3.2 节及4.1 节中的结论是一致的.为了易于理解,图5(b)给出了不同相的态密度分布图像.红线、蓝线、绿线分别代表拓展态、临界态和局域态的约化态密度图.从图中能够很直观地看出,临界态的态密度与其他两个相具有非常大的不同.临界相的能谱具有丰富的分型结构,这可能是导致其与其他相的态密度距离相差巨大的原因,而这种特殊的结构能够从态密度距离中体现出来. 图5 态密度距离图(a)在L=610下,以 λ=0.01, δ=0为参考系统的态密度距离随参数的变化.红线为当 λ=0,态密度距离随参数 δ 的变化.蓝线为当 δ=0,态密度距离随参数 λ 的变化.(b)以基态为零能点,当 δ=0 ,λ=1.0,2.0,4.0,即红线、蓝线、绿线,分别代表拓展态、临界态和局域态的约化态密度图.无序平均次数为50 次Fig.5.Density of state distance: (a) At L=610,density of state distance of the reference system varies with parameters λ and δ .The red line represents the variation of the density-of-state distance with parameter δ when λ=0 .The blue line represents the variation of the density of state distance with parameter λ when δ=0 .(b) Reduced density of states by taking the ground state as the zero-energy point.δ=0 ,λ=1.0,2.0,4.0,namely,the red line,blue line,and green line,respectively,represent the extended state,critical state,and localized state.The disorder realizations are 50. 本文介绍了度量空间中的距离的概念,用这一概念理解了IPR 和保真度,并且用波函数距离和密度分布函数距离研究了广义AAH 模型的相图,发现不仅可以标识不同的物质相,给出准确的相变点,还能计算出与其他文献相符的临界指数.在此基础上,将距离推广到波包扩散动力学和态密度分布函数距离中,都得到了一致的结果.这一研究不仅有助于理解现有的物理量,同时提供了一种直观的探测新奇物质态的方式——直接比较系统在不同非热参数下的本征态、密度分布、态密度分布函数的差异,找到不同的物质相和准确的相变点,并描绘其临界行为.距离这一概念同样也易推广到其他物理量中,通过比较物理量间的距离变化与波函数、能谱的距离变化,或许能够帮助我们找出波函数或能谱对系统性质的不同影响.此外由于其简单、直观和易推广的特点,这些概念有望在实验中得到应用.3 度量空间方法在量子相变中的应用
3.1 拓展-局域相变的研究
3.2 拓展-临界相变的研究

4 动力学距离和态密度距离
4.1 动力学距离
4.2 态密度距离

5 总结与展望
