一维超冷原子动量光晶格中的手征对称性破缺拓扑相*
2024-03-19曾超毛一屹吴骥宙苑涛戴汉宁陈宇翱
曾超 毛一屹 吴骥宙 苑涛 戴汉宁† 陈宇翱
1) (中国科学技术大学物理学院,合肥微尺度物质科学国家研究中心,合肥 230026)
2) (中国科学技术大学,中国科学院量子信息与量子科技创新研究院,上海量子科学研究中心,上海 201315)
3) (合肥国家实验室,合肥 230088)
4) (南方科技大学物理系,深圳 518055)
对称性在理解物质的拓扑态方面具有关键作用.过去人们认为手征对称性保证了一维晶格的量子化Zak 相位及其对应的非平庸拓扑相.本文展现了在一维手征对称性破缺的情况下,晶格系统仍具有量子化Zak 相位和非平庸拓扑相.具体而言,在超冷原子动量晶格系统中有效地模拟了一个链长为26、手征对称性破缺的Zigzag 模型,其中相等的次近邻耦合强度能够在保留空间反演对称性的同时破坏手征对称性.通过测量原子的时间平均波包位移来获得系统的拓扑不变量,并得到了其对应的量子化的Zak 相位.此外,还观测到系统随着最近邻耦合强度比例的变化会从非平庸拓扑相转变为平庸拓扑相.本文不仅为对称性及拓扑相的相关研究提供了一个完全可控的平台,还可以通过控制格点间耦合强度和原子间相互作用,探索例如Tasaki,Aharonov-Bohm caging 模型中的平带拓扑以及引入相互作用研究的非线性拓扑现象.
1 引言
二维电子气体中的量子霍尔效应引入了拓扑相的概念[1,2],拓扑相的性质由物质的拓扑性质决定.由于拓扑相在凝聚态物理学[3]中的重要性以及在量子计算[4]、拓扑绝缘体[5]和其他材料科学领域[6]的潜在应用,拓扑相近年来备受关注.而拓扑类可以根据系统的维度和对称性来区分[7],对称性在拓扑相分类方面起关键作用.因此,开展对称性及拓扑相的研究有助于理解拓扑材料的性质.在一维系统中,一般认为非平庸拓扑性受到了手征对称性的保护[7,8].例如,在具有手征对称性的Su-Schrieffer-Heeger (SSH)模型中[9],不同平台的实验结果已经表明SSH 模型确实具有量子化Zak 相位[10]及对应的非平庸拓扑相[11–13].特别地,在超冷原子系统中,人们利用光晶格模拟了SSH 模型并研究了模拟系统的拓扑性质,包括直接测量Zak相位[11],研究模型中受拓扑保护的边界态的鲁棒性[14],以及探索周期驱动的SSH 模型的拓扑性质[15]等.此外,在引入相互作用后还可以研究多体局域化[16]和非线性效应[17]等问题.
在SSH 模型中引入次近邻耦合可以破坏其手征对称性,对应的模型也被称为Zigzag 模型[18–20].在一般的Zigzag 模型中,唯一剩下的对称性就是时间反演对称性.根据Altland-Zirnbauer 分类[21,22],系统处于AI类,无对称性保护的非平庸拓扑相.通过设置次近邻耦合强度相等,系统额外获得了空间反演对称性,此时系统具有对称性保护的非平庸拓扑相[23].目前,人们仅在光子波导系统中对手征对称性被破坏的一维系统的拓扑性质进行了实验研究[24].而超冷原子系统具有精确可控与相互作用可调节的特性,是研究此问题的一个理想平台,同时也有助于开展相互作用引起的拓扑态研究[25,26].
本文在一维超冷原子动量晶格实验中,通过在SSH 模型中引入相等的次近邻耦合,实现了链长为26 的手征对称性破缺Zigzag 系统.利用原子的连续演化过程测量时间平均波包位移以获得系统的拓扑不变量,从而得到相应的Zak 相位信息.同时,通过调节最近邻耦合强度的比例,系统被调制在不同的拓扑物态中,通过时间平均波包位移的测量,观测得到了系统由非平庸拓扑态向平庸拓扑态的转变.本文为对称性及拓扑相的相关研究提供了一个理想的实验平台,可进一步扩展对平带及非线性拓扑的研究.
本文第2 节是Zigzag 模型的对称性、拓扑不变量及拓扑态相关理论;第3 节在实验上对Zigzag模型的拓扑不变量进行测量,并对系统的拓扑态进行分析;第4 节对超冷原子动量晶格中对称性及拓扑态研究进行总结与展望.
2 理论部分
图1(a)为本文要实现的一维Zigzag 晶格模型,该模型由两种格点组成,这里分别被标记为A 和B.由于最近邻耦合和次近邻耦合的存在,粒子会在A 和B 之间、A 和A 之间以及B 和B 之间输运.该系统的哈密顿量为

图1 (a) 一维Zigzag 模型示意图,格点之间的最近邻耦合强度为 u1和u2,次近邻耦合强度为 v1和v2 ;(b) Zigzag 模型的能带分布图;(c),(d)在系统不同的 u1/u2 情况下,Zigzag 模型的环绕数和Zak 相位的变化结果,参数为 v1=v2,v1/u2=0.4Fig.1.(a) Schematic diagram of a one-dimensional (1D) Zigzag model with nearest-neighbor coupling strengths u1 and u2 and next-nearest-neighbor coupling strengths v1 and v2 ;(b) band structure of the Zigzag model;(c),(d) variations of the winding number and Zak phase of the Zigzag model as a function of u1/u2,with parameters v1=v2 and v1/u2=0.4 .
其中,σ0是一个2 × 2 的单位矩阵,σ1,σ2和σ3是泡利矩阵.k为准动量,且-π ≤k≤π .可以求得系统能带的能级色散关系:
图1(b)为v1=v2,v1/u2=0.4且u1/u2=0.5的Zigzag 模型能带图.当v1=v20时,系统两能带的Zak 相位相等,此时Zak 相位γ和环绕数W满足γ=πW.固定v1=v2,当u1
当v1=v20时,系统的手征对称性被破坏,但系统仍然具备时间反演对称性H∗(-k)=H(k)和空间反演对称性σ1H(-k)σ1=H(k) .根据具有空间反演对称性的拓扑分类表[23]可知,AI 类且具有空间反演对称性的系统存在非平庸拓扑相.具体到本系统的拓扑不变量而言,此时系统没有σ3项,系统在布洛赫球表征下被限定σ1-σ2平面绕转,因此系统的拓扑可以由其从一维动量空间到布洛赫球面上的一维空间映射的绕转数确定,其绕转数结果对应于系统的Zak 相位.
为了研究手征对称性破缺系统的拓扑性,可以用一个可观测的物理量来探测此系统的拓扑不变量,这里定义一个物理量平均波包位移:
其中,an(t)和bn(t) 是模型中第n个晶胞中A,B格点的占据振幅.对于一个无限长的演化时间T,时间平均波包位移(time-averaged mean displacement,TAMD)为[24,27]
因此,只要实验上系统经过足够长时间的演化,就可以通过测量TAMD 获得对应的环绕数和Zak 相位.
3 实验部分
图2(a)的上部分为实验上利用Bragg 过程实现一维动量晶格的示意图[28].本文使用数量约为6×104的87Rb 的玻色-爱因斯坦凝聚体(Bose-Einstein condensate,BEC)原子,通过两束波长λ 为1064 nm,波数k=2π/λ,频率分别为ω+和的激光对向传播并耦合出动量晶格的一系列动量态,其中ω+是单频激光,是多频激光.图2(a)的下部分为实验上利用时间飞行测量方法探测单格点的时间相关原子概率分布,通常选择探测原子自由飞行24 ms 后的原子概率分布.
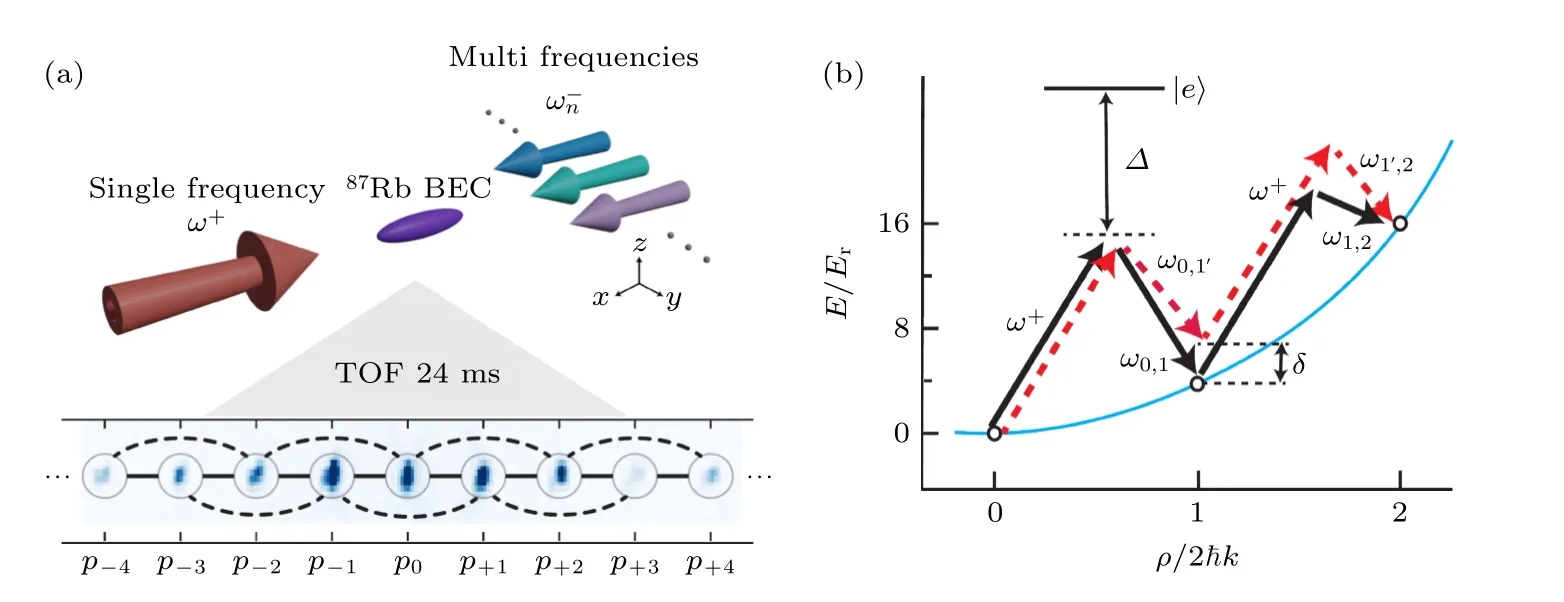
图2 实现一维Zigzag 晶格(a)利用Bragg 过程实现一维动量晶格(上部分)和通过时间飞行成像探测原子数分布(下部分);(b)动量晶格中的原子色散曲线,分别利用一阶和二阶Bragg 跃迁耦合最近邻和次近邻格点Fig.2.Realization of 1D Zigzag lattice: (a) 1D momentum lattice realized using Bragg processes (upper part) and visualized via time-of-flight imaging (lower part);(b) atomic dispersion curve in the momentum lattice includes first-order and second-order Bragg transitions,which are used to couple the nearest-neighbor and next-nearest-neighbor lattice sites.
图2(b)为动量晶格中最近邻和次近邻格点的耦合机制[29],可以通过一阶和二阶双光子Bragg跃迁过程实现格点间最近邻耦合和次近邻耦合的精准调控.利用对打的两束光耦合出一系列动量态作为动量晶格的格点,其对应的动量为pn=2nℏk,反冲能量Er=ℏ2k2/2mRb.对于最近邻动量态p=0 和2ℏk的耦合,需要一阶Bragg 共振(图2(b)中实心黑色箭头w+和w0,1)使两个激光场的光子能量差与具有动量p=2ℏk的运动原子的附加动能相匹配,动量态p=2ℏk和p=4ℏk之间的耦合也类似.所以通过两束具有合适频率差的激光能耦合对应的最近邻动量态pn和pn+1.而为了耦合次近邻动量态,需要同时使用一阶和二阶Bragg 共振(图2(b)中虚线红色箭头).对于次近邻动量态p0和pn=4ℏk的耦合,需要一阶Bragg 共振(图2(b)中虚线红色箭头w+和w0,1′)和二阶Bragg 共振(图2(b)中虚线红色箭头w0,1′和w1′,2)共同实现,所以通过具有合适频率差的激光能耦合对应的次近邻动量态pn和pn+2.这里,∆是单光子失谐量,而δ 是为了避免在次近邻动量态耦合过程中对最近邻动量态耦合产生影响设置的Bragg 双光子跃迁过程失谐量.由于每个最近邻或次近邻耦合相关的动量态对应的频率都是独立的,所以Zigzag 模型的耦合强度、格点能量和耦合相位都可以通过激光的功率、频率和相位进行单独控制.
实验上构建一个链长L=26 的Zigzag 系统,通过引入强度为v1=v2=0.15 kHz 的次近邻耦合,使得系统只有空间反演对称性和时间反演对称性.这里先对一种平庸拓扑态的情况进行观测,此时系统最近邻耦合强度为u1=0.7kHz,u2=0.35 kH,图3(a)为对应的原子在格点间的动力学演化,演化时长为3.1ℏ/u2,时间间隔为0.11ℏ/u2,实验测量结果和数值模拟结果在整个演化过程中都基本符合.根据原子的演化过程可得u1/u2=2时的TAMD,如图3(b)所示,系统的TAMD 在短时间内收敛至0 附近,且和数值模拟的收敛曲线基本符合.根据(5)式可知,对应的环绕数W以及Zak 相位都为0,系统此时处于平庸拓扑相.随后也对一种非平庸拓扑态的情况进行观测,此时系统最近邻耦合强度u1=0.14kHz,u2=0.35 kHz,此条件下的原子在格点间的动力学演化过程如图3(c)所示,整个演化过程中实验和数值模拟结果都一致.同样如图3(d)所示,当u1/u2=0.4 时TAMD 收敛至–0.5 附近,此时W ≈-1 以及Zak相位为-π,系统处于非平庸拓扑相.
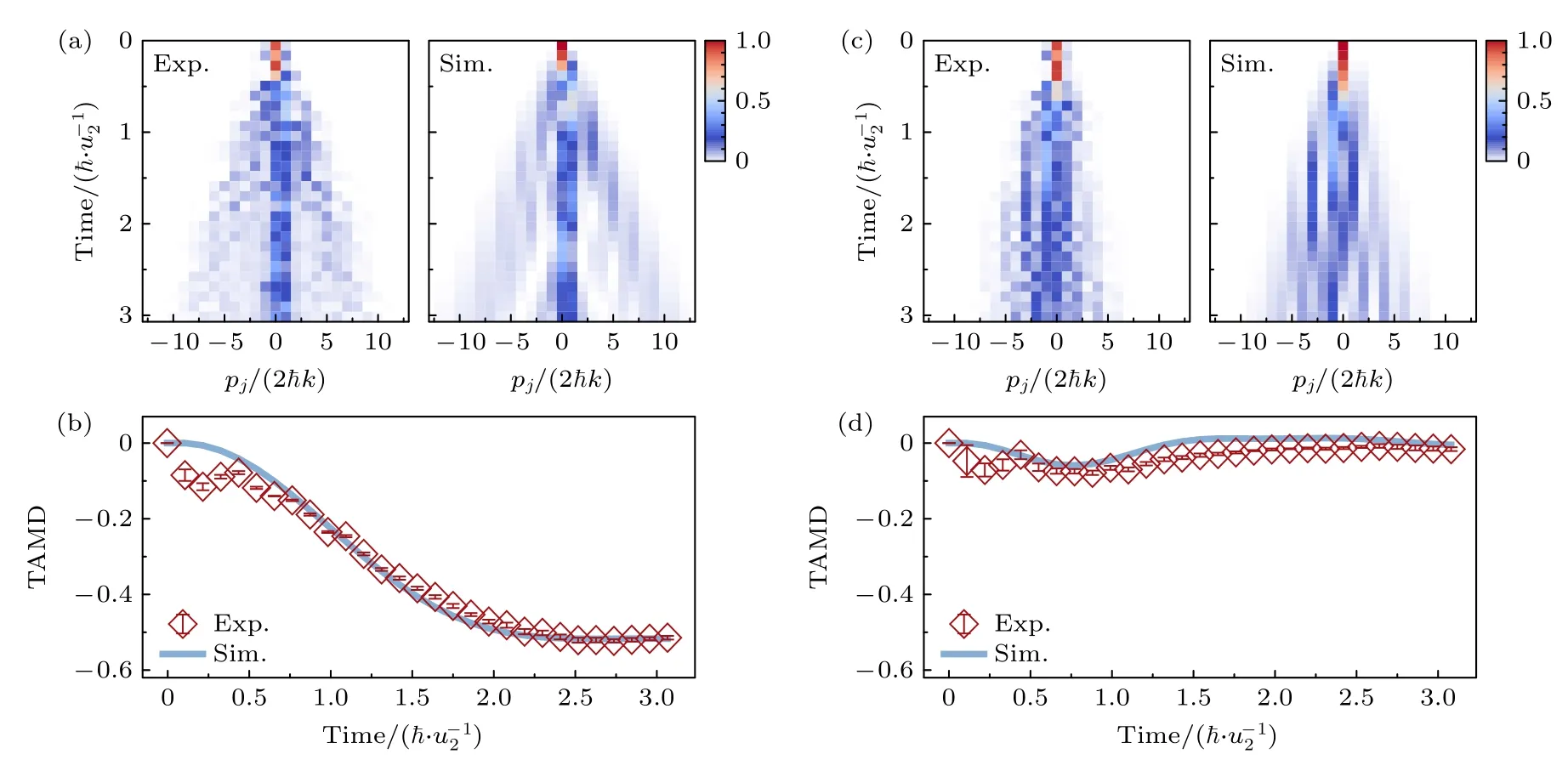
图3 时间平均波包位移的测量(a) u1/u2=2时,系统的动力学演化过程,其中左图为实验结果,右图为数值模拟结果;(b) 通过(5)式得到的图(a)对应的TAMD 的演化结果;(c),(d) u1/u2=0.4时,测量得到的动力学演化过程和TAMD 演化结果.图中采用的实验参数: L=26,v1=v2=0.15kHz,u2=0.35kHz,演化时长为3.1ℏ/u2,时间间隔为0.11ℏ/u2Fig.3.Measurement of time-averaged wavepacket displacement: (a) Dynamics evolution of the system for u1/u2=2,where the left plot shows experimental results,and the right plot presents numerical simulations;(b) evolution of TAMD corresponding to panel (a) obtained using Eq.(5);(c),(d) dynamics evolution and TAMD results were obtained for u1/u2=0.4 .Experimental parameters: L=26,v1=v2=0.15kHz,u2=0.35kHz,an evolution time of 3.1ℏ/u2,and a time interval of 0.11ℏ/u2 .
为观测系统从非平庸拓扑态到平庸拓扑态的转变,对不同u1/u2情况的演化进行了测量,并计算得到了相应的TAMD.理想情况下,当u1/u2<1时,对应的TAMD 收敛值是–0.5,而当u1/u2>1时,对应的TAMD 是0.实验上分别测量了L=26,u2=0.35kHz,v1=v2=0.15 kHz,演化时长为3.1ℏ/u2的Zigzag 模型在u1/u2分别为0.05,0.2,0.4,0.6,0.8,1,1.2,1.4,1.6,1.8,2.0 时的TAMD.结果如图4 所示,系统从u1/u2<1到u1/u2>1 过程中,TAMD 基本从–0.5 逐渐变成0,Zak 相位γ也从–π 转变为0,对应的环绕数W也从–1 逐渐变成0,此时系统从非平庸拓扑相过渡到平庸拓扑相.因此,对于一个手征对称性被破坏的一维晶格系统,其Zak 相位仍然是量子化且存在非平庸拓扑相.
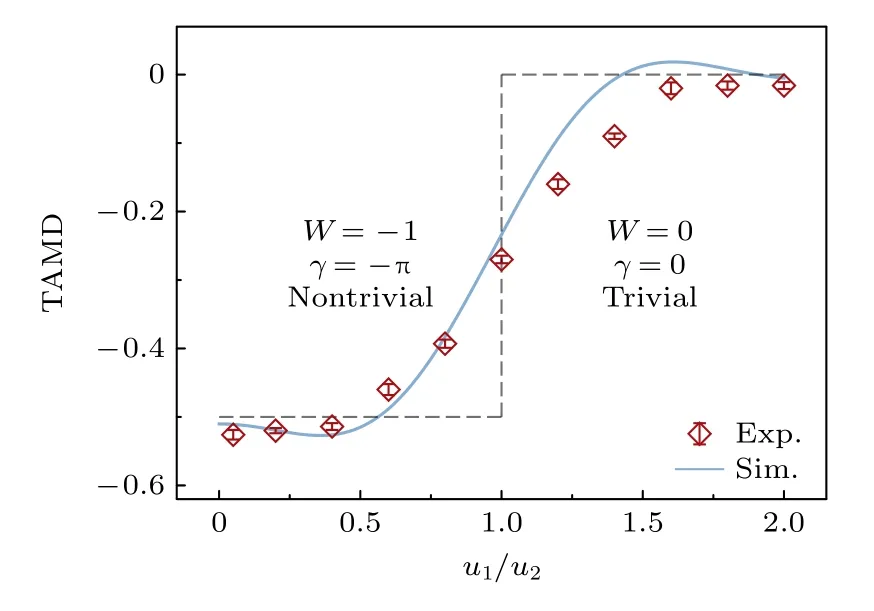
图4 不同 u1/u2 的Zigzag 模型对应的TAMD 变化曲线.图中灰色虚线是理想模型对应的结果Fig.4.Variation curves of TAMD for different u1/u2 in the Zigzag model.Gray dashed lines indicate results from the ideal model.
4 结论
本文研究了动量晶格系统中一维手征对称性破缺晶格系统的拓扑性.实验上利用87Rb 原子的BEC 模拟链长为26 的一维Zigzag 系统.通过调制激光功率使得所有次近邻格点耦合强度都相等,此时系统手征对称性被破坏.基于原子的连续演化过程测量时间平均波包位移以获得系统的拓扑不变量,证明了一维手征对称性破缺晶格系统仍具有量子化Zak 相位和非平庸拓扑相.此外,还观测到在u1/u2=1时,系统从非平庸拓扑态转变成平庸拓扑态.本工作为对称性和拓扑相的相关研究提供了一个完全可控的平台,可进一步引入相互作用研究非线性拓扑现象[17].此外,还可以用于研究基于SSH 模型的拓展模型.例如研究加上长程的格点耦合的拓展SSH 模型的相变临界现象[30]和平带能级结构[31],以及不同对称性对拓展SSH 模型拓扑性质的影响[20].通过控制格点间耦合强度,探索具有更多能级结构的模型的拓扑性质,比如三能级结构的Aharonov-Bohm caging 模型[32–35]具有的奇异平带性质.
