基于归一化求导的裂纹缺陷涡流检测信号处理方法
2024-03-18李朋宇荆林远王高洁闻东东
李朋宇,闫 帅,荆林远,王高洁,闻东东
(1.国网安徽省电力有限公司 亳州供电公司,亳州 236800;2.徐州工程学院 电气与控制工程学院,徐州 221000)
压力容器的管道、锅炉、容器等关键金属零部件在制造和服役过程中均需实施无损检测[1]。常规涡流检测具有响应速度快、无接触、效率高、成本低等优点,已广泛应用于金属构件的疲劳裂纹、腐蚀损伤检测[2-3]。在压力容器疲劳裂纹缺陷的涡流检测中,提离变化、包覆层、不规则曲面、应力变化等影响因素会导致检测精度降低,甚至引发误检、错检等问题,严重威胁压力容器的质量安全[4]。其中,材料应力变化作为容易忽略的影响因素,不仅会对检测信号产生较大干扰,甚至会导致出现错误的检测结果。因此,抑制应力变化对裂纹缺陷涡流检测的影响是当前亟待解决的关键问题。
为抑制涡流检测变化因素对缺陷检测结果的影响,众多学者开展了相关研究。吴斌等[5]研究了线圈弯曲角度变化对柔性涡流传感器缺陷检测能力影响,结果表明,圆形线圈的弯曲会导致各向均匀涡流场朝单向涡流场转变,无论是工作在自感还是互感检测模式下,柔性涡流传感器对不同方向裂纹的检测灵敏度均降低。杜金强等[6]研究了互扰对阵列涡流传感器裂纹检测的影响,结果表明,互扰会导致阵列传感器输出信号幅值显著减小、相位出现偏移,也会对阵列涡流传感器的裂纹检测灵敏度产生一定影响;若以跨阻抗幅值作为传感器的特征量,互扰对裂纹检测灵敏度的影响可以忽略。杨帆等[7]提出了一种U形磁导体聚焦探头,通过探头中的U形磁导体结构引导磁场使涡流聚集于磁导体探头下方,避免了圆柱探头的涡流检测盲区实现了对不锈钢板局部缺陷的检测,且不受大提离的影响。杨理践等[8]提出了一种基于平衡电磁技术的检测方法,该方法在交流励磁条件下利用U形传感器能实现该方法对钢板表面横纵向裂纹进的效检测,通过信号特征能够有效区分裂纹类型。综上所述,现有研究对裂纹缺陷检测影响因素的抑制,主要集中在探头提离、探头结构、信号处理方法等方面,鲜有研究关注材料应力变化对裂纹缺陷检测结果的影响。
铁磁性材料的应力变化会改变其材料的电磁特性,即会改变铁磁性材料的电导率和磁导率等参数,进而影响涡流检测的结果[9]。因此,抑制或消除铁磁性材料应力变化对涡流检测结果的影响是当前亟待解决的关键问题。针对此问题,笔者提出了一种涡流检测信号的应力变化影响抑制方法,有效提高了铁磁性材料裂纹缺陷的涡流检测精度,也为其他铁磁性材料损伤检测的应力变化影响抑制提供了一些借鉴。
1 理论分析
根据磁致伸缩理论和磁弹性理论[10-11],当铁磁性材料被磁化和受到外部应力时,铁磁性材料磁导率的变化可以表示为
ε=EHσ+dH
(1)
B=d-1σ+μH
(2)
式中:ε为应变;EH为特定磁场条件下的杨氏模量;σ为应力;d为压磁系数;H为磁场强度,B为磁感应强度;d-1为反压磁系数;μ为磁导率。
式(1),(2)表示的是铁磁性材料在弹性应变范围内的磁场变化关系,即弹性应力作用在铁磁性材料时,其磁场分布将发生变化。因此,磁弹性效应会影响铁磁性材料裂纹缺陷的检测。根据焦耳效应[12],铁磁性材料应变ε和磁导率μ的关系可以表示为
(3)
式中:λs为磁致伸缩常数;Ms为饱和磁化强度;Kμ为单轴磁各向异性常数;Δμ为磁导率的变化量;θ0为磁场与磁化轴之间的夹角。
根据胡克定律[9]可知,铁磁性材料应变ε和作用应力F之间的关系可以表示为
F=εEA=σA
(4)
式中:E为弹性模量;A为铁磁性材料的横截面积。
将式(4)代入式(3)中,可以获得
(5)
当被测铁磁性材料确定时,式(5)中E、λs、Ms、Kμ和θ0是确定的常数。当环境磁场强度H不变时,磁导率变化量Δμ是随着应力σ变化而变化的。
涡流检测模型如图1所示,假定板材是线性、各项同性、均匀的介质,由电磁感应原理和麦克斯韦方程可求出谐波激励下的磁通密度大小[13],即
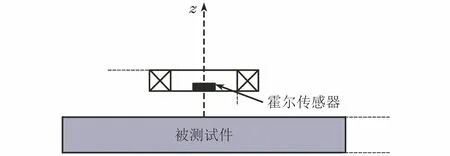
图1 涡流检测模型
B=Bs+Bec
(6)
式中:Bs为探头在空气中的磁通密度;Bec为探头在被测试件上方时涡流感应的磁通密度。
Bec是与电导率和磁导率相关的系数,磁敏传感器检测到的涡流场感应磁通密度与被测试件的电导率、磁导率和厚度参数相关。由式(5)可知,磁导率变化量随着应力的变化而改变。综上所述,被测试件应力的变化会影响探头的感应磁通密度,即被测试件应力的变化会影响涡流检测信号。
2 归一化求导方法
针对应力变化对铁磁性材料裂纹缺陷涡流检测的影响,笔者提出了一种抑制方法,其流程如图2所示,主要包括信号特征获取、归一化和求导处理等步骤[14-16],旨在通过信号处理的方法抑制应力变化对裂纹缺陷检测的影响。其中,信号特征是检测信号数据的标准差值;线性扫描检测主要是对被测试件进行线性单向扫描检测;归一化处理主要是对线性扫描检测获取的信号特征进行处理;求导处理主要是对归一化信号的特征数据进行求导变换。

图2 归一化求导方法流程
V=[Vt1,Vt2,…,VT]
(7)
式中:t1为信号采样时间;T为信号采样周期。
(2) 对获取的检测信号进行特征提取,即对周期检测信号数据求均方差,得到检测信号的均方差特征信号,即
(8)

(3) 利用上述单点检测信号特征进行线性A扫检测,即对试件进行线性多点扫描检测,以获取检测信号均方差信号特征数据,即
σ=[σV1,σV2,…,σVN]
(9)
式中:N为扫查点数。
(4) 对上述检测信号的均方差特征数据进行求导处理[17],以提高特种信号的信噪比,可写为
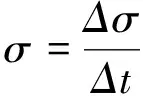
(10)
式中:∇σ为导数信号数据;Δσ为单位时间内均方差信号变化量;Δt为信号采样时间间隔。
(5) 对上述线性扫描获取的均方差导数信号进行归一化处理[18],以抑制外部干扰对导数信号的影响,可写为
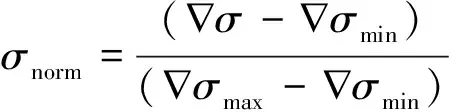
(11)
式中:∇σmax为导数信号数据的最大值;∇σmin为导数信号数据的最小值。
(6) 对处理后的信号数据进行成像,实现对裂纹缺陷的精确定量评估。
3 检测系统与试验材料
应力状态下试件涡流检测试验现场如图3所示,检测系统主要包括数据采集系统、三维移动扫描平台、拉伸机等。其中,数据采集系统包括计算机、PCI-1814型数据采集卡、GWINSTEK-AFG-2225型函数发生器、GWINSTEK-GDS-2102E型示波器、功率放大器、探头等模块。探头结构如图4所示,其外圆半径为10 mm,内圆半径为5 mm,高为18.5 mm,激励线圈匝数为300匝,线径为0.1 mm。检测时通过数据采集卡将信号数据传输至计算机保存,同时,检测信号也在示波器上实时显示出来,便于监测。三维移动扫描平台包括计算机、步进电机控制器、三维扫描机构等。计算机通过步进电机控制器完成对步进电机行进距离的控制,以实现对移动平台的行进点位控制。拉伸机装置包括液压缸、应力传感器、计算机、应力监测仪、专用夹具等。试件固定于夹具上,通过液压缸机构实现对试件的拉伸,同时,应力传感器实时检测应力大小,并通过应力监测仪实时传送至计算机。试验所用试件材料为Q235钢,其结构如图5所示。

图3 应力状态下试件涡流检测试验现场
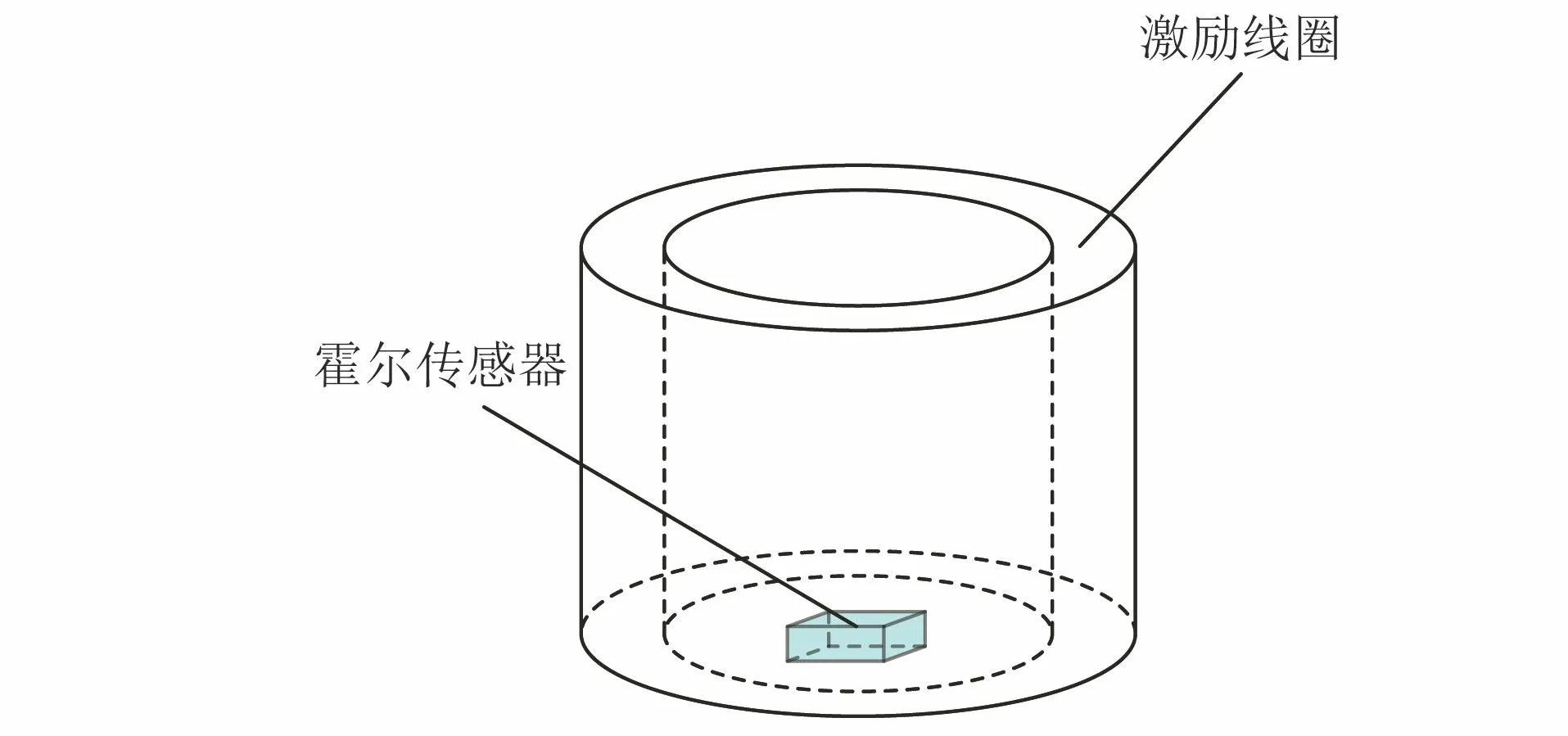
图4 探头结构示意
4 试验过程与试验结果
试验中,采用函数发生器生成正弦激励信号,其幅值为2 V,频率为200 Hz。正弦激励信号经过功率放大器放大后施加至探头激励线圈。数据采集卡采样频率为1 MHz。A扫方向如图5所示,步进距离为0.25 mm,扫查一个点的时间间隔为1 s,扫查距离为157 mm。在不施加拉伸应力的条件下,试件无裂纹缺陷处检测获取的信号如图6所示,可见,信号曲线不是关于时间轴的对称曲线,而是存在一定偏移量,即检测信号是无过零点的变化曲线。在信号特征提取中,经分析发现,相比于检测信号数据的均方差信号特征,峰值信号更易受应力变化影响,且A扫裂纹缺陷的信号变化量也小于均方差信号特征的变化量。即,在受应力变化影响的裂纹缺陷检测中,均方差信号特征稳定性优于峰值信号特征。
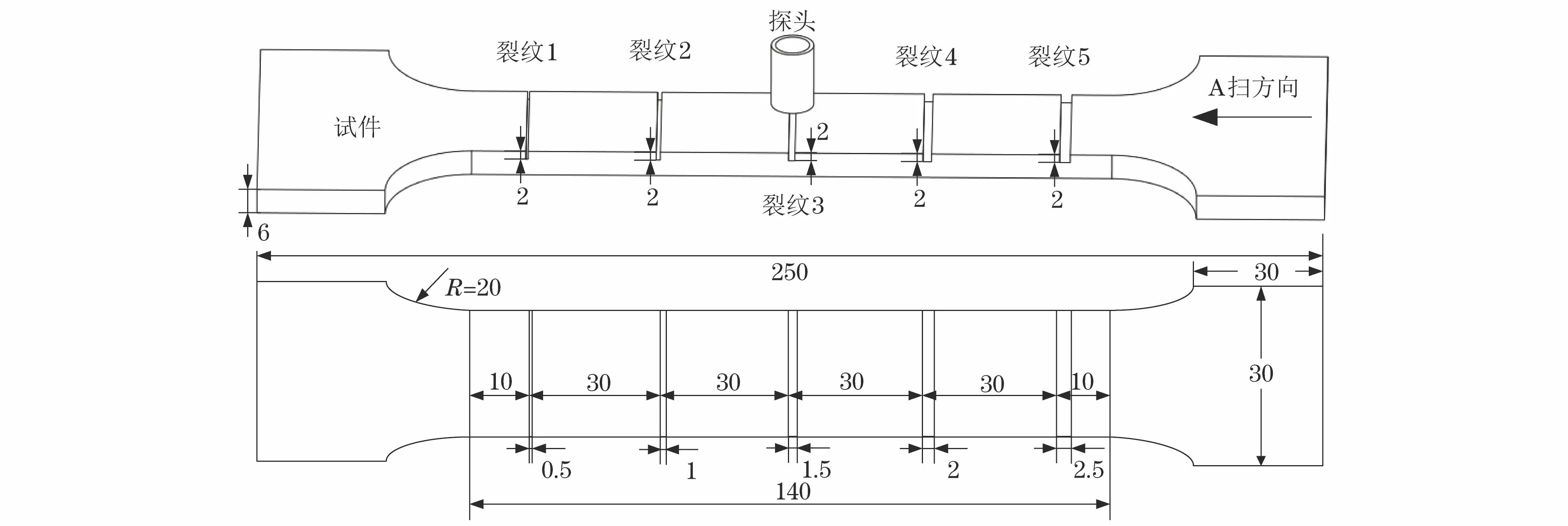
图5 试件结构示意
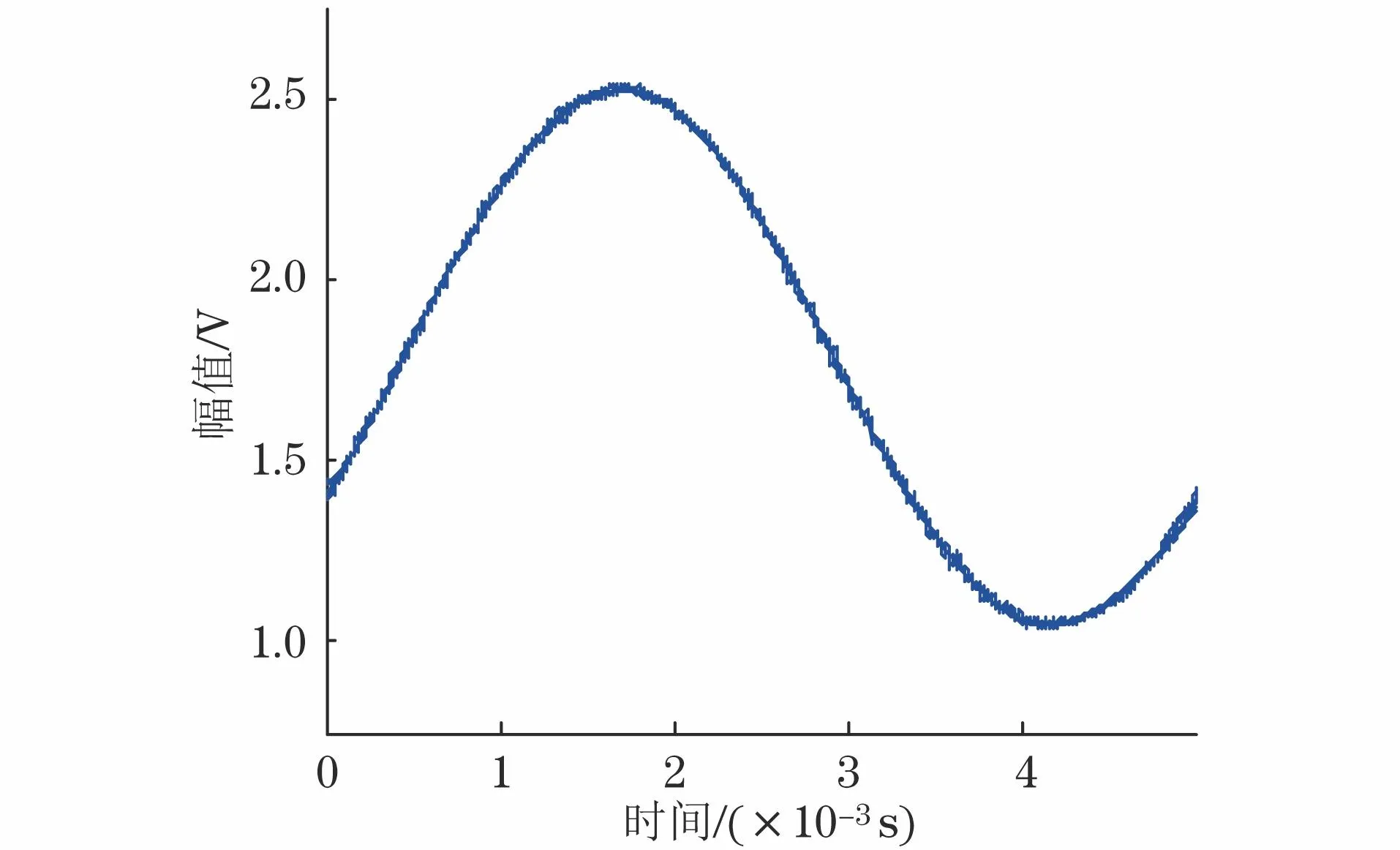
图6 试件无裂纹缺陷处的检测信号曲线
接着,用所提方法对去噪后的涡流检测信号进行处理,计算出周期检测信号的均方差值,并作为信号特征数据,对裂纹进行A扫检测,获取的A扫均方差信号曲线如图7所示。由图7可知,随着探头移动距离的增加,均方差信号在裂纹处呈现明显变化,即随着裂纹宽度的增加峰值变化量逐渐增大;然而,宽度为0.5 mm的裂纹处的峰值信号没发生明显变化。这是由于试验扫描平台的精度有一定限制,说明更小步进距离的扫描平台可以提升扫查信号的显现效果。因此,只有A扫步进距离小于裂纹宽度的1/2时,才能有效裂纹缺陷。另一方面,从图7中也可以观察到,随着扫查距离的增加,均方差信号总体呈现增加的变化趋势,仅在裂纹处有减小。

图7 裂纹的A扫均方差信号曲线
当对试件作用不同的拉伸应力时,其A扫均方差信号随应力的变化曲线如图8所示,可见,随着拉伸应力的增加,均方差A扫信号出现明显变化。在初始段A扫位置,裂纹处的均方差信号变化量呈现减小的变化趋势。在A扫末段位置,均方差信号的变化量呈现增加的变化趋势,且裂纹处的均方差信号幅值也有所差异。由此可知,裂纹缺陷的均方差信号会受到应力变化的影响,且在A扫信号的起始段和末段变化不同。该应力变化结果会对裂纹缺陷的定量评估造成较大影响,引起裂纹缺陷A扫均方差信号的误判或错判。因此,抑制金属材料应力变化对裂纹缺陷检测的影响是尤为重要的工作。
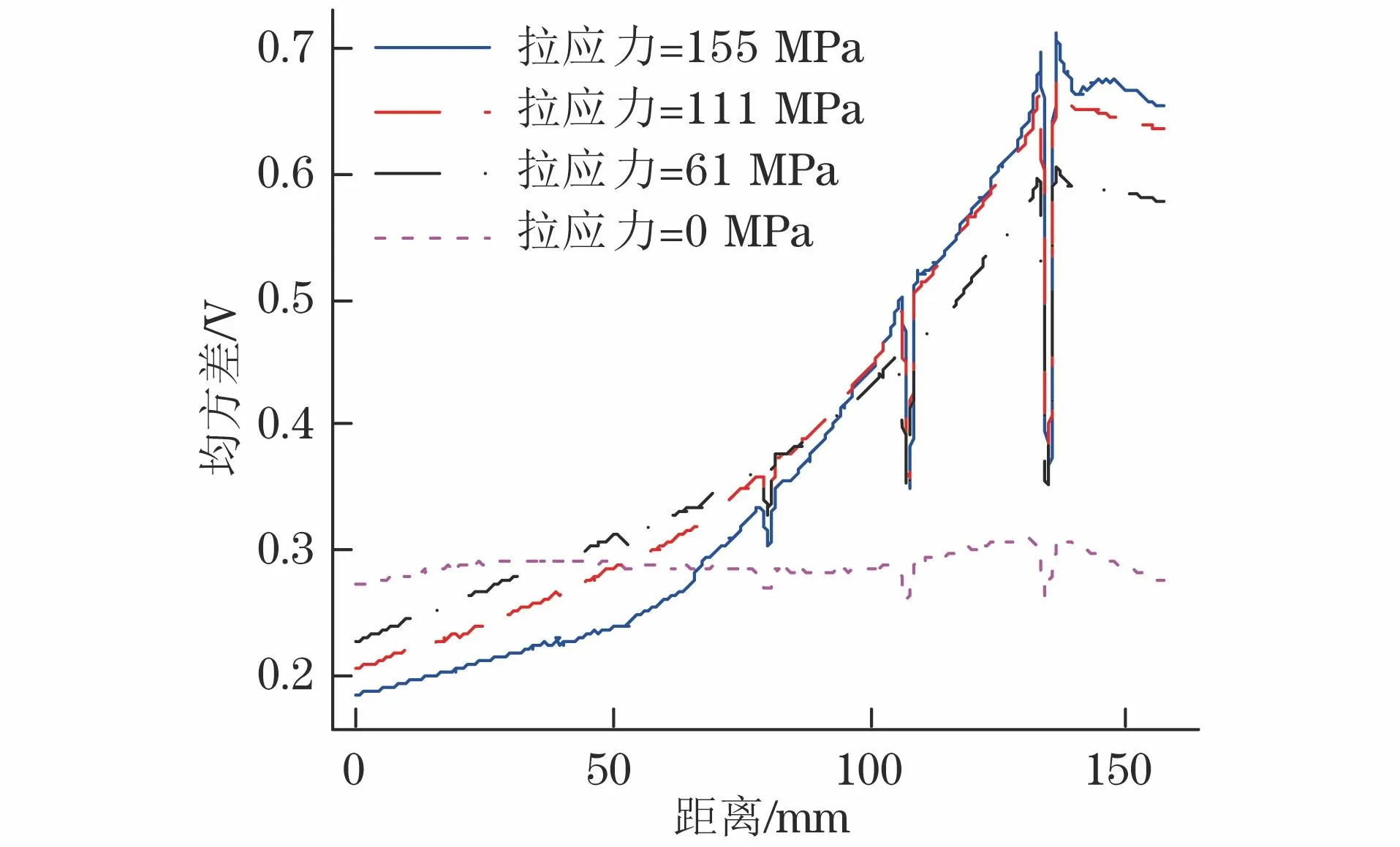
图8 A扫均方差信号随应力的变化曲线
对上述均方差信号进行求导处理,获取的求导后均方差信号变化曲线如图9所示。由图9可知,求导后的均方差信号呈现出以横轴为中心的对称状态,且随着裂纹宽度的增加均方差信号幅值增加,同时求导后的均方差信号受应力变化的影响得到了一定程度的抑制。
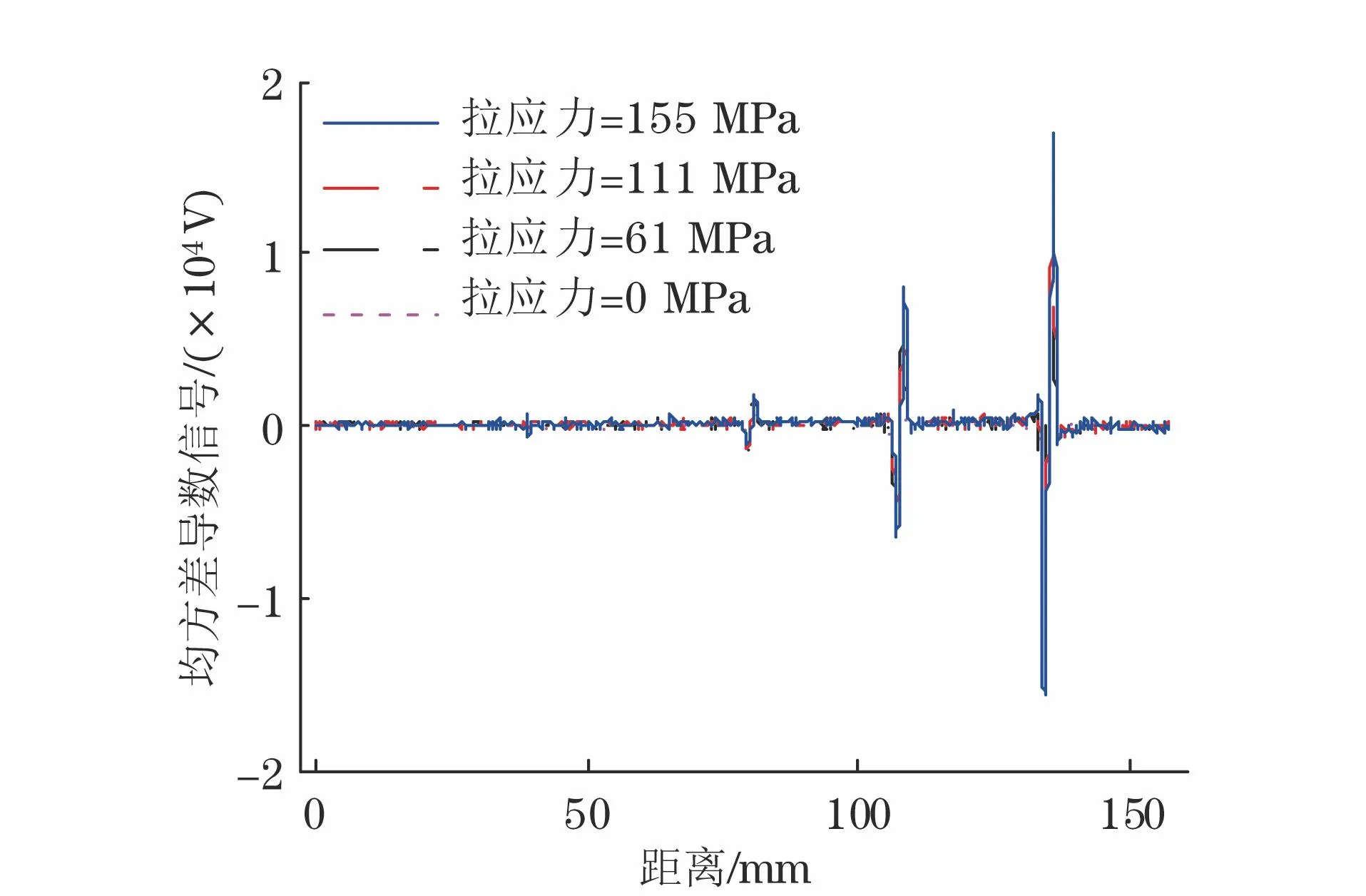
图9 不同应力时的求导后均方差信号变化曲线
进一步,对随应力变化的导数信号进行归一化处理,其结果如图10所示。由图10可知,不考虑零拉伸应力的条件下,经归一化处理后应力对导数信号的影响得到抑制,在A扫末段和初始段,裂纹导数信号变化得到较好抑制。但是,归一化导数信号在应力变化的条件下,仍会发生一定变化,且在A扫中段的变化相对明显。对比不同宽度的裂纹缺陷信号发现,峰峰值位置A扫信号特征变化量的横向距离几乎一致,即说明峰峰值位置A扫信号变化量的横向距离不能用于评估裂纹宽度大小。但随着裂纹宽度的增加,裂纹处的归一化导数信号幅值增加,即归一化导数信号幅值的变化量参数能够用于评价受应力变化影响的裂纹缺陷宽度大小。

图10 不同应力时的归一化导数信号
基于上述试验结果,笔者利用归一化导数信号幅值的变化量参数来评价裂纹缺陷宽度大小,建立归一化导数信号幅值变化量与裂纹宽度大小的映射关系,形成的归一化导数信号幅值变化量随裂纹宽度变化曲线如图11所示。由图11可知,随着裂纹宽度的增加,归一化导数信号的幅值变化量增加。即,通过归一化导数信号的幅值变化量可以评价受拉伸应力变化影响的裂纹宽度大小。对比均方差信号幅值变化量与裂纹宽度的关系,其结果如图12所示,发现随着裂纹宽度的增加,均方差信号在裂纹处的幅值变化量增加,受应力变化影响更加明显。

图11 归一化导数信号幅值变化量随裂纹宽度变化曲线
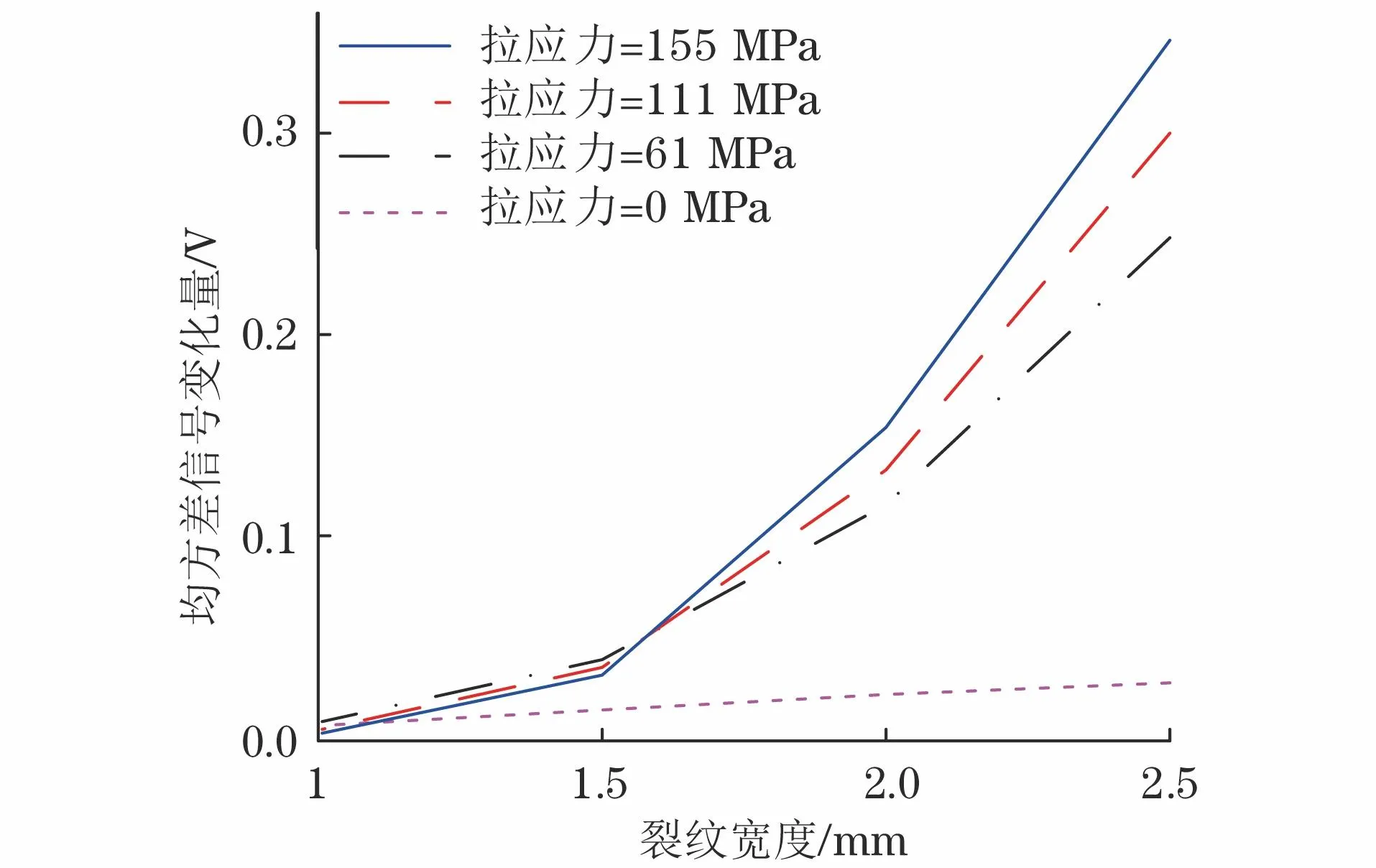
图12 均方差信号变化量随裂纹宽度变化曲线
由上述分析可知,利用提出的应力变化影响抑制方法对检测信号进行处理后,有效抑制了应力变化对裂纹缺陷检测的影响,提高了裂纹缺陷的涡流检测精度。
5 结果讨论
综合上述分析,所提出的应力影响抑制方法可以有效减小应力变化对裂纹缺陷宽度检测的影响。在实际应用中,金属材料都会承受到不同大小或方向的应力作用,同时,金属材料自身也存在残余应力。在实际工程应用中,金属材料都处于弹性应变区间,试验中被测试件所受拉伸应力也仅考虑了金属材料弹性形变范围内的应力影响,未考虑塑性形变范围内的应力变化影响。
对裂纹缺陷涡流检测的应力影响抑制方法作进一步分析,计算出在应力变化影响条件下均方差信号和归一化导数信号的裂纹缺陷检测精度,结果如图13所示,可见裂纹缺陷宽度为1~2.5 mm时,均方差信号的最大相对误差达到50%,而归一化导数信号裂纹缺陷检测的相对误差小于10%。相比而言,提出的方法可以有效降低在应力影响下的检测误差,对于宽度较小或较大的裂纹缺陷,该方法检测精度更高。
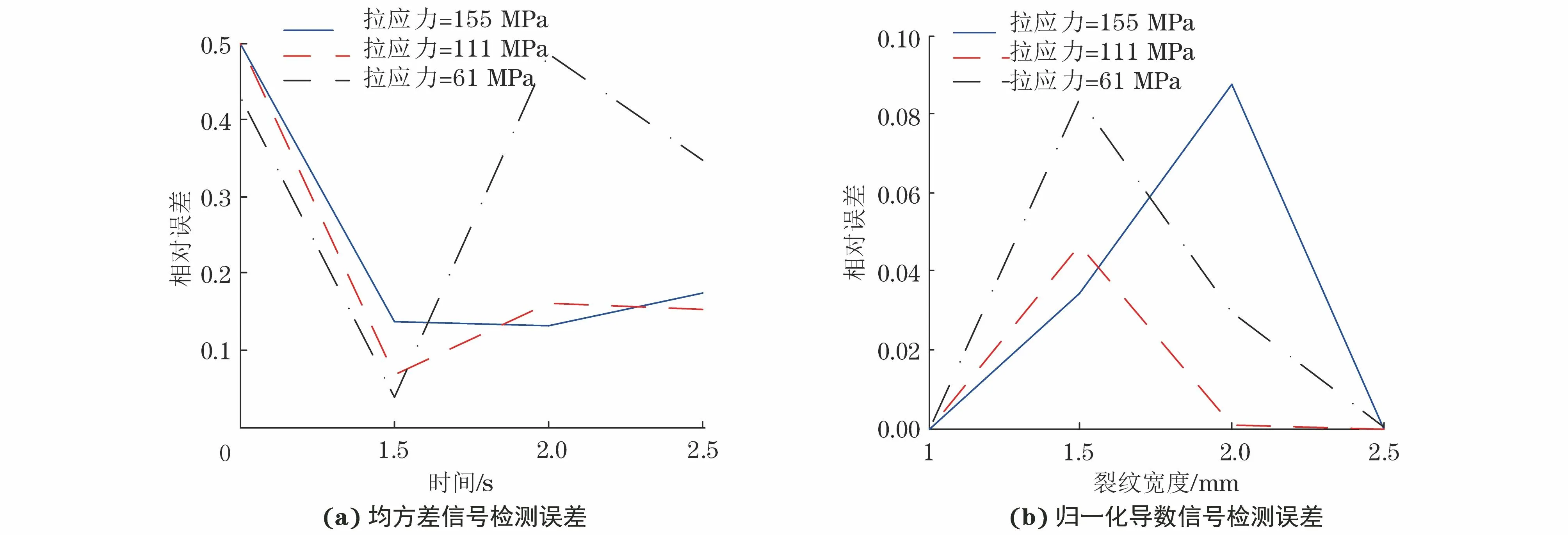
图13 均方差和归一化信号的裂纹缺陷检测误差
6 结语
针对应力变化对裂纹缺陷涡流检测结果的影响,提出了一种应力影响抑制方法。该方法通过均方差求解获取A扫检测的信号特征,并进一步利用求导方法对A扫检测信号进行处理,得到均方差导数信号,然后,利用归一化方法对导数信号进行处理,获得归一化导数信号,最终,通过归一化导数信号的幅值变化量对裂纹缺陷进行评价,实现应力变化条件下裂纹缺陷的精确定量。试验结果表明,提出的方法可有效抑制应力变化对裂纹缺陷检测的影响,提高裂纹缺陷检测精度。
