管内充分发展流动与传热数值模拟的教学方法探讨1)

毛宇飞 上官燕琴 肖 洪

(河海大学机电工程学院，江苏常州 213022)

笔者多年来从事能源与动力工程专业的本科教学工作，在指导学生进行本科毕业设计过程中，发现学生学习了流体力学、工程热力学和传热学等专业基础知识，也学习了计算机编程语言，但在将程序设计应用于工程计算这方面却掌握得非常薄弱。因此，笔者结合教学实践和研究方向，给本科学生开设了一门专业提升课程——热工计算与程序设计。与本科引入计算流体力学（computational fluid dynamics，CFD）软件教学[1]不同，该课程要求学生针对流体力学、热力学和传热学领域的一些典型算例，进行数学建模、程序设计及计算分析。通过该课程的学习，训练学生编写MATLAB 程序，将流体物性计算、物理过程数值计算、数据处理及图像绘制设计成一个整体[2-3]，课程的教学思路与同济大学付小莉老师的工作[4]有相似之处。

管内不可压缩流体充分发展流动与传热是一个很常见的工程问题，层流工况时存在理论解析解，湍流工况时存在近似解和经典公式，是计算流体力学和数值传热学课程中一个很好的入门算例。目前，学生围绕该算例进行程序设计和数值模拟，通常是在研究生阶段完成的[5]，这是因为相关计算数学理论超出了本科生的知识储备。本文将边界层积分方法应用于管内充分发展流动与传热的数值模拟，从而简化了数值求解过程；并基于数值积分和有限差分法（或有限容积法），发展出适用于层流和湍流工况下管内对流传热的数值计算方法。论文对该数值方法的数学原理和程序设计方案进行了详细阐述，对该工程算例的教学过程进行了较完整的教学设计。

1 边界层积分控制方程组

1.1 物理过程

当流体进入管道与管壁表面接触时，在黏性摩擦的作用下，近壁处的流体速度变慢，形成边界层。沿流动方向边界层逐渐增厚，而管中心的无黏流动区则逐渐缩小，直至边界层充满整个管道，形成流动充分发展段。层流充分发展区速度场遵循Poiseuille 抛物线分布规律，湍流充分发展区速度场则遵循幂律（power-law）分布规律[6-8]。将边界层概念从速度边界层推广至温度边界层，这奠定了对流传热分析的理论基础。

边界层积分求解方法已被成功应用于不可压缩流体外掠平板（直角坐标系）层流对流传热，引入合理假设后可采用数学方法直接求出摩擦阻力系数和对流传热系数的近似解[6-8]。本文将边界层积分法引入管内充分发展流动与传热（圆柱坐标系），展开理论分析与数值计算。建立边界层积分方程组有两种方法，一种是对边界层微分方程沿边界层厚度积分得到，另一种是对坐标系内控制体进行质量、动量和能量守恒分析而导出。两种方法殊途同归，具体推导过程可参阅相关文献中关于外掠平板的边界层积分方程组[6-8]。

1.2 动量方程

在管内流动充分发展区，对于不可压缩流体，沿流动方向（x坐标方向）的速度u分布不再变化，即∂u/∂x=0，同时径向（r坐标方向）速度v可以忽略，这意味着稳态轴对称条件下连续性方程自动满足。此外，沿流动方向的压力梯度可视为常数。因此，流动方向的动量方程可简化为

式中，τ 为剪切应力，τw为壁面剪切应力；层流流动时μeff=μ，μ为流体动力黏性系数；湍流流动时μeff=μ+μt，μt为湍流（动力）黏性系数；R为管道半径；y为离开管壁面的距离,y=R-r。

定义无量纲距离Y，无量纲半径η 和无量纲速度U为

式中，d为管道直径，d=2R。将式(2)代入式(1)化简得到

式(3)即为采用积分方法得到的动量（无量纲速度）方程，这是一个一阶偏微分方程，其边界条件为：Y=0，U=0；Y=1，方程自动满足轴对称条件。

工程计算中，可以选择简单实用的混合长度理论来计算圆管内充分发展区的湍流黏性系数[5-8]

式中，ρ 为流体密度，l表示混合长度。将式(4)无量纲化

式中，Re为Reynolds 数，v为流体运动黏性系数（v=μ/ρ），ub和Ub分别为整个管道流动截面上流体的平均速度和平均无量纲速度。不可压缩流体的Ub计算公式为

黏性底层外的混合长度l可根据Nikurades公式计算[5]；而在近壁处的黏性底层中，需引入Van Driest 阻尼函数DF来修正分子黏性对湍流脉动的影响[5]。因此，一个适用于圆管充分发展湍流边界层的混合长度计算式为

式中，y+为无因次距离。

根据壁面剪切应力τw与Darcy 摩擦阻力系数f之间的关系，导出f的计算式

1.3 能量方程

基于稳定流动开口系统能量方程，对管内充分发展对流传热温度边界层进行积分并无量纲化得到

式中，q为（半径r截面）热流密度，qw为壁面热流密度，T为流体的温度。工程中管内对流传热通常存在两种典型工况：均匀热流边界和均匀壁温边界。下面就这两种不同工况对式(9)进行化简。

1.3.1 均匀热流工况

若流体热物性随温度的变化忽略不计，进入热充分发展段后，对流传热系数将保持常量。因此，在均匀热流条件下，根据流体温度变化关系[6-8]可将式(9)转化为

式中，Um为半径r流动截面上流体的平均无量纲速度，计算公式为

定义无量纲温度Θ

式中，Tw为壁面温度，λ 为流体导热系数。根据热流密度的定义，将式(12)代入式(10)化简得到均匀热流条件下的能量（无量纲温度）方程

式中，Pr为流体的Prandtl 数；Prt为湍流Prandtl 数。式(13)的边界条件：Y=0，Θ=0；Y=1，方程自动满足轴对称条件。工程计算中，Prt通常取0.9～1.0 之间的定值[5]。考虑到不同流体Pr数的变化，本文推荐采用下面经验方法[9]计算Prt

由式(14)，Pr=1 时，Prt=1；Prt随Pr的增大而减小。应用式(14)，可将本文的数值方法推广至低Pr数工况。

1.3.2 均匀壁温工况

在均匀壁面温度条件下，根据热充分发展区的温度变化关系[6-8]，对式(9)进行化简并无量纲化，得到均匀壁温工况的能量（无量纲温度）方程

式(15)的边界条件与式(13)完全一致。式中，Θm为半径r流动截面上流体的平均无量纲温度，Θb为整个流动截面上流体的平均无量纲温度，定义为

Θb与表征对流传热系数h的Nusselt 数Nu之间存在确定的数学关系

综上所述，通过边界层积分方法，将表征管内充分发展流动与传热的二阶偏微分方程组简化成边界条件完全一致的一阶偏微分方程组，从而可以使数值计算过程得到明显简化。

2 数值计算方法

2.1 网格生成及控制方程离散

根据前面推导的边界层积分控制方程组可知，管壁处无量纲变量U或Θ均等于零，故数值计算可从管壁向管心推进。采用内节点法对无量纲坐标Y方向计算区域进行离散，将第1 个节点布置在管壁处（Y=0），最后一个节点（M1节点）布置在管心（Y=1）。考虑到近壁处区域内速度场和温度场变化剧烈，此处网格应布置稠密一些（越靠近管壁，网格越密）。通常可以采用定比加密或指数加密两种方法生成网格[5]，两种方法均可得到满意的数值模拟结果。

采用边界层积分法得到的动量方程和能量方程均为一阶偏微分方程，且壁面处（节点1）U和Θ均等于0，因此可以采用数值积分方法对控制方程进行离散，得到求解节点2～M1处U和Θ的代数方程组。控制方程组对应的离散方程可以采用如下统一形式

式中，I为节点编号，I=1～M1；YCV表示控制容积（I=2～M1-1）的宽度，YCV(2)=YCV(M1)=0；针对不同的流动与传热工况，Φ，A，B和C对应的表达式或数值见表1。

表1 式(18)中的Φ，A，B 和C

2.2 速度场和温度场的求解

对于不可压缩（常物性）流体，流动过程和传热过程相互独立，因此可以单独求解动量方程获得速度场分布，再将速度场分布代入能量方程求出温度场分布。

层流流动时，根据式(18)可依次求解出节点2 至节点M1的无量纲速度，无需迭代。湍流流动时，由于湍流黏性系数取决于速度场分布，因此应用式(18)数值求解各节点U时需要迭代计算；计算过程中，湍流黏性系数式(5)中的无量纲速度梯度∂U/∂Y采用二阶精度的差分表达式；迭代收敛的判据是节点相邻两次计算值的最大相对偏差的绝对值小于10-6。求得各节点处的无量纲速度U，并获得网格独立解后，根据式(6)通过数值积分求得Ub，再根据式(8)求得摩擦阻力系数f。

求出无量纲速度场后，根据式(11)采用数值积分求出各节点对应半径流动截面上流体的平均无量纲速度值Um，进而代入能量方程进行计算。对于均匀热流条件，根据能量方程式(13)，将Um，Ub和μt/μ（湍流工况）代入式(18)直接求解出各点的无量纲温度，无需迭代。对于均匀壁温条件，求解能量方程式(15)时，不仅需要确定速度场，还需要获得温度场信息；因此计算时，先设定Θ迭代初场，根据式(16)通过数值积分求得Θb和Θm，再应用式(18)计算求解出各节点的Θ，反复迭代，直至收敛，收敛条件与求解U方程一致。获得网格独立解后，再根据式(17)求得表征对流传热能力的Nu数。

根据上述分析，均匀壁温条件下管内湍流流动与传热的数值模拟最为复杂，对应速度场和温度场均需迭代求解，其具体的数值求解过程如图1 所示。针对不同的流动与传热工况，采用MATLAB 编写计算程序和绘图程序，对相关计算结果进行比较分析。

图1 均匀壁温管内湍流流动与传热数值求解过程

3 计算结果与分析

3.1 层流流动与传热

计算表明，基于边界层积分方程的算法具有较快的收敛速度。图2 给出了层流工况下网格数对摩擦阻力系数f和传热Nu数的影响。在计算速度场时，即使网格（控制容积）数为1，此时内部节点的计算值与精确值相差较大，但由于整个边界层满足总体的动量守恒，Ub的计算值等于精确值，因此阻力系数预测值始终与解析解（f·Re=64）吻合。随着网格数的增大，速度场不断趋近精确值，温度场也逐渐收敛；当网格数大于30，层流对流传热Nu数已基本与精确值（均匀热流Nu=4.364，均匀壁温Nu=3.658）吻合。根据获得的网格独立解情况，层流工况的网格数取50，湍流工况（Re＜106）的网格数取200。

图2 层流工况下网格数对计算结果的影响

图3 和图4 分别给出了管内层流充分发展条件下无量纲速度场和无量纲温度场的模拟结果。速度场与解析解、均匀热流工况温度场与解析解非常吻合。均匀壁温条件下的温度分布比起均匀热流条件下的更不均匀，因此均匀壁温工况的管道截面上Θb值较大，相应Nu数较小。

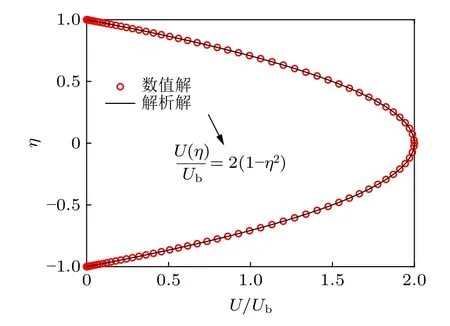
图3 管内层流充分发展速度场模拟结果

图4 管内层流充分发展温度场模拟结果

3.2 湍流流动与传热

已有研究[6-8]表明，管内湍流充分发展工况下，在适中的Re数范围内，速度场和温度场近似呈1/7 次律指数型分布规律，图5 给出的模拟结果很好地呈现出这一特征。

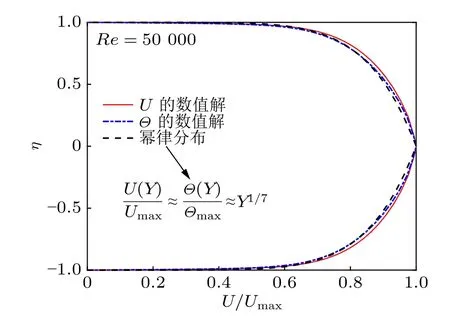
图5 管内湍流充分发展速度场和温度场模拟结果

在Re=104～106范围内，将数值计算结果与有代表性的管内充分发展湍流摩擦阻力和传热关联式[8,10]（见表2）进行对比。如图6，摩擦阻力系数的数值计算值与Filonenko 关联式计算值相当一致，两者间的相对偏差基本在 ±3%以内，而Blasius 关联式在超出其适用范围后（Re＞105）与模拟结果相差较大。传热Nu数的数值计算结果如图7 所示。图7(a)表明：对于常规流体介质（Pr＞0.5），均匀热流和均匀壁温条件下的模拟结果十分接近，均与Gnielinski 关联式吻合较好；这说明当流体Pr数较大时，传热热阻乃至温度变化主要集中在近壁处的黏性底层中，这两种边界条件对湍流传热的影响可以忽略。图7(b)表明：对于低Pr数流体（通常为液态金属），其较强的热扩散能力使得热阻分布在整个流动截面上，从而导致这两种边界条件下传热能力之间的差别不能忽视，均匀热流条件的传热能力高于均匀壁温条件（与层流工况类似）；Gnielinski 关联式的预测值明显偏低，两种边界条件下的数值计算结果与相应条件的Sleicher 关联式基本吻合。计算结果表明，本文的数值模型在不同工况条件下均能取得比较精确的模拟结果。

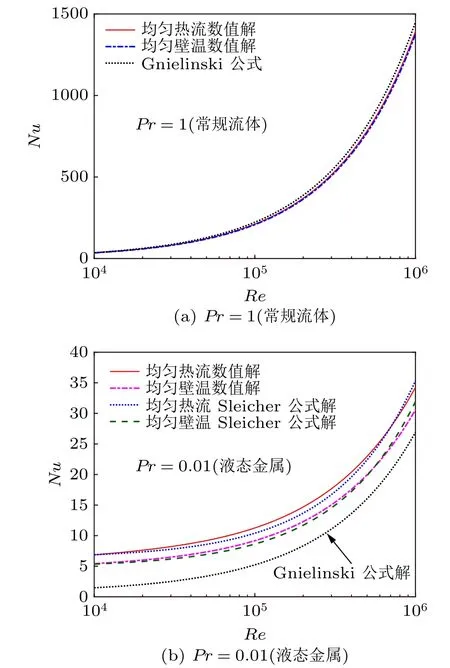
图7 管内湍流充分发展Nu 数计算结果

综上所述，基于边界层积分法，对管内充分发展流动与传热进行数学建模、程序设计和数值模拟。在过去的3 年里，笔者先后指导2017，2018 和2019 级3 名能动专业本科生围绕该算例完成了毕业设计，基本步骤是：（1）对管内不可压缩流体充分发展层流对流传热的解析解进行理论推导，熟悉控制方程组；（2）基于边界层积分法，引入无量纲变量，导出管内流动与传热的无量纲控制方程组；（3）对计算区域和控制方程组进行离散；（4）分别对层流和湍流工况、均匀热流和均匀壁温条件下的管内流动与传热进行程序设计和数值模拟；（5）改进数学模型，将数值方法从不可压缩流体推广至超临界压力流体。经过3 轮毕业设计，数值方法和计算程序不断得到完善，计算内容也不断深入，这3 名同学的工作均获得了河海大学优秀毕业设计论文。在2024 年《热工计算与程序设计》课程教学中，我们将系统地讲授这部分内容。同时，课题组不断完善课程自编讲义，为提升教学质量、编写出版教材奠定基础。

4 结论

本文将边界层积分方法与数值计算方法结合起来，通过编写计算程序，对管内充分发展流动与传热进行了数值模拟。控制方程组概念清晰、形式简洁、易于理解。数值计算方法主要由数值积分和迭代法构成，易于掌握；数值计算结果与解析解和相关经典公式进行比较，证明了该数值方法的可靠性、准确性和快速收敛性。通过该算例的实践练习，可以帮助学生巩固所学知识，锻炼学生在热工流体领域的自主编程能力、数据处理能力以及理论联系实际的能力。本文的工作将边界层理论、对流传热理论、湍流工程计算及MATLAB 程序设计、数值计算和图像绘制结合在一起，为本科阶段开展计算流体力学或数值传热学的入门教学提供了一种新的思路。