欧拉-伯努利直梁弯曲振动内力解的一种新形式1)

郝志伟 刘荣刚 陈再现

(哈尔滨工业大学海洋工程学院，山东威海 264209)

振动力学中关于弹性体弯曲振动问题求解多数教材都使用了求欧拉-伯努利直梁横向弯曲振动响应的例子，求解基本过程为先基于达朗贝尔原理建立梁的弯曲振动微分方程，再利用分离变量法求出梁的固有频率和固有模态函数，最后利用受迫振动模态叠加法给出了梁的位移响应[1-4]。得到位移响应后可分别利用梁的挠曲线近似微分方程和梁弯曲内力的微分关系就可以求出弯曲振动梁任意截面上的弯矩和剪力。

当前基础力学课程安排都是先学习理论力学，其中包括处理动力学问题的达朗贝尔原理[5-6]，再学习材料力学以及其他力学课程。计算弯曲内力是工程力学和材料力学课程的重要内容[7-9]。学生学完理论力学、材料力学后遇到杆件在动载荷作用下的强度、刚度问题时，自然的想法是应用达朗贝尔原理将动力学问题视为静力学问题求解内力而后进行强度、刚度分析。本文以振动力学中常用的欧拉-伯努利直梁受简谐载荷作用下弯曲振动为例，在得到振动响应后，直接利用梁的挠曲线近似微分方程和梁弯曲内力的微分关系计算了弯曲动内力，另外还采用达朗贝尔原理列平衡方程的方法给出了弯曲动内力。两种方法给出的弯曲动内力在形式上不完全一致，相比前者，后者给出了梁弯曲振动内力解的一种新形式，该形式的解由两部分组成，一部分是简谐力直接引起的内力，在集中力作用处剪力突变、弯矩是折点的规律与静平衡时弯曲内力的特征一致，另一部分是惯性力引起的内力，该特征有助于学生理解动载荷下梁的弯曲内力以及惯性力的作用。本文基于傅里叶级数严格证明了两种方法给出的解完全等价，并且给出了两种解形式不同的原因。欧拉-伯努利直梁受简谐载荷作用解得振动响应后，虽然再次采用达朗贝尔原理求解内力显得有些繁琐，但是该过程直观显示了达朗贝尔原理在解决动载荷作用下的杆件的强度与刚度问题上的优势，并将所学过傅里叶级数、静力学、达朗贝尔原理和梁弯曲理论揉在一起，紧密串联学生学过的重要知识，可提升基础力学教学效果。

1 简谐力作用下的欧拉-伯努利简支梁弯曲振动响应及内力

简谐力作用下的欧拉-伯努利简支梁如图1 所示，梁长为l，简谐力Psin(ωt)作用在距梁左端b处。根据受迫振动模态叠加法[1-4]，其位移稳态响应（挠曲线方程）为

图1 简谐力作用下欧拉-伯努利简支梁示意图

再分别根据梁的挠曲线近似微分方程和梁弯曲内力的微分关系[7-9]，距离梁左端x处的横截面上的弯矩和剪力分别为

考虑到梁的质量m=ρAl及ωj的表达式，剪力和弯矩可写为如下形式，并将此方法得到的剪力和弯矩分别记为 [FS]1和 [M]1。

2 达朗贝尔原理求解欧拉-伯努利直梁弯曲振动内力

由式（1）知，距离梁左端x处的加速度为

那么，如图2 所示，距离梁左端x处微段dx的惯性力 dG(x)为

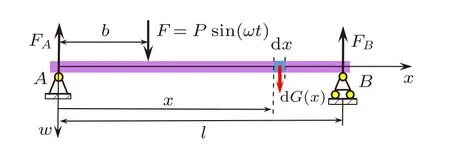
图2 简谐力作用下欧拉-伯努利简支梁受力图

梁惯性力对B点的力矩为

取梁整体为研究对象，其受力图如图2 所示，列平衡方程

解得梁左端约束力为

再取梁上左端A至x段为研究对象，其受力图如图3 所示，列平衡方程可得距离梁左端x处的横截面上的剪力和弯矩如下，并分别记利用达朗贝尔原理求得的剪力和弯矩为 [FS]2和[M]2

图3 梁左端A 到x 段分离体受力图

可以看出，剪力方程式（4），式（5）和弯矩方程式（6），式（7）均显示：第一项是简谐力直接引起的内力，在集中力作用处剪力突变、弯矩是折点的规律与静平衡时弯曲内力的特征一致，第二项是惯性力引起的内力。该特征有助于学生理解梁从静平衡到动载荷作用下的弯曲内力的不同以及惯性力的作用，而这在式（2）和式（3）中没有体现。同时，再次利用达朗贝尔原理求得的剪力方程式（4），式（5）和弯矩方程式（6），式（7）与利用梁的挠曲线近似微分方程及梁弯曲内力的微分关系求得的剪力方程式（2）和弯矩方程式（3）形式上不完全一致，这是因为梁的挠曲线近似微分方程本质上是利用本构关系给出了弯矩与弯曲变形的关系，而再次利用达朗贝尔原理求得的弯矩方程完全是通过列平衡方程的思想求得，二者有一定的区别。

下面的工作就是严格证明剪力方程式（4），式（5）和式（2）完全等价，弯矩方程式（6），式（7）和式（3）完全等价。

3 二者等价的数学证明

两种方法给出的剪力方程式（2）与剪力方程式（4）和式（5）作差，得

若下面的式（9）成立，则式（8）等于零，也即两种方法计算的剪力完全等价。

下面利用傅里叶级数证明式（9）成立。假设f(x)是 [-l,l] 上周期为 2l的偶函数

则其傅里叶级数可写为

其中

进一步计算系数cj，得

将式（12）代入式（10）得

将式（13）中常数项移到等式的一边，即可知式（9）在 [0,b)上成立。

同理，再假设f(x)是 [-l,l] 上周期为 2l的偶函数

由式（10）计算出其傅里叶级数的系数cj

于是可知

将式（15）中常数项移到等式的一边，即可知式（9）在 (b,l] 上成立，所以式（9）成立。证毕。

两种方法给出的弯矩方程式（3）与弯矩方程式（6）和式（7）作差，得

下面证明式（16）等于零，也即两种方法计算的弯矩完全等价。式（8）已被证明等于零，式（8）左右两边对x进行积分，由弯矩与剪力的微分关系知，两种方法给出的弯矩方程式的差为

其中c1，c2，c3和c4为积分常数。由于简支梁两端不能承受弯矩，也即简支梁两端横截面上弯矩为零，这与弯矩方程式（6），式（7）和式（3）给出的两种方法计算的弯矩在x=0 和x=l处的弯矩等于零是一致的，也即

于是可知

将式（19）代入式（17）即可知式（16）等于零。证毕。

4 结论

针对振动力学中常用的欧拉-伯努利直梁弯曲振动内力求解，不同于教材中利用梁的挠曲线近似微分方程和梁弯曲剪力与弯矩间的微分关系给出剪力与弯矩，本文在求出弯曲振动响应后继续利用达朗贝尔原理求弯曲振动内力，给出了一种新形式的弯曲内力，并证明了二者完全等价。虽然所给方法不一定简单，但是特征明显，新形式的弯曲内力方程直观显示了简谐力和惯性力对内力的贡献。该思路将数学中的傅里叶级数、基础力学中的静力学理论、达朗贝尔原理和梁弯曲理论自然地揉和在一起，可提升学生应用学过的数学知识和力学知识解决实际问题的能力。