考虑材料参数空间变异性的SBFEM 开裂模拟1)

林安邦 江守燕 孙立国 杜成斌

(河海大学力学与材料学院，南京 211100)

工程结构在各种内外部因素共同作用下，极易出现开裂破坏。自20 世纪初Griffith[1]的开创性工作以来，科研工作者们对固体材料的破坏机理进行了大量研究。

尽管如此，对固体材料中裂纹的萌生和扩展的模拟研究仍然是一项具有挑战性的工作。Miehe等[2]通过引入经典损伤力学中的历史最大损伤能释放率等概念，将脆性断裂相场模型应用于固体结构的破坏分析。Wu[3]提出了分析固体结构损伤破坏问题的一类统一相场理论框架。为了解决网格敏感性问题，非局部模型[4]逐渐发展了起来。受近场动力学[5]和统一相场理论的启发，卢广达等[6]提出了一类非局部宏-微观损伤模型，该模型引入近场动力学中物质点和物质点偶的概念，很好地避免了网格敏感性问题。

比例边界有限元法（scaled boundary finite element methods，SBFEM）是Song 和Wolf 提出的一种新型半解析数值计算方法[7]，该方法在径向上有解析解，在环向上有数值解，且能够降低一维计算维度。SBFEM 与四叉树网格的结合实现了网格的全自动剖分，剖分效率极高，且粗细网格过渡非常方便。SBFEM 已成功运用于解决非局部损伤问题[8]，杜成斌等[9]将SBFEM 与非局部宏-微观损伤模型相结合进行结构损伤模拟取得了较好的效果。在实际工程问题中，裂纹往往呈现出蜿蜒曲折的形态，实验所得曲线也往往在一定范围内波动，这是因为材料本身内禀具有随机性，这就使得采用固定参数进行数值模拟时，很难精确预测材料的力学响应。因此，在研究中考虑材料参数的空间变异性是十分必要的[10]。

本工作通过考虑材料细观物理参数的空间变异性和材料任意两点间存在的自相关性，采用基于乔列斯基分解的中点法模拟相关随机场。基于SBFEM 框架的非局部宏微观损伤模型结合若干数值算例，探讨材料参数的空间变异性对结构损伤产生和发展的影响，以及结构损伤发展的随机性与结构的受力情况和自身缺陷之间的关系。

1 相关随机场模拟方法

1.1 自相关函数

材料参数的空间变异性分析需要考虑随机场计算区域内任意两个不同空间位置处材料参数的相关性，引入自相关函数描述这一特性。任意位置Qi处参数的取值Hi(xi,yi)和Qj处的取值Hj(xj,yj)间的自相关性系数定义为

式中，COV(·)和V ar(·)分别为协方差和方差函数。Qi=(xi,yi)和Qj=(xj,yj)分别为随机场第i个单元和第j个单元的比例中心坐标，其中i,j=1,2,...,ne，这里ne为单元数目。由于实际问题很难获取到材料参数的随机分布数据，一般采用理论自相关函数描述材料参数的空间自相关性。文中采用指数型自相关函数

式中，τx和τy分别为空间任意两点间的水平和垂直方向相对距离，δh和δv分别为水平和垂直方向的自相关长度。

1.2 相关随机场的模拟

由理论自相关函数可直接计算出材料参数原始空间中的自相关系数

式中，χ={χi=H(xi,yi)}为计算域内任一点i处参数的取值，是一维度为ne×ne的空间自相关系数矩阵。

文中采用拉丁超立方样本构成标准正态随机样本矩阵Γ；再对自相关系数矩阵进行乔列斯基分解，即

式中，L为下三角矩阵。于是，得到参数m的相关标准高斯随机场为

对该随机场取指数可以得到参数m的相关对数正态随机场

式中，Π为维度与(x,y)相同元素全为1 的矩阵，σm和µm分别为对数正态变量m的均值和标准差，σlnm和µlnm分别为对应的正态变量lnm的均值和标准差。

2 基于SBFEM 的非局部宏微观损伤模型

非局部宏微观损伤模型结合了近场动力学中物质点对的思想和统一相场理论中能量退化函数的概念，并将其纳入到连续介质损伤力学框架中。

2.1 细微观损伤与拓扑损伤

假设二维空间内存在一连续体域Ω，x=(x1,x2)和为Ω（中的）两个物质点。x与x′组成的物质点对记为x,x′，ξ=x-x′为两物质点的空间差，‖ξ‖为相应的距离，连续体发生变形后，u=u(x)和u′=u′(x′)分别为物质点x和x′的位移，根据图1 所示，定义物质点对之间的变形为

图1 物质点对变形几何Fig.1 Deformation of material point pair

式中，ν=ξ/‖ξ ‖为物质点对的单位方向向量。由此定义物质点对的伸长量为

式中，H(·)为Heaviside 阶跃函数，当λ≤0 时，H(λ)=0，否则H(λ)=1 。

即物质键变形历史的最大超越伸长量。

为了表征物质键的损伤程度，定义一个细微观损伤函数ω(x,x′,t)，并将其进行归一化，即ω ∈[0,1] 。它是历史最大超越伸长量κ的单调非减函数，取为

式中，γ ＞0 为模型参数，γ越大，损伤的发展速度越快。由于Heaviside 阶跃函数能够表征不连续性，因此，细微观损伤刻画了固体在物质键层次的不连续程度。定义物质点x的影响域半径为ℓ，Dℓ(x)为物质点x的影响域。

宏观损伤是由细微观损伤的累积造成的，引入拓扑损伤来表征宏观损伤程度，为了表明宏观损伤的产生和发展是非局部化的，将其定义为

式中，权函数φ(x,x′)应满足非负性、定域性及归一性的要求，取权函数为

式中，vol(·)表示体积测度。

宏微观损伤模型将结构的损伤情况同物质点偶的破坏联系起来，以物质点对之间的变形λ是否超过临界伸长量来确认损伤情况，且与材料弹性模量、抗压强度等参数相关，因此有必要考虑临界伸长量的参数空间变异性。

2.2 能量退化函数

连续体的损伤发展必然伴随着能量的耗散，引入能量退化因子g，g为拓扑损伤的函数，记作能量退化函数g=g(Θ)。g(Θ)应满足g(0)=1,g(1)=0 。由于损伤总是耗能的，则dg(Θ)/dQ≤0。能量退化函数g(Θ)是区间 [0,1] 上的凸函数。非局部宏微观损伤模型中的能量退化函数采用两参数的有理分式，其形式为

式中，p和q均为退化参数，由材料自身性质决定。

2.3 非局部损伤模型在SBFEM 中的实现

在连续介质力学中，应力应变的本构关系为

式中，σ为应力张量，ε为应变张量，D为弹性矩阵。在非局部宏微观损伤模型中，通过能量退化函数g=g(Θ)的引入，建立起拓扑损伤与应力应变之间的联系，则本构关系转变为

式中，DD=gD为弹性损伤矩阵。

弹性静力学问题的SBFEM 方程为[7]

该方程是关于ξ的二阶齐次微分方程，E0，E1和E2是与材料参数和形状有关的系数矩阵，子域在损伤状态下的系数矩阵为

式中，ξ为径向坐标，η为环向坐标，|J| 为雅克比矩阵行列式，B1(η)和B2(η)为应变-位移转换矩阵，对式（16）进行求解并将式（17）代入，即可得到子域在损伤状态下的刚度矩阵（刚度矩阵的具体求解方法参见文献[9]）。将所有的子域刚度矩阵进行组装，得到损伤状态下的离散方程为

式中，KD为损伤状态下的整体刚度矩阵，U为整体节点位移向量，F为整体载荷列阵。

3 数值算例

3.1 预制缺口三点弯梁准静态开裂模拟

预制缺口三点弯梁的几何尺寸、边界条件、加载方式如图2(a)所示。按平面应力问题处理。运用四叉树法对其进行网格划分，并对裂纹可能产生和发展的区域进行加密处理（图2(b)），确保损伤区域内的网格尺寸小于ℓ/5，避免出现网格敏感性问题。四叉树网格及加密区域如图2(b)所示，单元数为3530，结点数为3747。

材料的弹性模量E=20 GPa，泊松比ν=0.2。依据文献[9]给出的非局部宏微观损伤模型参数，取影响半径ℓ=5 mm，γ=1 000，p=3，q=4 。考虑临界伸长量的空间变异性，均值=1.125 µm，变异系数=10%，自相关长度δh=5 mm，δv=5 mm，生成5 个临界伸长量随机场样本。

图3 为不同随机场样本计算得到的载荷-加载点位移曲线，图4 为部分样本的裂纹形态及参数均匀分布结果。如图3 所示，将临界伸长量作为随机场计算得到的载荷-位移曲线的变化范围基本在实验结果[11]范围之内，与不考虑参数随机性的宏微观模型[9]所得曲线走向也基本一致，与统一相场模型[12]所得曲线在下降段有所差别。这表明，在考虑参数的空间变异性后，采用宏-微观损伤模型模拟材料的受力和损伤过程是合理的，且可以体现出材料内禀的随机性。考虑参数随机性计算出部分最终裂纹形态如图4 所示，不难看出，裂纹形态各不相同，考虑参数随机性的最终裂纹形态是略有曲折的，不考虑参数随机性的裂纹形态是笔直向上的。考虑参数空间变异性的宏-微观损伤模型能很好地模拟出裂纹产生和发展的过程，结果更加合理。

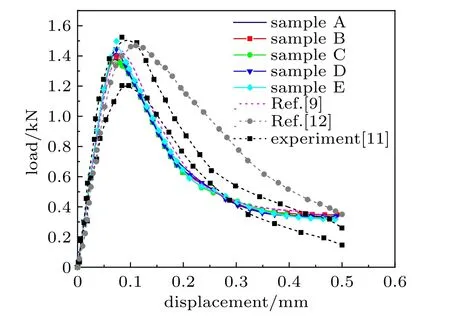
图3 预制缺口三点弯梁载荷-加载点位移曲线Fig.3 Load-displacement curve of notched three-point bending beam

图4 三点弯梁各样本最终裂纹形态Fig.4 Final cracking modes of three-point bending beam with different samples

3.2 预制缺口剪切梁开裂模拟

图5 为一剪切梁，其几何尺寸、边界条件和加载方式及网格划分如图所示。该剪切梁为有机玻璃材质，因为其具有强非线性回弹特性，能很好地检验数值模型的优良性。分析中试件按平面应力问题考虑，同样采用四叉树对其进行网格划分，单元数为9744，结点数为10 032。

图5 预制缺口剪切梁及其网格划分Fig.5 Notched shear beam and the mesh

材料参数：弹性模量E=3.102 GPa，泊松比ν=0.35 。宏-微观损伤模型参数：影响半径ℓ=4 mm，γ=200 000，p=4，q=4 。考虑临界伸长量的空间变异性，均值=0.018 mm，变异系数=10%，自相关长度δh=4 mm，δv=4 mm，生成5 个临界伸长量随机场样本。

五个随机场样本计算得到的载荷-裂纹口张开位移（crack mouth pening displacement，CMOD）曲线和载荷-加载点位移曲线如图6 所示，部分样本及参数均匀分布的裂纹最终形态如图7 所示。

图6 剪切梁不同随机场得到的载荷-位移曲线Fig.6 Load-displacement curves for different samples

图7 剪切梁各样本最终裂纹形态Fig.7 Final cracking modes of shear beam with different samples

图7 将各样本计算得到的载荷-CMOD 曲线、载荷-加载点位移曲线与实验所得曲线[13]、基于有限元法的宏微观损伤模型[6]和基于混合元的各向同性损伤模型[14]模拟结果进行了对比。如图6(a)所示，各样本的载荷-CMOD 曲线与实验结果和其他数值模拟结果的曲线基本吻合；图6(b)给出的载荷-加载点位移曲线与实验结果对比虽然略有差异，但施加的载荷最大值基本一致，总体走向也基本相同，且表现出了该结构的强非线性回弹特质，这是一般的数值模拟方法很难捕捉到的。

图7 给出了其中3 个样本计算出的裂纹最终形态，并与未考虑参数空间变异性的数值模拟结果做了对比。可以发现，未考虑参数变异性时，文献[14-15]和论文方法模拟出来的裂纹形态是一条光滑的曲线，考虑参数空间变异性后，各样本计算出的裂纹最终形态是曲折的，这更符合实际工程情况。由于受力情况相对于三点弯梁更加复杂，各样本的裂纹最终形态表现出更强的变异性。这表明在复杂的受力情况下，裂纹产生和发展的过程随机性更大。

3.3 预制圆孔剪切梁开裂模拟

为了进一步探究参数的空间变异性对复杂工况下结构开裂过程的影响，考虑剪切梁含圆孔缺陷的情况。试件的几何尺寸、边界条件及加载方式和网格划分如图8 所示。对圆孔缺陷部分及裂纹可能萌发和发展的区域进行网格加密处理，单元数为8285，结点数为8741，同样取变异系数=10%，自相关长度取值不变，生成5 个随机场。

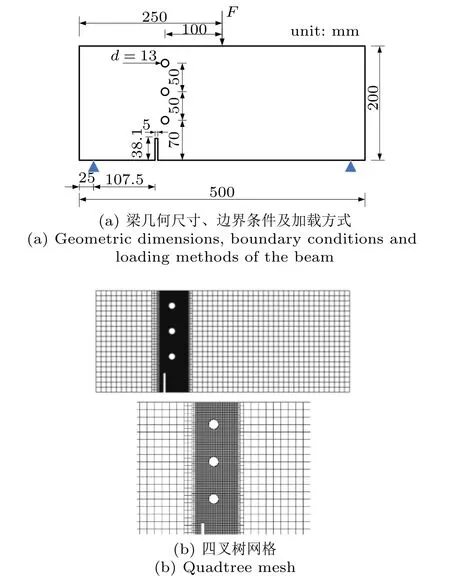
图8 含圆孔缺陷剪切梁及其网格Fig.8 Shear beam with circular flaws and the mesh

5 个随机场样本计算得到的载荷-CMOD 曲线如图9 所示，裂纹最终形态如图10 所示。在图9(b)中，各样本的载荷-加载点位移曲线依然表现出了强非线性回弹特质。

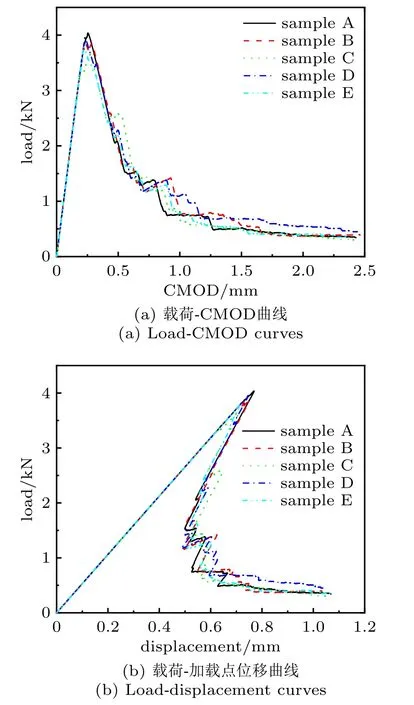
图9 含缺陷剪切梁不同随机场得到的载荷-位移曲线Fig.9 Load-deformation curves for different samples

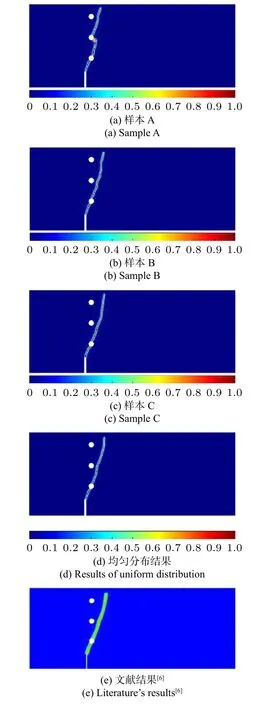
图10 含缺陷剪切梁各样本最终裂纹形态Fig.10 Final cracking modes of shear beam with flaws under different samples

图10 给出了其中3 个样本计算出的最终裂纹形态及文献和运用论文方法未考虑参数空间变异性的模拟结果。未考虑变异性及文献[6]的结果中的裂纹走向一致，均从缺口尖端开始萌发向右上方发展，穿过第一个圆孔缺陷后有向第二个圆孔缺陷发展的趋势但最终未被俘获继续向右上方发展。考虑参数空间变异性后，各样本计算出的裂纹走向具有随机性。值得注意的是，样本A 的计算结果中，裂纹在穿过第一个圆孔缺陷后，又被第二个圆孔缺陷俘获，并穿过第二个圆孔继续向右上方发展。在变异系数不变，考虑圆孔缺陷的情况下，裂纹最终形态的变异性更强。这表明在原试件有缺陷的情况下，考虑参数的空间变异性后，裂纹的产生和发展的随机性更大，因此，对于复杂的结构，在数值模拟的过程中考虑参数的空间变异性，分析裂纹发展的多种可能性是十分必要的。

4 随机场参数的影响研究

4.1 自相关长度的影响

本节主要探究随机场的自相关长度对计算结果的影响。在变异系数=10% 不变的情况下，分别取自相关长度δh=δv=ℓ/10，ℓ，10ℓ3 种不同的情况，每种情况均生成5 个随机场样本，计算得到的载荷-位移曲线如图11 所示，从图中可以看出，载荷-位移曲线的变异性随着自相关长度增大而增大，当自相关长度取ℓ/10 时，曲线的极值基本一致，曲线的变异性几乎可以忽略不计。自相关长度取ℓ时，曲线极值出现了明显的波动，曲线变异性升高；当自相关长度取 10ℓ时，曲线的变异性进一步升高。实际上，由于非局部损伤模型中定义的损伤是一个加权求和，是一种均值，随着随机场的自相关长度逐渐增大，影响域内各物质点偶的临界伸长量的自相关性越强，数值大小会整体偏大或偏小，各影响域内变量均值的方差也会越来越大，导致曲线的变异性增强。

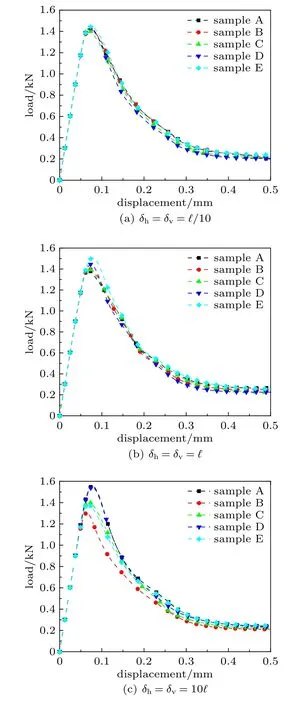
图11 不同自相关长度得到的载荷-位移曲线Fig.11 Load-deformation curves with different autocorrelation length

4.2 变异系数的影响

随机场变异系数也是影响计算结果的重要因素，本节主要探究变异系数和自相关长度对计算结果的影响规律。变异系数分别取20%和30%，随机场不同自相关长度得到的载荷-位移曲线如图12 所示。从图中可以看出，随着变异系数的增大，无论自相关长度取值如何变化，曲线的变异性都在增强。当自相关长度取值较小时，随着变异系数的增大，曲线极值的波动范围略有变大；随着自相关长度的增大，曲线极值波动范围的增加幅度较明显。在变异系数取30%，自相关长度取 10ℓ时，极值的波动范围已经大大超出了试验范围。由此可见，随着随机场的自相关长度的增大，随机场变异系数对计算结果的影响也显著增强。这是由于非局部模型对损伤的定义类似于均值的特性，在随机场自相关长度较小时，即使变异系数增加，各影响域内参数均值的差距也很小，随着自相关长度的增加，甚至超过影响域半径时，变异系数的增加会使各影响域内参数均值之间的差距增大，从而导致曲线变异性的增大。

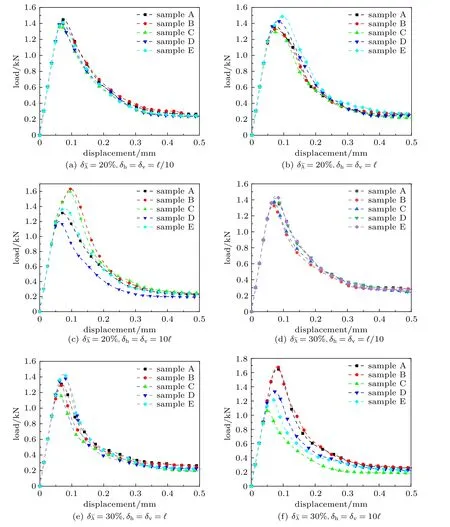
图12 不同变异系数得到的载荷-位移曲线Fig.12 Load-deformation curves for different coefficients of variation

5 结论

建立了SBFEM 框架下的宏-微观损伤模型，考虑材料细观物理参数的空间变异性和材料任意两点间存在的自相关性，探讨了材料参数的空间变异性对结构开裂过程的影响，得出以下几点结论。

（1）基于SBFEM 的宏-微观损伤模型分析结构开裂问题时，不需要人为预设裂纹的开裂路径，可以自动地预测裂纹的开裂模式。

（2）针对结构材料存在的内在随机性，裂纹扩展路径具有不确定性，因此，考虑材料参数的空间变异性对裂纹扩展路径的影响至关重要。结构的受力情况和结构本身是否存在缺陷对裂纹扩展的随机性有较大的影响，受力情况越复杂，结构内部缺陷越多，裂纹发展模式越是复杂多变，这与实际情况是相符的，也反映出数值模拟在处理固体结构破坏问题时考虑参数空间变异性的必要性。

（3）自相关长度和参数变异系数对结构开裂分析结果有重要影响。随着自相关长度的增大，结果的变异性增强；同时，自相关长度的取值也一定程度上决定变异系数对计算结果的影响程度，自相关长度越大，变异系数对计算结果的影响程度越大，因此，随机场模型自相关长度的取值至关重要，可与非局部模型中影响域取值相当。